Las causas del movimiento de los cuerpos son las interacciones de unos cuerpos con otros. Estas interacciones pueden ser por contacto o a distancia.

• Por contacto: Golpeamos una pelota con una pala en un frontón, empujamos el carro de la compra o tiramos de una maleta.
• A distancia: Dejamos caer un objeto desde cierta altura, un cometa se mueve alrededor del Sol, se pone un imán cerca de otro imán.

Partícula aislada. Ley de inercia

Si sobre un cuerpo no actúa fuerza alguna, su velocidad no cambia ni en magnitud ni en dirección.

Un cuerpo desliza en una pista horizontal. Su velocidad disminuye hasta que se detiene al cabo de un cierto tiempo. Si la pista es de hielo, o el cuerpo se mueve sobre un carril de aire, el bloque desliza sin apenas rozamiento hasta que se detiene después de un tiempo mucho mayor. Podríamos imaginar una pista horizontal ideal sobre la que un cuerpo se mueva con velocidad constante.

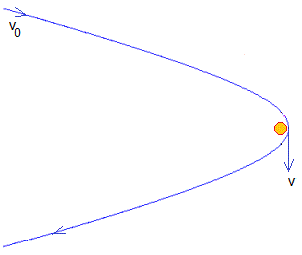
Un cometa sigue una trayectoria casi rectilínea hasta las proximidades del Sol donde cambia tanto el módulo como la dirección de la velocidad, tal como se muestra en la figura

Una partícula libre o aislada se mueve con $\overrightarrow{v}=\text{cte}$

Se define momento lineal como una magnitud vectorial, igual al producto de la masa por la velocidad $\overrightarrow{p}=m\overrightarrow{v}$

Sistema aislado formado por dos partículas. Segunda y tercera ley de Newton

Consideremos un sistema aislado formado por dos partículas de masas m₁ y m₂, que interactúan entre sí, como la Tierra y la Luna.

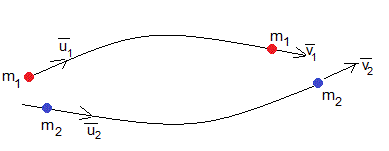
Calculamos el momento lineal total del sistema en el instante t y en el instante t'

${\displaystyle \begin{array}{l}t\to \overrightarrow{p}=\overrightarrow{p_1}+\overrightarrow{p_2}=m_1\overrightarrow{u_1}+m_2\overrightarrow{u_2}\hfill \\ t\text{'}\to \overrightarrow{p}={\overrightarrow{p\text{'}}}_1+{\overrightarrow{p\text{'}}}_2=m_1\overrightarrow{v_1}+m_2\overrightarrow{v_2}\hfill \end{array}}$

Dado que es un sistema aislado, el momento lineal total del sistema no ha cambiado

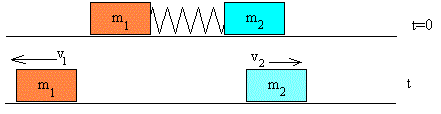
Consideremos un sistema aislado formado por dos carritos de masas m₁ y m₂. En medio hay un dispositivo de disparo consistente en un muelle elástico comprimido. En la situación inicial, el momento lineal total es cero. Después, el momento lineal total sigue siendo cero.

${\displaystyle \begin{array}{l}{m}_1\overrightarrow{v_1}+m_2\overrightarrow{v_2}=0\hfill \\ m_1\overrightarrow{v_1}=-m_2\overrightarrow{v_2}\hfill \end{array}}$

Las velocidades de los carritos v₁ y v₂ después del disparo, tendrán la misma dirección pero sentidos contarios. Si m₁>m₂ entonces el módulo de v₁<v₂.

La constancia del momento lineal total, implica que en un sistema aislado formado por dos partículas, el cambio en el momento lineal de la partícula de masa m₁ es igual y de sentido contrario al cambio de momento lineal de la partícula de masa m₂.

${\displaystyle {\overrightarrow{p\text{'}}}_1-\overrightarrow{p_1}=-(\overrightarrow{p}{\text{'}}_2-\overrightarrow{p_2})}$

Estos cambios tienen lugar en un intervalo de tiempo Δt=t'-t. Los cocientes son también iguales y de sentido contrario

${\displaystyle \frac{\overrightarrow{\Delta p_1}}{\Delta t}=-\frac{\overrightarrow{\Delta p_2}}{\Delta t}}$

En el límite cuando Δt→0 también se cumple

${\displaystyle \begin{array}{l}\underset{\Delta t\to 0}{\lim }\left(\frac{\overrightarrow{\Delta p_1}}{\Delta t}\right)=-\underset{\Delta t\to 0}{\lim }\left(\frac{\overrightarrow{\Delta p_2}}{\Delta t}\right)\hfill \\ \frac{d\overrightarrow{p_1}}{dt}=-\frac{d\overrightarrow{p_2}}{dt}\hfill \end{array}}$

Segunda ley de Newton. Definición de fuerza

Se define fuerza, como una magnitud vectorial

${\displaystyle \overrightarrow{F}=\frac{d\overrightarrow{p}}{dt}}$

Cuando la masa m de la partícula es constante, la definición de fuerza se escribe

${\displaystyle \begin{array}{l}\overrightarrow{F}=m\frac{d\overrightarrow{v}}{dt}\\ \overrightarrow{F}=m\overrightarrow{a}\end{array}}$

Tercera ley de Newton. Principio de acción y reacción

La conservación del momento lineal en un sistema aislado de dos partículas interactuantes, nos lleva a

${\displaystyle {\overrightarrow{F}}_1=-{\overrightarrow{F}}_2}$

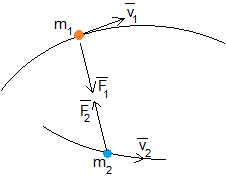
La interacción de la partícula 2 con la 1 se describe en términos de la magnitud vectorial $\overrightarrow{F_1}$ , (fuerza que ejerce la partícula 2 sobre la 1) que hace que la partícula de masa m₁ cambie su velocidad $\overrightarrow{v_1}$ tanto en módulo como en dirección

La interacción de la partícula 1 con la 2 se describe en términos de la magnitud vectorial $\overrightarrow{F_2}$ , (fuerza que ejerce la partícula 1 sobre la 2) que hace que la partícula de masa m₂ cambie su velocidad $\overrightarrow{v_2}$ tanto en módulo como en dirección

La tercera ley de Newton nos dice que ambas fuerzas son iguales y de sentido contrario. $\overrightarrow{F_1}=-\overrightarrow{F_2}$

Principio de superposición

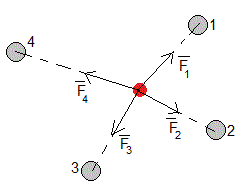
Cuando un cuerpo de masa m (en color rojo) está sometido a la influencia de las interacciones de otros cuerpos, cada interacción de un cuerpo de color gris con el cuerpo de color rojo, se describe mediante una fuerza $\overrightarrow{F_i}$ La resultante (suma vectorial) de las fuerzas es igual a la masa del cuerpo por la aceleración

${\displaystyle m\overrightarrow{a}=\overrightarrow{F_1}+\overrightarrow{F_2}+\overrightarrow{F_3}\mathrm{...}+\overrightarrow{F_n}}$

Cuando la resultante de las fuerzas que actúan sobre un cuerpo es cero, se dice que están en equilibrio

Composición y descomposición de fuerzas

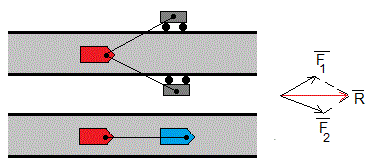
Supongamos un barco que navega por el canal de Panamá arrastrado por dos locomotoras que circulan por vías paralelas a ambos orillas del canal, tal como se muestra en la figura.

La interacción de la locomotora con el barco se describe mediante una fuerza que tiene la dirección del cable que une la locomotora y el barco y sentido hacia la locomotora. La acción de ambas locomotoras es equivalente a la de un remolcador que tire del barco con una fuerza $\overrightarrow{R}$ , que es la suma vectorial de $\overrightarrow{F_1}$ y $\overrightarrow{F_2}$.

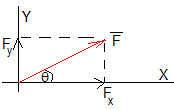
La acción de la fuerza $\overrightarrow{F}$ es equivalente a la acción simultánea de sus componentes rectangulares F_x y F_y

F_x=F·cosθ
F_y=F·sinθ

Ejercicio

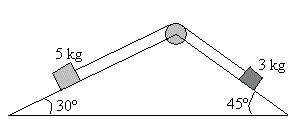
En el problema de la figura, calcular

• La aceleración del sistema
• La tensión de la cuerda.

Tómese g=10 m/s². Se supone que los cuerpos deslizan sin fricción. La polea tiene masa despreciable

Para resolver los problemas de dinámica de una partícula, se dibuja un esquema de la situación como en este dibujo, identificando el objeto o los objetos de interés.

Describimos mediante vectores fuerza, las interacciones de cada uno de los dos cuerpos con los que les rodean, que dibujamos mediante flechas, sobre dichos cuerpos. Le damos a cada flecha un nombre significativo: T para la tensión, N para la reacción del plano, F_r para la fuerza de rozamiento, etc.

• El peso es la fuerza de atracción de la Tierra sobre un cuerpo de masa m cerca de su superficie, mg

• Los cuerpos están soportados por planos inclinados. La normal o reacción del plano es una fuerza perpendicular al plano en el punto de contacto

• Los cuerpos están unidos mediante una cuerda que pasa por una polea de masa despreciable. El módulo de la fuerza es la tensión T de la cuerda, habitualmente desconocida, su dirección es a lo largo de la cuerda y su sentido, tirando del cuerpo que se trate. Las fuerzas que ejerce un cuerpo sobre el otro a través de la cuerda se indican en la figura mediante la flecha identificada por T

• Elegimos un sistema de referencia conveniente para resolver el problema. En este caso, un sistema de referencia formado por dos ejes X e Y, uno a lo largo del plano inclinado y otro perpendiculamente al plano inclinado

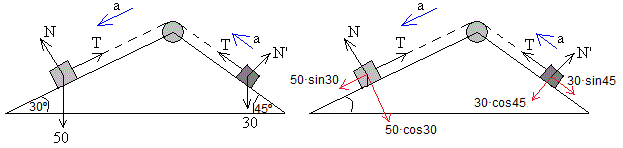
Se sustituye la fuerza peso, por la acción simultánea de sus componentes rectangulares, en la dirección de los planos inclinados y perpendicularmente a los mismos (en color rojo en la figura de la derecha)

Los cuerpos están en equilibrio en la dirección perpendicular a los planos inclinados

N=50·cos30°
N'=30·cos45°

Los cuerpos se mueven con las misma aceleración a a lo largo de los planos inclinados. Las ecuaciones del movimiento de cada uno de los cuerpos son:

50·sin30-T=5a
T-30·sin45=3a

a=0.47 m/s², T=22.6 N

Impulso

Consideremos un cuerpo de masa m que se mueve a lo largo del eje X. Sobre el cuerpo actúa una fuerza F que cambia con el tiempo t. La definición de fuerza es.

${\displaystyle \begin{array}{l}F=\frac{dp}{dt}\\ mv-m{v}_0={\displaystyle \underset{t_0}{\overset{t}{\int }}F·dt}\end{array}}$

Donde v₀ es la velocidad del móvil en el instante t₀. El área bajo la curva F, t, la integral definida, se denomina impulso.

Práctica de laboratorio

Un carrito de masa m se mueve en un carril con velocidad v₀ y choca contra un dispostivo fijo (muelle, plastilina, imán), después del choque la velocidad del carrito es v

Un sensor de movimiento mide la velocidad inicial v₀ y la velocidad final v del carrito. Cuando el carrito se aleja del sensor la velocidad es positiva y cuando se acerca, la velocidad es negativa

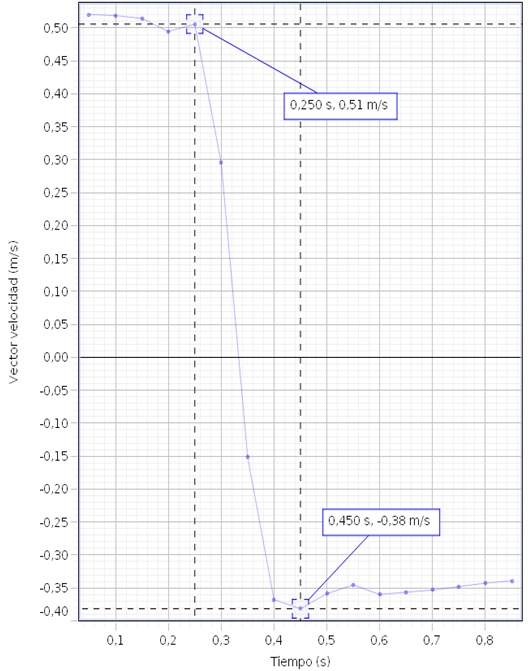
El cambio de momento lineal es mv-m(-v₀)=m(v+v₀)

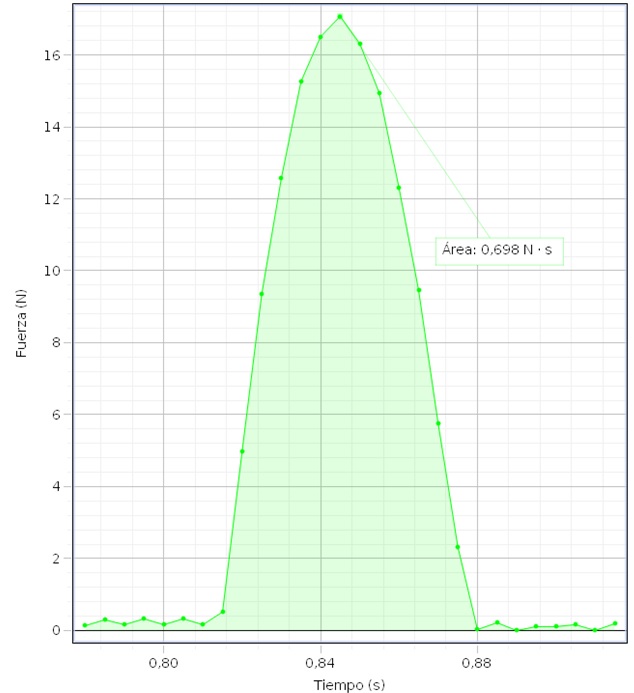
Un sensor de fuerza mide la fuerza que ejerce el dispositivo sobre el carrito, que hace que cambie el módulo y dirección de su velocidad.

Una vez registrada la fuerza en función del tiempo, la herramienta área de CAPSTONE calcula el área bajo la curva, es decir, el impulso, en color verde en la figura

Los resultados de la experiencia, realizada por un estudiante de primer curso, se recogen en la tabla:

Ejercicio

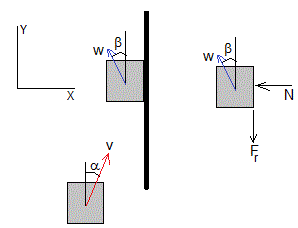
Un cubo elástico de masa m se dirige hacia una pared vertical con velocidad v en la dirección α. El coeficiente de rozamiento entre el cubo y la pared es μ.

Vamos a calcular la velocidad w y su dirección β después del choque

• El impulso de la fuerza N que ejerce la pared sobre el cubo cambia el momento lineal del cubo a lo largo del eje X

En un choque elástico, la componente v_x=v·sinα de la velocidad del cubo cambia de sentido w_x=-v·sinα

${\displaystyle \begin{array}{l}-{\displaystyle \underset{0}{\overset{t_x}{\int }}N·dt}=m\left(w_x-v_x\right)\\ -{\displaystyle \underset{0}{\overset{t_x}{\int }}N·dt}=m\left(-v\sin \alpha -v\sin \alpha \right)=-2mv\sin \alpha \end{array}}$

donde t_x es el tiempo de choque, el tiempo que está el cubo en contacto con la pared vertical

Si no hubiese rozamiento, la componente w_y=v_y=v·cosα permanecería inalterada y el ángulo β=α. Si hay rozamiento F_r=μN el ángulo β≠α, como vamos a comprobar

• El impulso de la fuerza de rozamiento F_r que ejerce la pared sobre el cubo cambia el momento lineal del cubo a lo largo del eje Y

Pueden ocurrir dos casos:

1. Que antes de que finalice el choque, t_x, la componente w_y≠0 de la velocidad del bloque no se anule

${\displaystyle \begin{array}{l}-{\displaystyle \underset{0}{\overset{t_x}{\int }}{F}_r·dt}=m\left(w_y-v_y\right)\\ -\mu {\displaystyle \underset{0}{\overset{t_x}{\int }}N·dt}=m\left(w_y-v\cos \alpha \right)\\ -2\mu v\sin \alpha =w_y-v\cos \alpha \\ w_y=v\left(\cos \alpha -2\mu \sin \alpha \right)\end{array}}$

El ángulo β es

${\displaystyle \tan \beta =\frac{w_x}{w_y}=\frac{v\sin \alpha }{v\left(\cos \alpha -2\mu \sin \alpha \right)}=\frac{\tan \alpha }{1-2\mu \tan \alpha }}$

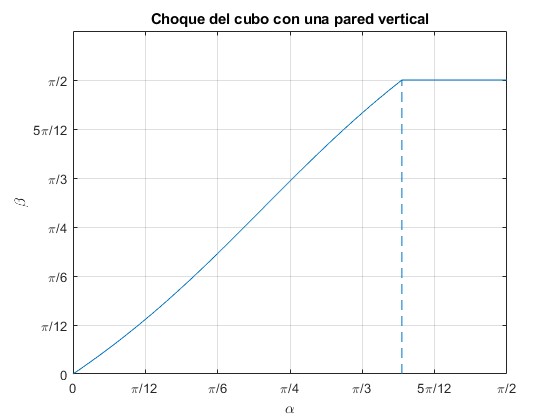
Cuando el denominador tiende a cero, (w_y no puede ser negativa), el ángulo β→π/2

2. Que antes de que finalice el choque, t_x, la componente w_y=0 de la velocidad del bloque se anule

${\displaystyle \tan \beta =\infty ,\beta =\frac{\pi }{2}}$

El cubo se mueve perpendicularmente a la pared después del choque

Resumiendo

${\displaystyle \beta =\{\begin{array}{l}\arctan \left(\frac{\tan \alpha }{1-2\mu \tan \alpha }\right),\tan \alpha <\frac{1}{2\mu }\\ \frac{\pi }{2},\tan \alpha \ge \frac{1}{2\mu }\end{array}}$

Actividades

Se introduce

• El ángulo incidente en grados, α, en el control titulado Angulo
• El coeficiente de rozamiento μ, en el control titulado Coeficiente
• Se ha fijado la velocidad v=1 antes del choque

En la parte superior iquierda, se proporcionan los datos de las componentes de la velocidad después del choque w_x y w_y, del ángulo β y del módulo de la velocidad w

Referencias

Sidney B. Cahn, Boris E. Nadgorny. A guide to physics problems, part 1. Mechanics, Relativity, and Electrodynamics.. Kluwer Academic Publishers, 2004. Problem 1.3