El reloj de arena

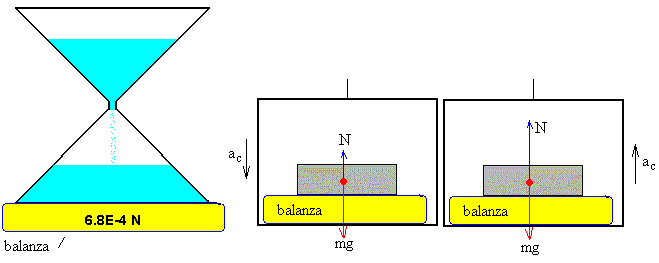
A medida que la arena fluye del recipiente superior al inferior, su centro de masas se mueve hacia abajo, su aceleración ac es hacia abajo, por lo que la resultante de las fuerzas sobre el sistema será hacia abajo y por tanto, la balanza medirá una fuerza N que será menor que el peso mg.
Este razonamiento como vamos a ver es incorrecto, ya que aunque es cierto que el centro de masas se mueve hacia abajo, su aceleración ac es hacia arriba. La balanza medirá una fuerza N que será mayor que el peso mg.
Posición, velocidad y aceleración del centro de masas
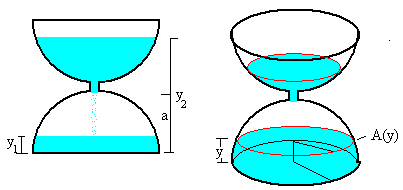
En la figura, se muestra un reloj de arena en un instante t. Sea y2 la posición de la superficie libre de la arena en la porción superior e y1 la posición en la porción inferior. La posición del cuello cilíndrico que une ambas porciones es a. Sea A(y) el área de la sección trasversal del reloj de arena en la posición y, y ρ la densidad de la arena.
La posición Yc del centro de masas del sistema está dada por
donde M es la masa total del reloj de arena, y C es una constante que tiene en cuenta la arena que está cayendo, la masa del recipiente de vidrio y otros detalles fijos de la construcción del reloj de arena.
Derivando con respecto del tiempo, obtenemos la velocidad del centro de masas vc
El flujo f se define como la masa que sale del recipiente superior en la unidad de tiempo, o que entra en el recipiente inferior en la unidad de tiempo.
La velocidad del c.m. vc tiene una expresión muy simple
Mvc=f(y1-y2)
Como y1<y2, la velocidad del c.m vc es negativa (hacia abajo)
Derivando de nuevo, con respecto del tiempo, obtenemos la aceleración del centro de masas
El flujo f de arena es aproximadamente constante, por lo que el segundo término es casi nulo.
Colocamos el reloj de arena sobre una balanza electrónica. Sea ΔF, la diferencia entre el peso N del reloj en marcha y el peso Mg del reloj de arena parado.
(1)
ΔF>0, la aceleración del c.m. es siempre positiva, hacia arriba, aunque el centro de masas se mueve hacia abajo. Cuando el reloj está en marcha, la balanza mide una fuerza N mayor que el peso Mg del reloj parado.
En esta deducción, no se considera el estado transitorio, cuando la arena comienza a caer ni cuando termina de fluir la arena, solamente la situación intermedia.
Reloj de arena de forma cilíndrica
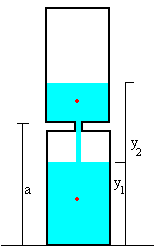
Consta de dos cilindros iguales de radio R y longitud L, unidos por un cuello por el que fluye arena a razón constante de f kg/s.
Posición del centro de masa
Calculamos el centro de masas de la arena contenida en ambos recipientes, despreciando el cuello que los une. Los centros de masas de la arena de cada una de las porciones se señalan en la figura mediante puntos de color rojo.
- La masa (o volumen para un cuerpo homogéneo) de la porción inferior es πR2y1
- La posición de su centro de masas y1/2
-
El volumen de la porción superior πR2(y2-a)
-
La posición de su centro de masas (y2+a)/2
La posición del centro de masas del sistema es
Velocidad del c.m.
Derivando con respecto del tiempo
donde se ha definido el flujo f de arena como
Aceleración del c.m.
Derivando respecto del tiempo
La aceleración del centro de masas es constante
A partir de la expresión (1) del apartado anterior obtenemos alternativamente la aceleración del c.m.
Como A(y1)=A(y2)=πR2
y la masa de la arena es M=ρ πR2L
Reloj de arena de forma cónica
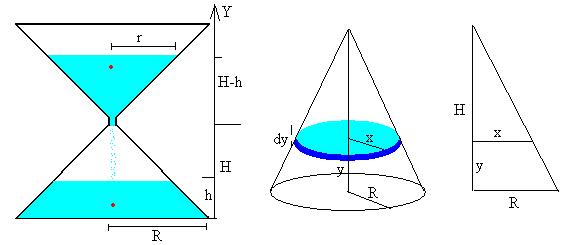
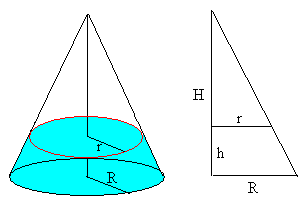
Consta de dos conos iguales de radio R y altura H, unidos por sus vértices.
Posición del centro de masa
En el instante t, la arena está contenida en un cono de radio r y altura (H-h) y un tronco de cono de radio R de base y altura h.
-
Centro de masa de un cono macizo o de un tronco de cono
La posición yc centro de masa de una figura cónica de revolución alrededor del eje Y se calcula mediante la fórmula
Para integrar se ha de relacionar x e y
La integral es inmediata
El denominador es el volumen del tronco de altura h.
Cuando h=H tenemos el centro de masas de un cono macizo de radio R y altura H
El denominador de yc es el volumen del cono πR2H/3
Calculamos la posición del centro de masas de cada unas de las dos porciones de arena: un tronco de cono y de un cono invertido, respecto del origen situado en el vértice común de ambos conos.
-
Cono de altura (H-h) situado en la porción superior del reloj de arena (véase la figura de arriba)
El radio r de la base del cono invertido es
Su volumen es
La posición del centro de masas se encuentra a (H-h)/4 de la base o a y1=3(H-h)/4 del vértice donde está situado el origen.
-
La posición del centro de masas del tronco de cono
La hemos calculado anteriormente. Está a yc de la base del tronco de cono o a –(H-yc) del origen situado en el vértice. Su posición y2=-H+yc es
El volumen del tronco de cono V2 lo hemos calculado ya
-
El centro de masas del conjunto formado por el cono invertido superior y el tronco de cono inferior es
V=V1+V2 es el volumen total, es decir, del cono de radio R y altura H, V=πR2H/3, como puede comprobarse fácilmente.
Velocidad del c.m.
Derivando con respecto del tiempo obtenemos la velocidad del c.m.
El flujo es
Aceleración del c.m.
Derivando respecto del tiempo obtenemos la aceleración del c.m.
La aceleración del c.m. es positiva y tiende a infinito cuando h→H, es decir, cuando se agota la arena de la parte superior.
Calculamos también la aceleración del c.m. mediante la expresión (1) obtenida en el primer apartado
Para un reloj de arena formado por dos conos iguales unidos por sus vértices,
por lo que
La masa total de arena es
La aceleración del c.m. es
Altura de la arena en el recipiente cónico inferior.
El flujo f de arena es constante, al cabo de un cierto tiempo t, la arena llena el volumen V=f·t/ρ de un tronco de cono de altura h. Ya hemos calculado la fórmula del volumen de un tronco de cono.
Conocido el radio de la base R del cono y su altura H, tenemos que resolver una ecuación cúbica, para hallar la altura h del tronco de cono, en el instante t.
Esta ecuación se resuelve por procedimientos numéricos en el programa interactivo
Ejemplo
- Radio de la base del cono, R=0.5 m
- Altura del cono H=0.5 m
- Densidad de la arena ρ=2500 kg/m3
- Flujo de arena f=0.13 kg/s
En un instante dado t la altura h del tronco de cono es de 0.20 m. Calcular el instante t, la posición del c.m. y la diferencia de fuerzas ΔF=Mac que señala la balanza.
-
Instante t
-
Posición del c.m.
-
La fuerza que mide la balanza es
Calculamos el volumen del tronco de cono de altura h=0.2 m
La masa de arena contenida en este volumen es m=ρ·V=2500·0.103=256.6 kg
Como el flujo constante de arena es f=dm/dt=0.13 kg/s,
m=f·t, t=1974 s.
Como vemos el efecto es muy pequeño, y para medirlo experimentalmente (véase el artículo citado en las referencias) es preciso emplear una balanza que mida una masa elevada con una gran precisión.
Actividades
Se introduce
-
El radio R de la base del cono (en cm), en el control titulado Radio cono.
-
El flujo f (en kg/s), en el control titulado Flujo.
-
La altura H del cono se ha fijado en el valor H=0.5 m
-
La densidad de la arena se ha fijado en el valor ρ=2500 kg/m3.
Se pulsa el botón titulado Nuevo
-
Cuando el reloj está parado, su peso es Mg
-
Cuando está en marcha, su peso es algo mayor N
La diferencia es ΔF=N-Mg=Mac
La balanza mide esta diferencia. Al principio cuando el reloj está parado ΔF=0, pero luego, se incrementa hasta que tiende (teóricamente) a infinito cuando deja de fluir la arena procedente del recipiente cónico superior. Por ejemplo, cuando la balanza marca 1.72e-5 N quiere decir, 1.72·10-5 N.
Vemos como el c.m. del sistema, señalado por un punto de color rojo, desciende a medida que cae la arena del recipiente cónico superior hacia el inferior.
Referencias
Shen K. Y., Scott B. The hourglass problem. Am. J. Phys. 53 (8) August 1985, pp. 787-788.

