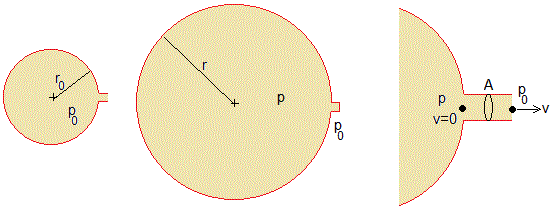
Presión producida por la curvatura de una superficie

Young y Laplace dedujeron de forma independiente en 1805 la fórmula de la diferencia de presión entre el interior y el exterior de una superficie esférica de radio R.

La fórmula de Young-Laplace demuestra que la presión en el interior de de una superficie esférica es siempre mayor que en el exterior, que la diferencia de presión se incrementa cuando disminuye al radio de dicha superficie y que se hace cero cuando la superficie es plana (radio infinito).

Los líquidos tienden a minimizar su superficie. Por esta razón, las gotas tienen forma esférica en ausencia de gravedad. La tensión superficial tiende a reducir el área de la superficie y por tanto, el volumen de la gota. La diferencia de presión tiende a incrementar el volumen de la gota, la condición de equilibrio se alcanza cuando ambas tendencias se compensan.

La ecuación Young-Laplace para una burbuja

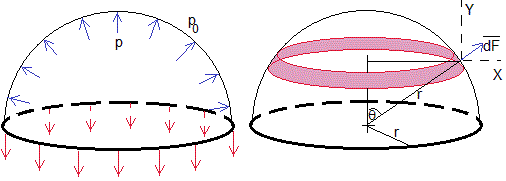
Vamos a mostrar que en el interior de una gota o una burbuja en equilibrio hay una presión superior a la exterior. Este exceso de presión es debido a la curvatura de la superficie límite de separación.

Las fuerzas de presión ejercen una fuerza que es normal a la superficie. Supongamos que la presión en el interior de la burbuja es p y en el exterior es p₀, entonces la fuerza sobre una porción (en color rosa) dA=(2πrsinθ)(r·dθ) de la lámina es dF=(p-p₀)dA, y tiene dirección radial, su componente Y es (p-p₀)dA·cosθ. Las componentes X de las fuerzas se anulan por simetría

$F_{1} = \int_{0}^{π / 2} ((p - p_{0}) 2 π r \sin θ \cdot r d θ) \cos θ = - 2 π (p - p_{0}) r^{2} {\frac{\cos^{2} θ}{2} |}_{0}^{π / 2} = (p - p_{0}) π r^{2}$

Una burbuja está formada por dos láminas superficiales esféricas muy próximas entre sí. Consideremos la mitad de la burbuja y busquemos las fuerzas que mantienen a esa porción en equilibrio.

La fuerza que origina la diferencia de presión es F₁= (p-p₀)·πr²
Fuerza originada por la tensión superficial

La mitad izquierda de la burbuja (no representada) ejerce una fuerza hacia la izquierda igual a dos veces la tensión superficial por el perímetro (flechas rojas en la figura) F₂=2γ·2πr

En el equilibrio F₁=F₂

$p - p_{0} = \frac{4 γ}{r}$

la diferencia de presiones es tanto mayor cuanto menor es el radio r. Esta expresión es un caso particular de la denominada ley de Laplace.

El factor cuatro aparece por que una pompa de jabón tiene dos caras: interior y exterior. En el caso de una gota de agua, solamente hay una cara por lo que la diferencia de presión se reduce a la mitad.

La ecuación de Young-Laplace para una gota

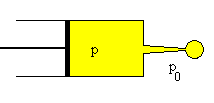
Supongamos una gota que se forma en el extremo de una jeringa al desplazar el émbolo, tal como se indica en la figura.

Sea p₀ la presión exterior. Para formar la gota de radio r es necesario aplicar mediante el émbolo una presión p algo mayor que p₀.

El trabajo realizado por el émbolo sobre el líquido al desplazarse es p·dV. Pero la gota realiza un trabajo p₀·dV sobre su entorno ya que desplaza el aire al incrementar su volumen dV. Ambos volúmenes son iguales debido a que el líquido es incomprensible.

El trabajo total sobre el líquido será dW=(p-p₀)·dV

Este trabajo se emplea en incrementar la superficie de la gota, mientras se mantiene la temperatura y el volumen del líquido constantes. dW=γdA

Igualando ambos trabajos y teniendo en cuenta las fórmulas del área y del volumen de una superficie esférica.

$\begin{array}{l} V = \frac{4}{3} π r^{3} A = 4 π r^{2} \\ d V = 4 π r^{2} \cdot d r d A = 8 π r \cdot d r \\ p - p_{0} = \frac{2 γ}{r} \end{array}$

La ecuación Young-Laplace para la superficie de un líquido

Consideremos un elemento diferencial dS situada en un punto P de una superficie convexa de un fluido, y sea $\hat{n}$ , el vector unitario normal a dicha superficie.

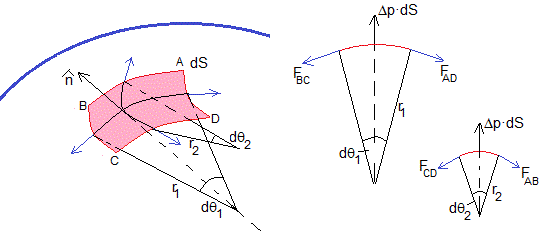
Un plano que contenga la dirección normal define un elemento diferencial de curva con un radio de curvatura r. Al girar el plano que contiene la normal, obtenemos el valor mínimo y máximo del radio de curvatura (a la derecha en la figura). Estos dos planos son perpendiculares. Sea r₂ el mínimo radio de curvatura y r₁ el máximo.

El área del elemento diferencial de superficie dS=(r₁dθ₁)(r₂dθ₂)

La fuerza que genera la diferencia de presión Δp entre el interior y exterior de la superficie tiene la dirección normal, su módulo es, Δp·dS=Δp(r₁dθ₁)(r₂dθ₂)

Las fuerzas que origina la tensión superficial actúan en los bordes del elemento diferencial de superficie, señaladas con cuatro flechas de color azul. Sus módulos son

F_AD=γ|AD|=γ(r₂dθ₂)
F_BC=γ|BC|=γ(r₂dθ₂)
F_AB=γ|AB|=γ(r₁dθ₁)
F_CD=γ|CD|=γ(r₁dθ₁)

La dirección es tangente a la superficie en el borde del elemento diferencial de superficie, tal como se indica en la parte derecha de la figura

Las componentes perpendiculares a la dirección normal de estas fuerzas se cancelan, las componentes a lo largo de la dirección normal se suman.

En el equilibrio, la fuerza generada por la diferencia de presión entre el interior y exterior de la superficie tiene que ser igual a la resultante de las fuerzas debidas a la tensión superficial que actúa en los cuatro lados del elemento diferencial de superficie dS. Teniendo en cuenta que para un ángulo muy pequeño, sinx≈x

$\begin{array}{l} Δ p \cdot d S = F_{A D} \frac{d θ_{1}}{2} + F_{B C} \frac{d θ_{1}}{2} + F_{C D} \frac{d θ_{2}}{2} + F_{A B} \frac{d θ_{2}}{2} \\ Δ p \cdot (r_{2} d θ_{2}) (r_{1} d θ_{1}) = γ (r_{2} d θ_{2}) d θ_{1} + γ (r_{1} d θ_{1}) d θ_{2} \\ Δ p = γ (\frac{1}{r_{1}} + \frac{1}{r_{2}}) \end{array}$

Esta ecuación nos proporciona la diferencia de presión Δp a través de la superficie del líquido en cualquier punto en términos de la tensión superficial y de los dos principales radios de curvatura (máximo y mínimo) en dicho punto. Proporciona el exceso de presión Δp cuando se pasa hacia el lado de la superficie donde se encuentra el centro de curvatura

Radios de curvatura

Una superficie de revolución que se obtiene haciendo girar la función z=f(x) alrededor del eje Z.

Trazamos un plano tangente a la superficie de la gota que pasa por el punto P. La recta perpendicular a dicho plano que pasa por P es la normal.

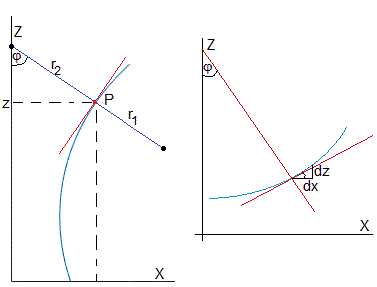
Se obtiene el perfil de la superficie de revolución, cortando por el plano y=0, que viene descrito por la función z=f(x).

El radio de curvatura principal r₁ (una cantidad positiva) se obtiene igual que para cualquier otra función de una variable.

$r_{1} = \frac{{(1 + {(\frac{d z}{d x})}^{2})}^{3 / 2}}{| \frac{d^{2} z}{d x^{2}} |}$

Como se trata de una superficie de revolución, el centro de curvatura está en el eje y el radio de curvatura r₂, es

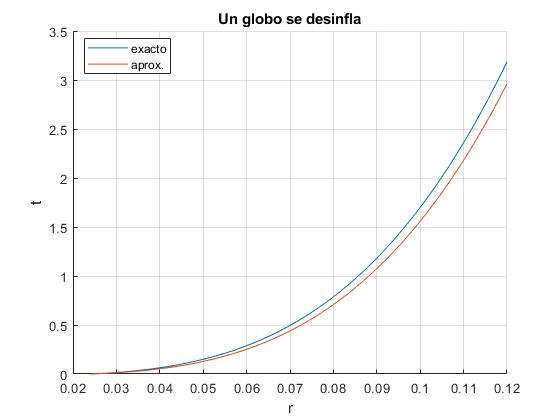
$\begin{array}{l} r_{2} = \frac{x}{\sin φ}, \sin φ = \frac{\tan φ}{\sqrt{1 + \tan^{2} φ}} = \frac{\frac{d z}{d x}}{\sqrt{1 + {(\frac{d z}{d x})}^{2}}} \\ r_{2} = \frac{x \sqrt{1 + {(\frac{d z}{d x})}^{2}}}{| \frac{d z}{d x} |} \end{array}$

Desinflando un globo

En la página titulada Un globo que asciende en la atmósfera estudiamos la relación entre la diferencia presión Δp y el radio r del globo

En esta página, estudiaremos los globos que utilizan los niños en las fiestas y que se inflan soplando aire con sus bocas. Supondremos que la relación entre la diferencia presión Δp y el radio del globo, es similar a la de una pompa de jabón

$p - p_{0} = \frac{2 γ}{r}$

γ es la tensión superficial del material elástico del que está hecho el globo, p es la presión en el interior del globo, poco más grande que la presión atmosférica p₀

Supondremos que el globo sin inflar tiene forma esférica de radio r₀. Vamos a calcular el tiempo que tarda un globo inflado hasta un radio r en desinflarse

Calculamos la masa m de aire que hay dentro de un globo que ha sido inflado hasta el radio r>r₀, aplicando la ecuación de los gases perfectos

$\begin{array}{l} p V = \frac{m}{M} R T \\ m = p V \frac{M}{R T} = (p_{0} + \frac{2 γ}{r}) (\frac{4}{3} π r^{3}) \frac{M}{R T} = \frac{4 π}{3} \frac{p_{0} M}{R T} (r^{3} + \frac{2 γ}{p_{0}} r^{2}) = \frac{4 π}{3} ρ (r^{3} + \frac{2 γ}{p_{0}} r^{2}) \end{array}$

R es la constante de los gases, T es la temperatura y M es la peso molecular

Supondremos que el aire que sale por el orificio del globo de sección A, se comporta como un fluido ideal y por tanto, es aplicable la ecuación de Bernoulli

$p = p_{0} + \frac{1}{2} ρ v^{2}$

La masa de aire que sale por el orificio en la unidad de tiempo es

$\frac{d m}{d t} = - A ρ v = - A ρ \sqrt{\frac{2 (p - p_{0})}{ρ}} = - 2 A \sqrt{\frac{ρ γ}{r}}$

Escribimos la ecuación diferencial en términos de la variable r ya que conocemos la masa de aire m que hay en un globo de radio r

$\begin{array}{l} \frac{4 π}{3} ρ (3 r^{2} + \frac{4 γ}{p_{0}} r) \frac{d r}{d t} = - 2 A \sqrt{\frac{ρ γ}{r}} \\ 2 π (r^{5 / 2} + \frac{4 γ}{3 p_{0}} r^{3 / 2}) d r = - A \sqrt{\frac{γ}{ρ}} d t \end{array}$

Integramos, sabiendo que en el instante t=0, el radio del globo es r y en el instante t el globo se ha desinflado, su radio es r₀

$\begin{array}{l} 2 π \int_{r}^{r_{0}} (r^{5 / 2} + \frac{4 γ}{3 p_{0}} r^{3 / 2}) d r = - A \sqrt{\frac{γ}{ρ}} \int_{0}^{t} d t \\ t = \frac{4 π}{A} \sqrt{\frac{ρ}{γ}} {\frac{1}{7} (r^{7 / 2} - r_{0}^{7 / 2}) + \frac{4 γ}{15 p_{0}} (r^{5 / 2} - r_{0}^{5 / 2})} \end{array}$

Ejemplo

Area del orificio, A=1.79·10^-5 m²
Radio final del globo al desinflarse, r₀=0.024 m
Presión atmosférica, p₀=1.013·10⁵ Pa
Densidad del aire, ρ=1.225 kg/m³
Tensión superficial, γ=500 N/m

Se representa en el eje X, el radio r en m y en el eje Y, el tiempo t en s

Comprobamos que el primer término correspondiente a la potencia 7/2 de r es dominante

A=1.79e-5; %área del orificio
r0=0.024; %radio final del globo
p0=1.013e5; %presión atmosférica
rho=1.225; %densidad del aire
gamma=500; %tensión superficial
hold on
t1=@(r) 4*pi*sqrt(rho/gamma)*((r.^(7/2)-r0^(7/2))/7
+4*gamma*(r.^(5/2)-r0^(5/2))/(15*p0))/A;
fplot(t1,[r0,0.12])

%se suprime el segundo término, potencia 5/2
t2=@(r) 4*pi*sqrt(rho/gamma)*((r.^(7/2)-r0^(7/2))/7)/A;
fplot(t2,[r0,0.12])
hold off
grid on
legend('exacto','aprox.', 'location', 'best')
xlabel('r')
ylabel('t')
title('Un globo se desinfla')

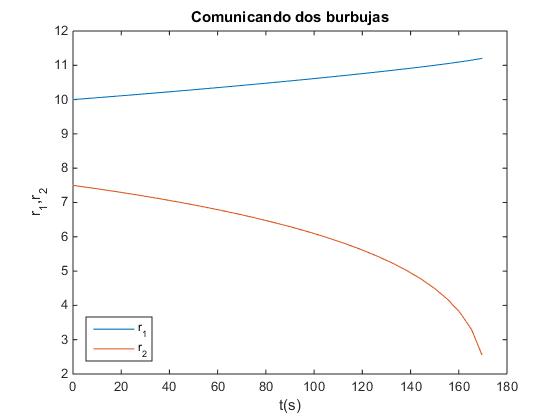
Comunicando dos pompas de jabón

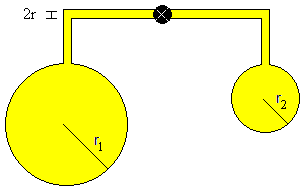
Si ponemos dos pompas de jabón de radios r₁ y r₂ en los extremos de un tubo y abrimos la llave que las comunica veremos que la pompa de jabón de radio menor es "comida" por la pompa de radio mayor.

La diferencia de presión entre el exterior y el interior de una pompa de jabón es muy pequeña comparada con la presión atmosférica. Por tanto, podemos considerar la densidad del aire no cambia (fluido incompresible) cuando pasa de una pompa a la otra.

La diferencia de presión entre las esferas de radio r₁ y de radio r₂ serán

$p_{2} - p_{1} = 4 γ (\frac{1}{r_{2}} - \frac{1}{r_{1}})$

Como consecuencia de la diferencia de presión, el aire circula por el tubo de comunicación con una velocidad dada por el teorema de Bernoulli

$p_{2} - p_{1} = \frac{1}{2} ρ v^{2}$

El volumen de aire que pasa de la segunda esfera a la primera en el tiempo dt es vSdt, siendo S=πR² la sección del tubo que comunica ambas esferas. ρ=1.29 kg/m³ es la densidad del aire

El volumen de la primera esfera aumenta y el de la segunda, disminuye.

$\begin{array}{l} d V_{1} = S v \cdot d t \\ 4 π r_{1}^{2} d r_{1} = S \sqrt{\frac{4 γ (r_{1} - r_{2})}{ρ r_{1} r_{2}}} d t \end{array}$

Hay que resolver la integral por procedimientos numéricos

$\int_{R_{01}}^{R_{1}} \frac{x^{2} d x}{\sqrt{{(V - x^{3})}^{- 1 / 3} - 1 / x}} = \frac{R^{2}}{4} \sqrt{\frac{4 γ}{ρ}} t V = r_{01}^{3} + r_{02}^{3} = r_{1}^{3} + r_{2}^{3}$

Conocido el radio inicial de la esfera izquierda, r₀₁ se calcula el tiempo t cuando dicha esfera alcanza el radio r₀₁≤r₁<V^1/3

La última ecuación, indica que la suma de los volúmenes de las dos esferas es constante. hemos considerado en esta aproximación que el aire es un fluido incomprensible, ya que los cambios de presión que experimenta en el interior de las burbujas son muy pequeños, comparados con la presión atmosférica.

r_01=10; %cm
r_02=7.5; %cm
tension=0.073; %tensión superficial N/m
rCom=0.5; % radio del tubo de comunicación cm
vol=(r_01^3+r_02^3); %volumen total constante
r_1m=vol^(1/3); %máximo valor de r1, r2=0 (desaparece)

cte=rCom^2*sqrt(4*tension/1.29)/4; 
f=@(x) (x.^2)./sqrt((vol-x.^3).^(-1/3)-1./x);
r1=r_01:0.05:r_1m;
t=zeros(0,length(r1));
i=1;
for radio=r1
    t(i)= integral(f,r_01,radio)/(100*cte); %en segundos
    i=i+1;
end
r2= (vol-r1.^3).^(1/3);
plot(t,r1,t,r2)
xlabel('t(s)')
ylabel('r_1,r_2')
legend('r_1','r_2', 'location','southwest')
title('Comunicando dos burbujas')

Nota: La descripción dada en este párrafo, se debe de entender desde el punto de vista cualitativo, explica el fenómeno observado de que dos globos o dos pompas de jabón conectadas por un pequeño tubo de volumen despreciable, la esfera de mayor radio aumenta a costa de la de menor radio, hasta que esta última desaparece. Un análisis termodinámico del problema es demasiado complicado para incluirlo en estas páginas, se puede consultar el artículo de Weinhaus F. citado en las referencias.

Actividades

Se introduce

el radio inicial de cada una de las esferas, en los controles tituladas Radio izquierda y derecha. En la parte izquierda, se representa la esfera de mayor radio.
el valor para la tensión superficial de la pompa de jabón comprendido entre 20·10^-3 y 80·10^-3 N/m, en el control titulado Tensión superficial.
El radio del tubo de comunicación se ha fijado en r=0.5 cm

Se pulsa el botón titulado Nuevo.

Observamos como la burbuja pequeña se hace cada vez más pequeña mientras crece la burbuja grande.

Radio izquierda:
Radio derecha:
Tensión superficial ·10^-3:

Comunicando dos pompas de jabón. Un modelo más elaborado

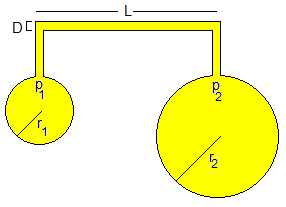
En el instante t=0, los radios de las pompas son R₁ y R₂. Aplicamos la ecuación de los gases ideales

$\begin{array}{l} (p_{0} + \frac{4 γ}{R_{1}}) \frac{4}{3} π R_{1}^{3} = \frac{m_{01}}{M} R T \\ (p_{0} + \frac{4 γ}{R_{2}}) \frac{4}{3} π R_{2}^{3} = \frac{m_{02}}{M} R T \end{array}$

donde m₀₁/M es el número de moles de aire contenido en la pompa izquierda, m₀₂/M es el número de moles contenido en la pompa derecha. T es la temperatura y p₀ es la presión atmosférica.

Se comunican las dos pompas de jabón mediante un tubo de longitud L y diámetro D. En el instante t, los radios de las pompas de jabón son r₁ y r₂

$\begin{array}{l} (p_{0} + \frac{4 γ}{r_{1}}) \frac{4}{3} π r_{1}^{3} = \frac{m_{1}}{M} R T \\ (p_{0} + \frac{4 γ}{r_{2}}) \frac{4}{3} π r_{2}^{3} = \frac{m_{2}}{M} R T \end{array}$

Supondremos que el proceso es isotermo, no cambia la temperatura T. De la conservación de la masa obtenemos

$\begin{array}{l} m_{1} + m_{2} = m_{01} + m_{02} \\ (p_{0} + \frac{4 γ}{r_{1}}) \frac{4}{3} π r_{1}^{3} + (p_{0} + \frac{4 γ}{r_{2}}) \frac{4}{3} π r_{2}^{3} = (p_{0} + \frac{4 γ}{R_{1}}) \frac{4}{3} π R_{1}^{3} + (p_{0} + \frac{4 γ}{R_{2}}) \frac{4}{3} π R_{2}^{3} \end{array}$

Como p₀>>4γ/r, se cumple aproximadamente que

$\begin{array}{l} p_{0} \frac{4}{3} π r_{1}^{3} + p_{0} \frac{4}{3} π r_{2}^{3} \approx p_{0} \frac{4}{3} π R_{1}^{3} + p_{0} \frac{4}{3} π R_{2}^{3} \\ r_{1}^{3} + r_{2}^{3} = R_{1}^{3} + R_{2}^{3} \\ r_{2} = {(R_{1}^{3} + R_{2}^{3} - r_{1}^{3})}^{1 / 3} \end{array}$

Ley de Poiseuille

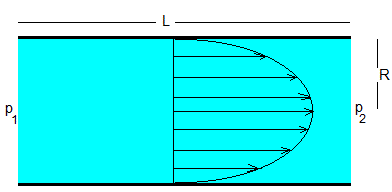
El aire tiene un viscosidad η, fluye por un tubo de longitud L y radio R=D/2 en régimen laminar. Cuando se establece un gradiente de presión es (p₂-p₁)/L, el volumen de fluido en la unidad de tiempo (gasto) es

$G = \frac{π}{8} \frac{p_{1} - p_{2}}{L} \frac{R^{4}}{η}$

Multiplicamos por la densidad del fluido ρ, para obtener la masa de fluido en la unidad de tiempo, cuando se establece un gradiente de presión -dp/dx

$q = \frac{π}{8} (- \frac{d p}{d x}) \frac{R^{4}}{η} ρ$

La ecuación de los gases ideales relaciona la presión y la densidad

$\begin{array}{l} p V = \frac{m}{M} R T \\ p = \frac{ρ}{M} R T \end{array}$

Expresamos el flujo de masa q en función de la presión p

$q = - \frac{π}{8} \frac{R^{4}}{η} \frac{M}{R T} p \frac{d p}{d x}$

Integramos, a la izquierda del tubo la presión es p₁ y a la derecha es p₂

$\begin{array}{l} \int_{p_{1}}^{p_{2}} p \cdot d p = - \frac{8}{π} \frac{η}{R^{4}} \frac{R T}{M} q \int_{0}^{L} d x \\ \frac{1}{2} (p_{2}^{2} - p_{1}^{2}) = - \frac{8}{π} \frac{η}{R^{4}} \frac{R T}{M} q L \\ {(p_{0} + \frac{4 γ}{r_{1}})}^{2} - {(p_{0} + \frac{4 γ}{r_{2}})}^{2} = \frac{16}{π} \frac{η}{R^{4}} \frac{R T}{M} q L \\ 8 γ (\frac{1}{r_{1}} - \frac{1}{r_{2}}) (p_{0} + \frac{2 γ}{r_{1}} + \frac{2 γ}{r_{2}}) = \frac{16}{π} \frac{η}{R^{4}} \frac{R T}{M} q L \\ q = \frac{π R^{4} M γ}{2 η R T L} (\frac{1}{r_{1}} - \frac{1}{r_{2}}) (p_{0} + \frac{2 γ}{r_{1}} + \frac{2 γ}{r_{2}}) \end{array}$

La pompa izquierda disminuye su radio. La masa de aire que contiene disminuye

$\begin{array}{l} d m_{1} = q \cdot d t \\ d m_{1} = \frac{π R^{4} M γ}{2 η R T L} (\frac{1}{r_{1}} - \frac{1}{r_{2}}) (p_{0} + \frac{2 γ}{r_{1}} + \frac{2 γ}{r_{2}}) d t \end{array}$

De la ecuación del gas ideal aplicado a la pompa izquierda

$\begin{array}{l} (p_{0} + \frac{4 γ}{r_{1}}) \frac{4}{3} π r_{1}^{3} = \frac{m_{1}}{M} R T \\ d m_{1} = \frac{M}{R T} {(p_{0} + \frac{4 γ}{r_{1}}) 4 π r_{1}^{2} - \frac{4}{3} π r_{1}^{3} \frac{4 γ}{r_{1}^{2}}} d r_{1} \\ d m_{1} = \frac{M}{R T} \frac{4}{3} π r_{1}^{2} (3 p_{0} + \frac{8 γ}{r_{1}}) d r_{1} \end{array}$

Igualando ambas expresiones obtenemos la ecuación

$\begin{array}{l} \frac{M}{R T} \frac{4}{3} π r_{1}^{2} (3 p_{0} + \frac{8 γ}{r_{1}}) d r_{1} = \frac{π R^{4} M γ}{2 η R T L} (\frac{1}{r_{1}} - \frac{1}{r_{2}}) (p_{0} + \frac{2 γ}{r_{1}} + \frac{2 γ}{r_{2}}) d t \\ \frac{4}{3} r_{1}^{2} (3 p_{0} + \frac{8 γ}{r_{1}}) d r_{1} = \frac{R^{4} γ}{2 η L} (\frac{1}{r_{1}} - \frac{1}{r_{2}}) (p_{0} + \frac{2 γ}{r_{1}} + \frac{2 γ}{r_{2}}) d t \end{array}$

Junto con la ecuación que relaciona r₂ con r₁

$r_{2} = {(R_{1}^{3} + R_{2}^{3} - r_{1}^{3})}^{1 / 3}$

nos permite obtener la variación de r₁ con el tiempo t

Aproximaciones

Dado que la presión atmosférica es muy grande comparada con la presión debido a la curvatura de la pompa

$\begin{array}{l} 3 p_{0} > > \frac{8 γ}{r_{1}}, p_{0} > > \frac{2 γ}{r_{1}} + \frac{2 γ}{r_{2}} \\ 3 p_{0} \frac{4}{3} r_{1}^{2} d r_{1} = \frac{R^{4} γ}{2 η L} (\frac{1}{r_{1}} - \frac{1}{r_{2}}) p_{0} d t \\ \frac{r_{2}}{r_{2} - r_{1}} r_{1}^{3} d r_{1} = \frac{R^{4} γ}{8 η L} d t \\ \int_{R_{1}}^{r_{1}} \frac{r_{1}^{3} {(R_{1}^{3} + R_{2}^{3} - r_{1}^{3})}^{1 / 3}}{{(R_{1}^{3} + R_{2}^{3} - r_{1}^{3})}^{1 / 3} - r_{1}} d r_{1} = \frac{R^{4} γ}{8 η L} t \end{array}$

Ejemplos

Consideramos tres situaciones

Ejemplo 1

Diámetro del tubo, D=3.567 mm
Longitud del tubo, L=0.8415 m
Viscosidad del aire, η=1.8·10^-5 Pa·s
Tensión superficial de la pompa, γ=33.52·10^-3 N/m
Radio inicial de la pompa izquierda, R₁=35 mm
Radio inicial de la pompa derecha, R₂=50 mm

Calculamos los instantes t en los que el diámetro de la pompa izquierda 2r₁ es 32, 30, 28, 25, 20, 15, 10, 3.567 mm

D=3.567e-3; %diámetro tubo
L=0.8415; %longitud tubo
sigma=33.52e-3; %tensión superficial
eta=1.8e-5; %viscosidad
cte=-128*eta*L/(D^4*sigma);

R2=50/2000; %radios iniciales
R1=35/2000;
r1=[32,30,28,25,20,15,10,3.567]/2000; 
t=zeros(1, length(r1));
hold on
for k=1:length(r1)
    f=@(x) x.^3.*(R1^3+R2^3-x.^3).^(1/3)./((R1^3+R2^3-x.^3).^(1/3)-x);
    t(k)=cte*integral(f,R1,r1(k));
    disp([t(k),r1(k)*2000])
    plot([0,t(k)],[35,r1(k)*2000],'ro','markersize',3,'markerfacecolor','r')
end  
hold off
grid on
xlabel('t (s)')
ylabel('d_1 (mm)')
title('Diámetro de la pompa')

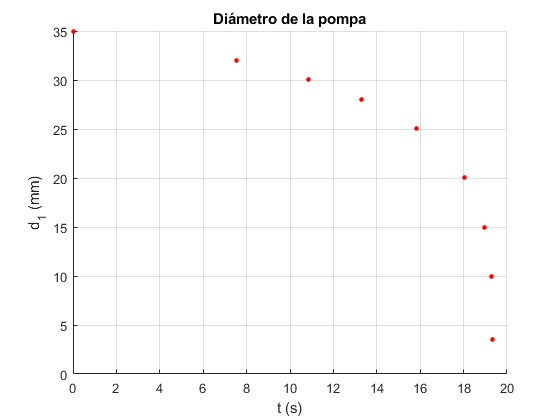
   7.5174    32.0000
   10.8563   30.0000
   13.3078   28.0000
   15.8202   25.0000
   18.0581   20.0000
   18.9674   15.0000
   19.2648   10.0000
   19.3292    3.5670

t (s)	0	7.5174	10.8563	13.3078	15.8202	18.0581	18.9674	19.2648	19.3292
2r₁ (mm)	35	32	30	28	25	20	15	10	3.567

Ejemplo 2

Diámetro del tubo, D=3.567 mm
Longitud del tubo, L=0.8415 m
Viscosidad del aire, η=1.8·10^-5 Pa·s
Tensión superficial de la pompa, γ=33.52·10^-3 N/m
Radio final de la pompa izquierda, r₁=D/2, radio del tubo

Para varios radios iniciales, R₁ y R₂ calculamos el tiempo que tarda la pompa izquierda en alcanzar el radio final D/2, radio del tubo

D=3.567e-3; %diámetro tubo
L=0.8415; %longitud tubo
sigma=33.52e-3; %tensión superficial
eta=1.8e-5; %viscosidad

cte=-128*eta*L/(D^4*sigma);

R1=[25.2,28.2,30.2,33.8,37.8]/2000; 
R2=[47.7,48.5,48.1,47.4,49.5]/2000;
for k=1:length(R1)
    f=@(x) x.^3.*(R1(k)^3+R2(k)^3-x.^3).^(1/3)./((R1(k)^3+R2(k)^3-x.^3).^(1/3)-x);
    t=cte*integral(f,R1(k),D/2);
    disp(t)
end

2R₁ (mm)	25.2	28.2	30.2	33.8	37.8
2R₂ (mm)	47.7	48.5	48.1	47.4	49.5
t (s)	3.9305	6.6644	9.4352	17.2389	29.9443

Ejemplo 3

Diámetro del tubo, D=5.012 mm
Longitud del tubo, L=1.4017 m
Viscosidad del aire, η=1.8·10^-5 Pa·s
Tensión superficial de la pompa, γ=33.52·10^-3 N/m
Radio final de la pompa izquierda, r₁=D/2, radio del tubo

Para varios radios iniciales, R₁ y R₂ calculamos el tiempo que tarda la pompa izquierda en alcanzar el radio final D/2

D=5.012e-3; %diámetro tubo
L=1.4017; %longitud tubo
sigma=33.52e-3; %tensión superficial
eta=1.8e-5; %viscosidad

cte=-128*eta*L/(D^4*sigma);
R1=[30.1,35.2,39.8,43.3,46.5]/2000; 
R2=[61.2,66.7,63.5,64.1,59.8]/2000;
for k=1:length(R1)
    f=@(x) x.^3.*(R1(k)^3+R2(k)^3-x.^3).^(1/3)./((R1(k)^3+R2(k)^3-x.^3).
^(1/3)-x);
    t=cte*integral(f,R1(k),D/2);
    disp(t)
end

2R₁ (mm)	30.1	35.2	39.8	43.3	46.5
2R₂ (mm)	61.2	66.7	63.5	64.1	59.8
t (s)	3.2506	6.3891	12.1404	18.4941	30.2410

Referencias

Pellicer J., García-Morales V., Hernández M. J., On the demostration of Young-Laplace equations in introductory courses. Phys. Educ 35 (2) March 2000, pp. 126-129.

F. Behroozi. The edge profile of liquid spills. Am. J. Phys. 90 (1), January 2022. pp. 10-14

Don S.Lemons, Trevor C. Lipscombe. Of balls, bladders, and balloons: The time required to deflate an elastic sphere. Am. J. Phys. 89 (1), January 2021, pp. 80-83

Weinhaus F., Barker W. On the equilibrium states of interconnected bubbles o balloons. Am. J. Phys. 46 (10) October 1978, pp. 978-982.

WANG Yun-chuang，LI De-yao，AN Yu-kuan，LI Xiang-rain，XING Juan. Study on the dynamic characteristics of the two spherical liquid films communicated by a tubule. College Physics. Volume 23, Issue 5, 20 May 2004