Límites, derivadas.
Límites
Calcular el límite
Límites indeterminados de la forma 0/0 o ∞/∞. Regla de L'Hôpital
Otras formas indeterminadas son 0·∞ y ∞-∞ que se transforman en 0/0 o ∞/∞.
Ejemplos:
>> sym x a; >> y=(x^2+2*x-1)/(x^2+1); >> limit(y,x,1) ans =1 >> limit(sin(a*x)/x,x,0) % alternativamente, limit(sin(a*x)/x) ans =a >> limit((1+a/x)^x,x,inf) %alternativamente, limit((1+a/x)^x,inf) ans =exp(a) >> y=1/(sin(x)^2)-1/x^2; >> limit(y,x,0) ans =1/3 >> y=cos(2*x)^(3/x^2); >> limit(y,x,0) ans =1/exp(6)
La derivada de una función f(x) es el límite
La derivada de y=sin(x) es y'=cos(x)
>> syms x h; >> limit((sin(x+h)-sin(x))/h,h,0) ans =cos(x)
De forma alternativa, podemos calcular las derivadas definiendo la función f(x) como función anónima y aplicando la definición de derivada.
>> syms x h; >> f=@(x) sin(x) >> limit((f(x+h)-f(x))/h,h,0) ans =cos(x)
Definimos la función anónima f(x) con cualquier expresión y podemos calcular su derivada.
Límites por la izquierda y por la derecha
>>syms x; >> limit(x/abs(x),x,0,'left') ans =-1 >> limit(x/abs(x),x,0,'right') ans =1
Derivada de una función
La función
>> syms x; >> y=(sin(x))^2; >> yp=diff(y) yp =2*cos(x)*sin(x) >> ypp=diff(yp) ypp =2*cos(x)^2 - 2*sin(x)^2 >> diff(y,2) ans =2*cos(x)^2 - 2*sin(x)^2
Derivadas parciales (respecto de una variable)
>> syms x y; >> diff(x*sin(x*y),x) ans =sin(x*y) + x*y*cos(x*y) >> diff(x*sin(x*y),y) ans =x^2*cos(x*y)
Comprobar que la función es la solución de la ecuación diferencial que describe las oscilaciones amortiguadas, donde A y b son constantes que se determinan a partir de las condiciones iniciales (posición inicial y velocidad inicial).
>> syms x A b; >> y=A*exp(-2*x)*cos(3*x+b); >> diff(y,2)+4*diff(y)+13*y ans =0
Estudio de una función
Sea la función
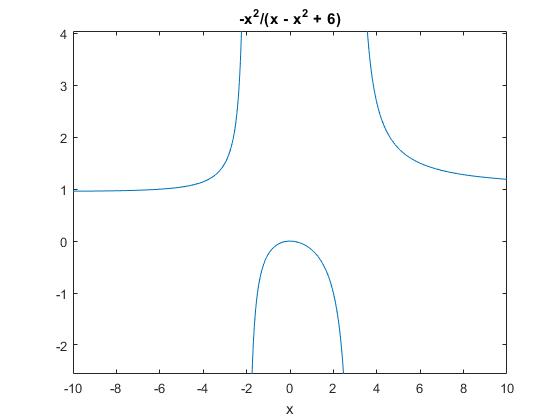
La representamos gráficamente
>> syms x; >> y=x^2/(x^2-x-6); >> ezplot(y,[-10 10])
Puntos de corte con el eje X
Son las raíces de la ecuación
El único punto de corte es (0,0)
>> solve(y) ans = 0 0
Asíntotas
La asíntota horizontal se calcula tomando el límite de f(x) cuando x se aproxima al infinito positivo
>> limit(y,inf) ans =1
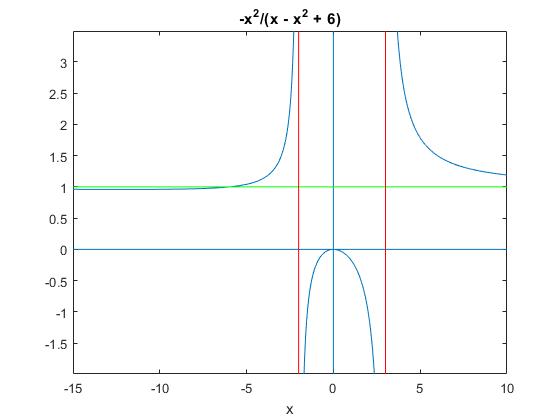
La asíntota horizontal es la recta de ecuación y=1
Las asíntotas verticales se encuentran buscando las raíces del denominador, es decir resolviendo la ecuación x2-x-6=0
>> solve(x^2-x-6) ans = 3 -2
Las asíntotas verticales son las rectas de ecuación x=3, x=-2.
Máximos, mínimos y puntos de inflexión
Los extremos de un función se calculan haciendo la derivada de la función igual a cero.
>> yp=diff(y) yp =- (2*x)/(- x^2 + x + 6) - (x^2*(2*x - 1))/(- x^2 + x + 6)^2 >> solve(yp) ans = 0 -12
Para determinar si es un máximo o un mínimo, calculamos la derivada segunda y determinamos su signo para x=0 y x=-12.
Para determinar los puntos de inflexión igualamos la derivada segunda a cero y obtenemos las raíces
>> ypp=diff(y,2) ypp = - 2/(- x^2 + x + 6) - (2*x^2)/(- x^2 + x + 6)^2 - (2*x^2*(2*x - 1)^2)... /(- x^2 + x + 6)^3 - (4*x*(2*x - 1))/(- x^2 + x + 6)^2 >> simplify(ypp) ans =18/(5*(x - 3)^3) - 8/(5*(x + 2)^3) >> subs(ypp,x,0) ans = -0.3333 >> subs(ypp,x,-12) ans = 5.3333e-004 >> solve(ypp) %puntos de inflexión ans = - 6/7 + (6*6^(1/2)*i)/7 - 6/7 - (6*6^(1/2)*i)/7
- Para x=0, y''<0 hay un máximo
- Para x=-12, y''>0 hay un mínimo
- La curva no tiene puntos de inflexión, la ecuación y''=0, no tiene raíces reales.
Creamos un script para dibujar la función, los ejes y las asóntotas.
syms x; y=x^2/(x^2-x-6); ezplot(y,[-15 10]) asint=limit(y,inf); raices=roots([1,-1,-6]); line([-15 10],[0 0]) %eje horizontal line([0 0],[-5 10]) %eje vertical line([-15 10],[asint asint], 'color','g') %asíntota horizontal line(raices(1)*[1 1],[-5 10],'color','r') %asíntotas verticales line(raices(2)*[1 1],[-5 10],'color','r')
Ejercicio
La ley de distribución de las velocidades moleculares de Maxwell es
La expresión de vmax corresponde a la velocidad de las moléculas para la cual la función presenta un máximo y está directamente relacionada con la temperatura absoluta T.
- Calcular la velocidad vmax de las moléculas para la cual la función presenta un máximo
- Calcular el valor de esta velocidad para las moléculas de oxígeno: m=5.3·10-26 kg, T=300 K, k=1.38·10-23 J/K
- Representar la función f(v) para las moléculas de oxígeno en el intervalo (0, 1500) m/s.
>> syms m v k T pi;
>> y=sqrt((2/pi)*(m/(k*T))^3)*v^2*exp(-m*v^2/(2*k*T));
>> yp=diff(y,v);
>> simplify(yp)
ans =(2^(1/2)*v*(2*T*k - m*v^2)*(m^3/(T^3*k^3))^(1/2))
/(pi^(1/2)*T*k*exp((m*v^2)/(2*T*k)))
>> vp=solve(yp)
vp =
0
(2^(1/2)*(T*k*m)^(1/2))/m
-(2^(1/2)*(T*k*m)^(1/2))/m
>> subs(vp(2),{m,k,T},{5.3e-26,300,1.38e-23})
ans = 395.2549
>> yy=subs(y,{m,k,T},{5.3e-26,300,1.38e-23})
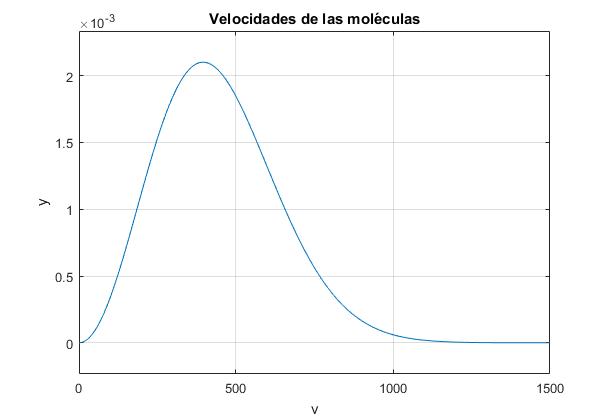
>> ezplot(yy,[0 1500])
>> title('Velocidades de las moléculas')
>> xlabel('v')
>> ylabel ('y')
>> grid on
Función de dos variables
Sea una función f(x,y)
-
Las derivadas parciales respecto de x y de y son
Las derivadas parciales segundas son
Evaluamos el determinante D en los puntos críticos
- Mínimo local, si D>0 y fxx>0,
- Máximo local, si D>0 y fxx<0,
- Puntos de inflexión, si D<0
- Si D=0, indeterminado
Igualándolas a cero, obtenemos un sistema de dos ecuaciones, las raíces (xk,yk) son los puntos críticos
Ejemplo 1
Sea la función f(x,y)=4xy-x4-y4
syms x y;
f=@(x,y) 4*x.*y-x.^4-y.^4;
fx=diff(f,x);
fxx=diff(fx,x);
fy=diff(f,y);
fyy=diff(fy,y);
fxy=diff(fy,x);
eq1=fx==0; %sistema de ecuaciones
eq2=fy==0;
[mx,my]=solve(eq1,eq2);
S=double(mx);
mx=S(imag(S)==0);
S=(double(my));
my=S(imag(S)==0);
de=fxx*fyy-fxy^2;
disp([double(mx),double(my)])
for k=1:length(mx)
disp([subs(de,{x,y},{mx(k),my(k)}), subs(fxx,{x,y},{mx(k),my(k)})])
end
[X,Y]=meshgrid(-2:0.1:2);
z=f(X,Y);
hold on
surf(X,Y,z)
for k=1:length(mx) %puntos críticos
plot3(mx(k),my(k),f(mx(k),my(k)),'ro','markersize',4,'markerfacecolor','r')
end
hold off
grid on
zlim([-5,2])
hold off
grid on
xlabel('x')
ylabel('y')
zlabel('z')
view(60,40)
Los puntos críticos se muestran sobre la superficie en color rojo
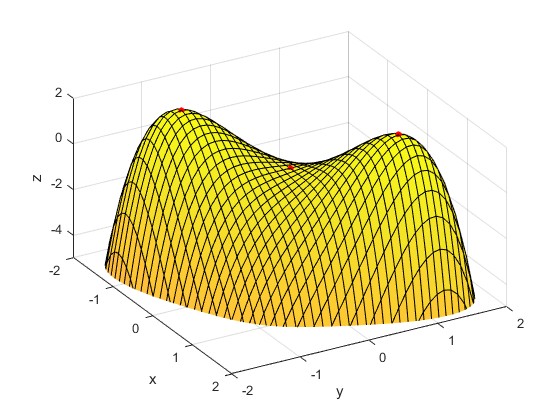
0 0
-1 -1
1 1
[-16, 0]
[128, -12]
[128, -12]
El origen (0, 0) es un punto de inflexión. El determinante es D=-16<0
Los puntos (1, 1) y (-1, -1) son máximos, el determinante D=128>0 y fxx=-12<0
Ejemplo 2
Sea la función f(x,y)=x2+y2+3x+4y
syms x y;
f=@(x,y) x.^2+y.^2+3*x+4*y;
fx=diff(f,x);
fxx=diff(fx,x);
fy=diff(f,y);
fyy=diff(fy,y);
fxy=diff(fy,x);
eq1=fx==0; %sistema de ecuaciones
eq2=fy==0;
[mx,my]=solve(eq1,eq2,[x,y]);
S=double(mx);
mx=S(imag(S)==0);
S=(double(my));
my=S(imag(S)==0);
de=fxx*fyy-fxy^2;
disp([double(mx),double(my)])
for k=1:length(mx) %puntos críticos
disp([subs(de,{x,y},{mx(k),my(k)}), subs(fxx,{x,y},{mx(k),my(k)})])
end
[X,Y]=meshgrid(-3:0.1:0);
z=f(X,Y);
hold on
surf(X,Y,z)
for k=1:length(mx)
plot3(mx(k),my(k),f(mx(k),my(k)),'ro','markersize',4,'markerfacecolor','r')
end
hold off
grid on
xlabel('x')
ylabel('y')
zlabel('z')
view(60,45)
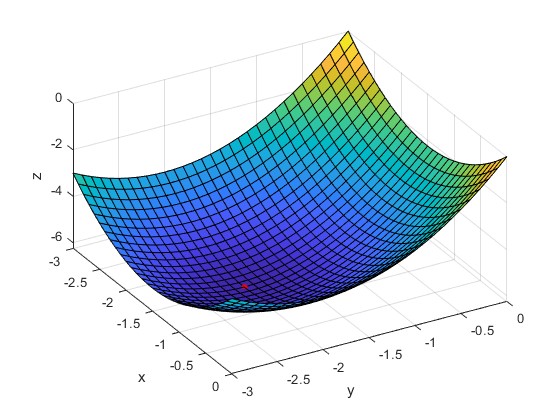
-1.5000 -2.0000 [4, 2]
El punto (-1.5, -2.0) es un mínimo. El determinante es D=4>0 y y fxx=2>0
Ejemplo 3
Sea la función f(x,y)=x2-y2-3x+5y+3
syms x y;
f=@(x,y) x.^2-y.^2-3*x+5*y+3;
fx=diff(f,x);
fxx=diff(fx,x);
fy=diff(f,y);
fyy=diff(fy,y);
fxy=diff(fy,x);
eq1=fx==0; %sistema de ecuaciones
eq2=fy==0;
[mx,my]=solve(eq1,eq2,[x,y]);
S=double(mx);
mx=S(imag(S)==0);
S=(double(my));
my=S(imag(S)==0);
de=fxx*fyy-fxy^2;
disp([double(mx),double(my)])
for k=1:length(mx)
disp([subs(de,{x,y},{mx(k),my(k)}), subs(fxx,{x,y},{mx(k),my(k)})])
end
[X,Y]=meshgrid(0:0.1:5);
z=f(X,Y);
hold on
surf(X,Y,z)
for k=1:length(mx) %puntos críticos
plot3(mx(k),my(k),f(mx(k),my(k)),'ro','markersize',4,'markerfacecolor','r')
end
hold off
grid on
xlabel('x')
ylabel('y')
zlabel('z')
view(60,45)
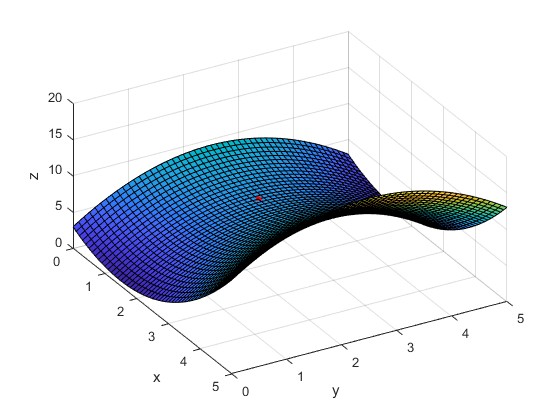
1.5000 2.5000 [-4, 2]
El punto (1.5, 2.5) es un punto de inflexión. El determinante es D=-4<0
Ejemplos en el curso de Física
Límites: limit
Movimiento de dos cuerpos bajo la fuerza de atracción mutua
El oscilador forzado. El estado transitorio y su evolución hacia el estado estacionario
Respuesta de un oscilador a una fuerza impulsiva (I)
Derivadas: diff
Errores en las medidas indirectas
El oscilador forzado. El estado estacionario
Representación gráfica: ezplot
Movimiento sobre la cúpula semiesférica con rozamiento
Movimiento de dos cuerpos bajo la fuerza de atracción mutua
El oscilador forzado. El estado transitorio y su evolución hacia el estado estacionario
Respuesta de un oscilador a una fuerza impulsiva (II)
Modos normales de vibración. Oscilaciones de tres partículas unidas por muelles elásticos
Oscilaciones forzadas en un sistema formado por partículas unidas por muelles. Fuerza periódica
Oscilaciones forzadas en un sistema formado por partículas unidas por muelles. Fuerza no periódica
Se calienta un líquido periódicamente
Las leyes del enfriamiento y calentamiento
Descenso de un paracaidista. Fuerza de rozamiento proporcional al cuadrado de la velocidad
Un globo que asciende en la atmósfera
Referencias
M. Y. Tufail, S. Gul, S. A. A. Hashmi. Interactive MATLAB GUI for exploring extreme values in bivariate functions. Revista Mexicana de Física E 23 010212 1–6. January–June 2026