Ecuaciones diferenciales de primer orden

Variables separadas

${\displaystyle \begin{array}{l}\frac{dx}{dt}=f(t)·g(x)\\ {\displaystyle \int \frac{dx}{g(x)}}={\displaystyle \int f(t)dt}\\ G(x)=F(t)+c\end{array}}$

Carga de un condensador a través de una resistencia

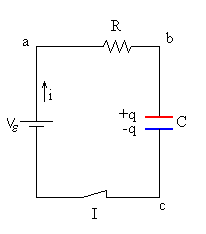
Considérese el circuito en serie de la figura. Inicialmente el condensador está descargado. Si se cierra el interruptor I la carga empieza a fluir produciendo corriente en el circuito, el condensador se empieza a cargar. Una vez que el condensador adquiere la carga máxima, la corriente cesa en el circuito.

En el circuito de la figura tendremos que la suma V_ab+V_bc+V_ca=0

La ecuación del circuito es

${\displaystyle iR+\frac{q}{C}-V_{\epsilon }=0}$

Teniendo en cuenta que la intensidad se define como la carga que atraviesa la sección del circuito en la unidad de tiempo, i=dq/dt, tendremos la siguiente ecuación para integrar

${\displaystyle \begin{array}{l}R\frac{dq}{dt}=V_{\epsilon }-\frac{q}{C}\\ {\displaystyle \underset{0}{\overset{q}{\int }}\frac{dq}{C{V}_{\epsilon }-q}}=\frac{1}{RC}{\displaystyle \underset{0}{\overset{t}{\int }}dt}q=C{V}_{\epsilon }\left(1-\exp \left(\frac{-t}{RC}\right)\right)\end{array}}$

Derivando con respecto al tiempo, obtenemos la intensidad en función del tiempo

${\displaystyle i=\frac{dq}{dt}=\frac{V_{\epsilon }}{R}\exp \left(\frac{-t}{RC}\right)}$

>> syms R C V;
>> q=dsolve('R*Dq=V-q/C','q(0)=0')
q =C*V - (C*V)/exp(t/(C*R))
>> i=diff(q)
i =V/(R*exp(t/(C*R)))

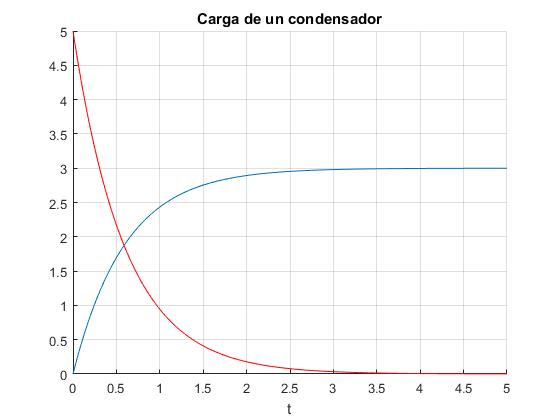
Damos valores a R=2, C=0.3, V=10 y representamos la carga q del condensador y la intensidad i de la corriente en función del tiempo en la misma ventana gráfica

>> qq=subs(q,{R,C,V},{2,0.3,10})
qq =3 - 3/exp((5*t)/3)
>> ii=subs(i,{R,C,V},{2,0.3,10})
ii =5/exp((5*t)/3)
 
>> hold on
>> ezplot(qq,[0,5])
>> h=ezplot(ii,[0,5]);
>> set(h,'color','r')
>> grid on
>> hold off
>> ylim([0,5])
>> title('Carga de un condensador')

Ecuaciones diferenciales lineales de primer orden

${\displaystyle \frac{dx}{dt}+P(t)x=Q(t)}$

La solución de la ecuación diferencial homogénea con Q(t)=0, es

${\displaystyle \begin{array}{l}\frac{dx}{x}=-P(t)dt\\ \ln (x)=-{\displaystyle \int P(t)dt}\\ x(t)=C(t)\exp \left(-{\displaystyle \int P(t)dt}\right)\end{array}}$

Se introduce esta solución en la ecuación diferencial no homogénea

${\displaystyle \begin{array}{l}\frac{dx}{dt}+P(t)x=Q(t)\\ \frac{dC(t)}{dt}\exp \left(-{\displaystyle \int P(t)dt}\right)-P(t)\exp \left(-{\displaystyle \int P(t)dt}\right)C(t)+P(t)C(t)\exp \left(-{\displaystyle \int P(t)dt}\right)=Q(t)\\ \frac{dC(t)}{dt}=Q(t)\exp \left({\displaystyle \int P(t)dt}\right)\\ C(t)={\displaystyle \int Q(t)\exp \left({\displaystyle \int P(t)dt}\right)·dt}+c\end{array}}$

La solución completa es

${\displaystyle x(t)=\exp \left(-{\displaystyle \int P(t)dt}\right)\left\{c+{\displaystyle \int Q(t)\exp \left({\displaystyle \int P(t)dt}\right)dt}\right\}}$

donde la constante c se determina a partir de las condiciones iniciales

Ejemplo. Sea la ecuación diferencial

${\displaystyle \frac{dx}{dt}-\tan t·x=\cos t,\{\begin{array}{l}P(t)=-\tan t\\ Q(t)=\cos t\end{array}}$

Calculamos las integrales

${\displaystyle \begin{array}{l}{\displaystyle \int P(t)dt}=-{\displaystyle \int \tan t·dt}=-{\displaystyle \int \frac{\sin t}{\cos t}·dt}=\ln (\cos t)\\ {\displaystyle \int Q(t)\exp \left({\displaystyle \int P(t)dt}\right)dt}={\displaystyle \int \cos t·\cos t·dt=\frac{1}{2}{\displaystyle \int \left(1+\cos (2t)\right)dt=\frac{t}{2}+\frac{\sin (2t)}{4}}}\end{array}}$

El resultado es

${\displaystyle x(t)=\frac{1}{\cos t}\left\{c+\frac{t}{2}+\frac{\sin (2t)}{4}\right\}=\frac{c}{\cos t}+\frac{t}{2\cos t}+\frac{1}{2}\sin t}$

>> x=dsolve('Dx-tan(t)*x=cos(t)')
x =(t/2 + sin(2*t)/4)/cos(t) + C2/cos(t)

Ecuación de Bernoulli

${\displaystyle \frac{dx}{dt}+P(t)x=Q(t)x^{m}m\ne \mathrm{0,}m\ne 1}$

Se reduce a una lineal haciendo la sustitución x=u·v

${\displaystyle \begin{array}{l}\frac{dx}{dt}-\frac{4}{t}x=t\sqrt{x}\\ x=u·v\\ u\frac{dv}{dt}+\frac{du}{dt}v-\frac{4}{t}u·v=t\sqrt{u·v}\\ \left(\frac{du}{dt}-\frac{4}{t}u\right)·v+u\frac{dv}{dt}=t\sqrt{u·v}\{\begin{array}{l}\frac{du}{dt}-\frac{4}{t}u=0u=t^4\\ u\frac{dv}{dt}=t\sqrt{u·v}\end{array}\\ t^4\frac{dv}{dt}=t\sqrt{t^4·v}v={\left(\frac{1}{2}\ln \left|t\right|+C\right)}^2\\ x=u·v=t^4{\left(\frac{1}{2}\ln \left|t\right|+C\right)}^2\end{array}}$

>> x=dsolve('Dx-4*x/t=t*sqrt(x)')
x =                       0
 (t^4*(C3 + log(t))^2)/4

Ecuaciones diferenciales exactas

Sea la ecuación diferencial

${\displaystyle \begin{array}{l}\begin{array}{l}\left(3t^2+6t{x}^2\right)dt+\left(6t^{2}x+4x^3\right)dx=0\\ P(t,x)dt+Q(t,x)dx=0\end{array}\hfill \\ Q(t,x)\frac{dx}{dt}=-P(t,x)\hfill \end{array}}$

Si se cumple que

${\displaystyle \frac{\partial P}{\partial x}=\frac{\partial Q}{\partial t}}$

La ecuación diferencial se puede escribir de la forma .

${\displaystyle \begin{array}{l}dU(t,x)=P(t,x)dt+Q(t,x)dx=0\\ P(t,x)=\frac{\partial U}{\partial t}Q(t,x)=\frac{\partial U}{\partial x}\end{array}}$

Integramos

${\displaystyle \begin{array}{l}U={\displaystyle \int P(t,x)dt}+\phi (x)\\ U={\displaystyle \int (3t^2+6t{x}^2)dt}+\phi (x)=t^3+3t^2{x}^2+\phi (x)\\ Q(t,x)=\frac{\partial U}{\partial x}\\ 6t^{2}x+4x^3=6t^{2}x+\frac{d\phi }{dx}\\ \frac{d\phi }{dx}=4x^3\phi (x)=x^4+C\\ U=t^3+3t^2{x}^2+\phi (x)=t^3+3t^2{x}^2+x^4=C\end{array}}$

MATLAB no sabe calcular la solución de esta ecuación diferencial mediante dsolve para este caso,

>> syms t x;
>> P=3*t^2+6*t*x^2;
>> Q=6*t^2*x+4*x^3;
>> diff(P,x)
ans =12*t*x
>> diff(Q,t)
ans =12*t*x
>> x=dsolve('Dx+(3*t^2+6*t*x^2)/(6*t^2*x+4*x^3)=0') 
x =    ((9*t^4 - 4*t^3 + C7)^(1/2)/2 - (3*t^2)/2)^(1/2)
....

Para obtener la solución vamos a reproducir el procedimiento empleado para obtener la solución analítica.

>> syms x t;
>> P=3*t^2+6*t*x^2;
>> Q=6*t^2*x+4*x^3;
>> diff(P,x)
ans =12*t*x
>> diff(Q,t)
ans =12*t*x %diferencial exacta
>> u1=int(P,t) %integra P respecto de t
u1 =t^2*(3*x^2 + t)
>> du2=Q-diff(u1,x)
du2 =4*x^3
>> u2=int(du2,x) %integra respecto de x
u2 =x^4
>> u=u1+u2 
u =t^2*(3*x^2 + t) + x^4

Factor integrante

Si la diferencial no es exacta es posible encontrar un factor integrante μ, tal que

${\displaystyle \frac{\partial }{\partial x}\left(\mu P\right)=\frac{\partial }{\partial t}\left(\mu Q\right)}$

Este factor integrante se puede calcular fácilmente en dos casos:

${\displaystyle \begin{array}{l}\frac{1}{Q}\left(\frac{\partial P}{\partial x}-\frac{\partial Q}{\partial t}\right)=f(t),\mu =\exp \left({\displaystyle \int f(t)dt}\right)\hfill \\ \frac{1}{P}\left(\frac{\partial Q}{\partial t}-\frac{\partial P}{\partial x}\right)=g(x),\mu =\exp \left({\displaystyle \int g(x)dx}\right)\hfill \end{array}}$

La ecuación diferencial se puede escribir de la forma

${\displaystyle \begin{array}{l}dU(t,x)=\mu P(t,x)dt+\mu Q(t,x)dx=0\\ \mu P(t,x)=\frac{\partial U}{\partial t}\mu Q(t,x)=\frac{\partial U}{\partial x}\end{array}}$

• Ejemplo 1

Sea la ecuación diferencial

${\displaystyle \begin{array}{l}P(t,x)dt+Q(t,x)dx=0\\ \left(2tx+t^{2}x+\frac{x^3}{3}\right)dt+(t^2+x^2)dx=0\end{array}}$

Calculamos el factor integrante μ de la primera forma

${\displaystyle \frac{1}{Q}\left(\frac{\partial P}{\partial x}-\frac{\partial Q}{\partial t}\right)=\frac{1}{t^2+x^2}\left(2t+t^2+x^2-2t\right)=1\text{,}\mu =e^t}$

Obtenemos la solución de la ecuación diferencial

${\displaystyle \begin{array}{l}U={\displaystyle \int \mu P(t,x)dt}+\phi (x)\\ U={\displaystyle \int e^t\left(2tx+t^{2}x+\frac{x^3}{3}\right)dt}+\phi (x)=\\ =x{t}^2{e}^t+\frac{x^3}{3}{e}^t+\phi (x)\\ \mu Q(t,x)=\frac{\partial U}{\partial x}\\ e^t\left(x^2+t^2\right)=t^2{e}^t+x^2{e}^t+\frac{d\phi }{dx}\\ \frac{d\phi }{dx}=0\phi (x)=C\\ U=x{t}^2{e}^t+\frac{x^3}{3}{e}^t+C=e^{t}x\left(t^2+\frac{x^2}{3}\right)=C\end{array}}$

>> clear
>> syms x t c;
>> P=2*t*x+x*t^2+x^3/3;
>> Q=t^2+x^2;
>> diff(P,x)
ans =t^2 + 2*t + x^2
>> diff(Q,t)
ans =2*t %no es diferencial exacta
>> dmu=(diff(P,x)-diff(Q,t))/P
dmu =(t^2 + x^2)/(t^2*x + 2*t*x + x^3/3)
>> dmu=(diff(P,x)-diff(Q,t))/Q
dmu =1
>> mu=exp(t); %factor integrante
>> u1=int(P*mu,t)
u1 =(x*exp(t)*(3*t^2 + x^2))/3
>> du2=mu*Q-diff(u1,x)
du2 =exp(t)*(t^2 + x^2) - (2*x^2*exp(t))/3 - (exp(t)*(3*t^2 + x^2))/3
>> simplify(du2)
ans =0
>> u=u1+c
u =(x*exp(t)*(3*t^2 + x^2))/3+c

• Ejemplo 2

${\displaystyle \left(xt\right)dt+\left(t^2-1-\alpha +x\right)dx=0}$

Comprobamos que no es diferencial exacta

${\displaystyle \begin{array}{l}\frac{\partial P}{\partial x}=\frac{\partial Q}{\partial t}\\ t\ne 2t\end{array}}$

Buscamos un factor integrante μ de la segunda forma

${\displaystyle \begin{array}{l}\frac{1}{P}\left(\frac{\partial Q}{\partial t}-\frac{\partial P}{\partial x}\right)=g(x),\mu =\exp \left({\displaystyle \int g(x)dx}\right)\\ \frac{1}{xt}\left(2t-2\right)=\frac{1}{x},\mu =\exp \left({\displaystyle \int \frac{1}{x}dx}\right)=\exp \left(\ln x\right)=x\end{array}}$

Comprobamos que es diferencial exacta

${\displaystyle \begin{array}{l}\frac{\partial \left(\mu P\right)}{\partial x}=\frac{\partial \left(\mu Q\right)}{\partial t}\\ \frac{\partial \left(x^{2}t\right)}{\partial x}=\frac{\partial \left(x\left(t^2-1-\alpha +x\right)\right)}{\partial t}\\ 2xt=2xt\end{array}}$

Obtenemos la solución de la ecuación diferencial

${\displaystyle \begin{array}{l}U={\displaystyle \int \mu P(t,x)dt+\phi (x)=}{\displaystyle \int x·xt·dt+\phi (x)=}{x}^2\frac{t^2}{2}+\phi (x)\\ \mu Q(t,x)=\frac{\partial U}{\partial x}\\ x\left(t^2-1-\alpha +x\right)=x{t}^2+\frac{\partial \phi }{\partial x}\\ \frac{\partial \phi }{\partial x}=x^2-\left(1+\alpha \right)x\\ \phi (x)={\displaystyle \int \left(x^2-\left(1+\alpha \right)x\right)dx}=\frac{x^3}{3}-\frac{1+\alpha }{2}{x}^2+C\\ U(x,t)=x^2\frac{t^2}{2}+\frac{x^3}{3}-\frac{1+\alpha }{2}{x}^2=C\end{array}}$

Ecuación diferencial lineal homogénea de coeficientes constantes

${\displaystyle \begin{array}{l}{a}_1\frac{d^{n}x}{d{t}^n}+a_2\frac{d^{n-1}x}{d{t}^{n-1}}+\mathrm{...}{a}_n\frac{dx}{dt}+a_{n+1}x=0\\ x=C\exp (s·t)\\ a_1{s}^n+a_2{s}^{n-1}+\mathrm{...}+a_{n}s+a_{n+1}=0\end{array}}$

Raíces reales
Si las raíces s₁,s₂,...s_n de la ecuación característica son distintas, la solución de la ecuación diferencial es

${\displaystyle x=C_1\exp (s_1·t)+C_2\exp (s_2·t)+\mathrm{...}{C}_n\exp (s_n·t)}$

Si las raíces se repiten, por ejemplo la raíz s₁ se repite m veces, s₁=s₂=...s_m

${\displaystyle x=\left(C_1+C_{2}t+\mathrm{...}+C_m{t}^{m-1}\right)\exp (s_1·t)+C_{m+1}\exp (s_{m+1}·t)+\mathrm{...}{C}_n\exp (s_n·t)}$

Raíces complejas

Si las raíces de la ecuación característica son complejas, estas aparecen por pares, s₁=a+bi y s₂=a-bi que son conjugadas.

${\displaystyle \begin{array}{l}{C}_1\exp (at+bi·t)+C_2\exp (at-bi·t)=\\ \exp (at)\left(C_1·\exp (bi·t)+C_2·\exp (-bi·t)\right)=\\ \exp (at)\left((C_1+C_2)\cos (bt)+i(C_1-C_2)\sin (bt)\right)=\\ \exp (at)\left(B_1\cos (bt)+B_2\sin (bt)\right)=A\exp (at)\sin (bt+\phi )\end{array}}$

La más importante de las ecuaciones diferenciales lineales homogéneas es la de segundo orden con coeficientes constantes p y q.

${\displaystyle \frac{d^{2}x}{d{t}^2}+p\frac{dx}{dt}+qx=0}$

La ecuación característica es s²+ps+q=0. La solución general se escribe en una de las tres formas siguientes:

${\displaystyle \begin{array}{l}x=C_1\exp (s_{1}t)+C_2\exp (s_{2}t)\text{raíces reales distintas}\\ x=(C_1+C_2·t)\exp (s_{1}t)\text{raíces reales iguales}\\ x=\exp (at)\left(C_1\cos (bt)+C_2\sin (bt)\right)\text{raíces complejas}\end{array}}$

Ecuación diferencial no homogénea

${\displaystyle a_1\frac{d^{n}x}{d{t}^n}+a_2\frac{d^{n-1}x}{d{t}^{n-1}}+\mathrm{...}{a}_n\frac{dx}{dt}+a_{n+1}x=f(t)}$

La solución se compone de la suma de dos términos: la correspondiente a la ecuación homogénea y de una solución particular.

Coeficientes indeterminados

1. Ecuación diferencial homogénea con condiciones iniciales dadas.

${\displaystyle \begin{array}{l}\frac{d^{2}x}{d{t}^2}+\frac{dx}{dt}-6t=0\\ t=0\{\begin{array}{l}t=3\\ \frac{dx}{dt}=-1\end{array}\end{array}}$

La ecuación característica es s²+2s-6=0, cuyas raíces son s=-3 y s=2;

${\displaystyle \begin{array}{l}x=C_1{e}^{-3t}+C_2{e}^{2t}\\ t=0\{\begin{array}{l}3=C_1+C_2\\ -1=-3C_1+2C_2\end{array}\\ x=\frac{7}{5}{e}^{-3t}+\frac{8}{5}{e}^{2t}\end{array}}$

>> x=dsolve('D2x+Dx-6*x=0','x(0)=3','Dx(0)=-1')
x =(8*exp(2*t))/5 + 7/(5*exp(3*t))

2. Ecuación diferencial no homogénea

${\displaystyle \begin{array}{l}\frac{d^{2}x}{d{t}^2}+4\frac{dx}{dt}+3x=3e^{-2t}\\ t=0\{\begin{array}{l}x=1\\ \frac{dx}{dt}=-1\end{array}\end{array}}$

La solución de esta ecuación diferencial se compone de la suma de dos términos, la homogénea y la particular
La ecuación característica es s²+4s+3=0, cuyas raíces son s=-1 y s=-3; La solución de la ecuación diferencial homogénea es:

${\displaystyle x=C_1{e}^{-t}+C_2{e}^{-3t}}$

La solución particular es x₁=Aexp(-2t) que sustituimos en la ecuación diferencial para determinar el valor de A

${\displaystyle \begin{array}{l}4A{e}^{-2t}+4·(-2)A{e}^{-2t}+3A{e}^{-2t}=3e^{-2t}\\ A=-3\end{array}}$

La solución completa es

${\displaystyle x=C_1{e}^{-t}+C_2{e}^{-3t}-3e^{-2t}}$

Determinamos las constantes C₁ y C₂ a partir de las condiciones iniciales

${\displaystyle \begin{array}{l}x=C_1{e}^{-t}+C_2{e}^{-3t}-3e^{-2t}\\ t=0\{\begin{array}{l}1=C_1+C_2-3\\ -1=-C_1-3C_2+6\end{array}\\ x=\frac{5}{2}{e}^{-t}+\frac{3}{2}{e}^{-3t}-3e^{-2t}\end{array}}$

>> x=dsolve('D2x+4*Dx+3*x=3*exp(-2*t)','x(0)=1','Dx(0)=-1')
x =5/(2*exp(t)) - 3/exp(2*t) + 3/(2*exp(3*t))

3. Ecuación diferencial no homogénea, cambia la solución particular

${\displaystyle \begin{array}{l}\frac{d^{2}x}{d{t}^2}+4\frac{dx}{dt}+3x=-2e^{-t}\\ t=0\{\begin{array}{l}t=1\\ \frac{dt}{dt}=-1\end{array}\end{array}}$

La ecuación característica es s²+4s+3=0, cuyas raíces son s=-1 y s=-3; La solución de la ecuación diferencial homogénea es:

${\displaystyle x=C_1{e}^{-t}+C_2{e}^{-3t}}$

La solución particular es x₁=A·t·exp(-t) que sustituimos en la ecuación diferencial para determinar el valor de A

${\displaystyle \begin{array}{l}-2A{e}^{-t}+At{e}^{-t}+4·\left(A{e}^{-t}-At{e}^{-t}\right)+3At{e}^{-t}=-2e^{-t}\\ A=-1\end{array}}$

La solución completa es

${\displaystyle x=C_1{e}^{-t}+C_2{e}^{-3t}-t{e}^{-t}}$

Determinamos las constantes C₁ y C₂ a partir de las condiciones iniciales

${\displaystyle \begin{array}{l}x=C_1{e}^{-t}+C_2{e}^{-3t}-t{e}^{-t}\\ t=0\{\begin{array}{l}1=C_1+C_2\\ -1=-C_1-3C_2-1\end{array}\\ x=\frac{3}{2}{e}^{-t}-\frac{1}{2}{e}^{-3t}-t{e}^{-t}\end{array}}$

>> x=dsolve('D2x+4*Dx+3*x=-2*exp(-t)','x(0)=1','Dx(0)=-1')
x =3/(2*exp(t)) - 1/(2*exp(3*t)) - t/exp(t)

4. Otros ejemplos

${\displaystyle 2\frac{d^{2}x}{d{t}^2}-\frac{dx}{dt}-x=4t{e}^{2t}}$

La ecuación característica es 2s²-s-1=0, cuyas raíces son s=1 y s=-1/2

La solución particular es de la forma x₁=(At+B)exp(2t). Calculamos los coeficientes A y B en la ecuación diferencial

${\displaystyle \begin{array}{l}2e^{2t}\left(4A+4B+4At\right)-e^{2t}\left(A+2B+2At\right)-e^{2t}\left(B+At\right)=4t{e}^{2t}\\ A=\frac{4}{5}B=-\frac{28}{25}\end{array}}$

La solución general de la ecuación diferencial es

${\displaystyle x=C_1{e}^t+C_2{e}^{-t/2}+e^{2t}\left(\frac{4}{5}t-\frac{28}{25}\right)}$

>> x=dsolve('2*D2x-Dx-x=4*t*exp(2*t)')
x =(4*exp(2*t)*(t - 1))/3 + C11*exp(t) + C12/exp(t/2) - 
(8*exp((5*t)/2)*(5*t - 2))/(75*exp(t/2))
>> simplify(x)
ans =(4*t*exp(2*t))/5 - (28*exp(2*t))/25 + C11*exp(t) + C12/exp(t/2)

${\displaystyle \frac{d^{2}x}{d{t}^2}-2\frac{dx}{dt}+x=t·e^t}$

La ecuación característica es s²-2s+1=0, cuyas raíces son iguales s=1. La solución de la ecuación diferencial homogénea es

${\displaystyle x=C_1{e}^t+C_2{e}^{-t/2}}$

La solución particular es de la forma x₁=(At+B)·t²·exp(t). Calculamos los coeficientes A y B en la ecuación diferencial, dando A=1/6 y B=0.

La solución general de la ecuación diferencial es

${\displaystyle x=\left(C_1+C_{2}t\right)e^t+\frac{1}{6}{t}^3{e}^t}$

>> x=dsolve('D2x-2*Dx+x=t*exp(t)')
x =(t^3*exp(t))/6 + C14*exp(t) + C15*t*exp(t)

${\displaystyle \frac{d^{2}x}{d{t}^2}+t=t\sin (t)}$

La ecuación característica es s²+1=0, cuyas raíces son complejas conjugadas s₁=i, s₂=-i. La solución de la ecuación diferencial homogénea es

${\displaystyle x=C_1\cos (t)+C_2\sin (t)}$

La solución particular es de la forma x₁=t·((At+B)·cos(t)+(Ct+D)·sin(t)).Calculamos los coeficientes A, B, C y D en la ecuación diferencial, dando A=-1/4, B=0, C=0, D=1/4.

La solución general de la ecuación diferencial es

${\displaystyle x=C_1\cos (t)+C_2\sin (t)-\frac{t^2}{4}\cos (t)+\frac{t}{4}\sin (t)}$

>> x=dsolve('D2x+x=t*sin(t)')
x =sin(t)*(sin(2*t)/8 - (t*cos(2*t))/4) + cos(t)*(cos(2*t)/8 + 
(t*sin(2*t))/4 - t^2/4 - 1/8) + C17*cos(t) + C18*sin(t) 
>> simplify(x)
ans =C17*cos(t) - (t^2*cos(t))/4 + C18*sin(t) + (t*sin(t))/4

Referencias

Barenkov, Demidovich, Efimenko..., Problemas y ejercicios de Análisis Matemático. Paraninfo (1975)