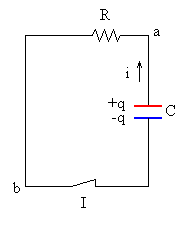
Consideremos ahora el circuito que consta de un condensador, inicialmente cargado con carga Q y una resistencia R y se cierra el interruptor I.

La ecuación del circuito será la siguiente.

V_ab+V_ba=0

• Como la corriente va de a hacia b, el potencial de a es más alto que el potencial de b. Por la ley de Ohm V_ab=iR.
• En el condensador la placa positiva a tiene más potencial que la negativa b, de modo que V_ba=-q/C.

La ecuación del circuito es

${\displaystyle iR-\frac{q}{C}=0}$

Como la carga disminuye con el tiempo i=-dq/dt. La ecuación a integrar es

${\displaystyle \begin{array}{l}-R\frac{dq}{dt}=\frac{q}{C}\\ {\displaystyle \underset{Q}{\overset{q}{\int }}\frac{dq}{q}}=-\frac{1}{RC}{\displaystyle \underset{0}{\overset{t}{\int }}dt}q=Q\exp \left(\frac{-t}{RC}\right)\end{array}}$

La carga del condensador disminuye exponencialmente con el tiempo. Derivando con respecto del tiempo, obtenemos la intensidad, en el sentido indicado en la figura.

${\displaystyle i=-\frac{dq}{dt}=\frac{Q}{RC}\exp \left(\frac{-t}{RC}\right)}$

que disminuye exponencialmente con el tiempo.

Balance energético

• La energía inicial del condensador es

${\displaystyle E_0=\frac{1}{2}\frac{Q^2}{C}}$

• La energía disipada en la resistencia hasta el instante t es

${\displaystyle E_R={\displaystyle \underset{0}{\overset{t}{\int }}{i}^{2}R·dt}=\frac{Q^2}{2C}\left(1-\exp \left(\frac{-2t}{RC}\right)\right)}$

• La energía almacenada en el condensador en forma de campo eléctrico en el instante t es

${\displaystyle E_c=\frac{1}{2}\frac{q^2}{C}=\frac{Q^2}{2C}\exp \left(\frac{-2t}{RC}\right)}$

Comprobamos que E_c=E₀-E_R. La energía en el condensador se disipa en la resistencia. Cuando se completa el proceso de descarga t→∞, toda la energía almacenada en el condensador se ha disipado en la resistencia

Ejemplo:

Sea un condensador de capacidad C=1.5 μF en serie con una resistencia de R=58 kΩ cargado inicialmente con Q=45 μC. Empecemos a contar el tiempo cuando se cierra el interruptor. En el instante t=60 ms

• La carga del condensador es

${\displaystyle q=45·{10}^{-6}\exp \left(\frac{-60·{10}^{-3}}{58000·1.5·{10}^{-6}}\right)=22.6·{10}^{-6}\text{C}}$

• La intensidad es

${\displaystyle i=\frac{{4510}^{-6}}{58000·1.5·{10}^{-6}}\exp \left(\frac{-60·{10}^{-3}}{58000·1.5·{10}^{-6}}\right)=2.60·{10}^{-4}\text{A}}$

• La energía almacenada inicialmente en el condensador es

${\displaystyle E_0=\frac{1}{2}\frac{{(45·{10}^{-6})}^2}{1.5·{10}^{-6}}=6.75·{10}^{-4}\text{J}}$

• La energía disipada en la resistencia es

${\displaystyle E_R=\frac{{(45·{10}^{-6})}^2}{2·1.5·{10}^{-6}}\left(1-\exp \left(\frac{-2·60·{10}^{-3}}{58000·1.5·{10}^{-6}}\right)\right)=5.05·{10}^{-4}\text{J}}$

• La energía acumulada en el condensador es

${\displaystyle E_C=\frac{1}{2}\frac{{(22.6·{10}^{-6})}^2}{1.5·{10}^{-6}}=1.70·{10}^{-4}\text{J}}$

Actividades

Se introduce

• La capacidad C del condensador, en el control titulado Condensador
• La resistencia R, en el control titulado Resistencia
• La carga inicial Q del condensador se ha fijado en el programa

Se pulsa el botón titulado Nuevo

Se observa la descarga del condensador, su color pasa gradualmente de rojo (carga positiva) y azul (carga negativa) a blanco (descargado). A la derecha, se traza la gráfica de la carga q y de la intensidad i en función del tiempo.

Elegir dos valores de la resistencia R₁ y R₂ y dos valores de la capacidad C₁ y C₂ de modo que R₁·C₁=R₂·C₂. Observar como decrece la carga y la intensidad.

Práctica de laboratorio

En el laboratorio utilizamos el circuito mostrado en la fotografía, que consta de una batería, una pila estándar de 1.5 V, una resistencia de 15000 Ω y un condensador de 1000 μF. Seleccionamos carga (Charge) esperamos un tiempo hasta que se carga el condensador. Seleccionamos descarga (Discharge) y medimos la diferencia de potencial entre los extremos del condensador V_bc con un sensor Voltage/Current de PASCO. El programa CAPSTONE recoge los datos, realiza la representación gráfica y el ajuste de dichos datos seleccionado en el menú Exponencial natural.

${\displaystyle V_{bc}=\frac{q}{C}=V_0\exp \left(-\frac{t}{RC}\right)}$

Donde V₀=Q/C es la diferencia de potencial inicial entre los extremos del condensador y Q es la carga inicial del condensador, en el instante t=0

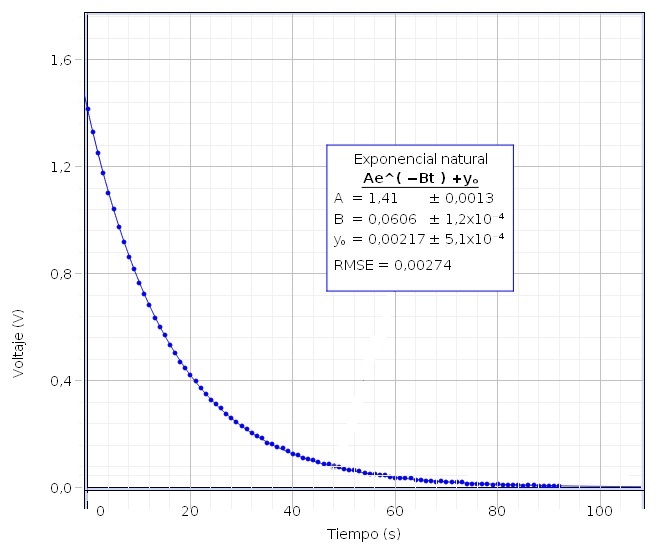
El parámetro B=0.0606, es igual a 1/RC donde R=15000 Ω, por lo que la capacidad del condensador es C=1.1·10^-3 F=1100 μF que es aproximadamente igual a la que hemos obtenido durante el proceso de carga.

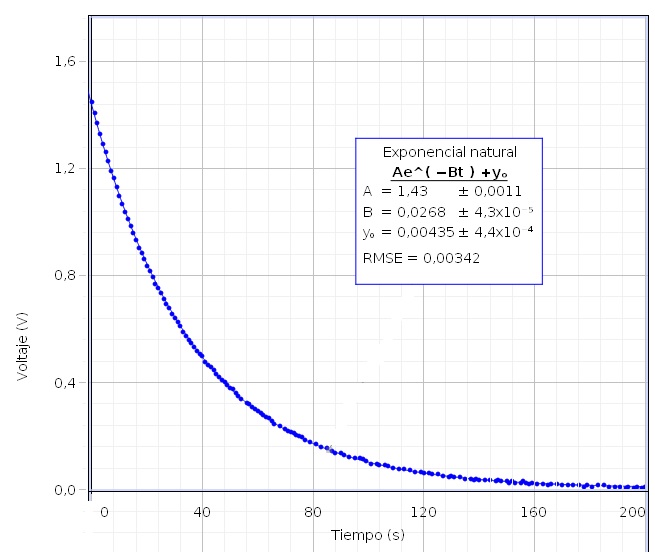
El parámetro B=0.0268, es igual a 1/RC donde R=15000 Ω, por lo que la capacidad del condensador es C=2488 μF que es aproximadamente igual a la que hemos obtenido durante el proceso de carga.

Ajuste de datos con MATLAB

Vamos a utilizar MATLAB para realizar un ajuste lineal de los datos experimentales (t,x) guardados en un fichero de texto generado por DataStudio

Para realizar el ajuste lineal tomamos logaritmos

${\displaystyle \ln V_{bc}=\ln V_0-\frac{t}{RC}}$

Obtenemos la ecuación de una recta cuya pendiente es -1/RC y cuya ordenada en el origen es lnV₀

En primer lugar, preparamos los datos: Con el Bloc de Notas de Windows o similar, eliminamos la cabecera (dos líneas). Seleccionamos en el menú Edición/Reemplazar y sustituímos la coma (que separa la parte entera de los decimales) por un punto. Guardamos el fichero rc_2.txt, que se puede descargar en este enlace y lo colocamos en una carpeta accesible a MATLAB.

Elaboramos un script que realice las siguientes tareas:

1. Importar las dos columnas de datos con el comando load
2. Extraer la primera columna de los datos de tiempo y guardarla en el vector t
3. Extraer la segunda columna que corresponde a los datos de las diferencia de potencial V_bc y guardar su logaritmo log(V_bc) en el vector x.
4. Representar los datos experiementales
5. En el menú seleccionamos Tools/Basic Fitting, aparece un cuadro de diálogo donde marcamos la casilla linear en Plot fits. A continuación, pulsamos la flecha hacia la derecha --> para mostrar los coeficientes p1 y p2 del polinomio (recta) y=p1*x+p2 de ajuste.

load rc_2.txt
t=rc_2(:,1);
x=log(rc_2(:,2));
hold on
%representa los datos experimentales
plot(t,x,'o','markersize',2,'markerfacecolor','b')
title('Descarga de un condensador')
xlabel('tiempo (s)')
ylabel('Voltaje (V)')
grid on

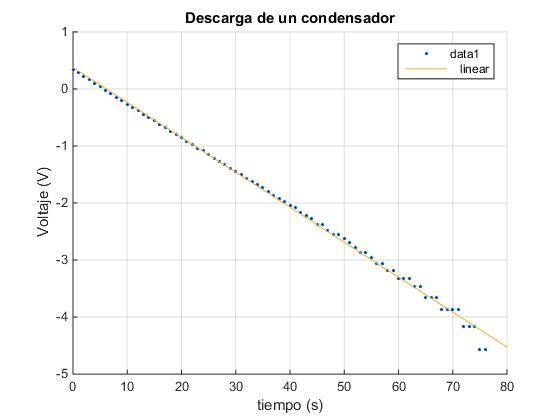
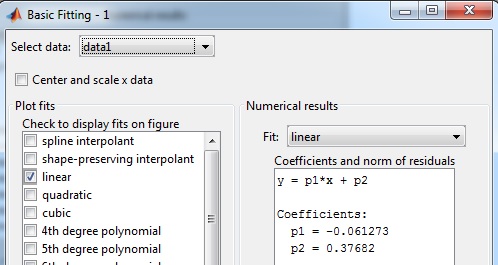
La diferencia de potencial V₀ inicial entre los extremos del condensador vale exp(0.37682)=1.46 V y el cociente 1/RC=0.061273. Si la resistencia del circuito R=15000 Ω, la capacidad del condensador vale C=1088 μF