Movimiento de una porción rectilínea de corriente en un campo no homogéneo
Por una porción de corriente AB de longitud L y masa m circula una corriente de intensidad i, puede deslizar sin rozamiento por el plano horizontal XY debido a las fuerzas que ejerce un campo magnético no homogéneo producido por una corriente rectilínea indefinida i0 situada en el eje Y.
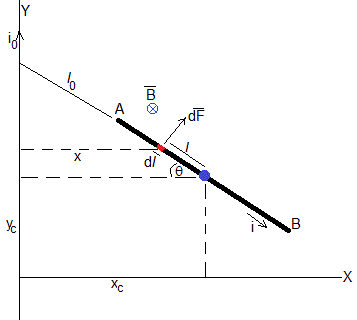
En un instante t la posición del centro de la varilla es (xc, yc) y forma un ángulo θ con el eje X. Se tomarán positivos los ángulos en el sentido de las agujas del reloj
Aplicando la ley de Ampère, calculamos el campo producido por la corriente rectilínea indefinida en la posición (x, y) del elemento de corriente de longitud dl (en color rojo)
cuyo dirección es perpendicular al plano XY y de sentido (hacia dentro) indicado en la figura (regla de la mano derecha).
La fuerza sobre el elemento de longitud dl es
La dirección es perpendicular a la porción de corriente, el sentido indicado en la figura
Traslación del c. m.
Las componentes Fx y Fy de dicha fuerza son
Las ecuaciones del movimiento de traslación del c. m. son
Rotación alrededor de un eje perpendicular que pasa por el c. m.
Calculamos el momento de las fuerzas que se ejercen sobre la varilla respecto del centro de masas (punto de color azul)
Se compone de dos dos momentos en sentidos contrarios: el que ejercen las fuerzas sobre la porción a la izquierda del c. m. y el que ejercen las fuerzas sobre la porción de corriente situada a la derecha del c. m.
Sabiendo que el momento de inercia de una varilla de masa m y longitud L alrededor de un eje perpendicular a la varilla que pasa por su c. m. es . La ecuación de la diámica de rotación es
Solución numérica
Resolvemos el sistema de tres ecuaciones diferenciales
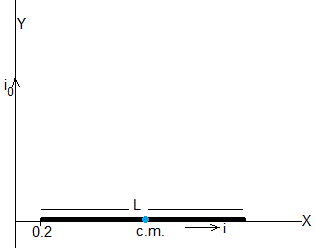
Con las siguientes condiciones iniciales:
Establecemos los valores de las variables:
- Intensidad de la corriente rectilínea indefinida, i0=10 0000 A
- Intensidad de la porción de corriente rectilínea, i= 1 A
- Longitud de la porción de corriente rectilínea, L= 1 m
- Masa de la porción de corriente rectilínea, m=0.1 kg
Representamos la trayectoria del centro de masas
Representamos el ángulo girado θ alrededor del eje perpendicular que pasa por el c. m. en función del tiempo t
Representamos las componentes de la velocidad de traslación del centro de masas vx, vy y la velocidad angular de rotación ω=dθ/dt alrededor del eje perpendicular que pasa por el c. m. en función del tiempo t
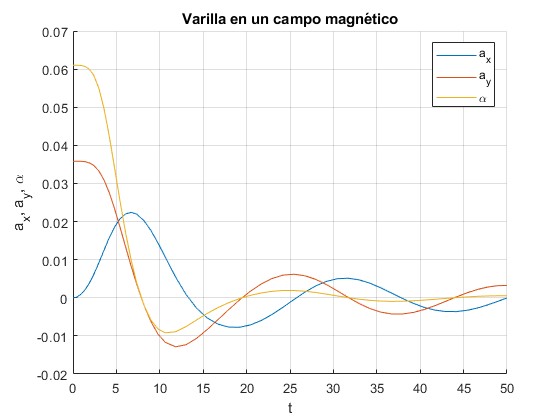
Representamos las componentes de la aceleración del centro de masas dvx/dt, dvy/dt y la aceleración angular de rotación α=dω/dt alrededor del eje perpendicular que pasa por el c. m. en función del tiempo t
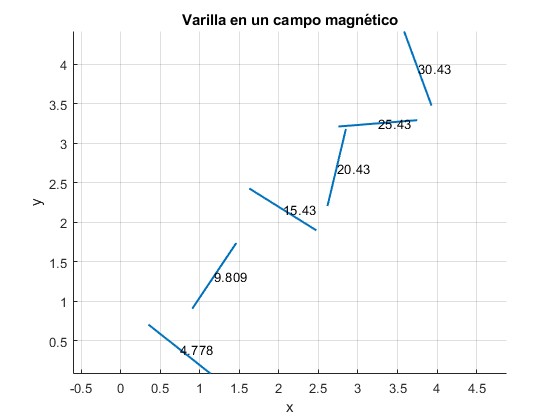
Representamos la posición de la varilla en varios instantes
i0=10000;
i=1;
m=0.1;
L=1;
kx_y=2*1e-7*i*i0/m;
k_m=kx_y*12/L^2;
%x(1)=x, x(2)=dx/dt, x(3)=y, x(4)=dy/dt, x(5)=th, x(6)=dth/dt
fg=@(t,x)[x(2);kx_y*tan(x(5))*log((2*x(1)+L*cos(x(5)))/(2*x(1)-L*cos(x(5))));
x(4); kx_y*log((2*x(1)+L*cos(x(5)))/(2*x(1)-L*cos(x(5)))); x(6);
k_m*(-L+x(1)*log((2*x(1)+L*cos(x(5)))/(2*x(1)-L*cos(x(5))))
/cos(x(5)))/cos(x(5))];
[t,x]=ode45(fg,[0,50],[0.2+L/2, 0,0,0,0,0]);
plot(x(:,1),x(:,3))
grid on
xlabel('x')
ylabel('y');
title('Varilla en un campo magnético')
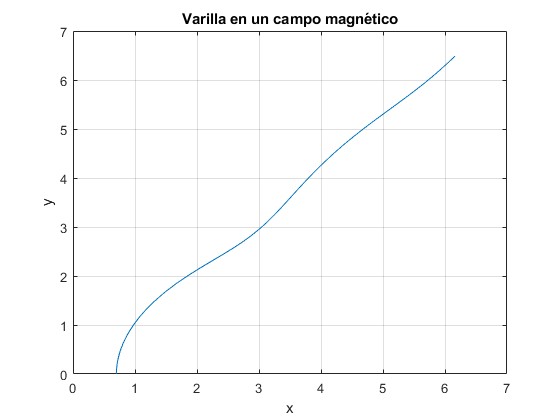
Cambiamos la línea de código

i0=10000;
i=1;
m=0.1;
L=1;
kx_y=2*1e-7*i*i0/m;
k_m=kx_y*12/L^2;
%x(1)=x, x(2)=dx/dt, x(3)=y, x(4)=dy/dt, x(5)=th, x(6)=dth/dt
fg=@(t,x)[x(2);kx_y*tan(x(5))*log((2*x(1)+L*cos(x(5)))/(2*x(1)-L*cos(x(5))));
x(4); kx_y*log((2*x(1)+L*cos(x(5)))/(2*x(1)-L*cos(x(5)))); x(6);
k_m*(-L+x(1)*log((2*x(1)+L*cos(x(5)))/(2*x(1)-L*cos(x(5))))/
cos(x(5)))/cos(x(5))];
[t,x]=ode45(fg,[0,50],[0.2+L/2, 0,0,0,0,0]);
hold on
plot(t,x(:,2))
plot(t,x(:,4))
plot(t,x(:,6))
hold off
grid on
xlabel('t')
legend('v_x', 'v_y', '\omega','location','best')
ylabel('v_x, v_y, \omega');
title('Varilla en un campo magnético')

i0=10000;
i=1;
m=0.1;
L=1;
kx_y=2*1e-7*i*i0/m;
k_m=kx_y*12/L^2;
%x(1)=x, x(2)=dx/dt, x(3)=y, x(4)=dy/dt, x(5)=th, x(6)=dth/dt
fg=@(t,x)[x(2);kx_y*tan(x(5))*log((2*x(1)+L*cos(x(5)))/(2*x(1)-L*cos(x(5))));
x(4); kx_y*log((2*x(1)+L*cos(x(5)))/(2*x(1)-L*cos(x(5)))); x(6);
k_m*(-L+x(1)*log((2*x(1)+L*cos(x(5)))/(2*x(1)-L*cos(x(5))))/
cos(x(5)))/cos(x(5))];
[t,x]=ode45(fg,[0,50],[0.2+L/2, 0,0,0,0,0]);
hold on
a_x=kx_y*tan(x(:,5)).*log((2*x(:,1)+L*cos(x(:,5)))./
(2*x(:,1)-L*cos(x(:,5))));
a_y=kx_y*log((2*x(:,1)+L*cos(x(:,5)))./(2*x(:,1)-L*cos(x(:,5))));
alpha=k_m*(-L+x(:,1).*log((2*x(:,1)+L*cos(x(:,5)))./
(2*x(:,1)-L*cos(x(:,5))))./cos(x(:,5)))./cos(x(:,5));
plot(t,a_x)
plot(t,a_y)
plot(t,alpha)
hold off
grid on
xlabel('t')
legend('a_x', 'a_y', '\alpha','location','best')
ylabel('a_x, a_y, \alpha');
title('Varilla en un campo magnético'
i0=10000;
i=1;
m=0.1;
L=1;
kx_y=2*1e-7*i*i0/m;
k_m=kx_y*12/L^2;
%x(1)=x, x(2)=dx/dt, x(3)=y, x(4)=dy/dt, x(5)=th, x(6)=dth/dt
fg=@(t,x)[x(2);kx_y*tan(x(5))*log((2*x(1)+L*cos(x(5)))/(2*x(1)-L*cos(x(5))));
x(4); kx_y*log((2*x(1)+L*cos(x(5)))/(2*x(1)-L*cos(x(5)))); x(6);
k_m*(-L+x(1)*log((2*x(1)+L*cos(x(5)))/(2*x(1)-L*cos(x(5))))/
cos(x(5)))/cos(x(5))];
[t,x]=ode45(fg,[0,50],[0.2+L/2, 0,0,0,0,0]);
for k=5:5:30
m=find(round(t)==k);
i=m(1);
x1=x(i,1)-L*cos(x(i,5))/2;
x2=x(i,1)+L*cos(x(i,5))/2;
y1=x(i,3)+L*sin(x(i,5))/2;
y2=x(i,3)-L*sin(x(i,5))/2;
line([x1,x2],[y1,y2],'lineWidth',1.5)
text(x(i,1), x(i,3), num2str(t(i),4))
end
axis equal
grid on
xlabel('x')
ylabel('y');
title('Varilla en un campo magnético')
Animación
Para crear la animación se resuelve el sistema de tres ecuaciones diferenciales por el procedimiento de Runge-Kutta
Referencias
Lu Haig-peng. The motion of a finite-length straight conductor in a non-uniform magnetic field. College Physics. 11 November 2025, Volume 44, Issue 9

