Momentos de inercia
Momento de inercia de una distribución de masas puntuales
Tenemos que calcular la cantidad
donde xi es la distancia de la partícula de masa mi al eje de rotación.
Una varilla delgada de 1 m de longitud tiene una masa despreciable. Se colocan 5 masas de 1 kg cada una, situadas a 0.0, 0.25, 0.50, 0.75, y 1.0 m de uno de los extremos. Calcular el momento de inercia del sistema respecto de un eje perpendicular a la varilla que pasa a través de
- Un extremo
- De la segunda masa
- Del centro de masa
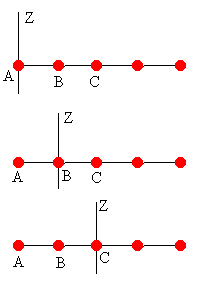
El momento de inercia respecto a un eje perpendicular a la varilla y que pasa por la primera partícula es
El momento de inercia respecto a un eje perpendicular a la varilla y que pasa por la segunda partícula es
El momento de inercia respecto a un eje perpendicular a la varilla y que pasa por la tercera partícula (centro de masas) es
IA=1·02+1·0.252+1·0.52+1·0.752+1·12=1.875 kgm2
IB=1·0.252+1·02+1·0.252+1·0.52+1·0.752=0.9375 kgm2
IC=1·0.52+1·0.252+1·02+1·0.252+1·0.52=0.625 kgm2
El teorema de Steiner nos facilta el cálculo de los momentos de inercia. Conocido IC calculamos IA e IB, sabiendo las distancias entre los ejes paralelos AC=0.5 m y BC=0.25 m.
La fórmula que tenemos que aplicar es
I=IC+Md2
- IC es el momento de inercia del sistema respecto de un eje que pasa por el centro de masa
- I es el momento de inercia respecto de un eje paralelo al anterior
- M es la masa total del sistema
- d es la distancia entre los dos ejes paralelos.
IA=IC+5·0.52=0.625+1.25=1.875 kgm2.
IB=IC+5·0.252=0.625+0.3125=0.9375 kgm2.
Momento de inercia mínimo
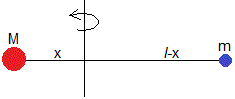
Sean dos masas puntuales M y m unidas por una varilla rígida de longitud l y de masa despreciable. El eje de rotación es perpendicular a la varilla y dista x de la masa puntual M. El momento de inercia es
Representamos I/Ml2 en función de x/l, para m/M=0.5, 1 y 2
hold on
for r=[0.5,1,2] %cociente, m/M
f=@(x) x.^2+r*(1-x).^2;
fplot(f,[0,1])
x_m=r/(1+r); %mínimo, en el centro de masas
line([x_m,x_m],[0,f(x_m)],'lineStyle','--')
end
hold off
grid on
xlabel('x/l')
ylabel('I/Ml^2')
title('Momento de inercia')
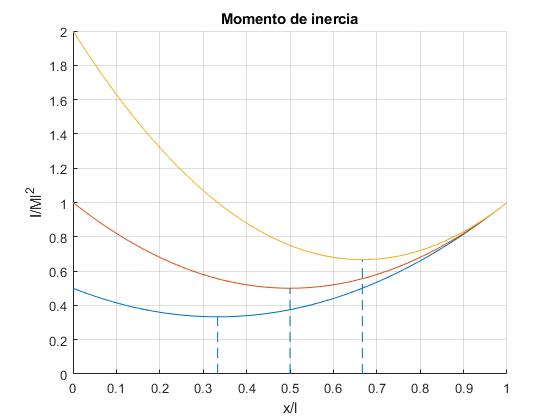
En la representación gráfica del momento de inercia I en función de x vemos, que pasa por un mínimo
que es la posición del centro de masas, señalada en la figura mediante una línea a trazos.
Por ejemplo, para r=0.5, xm/l=1/3=0.33
Momento de inercia de una distribución continua de masa
Pasamos de una distribución de masas puntuales a una distribución continua de masa. La fórmula que tenemos que aplicar es
dm es un elemento de masa situado a una distancia x del eje de rotación
Resolveremos varios ejemplos divididos en dos categorías
-
Cálculo directo mediante la fórmula del momento de inercia
-
Indirectamente, partiendo del momento de inercia de un cuerpo conocido
Momento de inercia de una varilla
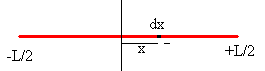
Vamos a calcular el momento de inercia de una varilla de masa M y longitud L respecto de un eje perpendicular a la varilla que pasa por el centro de masas.
La masa dm del elemento de longitud de la varilla comprendido entre x y x+dx es
El momento de inercia de la varilla es
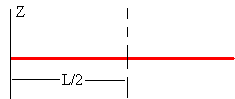
Aplicando el teorema de Steiner, calculamos el momento de inercia de la varilla respecto de un eje perpendicular a la misma que pasa por uno de sus extremos.
Momento de inercia de un disco
Calculamos el momento de inercia de un disco de masa M y radio R respecto de un eje perpendicular al plano del disco y que pasa por su centro.
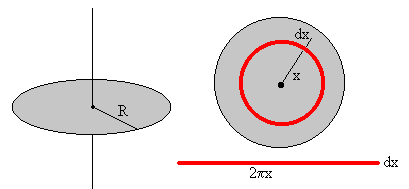
Tomamos un elemento diferencial de masa que dista x del eje de rotación. El elemento es un anillo de radio x y de anchura dx. Si recortamos el anillo y lo extendemos, se convierte en un rectángulo de longitud 2πx y anchura dx, cuya masa es
El momento de inercia del disco es
Momento de inercia de un cono
Sea un cono de masa m, altura h y radio de la base R.
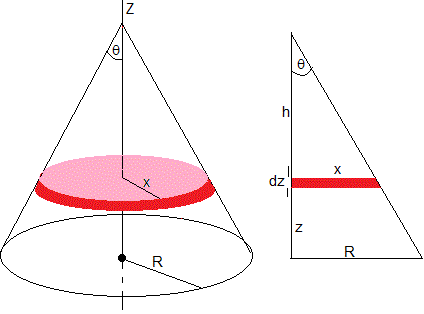
Calculamos el volumen del cono, dividiéndolo en discos radio x y espesor dz, tal como se muestra en la figura. El volumen de cada disco es πx2dz
Relacionamos las variables x y z, figura de la derecha
El volumen de un cono de altura h y radio de la base R es
Sabiendo que la masa dm de cada uno de los discos es
El momento de inercia del cono respecto del eje Z, es la suma de los momentos de inercia de los discos respecto al mismo eje
Utilizando la relación entre las variables x y z
Momento de inercia de un cilindro
Calculamos el momento de inercia de un cilindro de masa M, radio R y longitud L respecto de su eje.
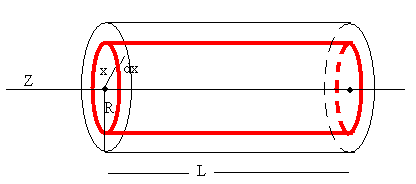
Tomamos un elemento diferencial de masa que dista x del eje de rotación. El elemento es una capa cilíndrica cuyo radio interior es x, exterior x+dx, y de longitud L, tal como se muestra en la figura. La masa dm que contiene esta capa es
El momento de inercia del cilindro es
La misma fórmula que un disco de masa M y radio R
Momento de inercia de un anillo
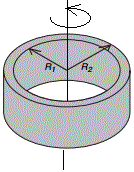
Deducimos la fómula del momento de inercia de una anillo cilíndico de masa M, de radio interior R1 y radio exterior R2
Si la masa M está contenida en el volumen de un anillo de altura h, es
La masa m1 contenida en un cilindro macizo de radio R1 es
La masa m2 contenida en un cilindro macizo de radio R2 es
El momento de inercia del anillo, respecto de su eje de simetría es la diferencia de los momentos de inercia de dos cilindros macizos de radios R2 y R1 y masas m2 y m1, respectivamente
Momento de inercia de una placa rectangular
El eje es paralelo al lado a de la placa
El eje es perpendicular la placa
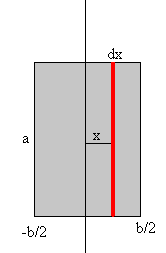
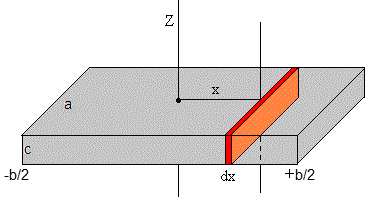
Calculamos el momento de inercia de una placa rectangular delgada de masa M, lados a y b, respecto del eje que pasa por la placa.
Tomamos un elemento diferencial de masa que dista x del eje de rotación. El elemento es un rectángulo de longitud a y de anchura dx. La masa de este rectángulo es
Calculamos el momento de inercia de una placa rectangular delgada de masa M, lados a y b, respecto de un eje perpendicular a la placa y que pasa por su centro
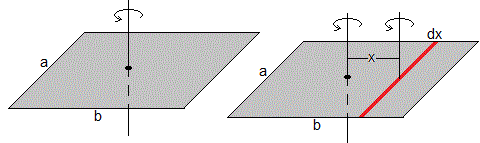
Dividimos la placa en varillas de longitud a y anchura dx, la masa de la varilla es
Aplicando el teorema de Steiner, el momento de inercia de la varilla respecto de un eje paralelo que dista x es
El momento de inercia de la placa es
Momento de inercia de un disco
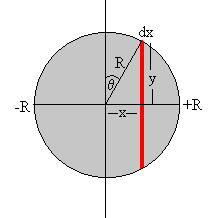
Calculamos el momento de inercia de un disco de masa M y radio R, respecto de uno de sus diámetros.
Tomamos un elemento diferencial de masa que dista x del eje de rotación. El elemento es un rectángulo de longitud 2y de anchura dx. La masa de este rectángulo es
El momento de inercia del disco es
Haciendo el cambio de variable
y=R·cosθ
x=R·sinθ
Llegamos a la integral
Momento de inercia de una esfera
Calculamos el momento de inercia de una esfera de masa M y radio R respecto de uno de sus diámetros
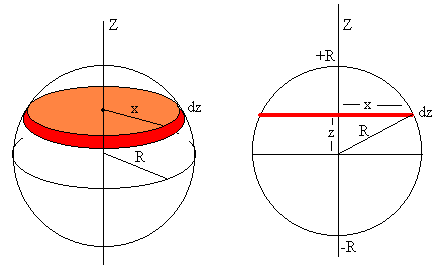
Dividimos la esfera en discos de radio x y de espesor dz. El momento de inercia de cada uno de los discos elementales es
La masa de cada uno de los discos es
El momento de inercia de la esfera, es la suma de los momentos de inercia de todos los discos elementales.
Para resolver la integral tenemos que relacionar la variable x con la z. Como vemos en la figura x2+z2=R2
Momento de inercia de una esfera hueca
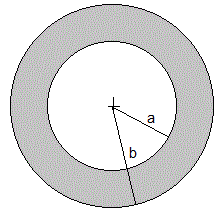
Calculamos el momento de inercia de una esfera hueca de masa M, radio interior a y radio exterior b
Si M es la masa de la esfera hueca, calculamos la masa ma de la esfera de radio a y mb de la esfera de radio b
El momento de inercia de la esfera hueca respecto de un eje que pasa por su centro es
Momento de inercia de una superficie esférica de radio R
Calculamos el momento de inercia de una placa de pequeño espesor en forma de semiesfera de radio R y masa M
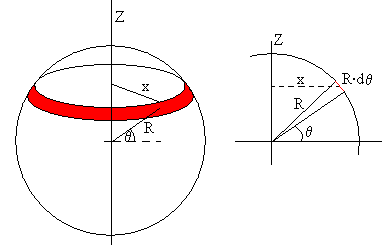
Tomamos el elemento de área mostrado en la figura, que es una franja rectangular de longitud 2πx y anchura R·dθ
Calculamos este momento de inercia a partir del momento de inercia de una esfera hueca de espesor pequeño, comparado con el radio de la esfera
Sea a=b-Δr, donde Δr<<b es el espesor. a/b=1-Δx, con Δx<<1
Utilizamos la aproximación (1-Δx)n≈1-n·Δx
Momento de inercia de un cilindro
Calculamos el momento de inercia de un cilindro de masa M, radio R y longitud L, respecto de un eje perpendicular a su generatriz y que pasa por su centro.
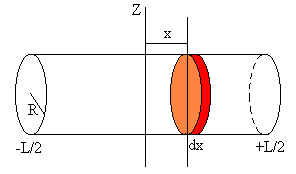
Dividimos el cilindro en discos de radio R y espesor dx. El momento de inercia de cada uno de los discos respecto de uno de sus diámetros es
Aplicando el teorema de Steiner, calculamos el momento de inercia de este disco, respecto de un eje paralelo situado a una distancia x.
El momento de inercia del cilindro es
Momento de inercia de un paralepípedo
Calculamos el momento de inercia de un paralepípedo de masa M y de lados a, b y c respecto de un eje perpendicular a una de sus caras.
Dividimos el paralepípedo en placas rectangulares de lados a y c y de espesor dx.
El momento de inercia de cada una de las placas respecto de su eje de simetría es
Aplicando el teorema de Steiner, calculamos el momento de inercia de esta placa respecto de un eje paralelo situado a una distancia x es
El momento de inercia del sólido en forma de paralepípedo es
La misma fórmula que para una placa rectangular delgada de lados a y b
Momento de inercia de un toro
Un toroide es el volumen generado al girar un círculo de radio r centrado en el punto (R,0,0) alrededor del eje Z
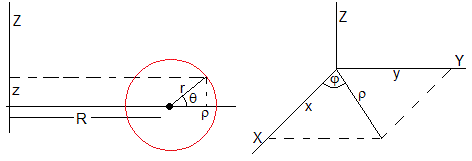
Las ecuaciones paramétricas de la superficie (toro) que contiene este volumen son
R=5; % radio del toro
r=2; % radio interior del toro
th=linspace(0,2*pi,40);
phi=linspace(0,2*pi,20);
[Phi,Th]=meshgrid(phi,th);
x=(R+r.*cos(Th)).*cos(Phi);
y=(R+r.*cos(Th)).*sin(Phi);
z=r.*sin(Th);
surf(x,y,z);
axis equal
colormap('gray')
xlabel('X');ylabel('Y');zlabel('Z');
title('Toro')
El volumen vale (2πR)(πr2)
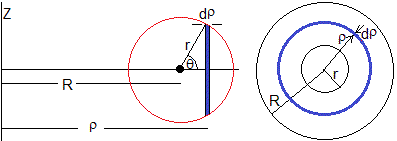
Para calcular el momento de inercia, tomamos un elemento diferencial de volumen, que contiene una masa dm
Este elemento de volumen (una capa cilíndrica) que dista ρ del eje de rotación, se obtiene al girar el ractángulo vertical sombreado en azul, alrededor del eje Z
El primer término, es el área de la base, un anillo de radios ρ y ρ+dρ y el segundo, la altura
La masa dm contenida en este elemento diferencial de volumen es
El momento de inercia respecto del eje Z del toroide es
Teniendo en cuenta el resultado de las integrales
>> syms x; >> int(sin(x)^2,x,0,pi) ans =pi/2 >> int(cos(x)^3*sin(x)^2,x,0,pi) ans =0 >> int(cos(x)*sin(x)^2,x,0,pi) ans =0 >> int(cos(x)^2*sin(x)^2,x,0,pi) ans =pi/8
La expresión final del momento de inercia de un toroide de masa M, radio medio R y radio interior r, respecto del eje Z
Sólidos de revolución
En este apartado, calculamos el centro de masa y el momento de inercia de un sólido de revolución, que se obtiene al girar una función f(x) alrededor del eje X o del eje Y
Momento de inercia respecto del eje Y
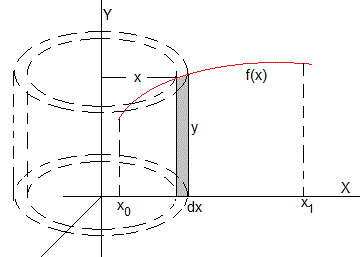
Al girar la función f(x) definida en el intervalo (x0, x1) alrededor del eje Y una vuelta, generamos un sólido de revolución.
El elemento diferencial (en color gris) comprendido entre x y x+dx de altura y=f(x) genera una capa cilíndrica cuyo volumen es
El volumen del sólido generado es
Si el sólido es homogéneo de densidad uniforme ρ, su masa el es producto de la densidad por el volumen, M=ρV
Por razones de simetría, el centro de masa del sólido estará situado en el eje Y
El centro de masa de la capa cilíndrica de radio x, espesor dx y altura y, estará situado en el eje Y a una altura y/2. Denominamos dm a la masa de dicha capa cilíndrica. El centro de masa del sólido será
El momento de inercia del sólido respecto del eje Y es
Momento de inercia de un cono macizo
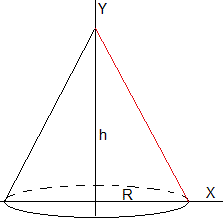
Vamos a obtener el momento de inercia de un cono de radio R, altura h y densidad ρ mediante otro procedimiento distinto
La función y=f(x) que genera el cono al girar una vuelta alrededor del eje Y es la recta y=-hx/R+h, definida en el intervalo (0,R), en color rojo en la figura.
El volumen del cono es
La posición ycm del centro de masas es
El momento de inercia del cono respecto al eje Y es
La densidad ρ es el cociente entre la masa M del cono y su volumen V. El momento de inercia es IY=3MR2/10
Momento de inercia de un sólido generado por una campana de Gauss
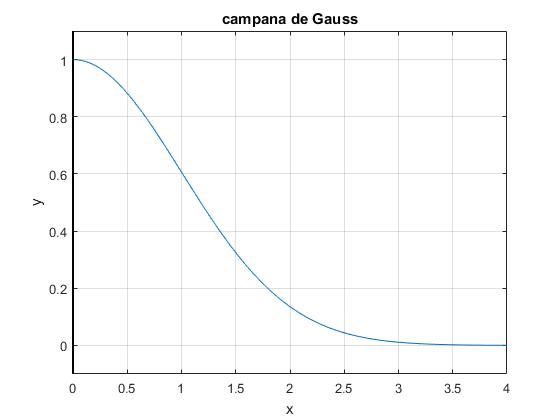
Sea f(x)=k·exp(-σx2), campana de Gauss definida en el intervalo (0, ∞)
k=1;
sigma=0.5;
f=@(x) k*exp(-sigma*x.^2);
fplot(f,[0,4])
line([0,0],[-0.1,1.1],'lineWidth',1.5,'color','k') %eje
grid on
ylim([-0.1,1.1])
xlabel('x')
ylabel('y')
title('campana de Gauss')
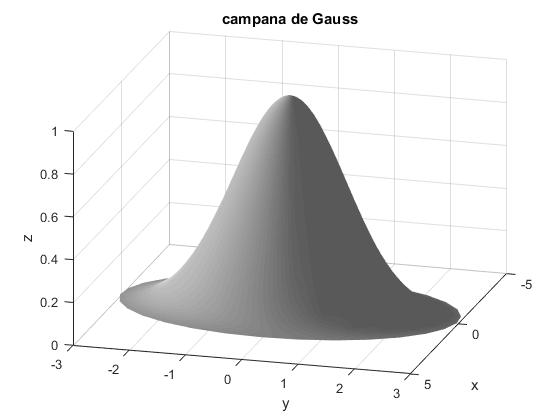
Al girar una vuelta alrededor del eje Y, (línea gruesa en la figura), genera un sólido de revolución
k=1;
sigma=0.5;
r=linspace(0,3,50);
phi=linspace(0,2*pi,30);
[r,phi]=meshgrid(r,phi);
x=r.*cos(phi);
y=r.*sin(phi);
z=k*exp(-sigma*r.^2);
surfl(x,y,z)
shading interp
colormap(gray);
xlabel('x'); ylabel('y'); zlabel('z')
title('campana de Gauss')
view(106,26)
El volumen del sólido es
La posición ycm del centro de masas es
El momento de inercia del sólido es
Integramos por partes
El resultado final es
La densidad ρ es el cociente entre la masa M del sólido y su volumen V. El momento de inercia es IY=M/σ
Momento de inercia respecto del eje X
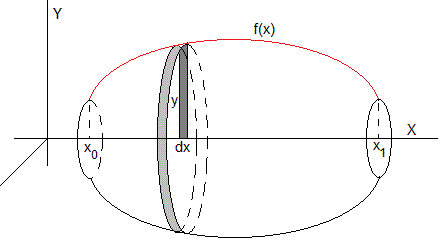
Al girar la función f(x) definida en el intervalo (x0, x1) alrededor del eje X una vuelta, en color rojo en la figura, generamos un sólido de revolución.
El elemento diferencial (en color gris oscuro) comprendido entre x y x+dx de altura y=f(x) genera un disco cuyo volumen es πy2dx. El volumen del sólido generado es
Si el sólido es homogéneo de densidad uniforme ρ, su masa es producto de la densidad por el volumen, M=ρV
Por razones de simetría, el centro de masas se encontrará en el eje X, a una distancia xcm del origen.
El centro de masa del disco de radio y, anchura dx está situado a una distancia x del origen. El centro de masa del sólido será
El momento de inercia de un disco de masa dm=ρπy2·dx respecto del eje X, perpendicular al plano del disco, que pasa por su centro es dm·y2/2
El momento de inercia del sólido respecto del eje X es
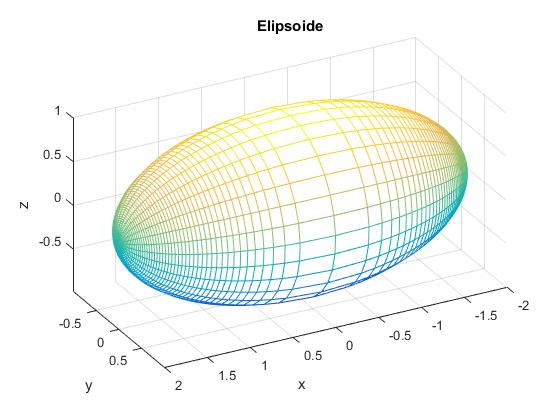
Momento de inercia de un elipsoide de revolución
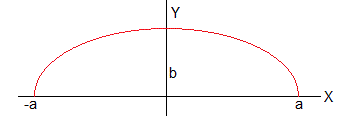
Al girar la elipse de semiejes a y b alrededor del eje X, obtenemos un elipsoide de revolución
La ecuación de una elipse es
La función y=f(x) definida en el intervalo (-a, a) que genera el elipsoide al girar una vuelta alrededor del eje X, es
a=2;
b=1;
r=linspace(0,b,50);
phi=linspace(0,2*pi,30);
[r,phi]=meshgrid(r,phi);
z=r.*cos(phi);
y=r.*sin(phi);
x=a*sqrt(b^2-r.^2)/b;
z=[z,z];
y=[y,y];
x=[x,-x];
mesh(x,y,z)
axis equal
xlabel('x'); ylabel('y'); zlabel('z')
title('Elipsoide')
view(152,26)
El volumen del elipsoide es
Por razones de simetría, el centro de masa del elipsoide de revolución está situado en el origen, pero podríamos estar interesados en conocer la posición xcm del centro de masa de la mitad (x≥0) del sólido
El momento de inercia del sólido respecto del eje X es
La densidad ρ es el cociente entre la masa M del sólido y su volumen V, el momento de inercia es IX=2Mb2/5
Cuando b=a, obtenemos los resultados para una esfera maciza de radio R
Referencias
Para el apartado 'Sólidos de revolución'
Rodolfo A Diaz, William J Herrera, R Martinez. Moments of inertia for solids of revolution and variational methods. Eur. J. Phys. 27 (2006) pp. 183-192

