Apuntar un cañón para dar en el blanco

Apuntar un cañón para dar en el blanco.

En el programa interactivo, al pulsar sobre el botón Nuevo aparece un terreno cuyo perfil está trazado por una función cuyos coeficientes son números aleatorios. Sobre dicho terreno se sitúa el blanco también de forma aleatoria.

Antes de proceder a resolver numéricamente el problema, se usará el programa como un juego: dar en el blanco en el menor número de intentos posibles. Esto constituye una primera aproximación a la resolución del problema, ya que nos proporciona un conocimiento intuitivo de la situación física, permitiéndonos determinar el ángulo aproximado de tiro que acierta en el blanco. Además, se comprobará que existen dos posibles soluciones, dos ángulos de tiro que dan en el blanco. A veces, por el perfil del terreno, sólo es posible el ángulo que corresponde a la trayectoria más alta.

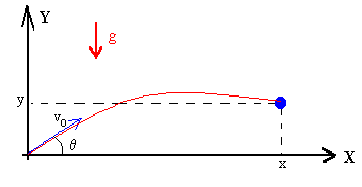
El movimiento del proyectil es la composición de dos movimientos, uniforme a lo largo del eje X, y uniformemente acelerado a lo largo del eje Y.

Conocidas las coordenadas del blanco x e y, y la velocidad de disparo v₀, se despejará el ángulo de tiro θ.

Las componentes de la velocidad inicial son

$\begin{array}{l} v_{0 x} = v_{0} \cos θ \\ v_{0 y} = v_{0} \sin θ \end{array}$

Las ecuaciones del movimiento del proyectil son

$\begin{array}{l} x = v_{0} \cos θ t \\ y = y_{0} + v_{0} \sin θ t - \frac{1}{2} g t^{2} \end{array}$

Conocida la posición (x, y) del blanco, tenemos un sistema de dos ecuaciones con dos incógnitas t y θ. Eliminando t y empleando la relación trigonométrica

$\frac{1}{\cos^{2} θ} = 1 + \tan^{2} θ$

nos queda una ecuación de segundo grado en tanθ

$(\frac{g x^{2}}{2 v_{0}^{2}}) \tan^{2} θ - x \tan θ + (\frac{g x^{2}}{2 v_{0}^{2}} + y) = 0$

Ejemplo

El programa interactivo nos proporciona los datos de la posición del blanco y la velocidad de disparo.

Posición del blanco x=159.7, y=151.7 m
Velocidad de disparo v₀=89.9 m/s

Con estos datos, la ecuación de segundo grado se escribe

13.46 tan²θ -159.7 tanθ +167.16=0

Las soluciones son

tanθ =9.15, θ =83.8º
tanθ =1.18, θ =49.8º

Actividades

Se puede utilizar el programa como un juego, para tratar de acertar en el blanco en el menor número de intentos.

Se recomienda resolver al menos una situación numéricamente, introduciendo uno de los dos ángulos calculados en el control titulado Angulo de tiro para acertar al primer intento, comprobándose de este modo que la solución es correcta.

Se pulsa el botón Nuevo para que el programa dibuje el perfil del terreno y sitúe aleatoriamente el blanco. La velocidad de disparo v₀ es un número aleatorio dentro de ciertos límites.
Se introduce el ángulo de tiro θ en el control titulado Angulo de tiro
Se pulsa el botón titulado ►
Si no ha dado en el blanco, se vuelve a introducir un nuevo ángulo de tiro y se pulsa el botón titulado ►.

Angulo de tiro:

Dos posibles ángulos de tiro para dar en el blanco

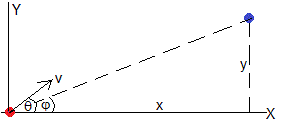
Un problema típico de cinemática tiene el siguiente enunciado. Disponemos de un cañón que dispara proyectiles con velocidad v₀. Calcular el ángulo o los ángulos de tiro θ para apuntar a un blanco situado a una distancia horizontal x y altura y.

La ecuación de la trayectoria del proyectil es

${\begin{cases} x = v \cos θ \cdot t \\ y = v \sin θ \cdot t - \frac{1}{2} g t^{2} \end{cases}$

Eliminamos el tiempo t y despejamos el ángulo de tiro θ

$\begin{array}{l} y = x \tan θ - \frac{1}{2} g \frac{x^{2}}{v_{0}^{2} \cos^{2} θ} = x \tan θ - \frac{1}{2} g \frac{x^{2}}{v_{0}^{2}} (1 + \tan^{2} θ) \\ \tan^{2} θ - 2 \frac{v_{0}^{2}}{g x} \tan θ + 1 + \frac{2 v_{0}^{2}}{g x^{2}} y = 0 \\ \tan θ = \frac{v_{0}^{2}}{g x} \pm \sqrt{{(\frac{v_{0}^{2}}{g x})}^{2} - 1 - \frac{2 v_{0}^{2}}{g x^{2}} y} \end{array}$

Hay dos posibles ángulos de tiro que apuntan al blanco

Ejemplo

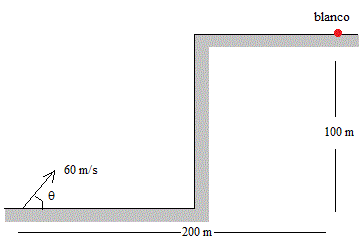
Calcular el ángulo de tiro con que se ha de apuntar un cañón para que dé en el blanco situado a 200 m de distancia horizontal y 100 m de altitud sobre el cañón, sabiendo que la velocidad de disparo es de 60 m/s. (Tómese g=10 m/s²)

${\begin{cases} a_{x} = 0 \\ a_{y} = - 10 \end{cases} {\begin{cases} v_{x} = 60 \cdot \cos θ \\ v_{y} = 60 \cdot \sin θ + (- 10) t \end{cases} {\begin{cases} x = 60 \cdot \cos θ \cdot t \\ y = 60 \cdot \sin θ t + \frac{1}{2} (- 10) t^{2} \end{cases}$

Punto de impacto: x=200 m, y=100 m. Para calcular los ángulos de tiro θ despejamos el tiempo t en la primera ecuación y la sustituímos en la segunda, quedando una ecuación de segundo grado en tanθ.

$\begin{array}{l} t = \frac{10}{3 \cdot \cos θ} 1 = 2 \cdot \sin θ \frac{1}{\cos θ} - 5 \frac{1}{9 \cdots \cos^{2} θ} \\ \frac{1}{\cos^{2} θ} = 1 + \tan^{2} θ \\ \frac{5}{9} \tan^{2} θ - 2 \tan θ + \frac{14}{9} = 0 {\begin{cases} θ_{1} = 67.9 º \\ θ_{2} = 48.7 º \end{cases} \end{array}$

Representamos las trayectorias

v0=60; %velocidad de disparo
x=200; %posición del blanco
y=100; 
g=10; %aceleración de la gravedad
dis=sqrt((v0^2/(g*x))^2-1-2*v0^2*y/(g*x^2)); 
th_1=atan(v0^2/(g*x)+dis); %ángulos
th_2=atan(v0^2/(g*x)-dis);
disp([th_1*180/pi, th_2*180/pi])
t1=x/(v0*cos(th_1));%tiempos
t2=x/(v0*cos(th_2));

hold on
fill([100,100,250 250],[0,100,100,0],'g') %terreno
%trayectorias
fplot(@(t) v0*cos(th_1)*t, @(t) v0*sin(th_1)*t-g*t.^2/2,[0,t1],'color','b')
t=linspace(0,t2,100);
x=v0*cos(th_2)*t;
y=v0*sin(th_2)*t-g*t.^2/2;
plot(x(x<=100),y(x<=100),'r') %hasta que choca con la pared
hold off
xlabel('x (m)')
ylabel('y (m)')
title('Tiro parabólico')

Los ángulos de tiro son

  67.9050   48.6600

El impacto en el blanco se consigue apuntando más alto

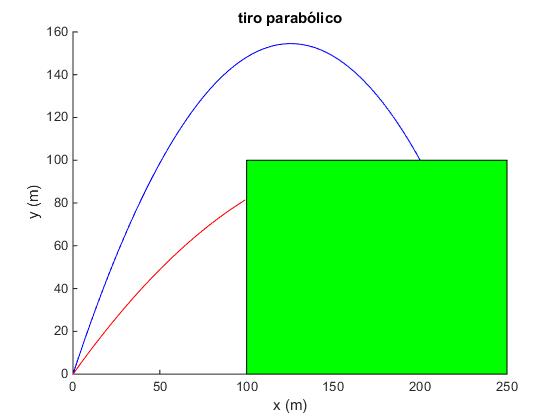
Calculamos la altura y del proyectil en la posición x=100, para el ángulo de tiro θ₁=67.90° y para el ángulo θ₂=48.66°

>> t=100/(v0*cos(th_1));
>> y=v0*sin(th_1)*t-g*t^2/2
y =  148.1662
>> t=100/(v0*cos(th_2));
>> y=v0*sin(th_2)*t-g*t^2/2
y =   81.8338

En el primer caso, θ₁=67.90°, la altura del proyectil es y=148.2 m, mayor que la del obstáculo (pared). En el segundo, θ₂=48.66°, la altura del proyectil es y=81.8 m, menor que la altura de la pared

Velocidad de disparo para un único ángulo de tiro

Los dos ángulos θ₁ y θ₂ son iguales cuando el discriminante es nulo. Esto ocurre para la velocidad de disparo v₀ tal que

$\begin{array}{l} {(\frac{v_{0}^{2}}{g x})}^{2} - 1 - \frac{2 v_{0}^{2}}{g x^{2}} y = 0 \\ v_{0}^{4} - 2 g y v_{0}^{2} - g^{2} x^{2} = 0 \\ v_{0}^{2} = \frac{2 g y \pm \sqrt{4 g^{2} y^{2} + 4 g^{2} x^{2}}}{2} \\ v_{0}^{2} = g (y + r), r = \sqrt{x^{2} + y^{2}} \end{array}$

Solamente es posible la raíz positiva

El ángulo de tiro es

$\tan θ = \frac{v_{0}^{2}}{g x} = \frac{r + y}{x} = \frac{r}{x} + \frac{y}{x} = \frac{1}{\cos φ} + \tan φ, \tan φ = \frac{y}{x}$

Demostramos más adelante v₀ es mínima y que la relación entre el ángulo de tiro θ y el ángulo φ del blanco (véase la primera figura de este apartado) es

$θ = \frac{φ}{2} + \frac{π}{4}$

Velocidad de disparo mínima

Un problema algo más difícil consiste, en calcular la velocidad de disparo v₀ mínima y el ángulo θ de tiro para que el proyectil impacte en un blanco dado

Despejamos la velocidad v₀ de disparo de la ecuación de la trayectoria

$\begin{array}{l} {\begin{cases} x = v_{0} \cos θ \cdot t \\ y = v_{0} \sin θ \cdot t - \frac{1}{2} g t^{2} \end{cases} \\ v_{0}^{2} = \frac{x^{2}}{\cos^{2} θ} \frac{g}{2 (x \tan θ - y)} \end{array}$

Teniendo en cuenta la identidad, 1+tan²θ=1/cos²θ, calculamos el extremo de de la función

$f (θ) = \frac{1 + \tan^{2} θ}{(x \tan θ - y)}$

Para que la velocidad de disparo v₀ sea mínima, derivamos la función f(θ) respecto de θ e igualamos a cero, obteniendo la ecuación

$\begin{array}{l} 2 \tan θ \frac{1}{\cos^{2} θ} (x \tan θ - y) - \frac{x}{\cos^{2} θ} (1 + \tan^{2} θ) = 0 \\ \tan^{2} θ - 2 \frac{y}{x} \tan θ - 1 = 0 \end{array}$

Sea

$\tan φ = \frac{y}{x}, r = \sqrt{x^{2} + y^{2}}$

La raíz positiva de la ecuación de segundo grado es

$\tan θ = \tan φ + \sqrt{1 + \tan^{2} φ} = \tan φ + \frac{1}{\cos φ} = \frac{1 + \sin φ}{\cos φ}$

Teniendo en cuenta la relación trigonométrica

$\tan θ = \frac{\sin θ}{\cos θ} = \frac{\sin^{2} θ}{\cos θ \cdot \sin θ} = \frac{1 - \cos (2 θ)}{\sin (2 θ)} = \frac{1 + \sin (2 θ - \frac{π}{2})}{\cos (2 θ - \frac{π}{2})}$

Identificamos el ángulo φ=2θ-π/2. El ángulo de tiro es

$θ = \frac{φ}{2} + \frac{π}{4}, \tan φ = \frac{y}{x}$

Teniendo en cuenta que

$\begin{array}{l} \tan θ = \tan φ + \sqrt{1 + \tan^{2} φ} = \frac{y}{x} + \sqrt{1 + \frac{y^{2}}{x^{2}} =} \frac{y}{x} + \frac{r}{x} = \frac{y + r}{x} \\ \cos^{2} θ = \frac{1}{1 + \tan^{2} θ} = \frac{x^{2}}{2 r (r + y)} \end{array}$

La velocidad v₀ de disparo mínima es

$\begin{array}{l} v_{0}^{2} = \frac{x^{2}}{\cos^{2} θ} \frac{g}{2 (x \tan θ - y)} = g (r + y) \\ v_{0} = \sqrt{g (r + y)} \end{array}$

Representamos, las dos trayectorias (color rojo y azul) con la velocidad de disparo v₀=60 m/s, y la trayectoria con la velocidad de disparo mínima (color negro)

v0=60; %velocidad de disparo
x=200; %posición del blanco
y=100; 
g=10; %aceleración de la gravedad
dis=sqrt((v0^2/(g*x))^2-1-2*v0^2*y/(g*x^2)); 
th_1=atan(v0^2/(g*x)+dis); %ángulos
th_2=atan(v0^2/(g*x)-dis);
disp([th_1*180/pi, th_2*180/pi])
t1=x/(v0*cos(th_1));%tiempos de vuelo
t2=x/(v0*cos(th_2));
%mínimo
vm=sqrt(g*(sqrt(x^2+y^2)+y)); %velocidad de disparo
th_m=atan(y/x)/2+pi/4; %ángulo de tiro
tm=x/(vm*cos(th_m)); %tiempo de vuelo
hold on
%trayectorias
fplot(@(t) v0*cos(th_1)*t, @(t) v0*sin(th_1)*t-g*t.^2/2,[0,t1],'color','b')
fplot(@(t) v0*cos(th_2)*t, @(t) v0*sin(th_2)*t-g*t.^2/2,[0,t2],'color','r')
fplot(@(t) vm*cos(th_m)*t, @(t) vm*sin(th_m)*t-g*t.^2/2,[0,tm],'color','k')
hold off
grid on
xlabel('x (m)')
ylabel('y (m)')
legend(num2str(th_1*180/pi), num2str(th_2*180/pi),
num2str(th_m*180/pi),'location','best')
title('Tiro parabólico')

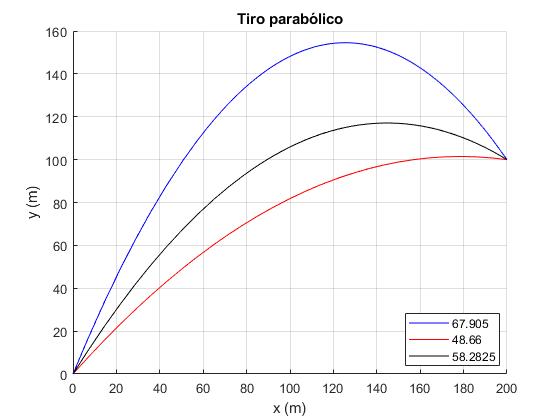
La velocidad de disparo mínima y el ángulo de tiro, son

>> vm
vm =   56.8864
>> th_m*180/pi
ans =   58.2825

Referencias

Carl E. Mungan. Optimizing the Launch of a Projectile to Hit a Target. The Physics Teacher, Vol.55, December 2017, pp. 528-529

Este artículo está disponible en la dirección: https://www.usna.edu/Users/physics/mungan/Publications/Publications.php#fndtn-panel120162017