Campo eléctrico

Cuando un dieléctrico no polar se coloca en un campo eléctrico las cargas positivas y negativas de las moléculas se desplazan unas respecto de las otras, las moléculas se polarizan. El momento dipolar inducido por unidad de volumen $\overrightarrow{P}$, se llama polarización eléctrica

${\displaystyle \begin{array}{l}{\sigma }_b=\overrightarrow{P}·\widehat{n}\\ {\rho }_b=-\overrightarrow{\nabla }·\overrightarrow{P}\end{array}}$

donde σ_b, C/m², es la densidad superficial y ρ_b, C/m³, la densidad (en volumen) de carga ligada

La ley de Gauss se puede expresar

${\displaystyle \overrightarrow{\nabla }·\overrightarrow{E}=\frac{{\rho }_t}{{\epsilon }_0}}$

donde la densidad de carga total ρ_t es la suma de la densidad de carga libre ρ_f y la densidad de carga ligada ρ_b

Se define el vector desplazamiento eléctrico

${\displaystyle \overrightarrow{D}={\epsilon }_0\overrightarrow{E}+\overrightarrow{P}={\epsilon }_0{\epsilon }_r\overrightarrow{E}=\epsilon \overrightarrow{E}}$

donde ε_r es la permitividad relativa o constante diléctrica y ε es la permitividad del medio. El vector $\overrightarrow{D}$ está relacionado con la densidad de carga libre

${\displaystyle \begin{array}{l}\overrightarrow{\nabla }·\overrightarrow{D}={\rho }_f\\ {\displaystyle \underset{S}{\int }\overrightarrow{D}·\overrightarrow{dS}}={\displaystyle \underset{V}{\int }{\rho }_f·dV}\end{array}}$

Superficie de separación entre dos medios

En la separación de dos medios diferentes, el potencial V debe ser continuo, ya que una discontinuidad implicaría un campo eléctrico infinito. El potencial debe anularse en el infinito si las distribuciones de carga tiene extensión finita y debe ser constante en un conductor si las cargas eléctricas están en reposo.

• Componente normal del desplazamiento eléctrico $\overrightarrow{D}$



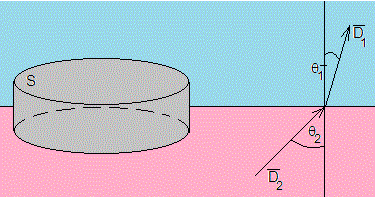
Consideremos una superficie cilíndrica de base S y de altura muy pequeña entre los dos medios.

El flujo de $\overrightarrow{D}$ solamente se produce a través de las bases, ya que el área lateral es arbitrariamente pequeña.

Si en la superficie de separación existe una densidad superficial de carga libre σ_f, el flujo del vector $\overrightarrow{D}$ a través de la superficie cilíndrica es

${\displaystyle \begin{array}{l}{D}_1\cos {\theta }_1·S-D_2\cos {\theta }_2·S={\sigma }_{f}S\\ D_{n1}-D_{n2}={\sigma }_f\end{array}}$

D_n1 y D_n2 son las componentes normales de $\overrightarrow{D}$

Si en la separación de dos medios dieléctricos, la densidad superficie la de carga libre es σ_f es nula, en estas condiciones la componente normal de $\overrightarrow{D}$ es continua al cruzar la superficie de separación.

Si la superficie separa un conductor de un dieléctrico, el campo eléctrico es constante en el conductor, y D_n=σ_f en el dieléctrico, siendo σ_f la densidad de carga libre en la superficie del conductor.

• Componente tangencial de la intensidad del campo eléctrico $\overrightarrow{E}$



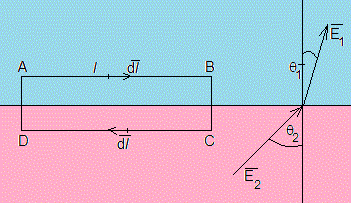
El campo eléctrico $\overrightarrow{E}$ es conservativo. Tomamos un camino cerrado rectangular ABCD, los lados AB y CD tienen longitud l, los lados AD y BC tiene una longitud arbitrariamente pequeña. La circulación

${\displaystyle \begin{array}{l}{\displaystyle \oint \overrightarrow{E}·\overrightarrow{dl}}={\displaystyle \underset{A}{\overset{B}{\int }}\overrightarrow{E}·\overrightarrow{dl}}+{\displaystyle \underset{B}{\overset{C}{\int }}\overrightarrow{E}·\overrightarrow{dl}}+{\displaystyle \underset{C}{\overset{D}{\int }}\overrightarrow{E}·\overrightarrow{dl}}+{\displaystyle \underset{D}{\overset{A}{\int }}\overrightarrow{E}·\overrightarrow{dl}}=0\\ E_1\sin {\theta }_1·l+0-E_2\sin {\theta }_2·l+0=0\\ E_{t1}=E_{t2}\end{array}}$

La componente tangencial del campo eléctrico es continua al cruzar la superficie de separación entre dos medios.

Si la separación es la de un conductor y un dieléctrico, entonces $\overrightarrow{E}=0$ en el conductor y E_t=0 en el dieléctrico. El campo eléctrico el perpendicular a la superficie del conductor.

De las dos relaciones se deduce que

${\displaystyle \begin{array}{l}{D}_1\cos {\theta }_1=D_2\cos {\theta }_2\\ \{\begin{array}{l}{\epsilon }_{r1}{\epsilon }_0{E}_1\cos {\theta }_1={\epsilon }_{r2}{\epsilon }_0{E}_2\cos {\theta }_2\\ E_1\sin {\theta }_1=E_2\sin {\theta }_2\end{array}\end{array}}$

Dividiendo la segunda entre la primera

${\displaystyle \begin{array}{l}\frac{1}{{\epsilon }_{r1}}\tan {\theta }_1=\frac{1}{{\epsilon }_{r2}}\tan {\theta }_2\\ \frac{\tan {\theta }_1}{\tan {\theta }_2}=\frac{{\epsilon }_{r1}}{{\epsilon }_{r2}}\end{array}}$

El ángulo mayor con la normal ocurre en el medio de permitividad relativa mayor

Campo magnético

La imanación $\overrightarrow{M}$ de los materiales magnéticos se corresponde con la polarización $\overrightarrow{P}$ de los materiales dieléctricos.

Según el modelo de Ampère, la imanación produce una densidad de corriente equivalente en la superficie $\overrightarrow{{\lambda }_e}$ y una densidad de corriente equivalente en el volumen $\overrightarrow{J_e}$ donde

${\displaystyle \begin{array}{l}\overrightarrow{{\lambda }_e}=\overrightarrow{M}\times \widehat{n}\\ \overrightarrow{J_e}=\overrightarrow{\nabla }\times \overrightarrow{M}\end{array}}$

La inducción magnética $\overrightarrow{B}$ se puede calcular tanto dentro como fuera del material magnético tratando las corrientes equivalentes como si fueran corrientes reales de conducción circulando en el vacío.

La intensidad del campo magnético $\overrightarrow{H}$ está relacionado con $\overrightarrow{B}$ y $\overrightarrow{M}$ del siguiente modo

${\displaystyle \begin{array}{l}\overrightarrow{B}={\mu }_0\left(\overrightarrow{H}+\overrightarrow{M}\right)\\ \overrightarrow{B}={\mu }_0{\mu }_r\overrightarrow{H}=\mu \overrightarrow{H}\end{array}}$

donde μ_r es la permeabilidad relativa y μ la permeabilidad

La ley de Ampére se escribe

${\displaystyle \begin{array}{l}\overrightarrow{\nabla }\times \overrightarrow{H}=\overrightarrow{J_f}\\ {\displaystyle \oint \overrightarrow{H}·\overrightarrow{dl}}=i_f\end{array}}$

donde i_f es la intensidad de la corriente de cargas libres que atraviesa el camino cerrado

La ley de Gauss para el campo magnético es

${\displaystyle {\displaystyle \underset{S}{\int }\overrightarrow{B}·\overrightarrow{dS}}=0}$

Superficie de separación entre dos medios

• Componente normal del campo magnético $\overrightarrow{B}$



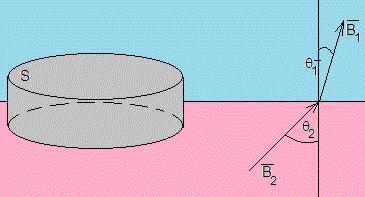
Consideremos una superficie cilíndrica de base S y de altura muy pequeña entre los dos medios.

El flujo de $\overrightarrow{B}$ solamente se produce a través de las bases, ya que el área lateral es arbitrariamente pequeña.

${\displaystyle \begin{array}{l}{B}_1\cos {\theta }_1·S-B_2\cos {\theta }_2·S=0\\ B_{n1}=B_{n2}\end{array}}$

La componente normal de $\overrightarrow{B}$ es continua al atravesar la superficie de separación

• Componente tangencial de $\overrightarrow{H}$



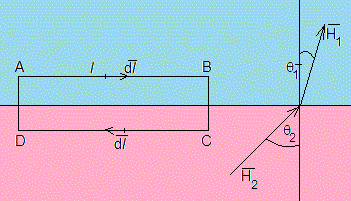
Tomamos un camino cerrado rectangular ABCD, los lados AB y CD tienen longitud l, los lados AD y BC tiene una longitud arbitrariamente pequeña. La circulación

${\displaystyle {\displaystyle \oint \overrightarrow{H}·\overrightarrow{dl}}=i_f}$

Si no hay corrientes que atraviesen el camino cerrado ABCD

${\displaystyle \begin{array}{l}{\displaystyle \underset{A}{\overset{B}{\int }}\overrightarrow{H}·\overrightarrow{dl}}+{\displaystyle \underset{B}{\overset{C}{\int }}H·\overrightarrow{dl}}+{\displaystyle \underset{C}{\overset{D}{\int }}\overrightarrow{H}·\overrightarrow{dl}}+{\displaystyle \underset{D}{\overset{A}{\int }}\overrightarrow{H}·\overrightarrow{dl}}=0\\ H_1\sin {\theta }_1·l+0-H_2\sin {\theta }_2·l+0=0\\ H_{t1}=H_{t2}\end{array}}$

La componente tangencial de $\overrightarrow{H}$ es continua al cruzar la superficie de separación entre dos medios.

De las dos relaciones se deduce

${\displaystyle \begin{array}{l}{B}_1\cos {\theta }_1=B_2\cos {\theta }_2\\ \{\begin{array}{l}{\mu }_{r1}{\mu }_0{H}_1\cos {\theta }_1={\mu }_{r2}{\mu }_0{H}_2\cos {\theta }_2\\ H_1\sin {\theta }_1=H_2\sin {\theta }_2\end{array}\end{array}}$

Dividiendo la segunda entre la primera

${\displaystyle \begin{array}{l}\frac{1}{{\mu }_{r1}}\tan {\theta }_1=\frac{1}{{\mu }_{r2}}\tan {\theta }_2\\ \frac{\tan {\theta }_1}{\tan {\theta }_2}=\frac{{\mu }_{r1}}{{\mu }_{r2}}\end{array}}$

El ángulo mayor con la normal ocurre en el medio de permeabilidad relativa mayor

Ecuaciones de Maxwell. Ondas electromagnéticas

Las ecuaciones de Maxwell en forma diferencial e integral son

Otra forma alternativa a la cuarta ecuación de Maxwell que se utilizará en la dedución de la ecuación de las ondas electromagnéticas es

${\displaystyle \begin{array}{l}\overrightarrow{\nabla }\times \overrightarrow{H}=\overrightarrow{J_f}+\frac{\partial \overrightarrow{D}}{\partial t}\\ \overrightarrow{\nabla }\times \overrightarrow{B}=\mu \overrightarrow{J_f}+\mu \epsilon \frac{\partial \overrightarrow{E}}{\partial t}\end{array}}$

Para obtener la segunda, se multiplica la primera por μ y se utiliza las relaciones entre los vectores, $\overrightarrow{D}=\epsilon \overrightarrow{E},\overrightarrow{B}=\mu \overrightarrow{H}$

Densidad de carga y corrientes

${\displaystyle \begin{array}{l}{\rho }_t={\rho }_f+{\rho }_b\\ \overrightarrow{J_m}=\overrightarrow{J_f}+\frac{\partial \overrightarrow{P}}{\partial t}+\overrightarrow{\nabla }\times \overrightarrow{M}\end{array}}$

Nomenclatura

• ρ_f, es la densidad de carga libre
• ${\rho }_b=-\overrightarrow{\nabla }·\overrightarrow{P}$, es la densidad de carga ligada
• $\overrightarrow{J_f}$, es la densidad de corriente de cargas libres
• $\frac{\partial \overrightarrow{P}}{\partial t}$, es la densidad de corriente de polarización
• $\overrightarrow{\nabla }\times \overrightarrow{M}$, es la densidad de corriente equivalente en la materia imanada
• ε, es la permitividad del material, ε₀=8.8542·10^-12 F/m es la del vacío
• μ, es la permeabilidad, μ₀=4π·10^-7 H/m es la del vacío

Ondas electromagnéticas

En este apartado utilizamos la propiedad

${\displaystyle \overrightarrow{\nabla }\times \overrightarrow{\nabla }\times \overrightarrow{A}=-{\nabla }^2\overrightarrow{A}+\overrightarrow{\nabla }\left(\overrightarrow{\nabla }·\overrightarrow{A}\right)}$

• Campo eléctrico

Partimos de la ley de Faraday

${\displaystyle \overrightarrow{\nabla }\times \overrightarrow{E}+\frac{\partial \overrightarrow{B}}{\partial t}=0}$

Aplicamos a ambos miembros el operador $\overrightarrow{\nabla }\times$

Obtenemos

${\displaystyle \begin{array}{l}{\nabla }^2\overrightarrow{E}-\overrightarrow{\nabla }\left(\overrightarrow{\nabla }·\overrightarrow{E}\right)=\frac{\partial }{\partial t}\overrightarrow{\nabla }\times \overrightarrow{B}\\ {\nabla }^2\overrightarrow{E}-\overrightarrow{\nabla }\left(\overrightarrow{\nabla }·\overrightarrow{E}\right)=\frac{\partial }{\partial t}\overrightarrow{\nabla }\times \overrightarrow{B}\\ {\nabla }^2\overrightarrow{E}-\frac{1}{\epsilon }\overrightarrow{\nabla }{\rho }_f=\frac{\partial }{\partial t}\left(\mu \overrightarrow{J_f}+\epsilon \mu \frac{\partial \overrightarrow{E}}{\partial t}\right)\\ {\nabla }^2\overrightarrow{E}-\epsilon \mu \frac{{\partial }^2\overrightarrow{E}}{\partial t^2}=\frac{1}{\epsilon }\overrightarrow{\nabla }{\rho }_f+\mu \frac{\partial \overrightarrow{J_f}}{\partial t}\end{array}}$

En las regiones en las que se anulan ρ_f y $\overrightarrow{J_f}$ , no hay densidad de carga libre ni corrientes de cargas libres seobtiene la ecuación de ondas homogénea

${\displaystyle {\nabla }^2\overrightarrow{E}-\epsilon \mu \frac{{\partial }^2\overrightarrow{E}}{\partial t^2}=0}$

• Campo magnético

Partimos de la ley de Ampère-Maxwell

${\displaystyle \overrightarrow{\nabla }\times \overrightarrow{B}=\mu \overrightarrow{J_f}+\epsilon \mu \frac{\partial \overrightarrow{E}}{\partial t}}$

Aplicamos a ambos miembros el operador $\overrightarrow{\nabla }\times$

Obtenemos

${\displaystyle \begin{array}{l}-{\nabla }^2\overrightarrow{B}-\overrightarrow{\nabla }\left(\overrightarrow{\nabla }·\overrightarrow{B}\right)=\mu \overrightarrow{\nabla }\times \overrightarrow{J_f}+\epsilon \mu \frac{\partial }{\partial t}\overrightarrow{\nabla }\times \overrightarrow{E}\\ -{\nabla }^2\overrightarrow{B}=\mu \overrightarrow{\nabla }\times \overrightarrow{J_f}-\epsilon \mu \frac{{\partial }^2\overrightarrow{B}}{\partial t^2}\\ {\nabla }^2\overrightarrow{B}-\epsilon \mu \frac{{\partial }^2\overrightarrow{B}}{\partial t^2}=-\mu \overrightarrow{\nabla }\times \overrightarrow{J_f}\end{array}}$

En la región en la que no hay corrientes $\overrightarrow{J_f}$, se cumple la ecuación de ondas homogénea

${\displaystyle {\nabla }^2\overrightarrow{B}-\epsilon \mu \frac{{\partial }^2\overrightarrow{B}}{\partial t^2}=0}$

Estudiaremos la propagación de ondas electromagnéticas en medios homogéneos, isótropos, lineales y estacionarios. No conductores y no magnéticos

• Un medio es homogéneo si sus propiedades no varían con la posición

• Un medio es isótropo, si para un punto dado, sus propiedades son las mismas en todas las direcciones

• Es lineal si la permitividad ε y la permeabilidad μ son constantes e independientes de $\overrightarrow{E}$ y $\overrightarrow{H}$

• Un sistema se dice estacionario, cuando las variables que definen su comportamiento no cambian con el tiempo

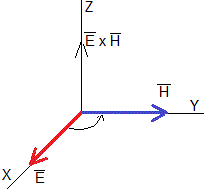
El caso más sencillo es el de una onda plana que se propaga a lo largo del eje Z. El campo eléctrico $\overrightarrow{E}$ es independiente de x e y

${\displaystyle \overrightarrow{E}=E_0\exp \left(i\left(\omega t-kz\right)\right)\widehat{i}}$

Se dice que es una onda electromagnética linealmente polarizada por que el campo eléctrico oscila en el eje X y el campo magnético oscila en el eje Y

Introduciendo en la ecuacuión de onda para el campo eléctrico

${\displaystyle \begin{array}{l}(-ik)(-ik)E_0\exp \left(i\left(\omega t-kz\right)\right)\widehat{i}-\epsilon \mu (i\omega )(i\omega )E_0\exp \left(i\left(\omega t-kz\right)\right)\widehat{i}=0\\ -k^2+\epsilon \mu {\omega }^2=0\\ v=\frac{\omega }{k}=\frac{1}{\sqrt{\epsilon \mu }}=\frac{c}{\sqrt{{\epsilon }_r{\mu }_r}}\end{array}}$

v=ω/k se denomina velocidad de fase

Se define índice de refracción n=c/v el cociente entre la velocidad de la luz en el vacío y la velocidad de la luz en un medio

${\displaystyle n=\frac{c}{v}=\sqrt{{\epsilon }_r{\mu }_r}\approx \sqrt{{\epsilon }_r}}$

Las ondas electromagnéticas constan de una campo eléctrico y un campo magnético perpendiculares entre sí y a la dirección de propagación $\overrightarrow{E}\times \overrightarrow{H}$, si el campo eléctrico tiene la dirección del eje X, el campo magnético tiene la dirección del eje Y,

${\displaystyle \overrightarrow{H}=H_0\exp \left(i\left(\omega t-kz\right)\right)\widehat{j}=H_0\exp \left(i\omega \left(t-\frac{z}{v}\right)\right)\widehat{j}}$

como vamos a comprobar utilizando la ley de Faraday

${\displaystyle \begin{array}{l}\overrightarrow{\nabla }\times \overrightarrow{E}+\mu \frac{\partial \overrightarrow{H}}{\partial t}=0\\ \left|\begin{array}{ccc}\widehat{i}& \widehat{j}& \widehat{k}\\ \frac{\partial }{\partial x}& \frac{\partial }{\partial y}& \frac{\partial }{\partial z}\\ E_0\exp \left(i\left(\omega t-kz\right)\right)& 0& 0\end{array}\right|+\mu \frac{\partial \overrightarrow{H}}{\partial t}=0\\ -ki{E}_0\widehat{j}+\mu i\omega H_0\widehat{j}=0\\ H_0=E_0\frac{k}{\omega \mu },H_0=\sqrt{\frac{\epsilon }{\mu }}{E}_0\end{array}}$

Esta es la relación entre las amplitudes de la onda eléctrica E₀ y la onda magnética H₀

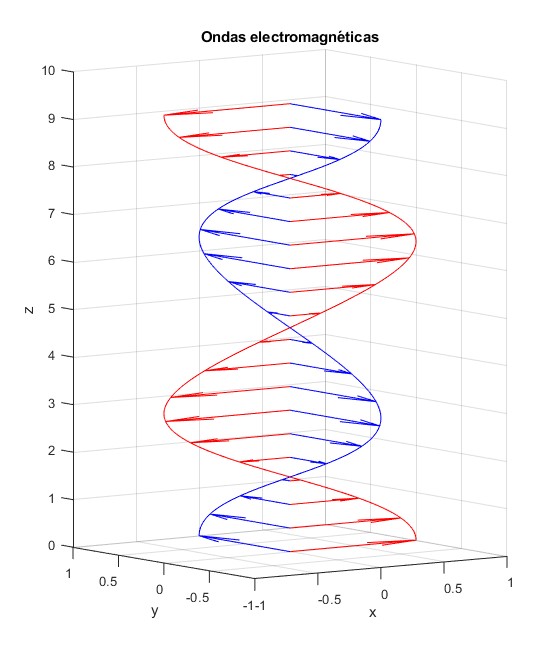
Representamos la onda eléctrica y la onda magnética con las mismas amplitudes. Las flechas indican el vector campo eléctrico $\overrightarrow{E}$ y el vector campo magnético $\overrightarrow{H}$

z=linspace(0,3*pi,200);
xx=zeros(1,length(z));
hold on
plot3(cos(z), xx,z,'r')
plot3(xx, cos(z),z,'b')
z=linspace(0,3*pi,20);
xx=zeros(1,length(z));
quiver3(xx,xx,z,xx,cos(z),xx,0, 'color','b');
quiver3(xx,xx,z,cos(z),xx,xx,0, 'color','r');
hold off
grid on
xlabel('x')
ylabel('y')
zlabel('z')
title('Ondas electromagnéticas')

Vector de Poynting

Se denomina vector de Poynting al producto vectorial

${\displaystyle \overrightarrow{S}=\overrightarrow{E}\times \overrightarrow{H}}$

Cuando se integra sobre una superficie cerrada nos da el flujo total de energía hacia el exterior por unidad de tiempo.

Teniendo en cuenta que el valor medio <cos²(ωt)>=1/2, el valor medio de $\overrightarrow{S}$,

${\displaystyle \langle \overrightarrow{S}\rangle =\frac{1}{2}\sqrt{\frac{\epsilon }{\mu }}{E}_0^2\widehat{k}=v\left(\frac{1}{2}\epsilon E_0^2\right)\widehat{k}}$

Reflexión y refracción de las ondas electromagnéticas

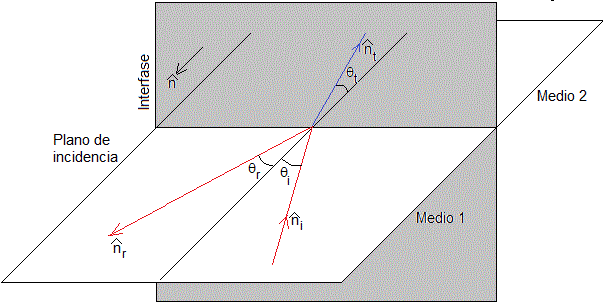
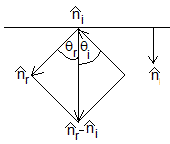
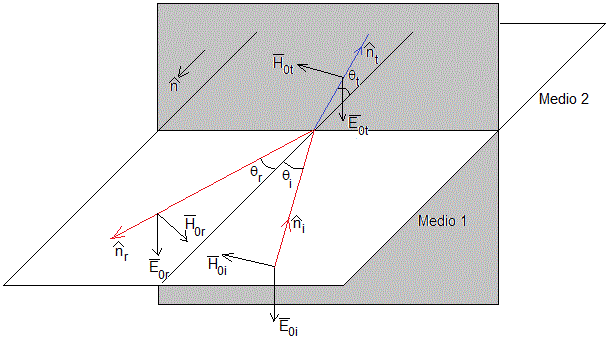
Supongamos dos medios no magnéticos semiinfinitos, lineales, homogéneos e isótropos. Una onda electromagnética que se propaga en el medio 1 incide sobre la superficie de separación de los medios 1 y 2 produciendo una onda reflejada y otra transmitida. Los vectores unitarios ${\widehat{n}}_i$ , ${\widehat{n}}_r$ y ${\widehat{n}}_t$ son normales a los frentes de onda planos (formados por los vectores $\overrightarrow{E}$ y $\overrightarrow{H}$) y tienen el sentido de la propagación $\overrightarrow{E}\times \overrightarrow{H}$

Los ángulos θ_i, θ_r, y θ_t son los ángulos de incidencia, de reflexión y refracción, respectivamente.

Las leyes de la reflexión y la de Snell de la refracción

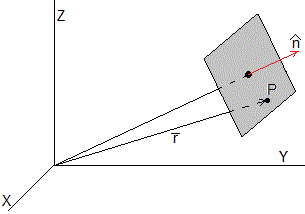
La onda electromagnética incidente está formada por frentes de onda planos perpendiculares al vector ${\widehat{n}}_i$, que señala la dirección de propagación.

Véase en el apartado Vector normal a un plano la ecuación de un plano perpendicular al vector unitario $\widehat{n}$

El campo eléctrico es de la forma

${\displaystyle \overrightarrow{E_i}=\overrightarrow{E_{0i}}\exp \left(i{\omega }_i\left(t-\frac{{\widehat{n}}_i·\overrightarrow{r}}{v_1}\right)\right)}$

v₁ es la velocidad de fase de la onda electromagnética en el medio 1

Tanto la onda relejada como la refractada por la superficie de separación son también planas y polarizadas

${\displaystyle \begin{array}{l}\overrightarrow{E_r}=\overrightarrow{E_{0r}}\exp \left(i{\omega }_r\left(t-\frac{{\widehat{n}}_{r·}\overrightarrow{r}}{v_1}\right)\right)\\ \overrightarrow{E_t}=\overrightarrow{E_{0t}}\exp \left(i{\omega }_t\left(t-\frac{{\widehat{n}}_t·\overrightarrow{r}}{v_2}\right)\right)\end{array}}$

v₂ es la velocidad de fase de la onda electromagnética en el medio 2

Los tres vectores han de ser funciones del tiempo similares, por tanto, las frecuencias han de ser iguales

ω_i=ω_r=ω_t

En cualquier punto de la superficie de separación se deberá cumplir

${\displaystyle \frac{{\widehat{n}}_{i·}\overrightarrow{r}}{v_1}=\frac{{\widehat{n}}_{r·}\overrightarrow{r}}{v_1}=\frac{{\widehat{n}}_{t·}\overrightarrow{r}}{v_2}}$

• La primera ecuación se escribe

${\displaystyle \left({\widehat{n}}_r-{\widehat{n}}_i\right)\overrightarrow{r}=0}$

Como el vector $\overrightarrow{r}$ está en el plano de separación, el vector ${\widehat{n}}_r-{\widehat{n}}_i$ es perpendicular a dicho plano, por tanto los ángulos θ_i=θ_r, el ángulo de reflexión es igual al de incidencia. El plano formado por los dos vectores se denomina de incidencia.

• La segunda ecuación se escribe



${\displaystyle \left(\frac{{\widehat{n}}_i}{v_1}-\frac{{\widehat{n}}_t}{v_2}\right)\overrightarrow{r}=0}$

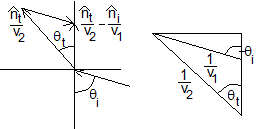
El vector entre paréntesis debe ser normal a la superficie de separación. Se tiene que cumplir que las componentes (véase la figura de la derecha)

${\displaystyle \begin{array}{l}\frac{1}{v_2}\sin {\theta }_t=\frac{1}{v_1}\sin {\theta }_i\\ n_2\sin {\theta }_t=n_1\sin {\theta }_i\end{array}}$

Ecuaciones de Fresnel

Hay dos posibilidades: que el campo eléctrico sea normal al plano de inicidencia y que sea paralelo al mismo

El campo eléctrico es normal al plano de incidencia

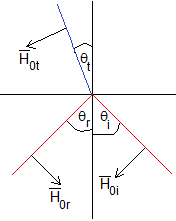
En la superficie de separación, las componentes tangenciales de $\overrightarrow{E}$ Y $\overrightarrow{H}$ son continuas

${\displaystyle \begin{array}{l}{E}_{0i}+E_{0r}=E_{0t}\\ H_{0i}\cos {\theta }_i-H_{0r}\cos {\theta }_r=H_{0t}\cos {\theta }_t\end{array}}$

Teniendo en cuenta la relación entre amplitudes, $H_0=\sqrt{\frac{\epsilon }{\mu }}{E}_0$ y la definición de índice de refracción, $n=\sqrt{{\epsilon }_r{\mu }_r}$, la segunda ecuación se transforma en

${\displaystyle \begin{array}{l}\sqrt{\frac{{\epsilon }_1}{{\mu }_1}}{E}_{0i}\cos {\theta }_i-\sqrt{\frac{{\epsilon }_1}{{\mu }_1}}{E}_{0r}\cos {\theta }_r=\sqrt{\frac{{\epsilon }_2}{{\mu }_2}}{E}_{0t}\cos {\theta }_t\\ \frac{n_1}{{\mu }_{r1}}\left(E_{0i}-E_{0r}\right)\cos {\theta }_i=\frac{n_2}{{\mu }_{r2}}{E}_{0t}\cos {\theta }_t\end{array}}$

Para un medio no magnético, la permeabilidad relativa μ_r≈1. Resolvemos el sistema de dos ecuaciones con dos incógnitas

${\displaystyle \{\begin{array}{l}{E}_{0i}+E_{0r}=E_{0t}\\ n_1\left(E_{0i}-E_{0r}\right)\cos {\theta }_i=n_2{E}_{0t}\cos {\theta }_t\end{array}}$

Despejamos E_0r y E_0t. El resultado es

${\displaystyle {\left(\frac{E_{0t}}{E_{0i}}\right)}_{\perp }=\frac{2\frac{n_1}{n_2}\cos {\theta }_i}{\frac{n_1}{n_2}\cos {\theta }_i+\cos {\theta }_t},{\left(\frac{E_{0r}}{E_{0i}}\right)}_{\perp }=\frac{\frac{n_1}{n_2}\cos {\theta }_i-\cos {\theta }_t}{\frac{n_1}{n_2}\cos {\theta }_i+\cos {\theta }_t}}$

Observamos en las fórmulas que ${\left(\frac{E_{0t}}{E_{0i}}\right)}_{\perp }>0$ , la onda transmitida y la incidente están en fase. Sin embargo, ${\left(\frac{E_{0r}}{E_{0i}}\right)}_{\perp }$ puede ser positivo o negativo.

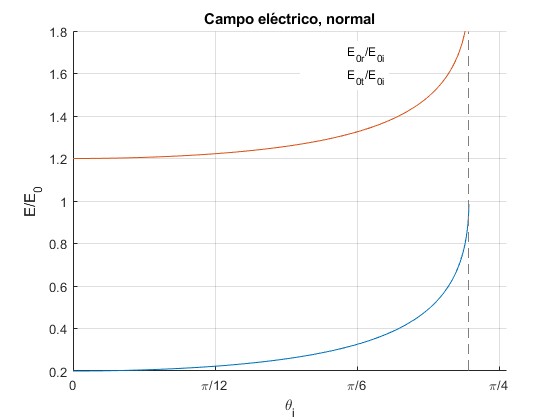
• En fase, n₁>n₂

De la ley de la refracción n₁sinθ_i=n₂sinθ_t, si n₁>n₂, entonces θ_t>θ_i, cosθ_i>cosθ_t, luego ${\left(\frac{E_{0r}}{E_{0i}}\right)}_{\perp }>0$, la onda reflejada está en fase con la incidente.



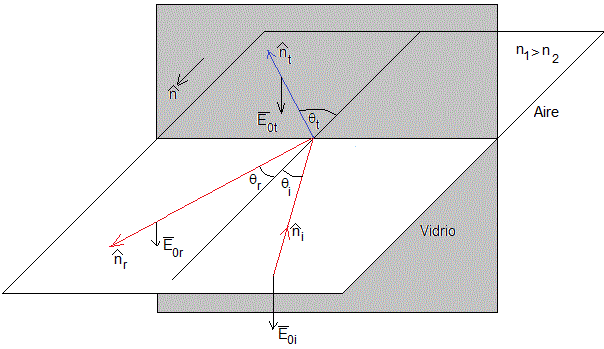
Para el ángulo de incidencia θ_c tal que el ángulo de refracción es θ_t=π/2 (90°), se produce la reflexión total, sinθ_c=n₂/n₁, para θ_i≥θ_c no hay onda refractada

Representamos ${\left(\frac{E_{0t}}{E_{0i}}\right)}_{\perp }$ y ${\left(\frac{E_{0r}}{E_{0i}}\right)}_{\perp }$ para n₁=1.5 y n₂=1

n1=1.5;
n2=1;
th_c=asin(n2/n1); %reflexión total
hold on
r=@(x) ((n1/n2)*cos(x)-cos(asin(n1*sin(x)/n2)))./((n1/n2)*cos(x)
+cos(asin(n1*sin(x)/n2)));
fplot(r,[0,th_c])
t=@(x) 2*(n1/n2)*cos(x)./((n1/n2)*cos(x)+cos(asin(n1*sin(x)/n2)));
fplot(t,[0,th_c])
hold off
grid on
set(gca,'XTick',0:pi/12:pi/2)
set(gca,'XTickLabel',{'0','\pi/12','\pi/6','\pi/4','\pi/3','5\pi/12','\pi/2'})
xlabel('\theta_i')
ylabel('E/E_0')
legend('E_{0r}/E_{0i}', 'E_{0t}/E_{0i}','Location','best')
title('Campo eléctrico, normal')



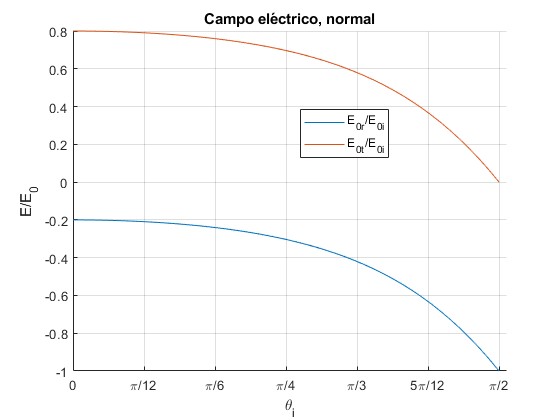
• En oposición de fase, n₁<n₂

De la ley de la refracción n₁sinθ_i=n₂sinθ_t, si n₁<n₂, entonces θ_t<θ_i, cosθ_i<cosθ_t, luego ${\left(\frac{E_{0r}}{E_{0i}}\right)}_{\perp }<0$, la onda reflejada está en oposición de fase (desfasada π) con la incidente.

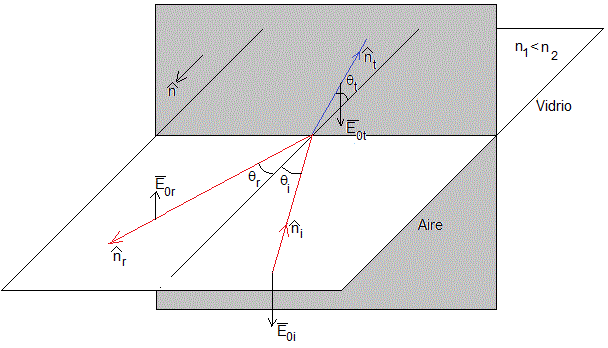
Representamos ${\left(\frac{E_{0t}}{E_{0i}}\right)}_{\perp }$ y ${\left(\frac{E_{0r}}{E_{0i}}\right)}_{\perp }$ para n₁=1 y n₂=1.5

n1=1;
n2=1.5;
hold on
r=@(x) ((n1/n2)*cos(x)-cos(asin(n1*sin(x)/n2)))./((n1/n2)*cos(x)+
cos(asin(n1*sin(x)/n2)));
fplot(r,[0,pi/2])
t=@(x) 2*(n1/n2)*cos(x)./((n1/n2)*cos(x)+cos(asin(n1*sin(x)/n2)));
fplot(t,[0,pi/2])
hold off
grid on
set(gca,'XTick',0:pi/12:pi/2)
set(gca,'XTickLabel',{'0','\pi/12','\pi/6','\pi/4','\pi/3','5\pi/12','\pi/2'})
xlabel('\theta_i')
ylabel('E/E_0')
legend('E_{0r}/E_{0i}', 'E_{0t}/E_{0i}','Location','best')
title('Campo eléctrico, normal')

El campo eléctrico es paralelo al plano de incidencia

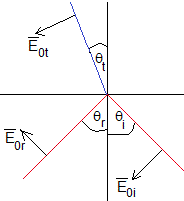
En la superficie de separación, las componentes tangenciales de $\overrightarrow{E}$ Y $\overrightarrow{H}$ son continuas

${\displaystyle \{\begin{array}{l}{H}_{0i}-H_{0r}=H_{0t}\\ E_{0i}\cos {\theta }_i+E_{0r}\cos {\theta }_r=E_{0t}\cos {\theta }_t\end{array}}$

Para un medio no magnético, μ_r≈1. Resolvemos el sistema de dos ecuaciones con dos incógnitas

${\displaystyle \{\begin{array}{l}{n}_1\left(E_{0i}-E_{0r}\right)=n_2{E}_{0t}\\ \left(E_{0i}+E_{0r}\right)\cos {\theta }_i=E_{0t}\cos {\theta }_t\end{array}}$

Despejamos E_0r y E_0t. El resultado es

${\displaystyle {\left(\frac{E_{0t}}{E_{0i}}\right)}_{\parallel }=\frac{2\frac{n_1}{n_2}\cos {\theta }_i}{\cos {\theta }_i+\frac{n_1}{n_2}\cos {\theta }_t},{\left(\frac{E_{0r}}{E_{0i}}\right)}_{\parallel }=\frac{-\cos {\theta }_i+\frac{n_1}{n_2}\cos {\theta }_t}{\cos {\theta }_i+\frac{n_1}{n_2}\cos {\theta }_t}}$

Observamos en las fórmulas que ${\left(\frac{E_{0t}}{E_{0i}}\right)}_{\parallel }>0$ , la onda transmitida y la incidente están en fase. Sin embargo, ${\left(\frac{E_{0r}}{E_{0i}}\right)}_{\parallel }$ puede ser positivo o negativo.

• En fase si, $\frac{n_1}{n_2}\cos {\theta }_t-\cos {\theta }_i>0$

La ley de la refracción, n₁/n₂=sinθ_t/sinθ_i

La desigualdad se transforma en

${\displaystyle \begin{array}{l}\sin {\theta }_t\cos {\theta }_t-\sin {\theta }_i\cos {\theta }_i>0\\ \sin \left(2{\theta }_t\right)-\sin \left(2{\theta }_i\right)>0\end{array}}$

Teniendo en cuenta la relación trigonométrica sin(A+B)-sin(A-B)=2sinB·cosA

${\displaystyle \sin \left({\theta }_t-{\theta }_i\right)\cos \left({\theta }_t+{\theta }_i\right)>0}$

Esta desigualdad se satisface si

${\displaystyle \{\begin{array}{l}{\theta }_t>{\theta }_i,{\theta }_t+{\theta }_i<\frac{\pi }{2}\\ {\theta }_t<{\theta }_i,{\theta }_t+{\theta }_i>\frac{\pi }{2}\end{array}}$

• En oposición de fase si, $\frac{n_1}{n_2}\cos {\theta }_t-\cos {\theta }_i<0$

Si no se cumplen las dos condiciones anteriores

La fase de la onda reflejada depende de n₂/n₁ y también de θ_i y θ_t. La razón ${\left(\frac{E_{0r}}{E_{0i}}\right)}_{\parallel }$, puede ser positiva o negativa tanto para n₂>n₁ como para n₂<n₁

El ángulo de Brewster

El numerador de ${\left(\frac{E_{0r}}{E_{0i}}\right)}_{\parallel }$ se hace cero cuando θ_i+θ_t=π/2.

Cuando el campo eléctrico es paralelo no hay onda reflejada. Para este caso, el ángulo de incidencia θ_i se denomina ángulo de Brewster, θ_B o ángulo polarizante, ya que una onda electromagnética no polarizada se refleja con su vector normal al plano de incidencia

De la ley de la refracción

${\displaystyle \frac{n_1}{n_2}=\frac{\sin {\theta }_t}{\sin {\theta }_B}=\frac{\sin \left(\frac{\pi }{2}-{\theta }_B\right)}{\sin {\theta }_B}=\frac{1}{\tan {\theta }_B}}$

Comparamos el ángulo crítico a partir del cual se produce la reflexión total, sinθ_c=n₂/n₁, con el ángulo de Brewster, tanθ_B=n₂/n₁. Representamos θ_c y θ_B en función de la razón n₁/n₂. La onda electromagnética incide en el medio 1

hold on
fplot(@(x) atan(1./x),[1,10]);
fplot(@(x) asin(1./x),[1,10]);
hold off
grid on
set(gca,'YTick',0:pi/12:pi/2)
set(gca,'YTickLabel',{'0','\pi/12','\pi/6','\pi/4','\pi/3','5\pi/12','\pi/2'})
xlabel('n_1/n_2')
ylabel('\theta_B, \theta_c')
legend('Brewster', 'Reflexión total','Location','best')
title('Angulos crítico y Brewster')

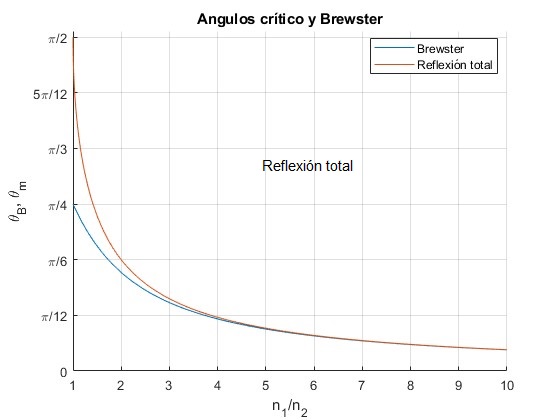
El ángulo crítico θ_m, es mayor que el ángulo de Brewster, θ_B

Representamos ${\left(\frac{E_{0t}}{E_{0i}}\right)}_{\parallel }$ y ${\left(\frac{E_{0r}}{E_{0i}}\right)}_{\parallel }$ para n₁=1 y n₂=1.5. Se señala mediante una línea vertical a trazos el ángulo de Brewster

n1=1;
n2=1.5;
hold on
r=@(x) ((n1/n2)*cos(asin(n1*sin(x)/n2))-cos(x))./((n1/n2)*cos(asin(n1*sin(x)/n2))
+cos(x));
fplot(r,[0,pi/2])
t=@(x) 2*(n1/n2)*cos(x)./((n1/n2)*cos(asin(n1*sin(x)/n2))+cos(x));
fplot(t,[0,pi/2])
ang_B=atan(n2/n1); %ángulo de Brewster
line([ang_B, ang_B],[0,1],'lineStyle','--')
hold off
grid on
set(gca,'XTick',0:pi/12:pi/2)
set(gca,'XTickLabel',{'0','\pi/12','\pi/6','\pi/4','\pi/3','5\pi/12','\pi/2'})
xlabel('\theta_i')
ylabel('E/E_0')
legend('E_{0r}/E_{0i}', 'E_{0t}/E_{0i}','Location','best')
title('Campo eléctrico, paralelo')

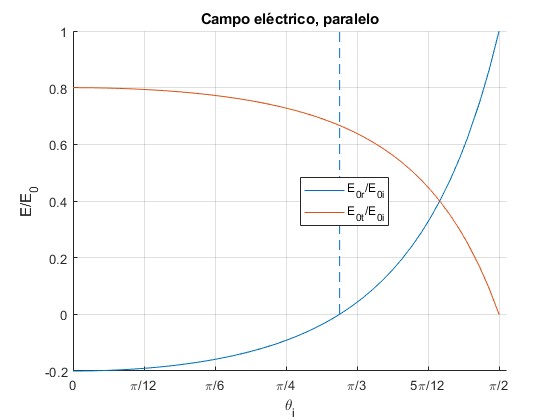
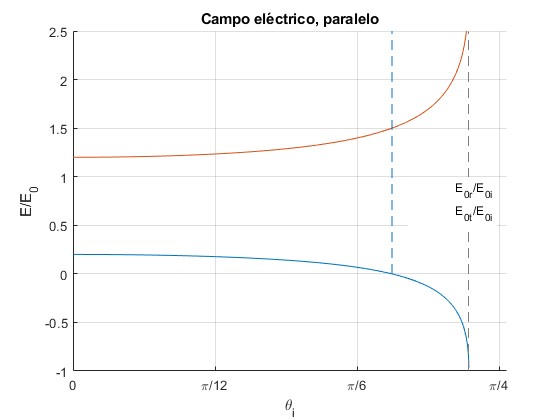
Representamos ${\left(\frac{E_{0t}}{E_{0i}}\right)}_{\parallel }$ y ${\left(\frac{E_{0r}}{E_{0i}}\right)}_{\parallel }$ para n₁=1.5 y n₂=1. Se señala mediante una línea vertical a trazos el ángulo de Brewster

n1=1.5;
n2=1;
th_c=asin(n2/n1); %reflexión total
hold on
r=@(x) ((n1/n2)*cos(asin(n1*sin(x)/n2))-cos(x))./((n1/n2)*
cos(asin(n1*sin(x)/n2))+cos(x));
fplot(r,[0,th_c])
t=@(x) 2*(n1/n2)*cos(x)./((n1/n2)*cos(asin(n1*sin(x)/n2))+cos(x));
fplot(t,[0,th_c])
ang_B=atan(n2/n1); %ángulo de Brewster
line([ang_B, ang_B],[0,2.5],'lineStyle','--')
hold off
grid on
set(gca,'XTick',0:pi/12:pi/2)
set(gca,'XTickLabel',{'0','\pi/12','\pi/6','\pi/4','\pi/3','5\pi/12','\pi/2'})
xlabel('\theta_i')
ylabel('E/E_0')
legend('E_{0r}/E_{0i}', 'E_{0t}/E_{0i}','Location','best')
title('Campo eléctrico, paralelo')

Coeficientes de reflexión y transmisión

El flujo medio de energía por unidad de área en la onda incidente está dada por el valor medio del vector de Poynting. Para un medio no conductor y no magnético μ_r≈1

${\displaystyle \begin{array}{l}\langle \overrightarrow{S_i}\rangle =\frac{1}{2}\sqrt{\frac{{\epsilon }_1}{{\mu }_0{\mu }_{r1}}}{E}_{0i}^2{\widehat{n}}_i=\frac{1}{2}\sqrt{\frac{{\epsilon }_1}{{\mu }_0}}{E}_{0i}^2{\widehat{n}}_i\\ \langle \overrightarrow{S_r}\rangle =\frac{1}{2}\sqrt{\frac{{\epsilon }_1}{{\mu }_0}}{E}_{0r}^2{\widehat{n}}_r\\ \langle \overrightarrow{S_t}\rangle =\frac{1}{2}\sqrt{\frac{{\epsilon }_2}{{\mu }_0}}{E}_{0t}^2{\widehat{n}}_t\end{array}}$

Los coeficientes de reflexión R y transmisión T se definen como los flujos por unidad de tiempo y área en la separación, $\widehat{n}$ es el vector unitario normal a la superficie de separación.

${\displaystyle \begin{array}{l}R=\left|\frac{\langle \overrightarrow{S_r}\rangle ·\widehat{n}}{\langle \overrightarrow{S_i}\rangle ·\widehat{n}}\right|=\left|\frac{\widehat{n}·{\widehat{n}}_r}{\widehat{n}·{\widehat{n}}_i}\right|\frac{E_{0r}^2}{E_{0i}^2}=\frac{\cos {\theta }_i}{\cos {\theta }_i}\frac{E_{0r}^2}{E_{0i}^2}=\frac{E_{0r}^2}{E_{0i}^2}\\ T=\left|\frac{\langle \overrightarrow{S_t}\rangle ·\widehat{n}}{\langle \overrightarrow{S_i}\rangle ·\widehat{n}}\right|=\sqrt{\frac{{\epsilon }_{rt}}{{\epsilon }_{ri}}}\frac{E_{0r}^2}{E_{0i}^2}\left|\frac{\widehat{n}·{\widehat{n}}_t}{\widehat{n}·{\widehat{n}}_i}\right|=\frac{n_2}{n_1}\frac{E_{0r}^2\cos {\theta }_t}{E_{0i}^2\cos {\theta }_i}\end{array}}$

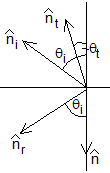
• El campo eléctrico es perpendicular al plano de inicidencia

${\displaystyle \begin{array}{l}{T}_{\perp }={\left(\frac{2\frac{n_1}{n_2}\cos {\theta }_i}{\frac{n_1}{n_2}\cos {\theta }_i+\cos {\theta }_t}\right)}^2\frac{n_2\cos {\theta }_t}{n_1\cos {\theta }_i}=\frac{4\frac{n_1}{n_2}\cos {\theta }_i\cos {\theta }_t}{{\left(\frac{n_1}{n_2}\cos {\theta }_i+\cos {\theta }_t\right)}^2}\\ R_{\perp }={\left(\frac{\frac{n_1}{n_2}\cos {\theta }_i-\cos {\theta }_t}{\frac{n_1}{n_2}\cos {\theta }_i+\cos {\theta }_t}\right)}^2\end{array}}$

Comprobamos que R+T=1

Representamos los coeficientes R y T para n₁=1 y n₂=1.5

n1=1;
n2=1.5;
hold on
R=@(x) (((n1/n2)*cos(x)-cos(asin(n1*sin(x)/n2)))./((n1/n2)*cos(x)+
cos(asin(n1*sin(x)/n2)))).^2;
fplot(R,[0,pi/2])
T=@(x) 4*(n1/n2)*(cos(x).*cos(asin(n1*sin(x)/n2)))./((n1/n2)*cos(x)+
cos(asin(n1*sin(x)/n2))).^2;
fplot(T,[0,pi/2])
hold off
grid on
set(gca,'XTick',0:pi/12:pi/2)
set(gca,'XTickLabel',{'0','\pi/12','\pi/6','\pi/4','\pi/3','5\pi/12','\pi/2'})
xlabel('\theta_i')
ylabel('R,T')
legend('R', 'T','Location','best')
title('Campo eléctrico, normal')



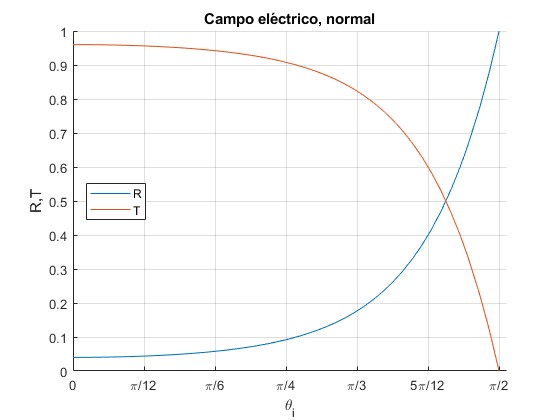
Representamos los coeficientes R y T para n₁=1.5 y n₂=1

n1=1.5;
n2=1;
th_c=asin(n2/n1); %reflexión total
hold on
R=@(x) (((n1/n2)*cos(x)-cos(asin(n1*sin(x)/n2)))./((n1/n2)*cos(x)+
cos(asin(n1*sin(x)/n2)))).^2;
fplot(R,[0,th_c])
T=@(x) 4*(n1/n2)*(cos(x).*cos(asin(n1*sin(x)/n2)))./((n1/n2)*cos(x)+
cos(asin(n1*sin(x)/n2))).^2;
fplot(T,[0,th_c])
hold off
grid on
set(gca,'XTick',0:pi/12:pi/2)
set(gca,'XTickLabel',{'0','\pi/12','\pi/6','\pi/4','\pi/3','5\pi/12','\pi/2'})
xlabel('\theta_i')
ylabel('R,T')
legend('R', 'T','Location','best')
title('Campo eléctrico, normal')



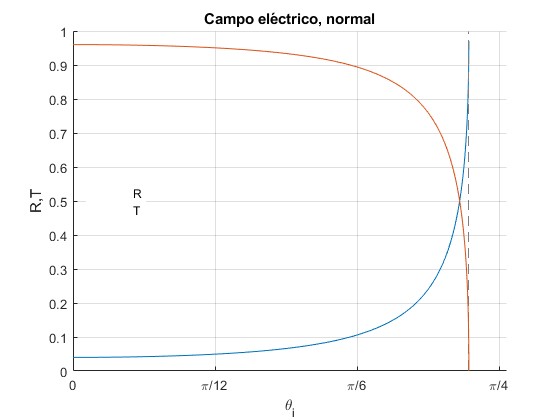
• El campo eléctrico es paralelo al plano de inicidencia

${\displaystyle \begin{array}{l}{T}_{\parallel }={\left(\frac{2\frac{n_1}{n_2}\cos {\theta }_i}{\cos {\theta }_i+\frac{n_1}{n_2}\cos {\theta }_t}\right)}^2\frac{n_2\cos {\theta }_t}{n_1\cos {\theta }_i}=\frac{4\frac{n_1}{n_2}\cos {\theta }_i\cos {\theta }_t}{{\left(\cos {\theta }_i+\frac{n_1}{n_2}\cos {\theta }_t\right)}^2}\\ R_{\parallel }={\left(\frac{-\cos {\theta }_i+\frac{n_1}{n_2}\cos {\theta }_t}{\cos {\theta }_i+\frac{n_1}{n_2}\cos {\theta }_t}\right)}^2\end{array}}$

Comprobamos que R+T=1

Angulo de Brewster

${\displaystyle \begin{array}{l}\frac{n_1}{n_2}=\frac{\cos {\theta }_{iB}}{\sin {\theta }_{iB}}\\ {\theta }_{iB}+{\theta }_{tB}=\frac{\pi }{2},\cos {\theta }_{tB}=\sin {\theta }_{iB},\cos {\theta }_{iB}=\sin {\theta }_{tB}\end{array}}$

Teniendo en cuenta estas relaciones, comprobamos que

${\displaystyle T_{\parallel }=\mathrm{1,}{R}_{\parallel }=0}$

Representamos los coeficientes R y T para n₁=1 y n₂=1.5. Se señala mediante una línea vertical el ángulo de Brewster

n1=1;
n2=1.5;
hold on
R=@(x) (((n1/n2)*cos(asin(n1*sin(x)/n2))-cos(x))./((n1/n2)*
cos(asin(n1*sin(x)/n2))+cos(x))).^2;
fplot(R,[0,pi/2])
T=@(x) 4*(n1/n2)*(cos(x).*cos(asin(n1*sin(x)/n2)))./((n1/n2)*
cos(asin(n1*sin(x)/n2))+cos(x)).^2;
fplot(T,[0,pi/2])
ang_B=atan(n2/n1); %ángulo de Brewster
line([ang_B, ang_B],[0,1],'lineStyle','--')
hold off
grid on
set(gca,'XTick',0:pi/12:pi/2)
set(gca,'XTickLabel',{'0','\pi/12','\pi/6','\pi/4','\pi/3','5\pi/12','\pi/2'})
xlabel('\theta_i')
ylabel('R,T')
legend('R', 'T','Location','best')
title('Campo eléctrico, paralelo')



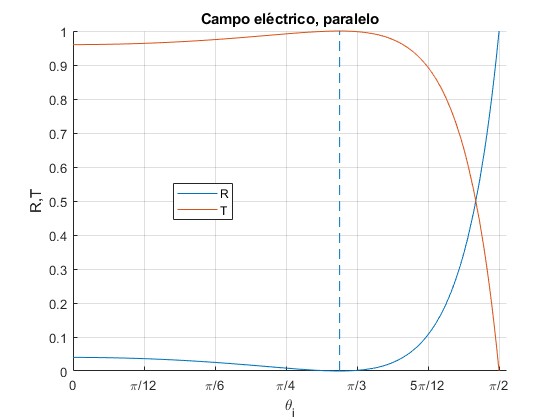
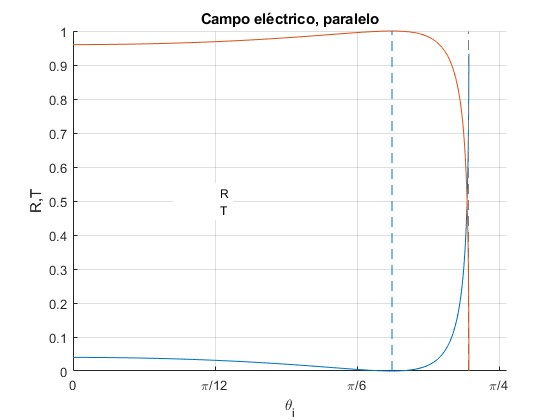
Representamos los coeficientes R y T para n₁=1.5 y n₂=1. Se señala mediante una línea vertical el ángulo de Brewster

n1=1.5;
n2=1;
th_c=asin(n2/n1); %reflexión total
hold on
R=@(x) (((n1/n2)*cos(asin(n1*sin(x)/n2))-cos(x))./((n1/n2)*
cos(asin(n1*sin(x)/n2))+cos(x))).^2;
fplot(R,[0,th_c])
T=@(x) 4*(n1/n2)*(cos(x).*cos(asin(n1*sin(x)/n2)))./((n1/n2)*
cos(asin(n1*sin(x)/n2))+cos(x)).^2;
fplot(T,[0,th_c])
ang_B=atan(n2/n1); %ángulo de Brewster
line([ang_B, ang_B],[0,1],'lineStyle','--')
hold off
grid on
set(gca,'XTick',0:pi/12:pi/2)
set(gca,'XTickLabel',{'0','\pi/12','\pi/6','\pi/4','\pi/3','5\pi/12','\pi/2'})
xlabel('\theta_i')
ylabel('R,T')
legend('R', 'T','Location','best')
title('Campo eléctrico, paralelo')

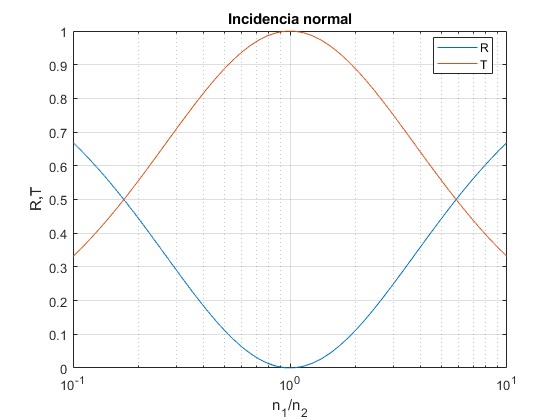
Incidencia normal

Para la incidencia normal θ_i=θ_t=0, el plano de incidencia está indeterminado y las dos pares de fórmulas (paralelo y perpendicular) coinciden.

Representamos los coeficientes R y T para valores de n₁/n₂ comprendidos entre 0.1 y 10

x=logspace(-1,1);
R=@(x) ((x-1)./(x+1)).^2;
T=@(x) 4*x./(x+1).^2;
semilogx(x,R(x),x, T(x))
grid on
xlabel('n_1/n_2')
ylabel('R,T')
legend('R', 'T','Location','best')
title('Incidencia normal')

Onda incidente, reflejada y transmitida

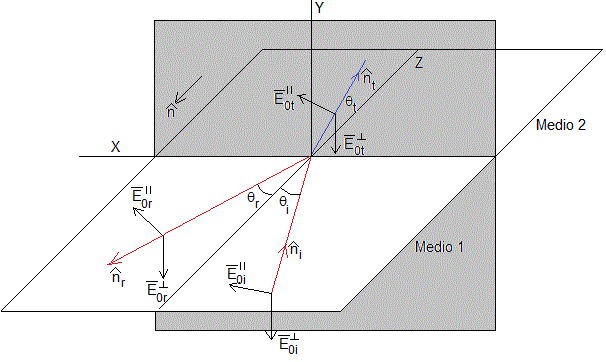
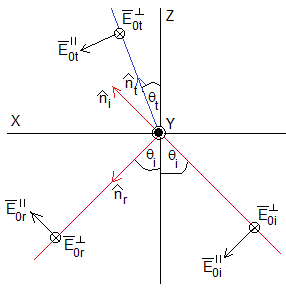
Hay muchas maneras de disponer los ejes. El plano de incidencia es el plano XZ y la perpendicular a este plano es el eje Y. Los vectores unitarios, se expresan en este Sistema de Referencia

${\displaystyle \begin{array}{l}{\widehat{n}}_i=\sin {\theta }_i\widehat{i}+\cos {\theta }_i\widehat{k}\\ {\widehat{n}}_r=\sin {\theta }_i\widehat{i}-\cos {\theta }_i\widehat{k}\\ {\widehat{n}}_t=\sin {\theta }_t\widehat{i}+\cos {\theta }_t\widehat{k}\end{array}}$

A continuación, damos las expresiones del campo eléctrico incidente, reflejado y transmitido

Las ecuaciones de Fresnel establecen las relaciones entre las amplitudes de la onda reflejada E_0r y la incidente, E_0i; entre las amplitudes de la onda transmitida E_0t y la incidente, cuando

• El campo eléctrico es normal ⊥ al plano de incidencia
• El campo eléctrico es paralelo ∥ al plano de incidencia

${\displaystyle \begin{array}{l}{\overrightarrow{E}}_i=\left(E_{0i}^{\parallel }\cos {\theta }_i\widehat{i}-E_{0i}^{\parallel }\sin {\theta }_i\widehat{k}-E_{0i}^{\perp }\widehat{j}\right)\exp \left(i\omega \left(t-\frac{x\sin {\theta }_i+z\cos {\theta }_i}{v_1}\right)\right)\\ {\overrightarrow{E}}_r=\left(E_{0r}^{\parallel }\cos {\theta }_i\widehat{i}+E_{0r}^{\parallel }\sin {\theta }_i\widehat{k}-E_{0r}^{\perp }\widehat{j}\right)\exp \left(i\omega \left(t-\frac{x\sin {\theta }_i-z\cos {\theta }_i}{v_1}\right)\right)\\ {\overrightarrow{E}}_t=\left(E_{0t}^{\parallel }\cos {\theta }_t\widehat{i}-E_{0t}^{\parallel }\sin {\theta }_t\widehat{k}-E_{0t}^{\perp }\widehat{j}\right)\exp \left(i\omega \left(t-\frac{x\sin {\theta }_t+z\cos {\theta }_t}{v_2}\right)\right)\end{array}}$

Reflexión total

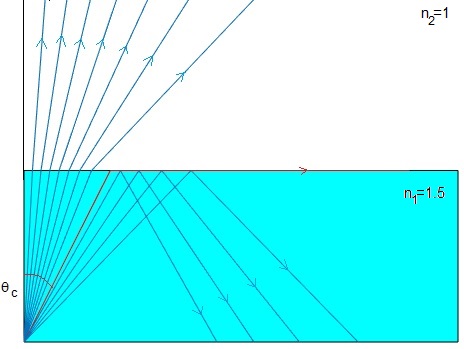
n1=1.5;
n2=1;
fill([0, 4.5,4.5,0],[0,0,-1,-1],'c')
th_c=asin(n2/n1);
for th=(5:5:35)*pi/180
    line([0,tan(th)],[-1,0])
    th_t=asin(n1*sin(th)/n2);
    line([tan(th),tan(th)+tan(th_t)],[0,1])
end
line([0,tan(th_c)],[-1,0],'color','r')
line([tan(th_c), 4],[0,0],'color','r')
for th=(45:5:60)*pi/180
    line([0,tan(th)],[-1,0])
    line([tan(th),2*tan(th)],[0,-1])
end
axis off

Cuando el índice de refracción del medio 1 es mayor que el índice de refracción del medio 2, n₁>n₂, de acuerdo con la ley de la refracción, n₁sinθ_i=n₂sinθ_t, el ángulo θ_t>θ_i. Se denomina ángulo crítico θ_c al ángulo de la ónda incidente que corresponde a θ_t=π/2. Si el ángulo de la onda incidente es mayor o igual al crítico θ_i≥θ_c, solamente hay onda reflejada, no hay onda transmitida al segundo medio

${\displaystyle \begin{array}{l}{n}_1\sin {\theta }_c=n_2,\sin {\theta }_c=\frac{n_2}{n_1}\\ {\theta }_i>{\theta }_c,n_1\sin {\theta }_i=n_2\sin {\theta }_t,\sin {\theta }_t>1\\ \cos {\theta }_t=\pm \sqrt{1-{\sin }^2{\theta }_t}=\pm \sqrt{1-{\left(\frac{n_1}{n_2}\right)}^2{\sin }^2{\theta }_i}=\pm i\frac{n_1}{n_2}\sqrt{{\sin }^2{\theta }_i-{\left(\frac{n_2}{n_1}\right)}^2}\end{array}}$

Para θ_i>θ_c, cosθ_t es un número imaginario y solamente tiene sentido, el signo - delante de la unidad imaginaria

El campo eléctrico es perpendicular al plano de incidencia

Analizamos el caso más simple, el campo eléctrico es perpendicular al plano de incidencia

${\displaystyle \begin{array}{l}{\overrightarrow{E}}_t^{\perp }=-E_{0t}\widehat{j}\exp \left(i\omega \left(t-\frac{x\sin {\theta }_t+z\cos {\theta }_t}{v_2}\right)\right)\\ {\overrightarrow{E}}_t^{\perp }=-E_{0t}\widehat{j}\exp \left(i\omega \left(t-\frac{x\frac{n_1}{n_2}\sin {\theta }_i-iz\frac{n_1}{n_2}\sqrt{{\sin }^2{\theta }_i-{\left(\frac{n_2}{n_1}\right)}^2}}{\frac{c}{n_2}}\right)\right)\\ {\overrightarrow{E}}_t^{\perp }=-E_{0t}\widehat{j}\exp \left(-z\frac{\omega }{v_1}\sqrt{{\sin }^2{\theta }_i-{\left(\frac{n_2}{n_1}\right)}^2}\right)\exp \left(i\omega \left(t-\frac{x\sin {\theta }_i}{v_1}\right)\right)\end{array}}$

La onda transmitida se propaga a lo largo del eje X en la superficie de separación

${\displaystyle \begin{array}{l}\frac{2\pi }{{\lambda }_x}=\omega \frac{\sin {\theta }_i}{v_1}\\ \frac{2\pi }{{\lambda }_x}=\frac{\omega }{c}{n}_1\sin {\theta }_i\\ {\lambda }_x=\frac{{\lambda }_0}{n_1\sin {\theta }_i}=\frac{{\lambda }_1}{\sin {\theta }_i}\end{array}}$

siendo λ₁ la longitud de onda en el medio 1

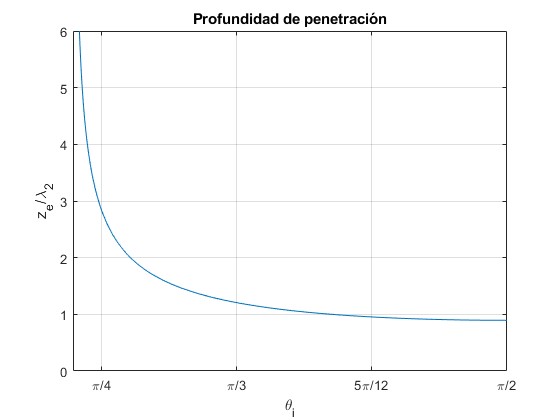
Se amortigua exponencialmente en el segundo medio, la amplitud se reduce en un factor 1/e a una distancia z_e que se denomina profundidad de penetración

${\displaystyle \begin{array}{l}{z}_e\frac{\omega }{v_1}\sqrt{{\sin }^2{\theta }_i-{\left(\frac{n_2}{n_1}\right)}^2}=1\\ z_e\frac{\omega }{v_2}\sqrt{{\left(\frac{n_1}{n_2}\right)}^2{\sin }^2{\theta }_i-1}=1\\ z_e\frac{2\pi }{{\lambda }_2}\sqrt{{\left(\frac{n_1}{n_2}\right)}^2{\sin }^2{\theta }_i-1}=1\\ z_e=\left(\frac{{\lambda }_2}{2\pi }\right)\frac{1}{\sqrt{{\left(\frac{n_1}{n_2}\right)}^2{\sin }^2{\theta }_i-1}}\end{array}}$

donde λ₂=2π·v₂/ω es la longitud de onda en el medio 2

Representamos 2π·z_e/λ₂ en función del ángulo de incidencia θ_i para n₁=1.5 y n₂=1

n1=1.5;
n2=1;
th_c=asin(n2/n1); %ángulo crítico
fplot(@(x) 1./sqrt((n1*sin(x)/n2).^2-1),[th_c,pi/2]);
grid on
set(gca,'XTick',0:pi/12:pi/2)
set(gca,'XTickLabel',{'0','\pi/12','\pi/6','\pi/4','\pi/3','5\pi/12','\pi/2'})
xlabel('\theta_i')
ylim([0,6])
ylabel('z_e/\lambda_2')
title('Profundidad de penetración')

Diferencia de fase entre la onda incidente y reflejada

Las ecuaciones de Fresnel cuando el campo eléctrico es perpendicular al plano de incidencia son ahora cocientes de números complejos

${\displaystyle {\left(\frac{E_{0t}}{E_{0i}}\right)}_{\perp }=\frac{2\frac{n_1}{n_2}\cos {\theta }_i}{\frac{n_1}{n_2}\cos {\theta }_i-i\frac{n_1}{n_2}\sqrt{{\sin }^2{\theta }_i-{\left(\frac{n_2}{n_1}\right)}^2}},{\left(\frac{E_{0r}}{E_{0i}}\right)}_{\perp }=\frac{\frac{n_1}{n_2}\cos {\theta }_i+i\frac{n_1}{n_2}\sqrt{{\sin }^2{\theta }_i-{\left(\frac{n_2}{n_1}\right)}^2}}{\frac{n_1}{n_2}\cos {\theta }_i-i\frac{n_1}{n_2}\sqrt{{\sin }^2{\theta }_i-{\left(\frac{n_2}{n_1}\right)}^2}}}$

Recordando la forma polar de un número complejo

${\displaystyle a+ib=\sqrt{a^2+b^2}\exp \left(i\arctan \frac{b}{a}\right)}$

• Onda reflejada

La primera ecuación de Fresnel se expresan

${\displaystyle \begin{array}{l}\frac{a+ib}{a-ib}=\exp \left(2i\arctan \frac{b}{a}\right)\\ {\left(\frac{E_{0r}}{E_{0i}}\right)}_{\perp }=\frac{\cos {\theta }_i+i\sqrt{{\sin }^2{\theta }_i-{\left(\frac{n_2}{n_1}\right)}^2}}{\cos {\theta }_i-i\sqrt{{\sin }^2{\theta }_i-{\left(\frac{n_2}{n_1}\right)}^2}}=\exp \left(i\alpha \right),\alpha =2\arctan \frac{\sqrt{{\sin }^2{\theta }_i-{\left(\frac{n_2}{n_1}\right)}^2}}{\cos {\theta }_i}\end{array}}$

La amplitud de la onda reflejada es igual a la de la onda incidente, el coeficiente de reflexión es la unidad

${\displaystyle R_{\perp }=\left(\frac{a+bi}{a-bi}\right)\left(\frac{a-bi}{a+bi}\right)=\mathrm{1,}\{\begin{array}{l}a=\cos {\theta }_i\\ b=\sqrt{{\sin }^2{\theta }_i-{\left(\frac{n_2}{n_1}\right)}^2}\end{array}}$

La energía se refleja totalmente y no existe flujo neto de energía a través de la separación

Representamos el ángulo α en función del ángulo de incidencia, θ_i≥θ_c para n₁=1.5 y n₂=1

n1=1.5;
n2=1;
th_c=asin(n2/n1);
fplot(@(x) 2*atan(sqrt(sin(x).^2-(n2/n1)^2)./cos(x)),[th_c,pi/2]);
grid on
set(gca,'XTick',0:pi/12:pi/2)
set(gca,'XTickLabel',{'0','\pi/12','\pi/6','\pi/4','\pi/3','5\pi/12','\pi/2'})
set(gca,'YTick',0:pi/6:pi)
set(gca,'YTickLabel',{'0','\pi/6','\pi/3','\pi/2','2\pi/3','5\pi/6','\pi'})
xlabel('\theta_i')
ylabel('\alpha')
title('Reflexión total')



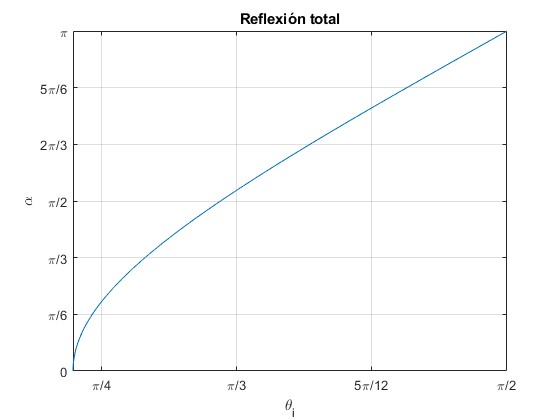
El cambio de fase α en la reflexión varía de cero para el ángulo crítico θ_c a π (180°) para θ_i=π/2

• Onda transmitida

Para la onda transmitida es evidente que E_0t no es cero a pesar de que es nulo el flujo neto de energía a través de la superficie de separación.

${\displaystyle \begin{array}{l}\frac{2a}{a-ib}=\frac{2a}{\sqrt{a^2+b^2}\exp \left(-i\arctan \frac{b}{a}\right)}\\ {\left(\frac{E_{0t}}{E_{0i}}\right)}_{\perp }=\frac{2\cos {\theta }_i}{\cos {\theta }_i-i\sqrt{{\sin }^2{\theta }_i-{\left(\frac{n_2}{n_1}\right)}^2}}=\frac{2\cos {\theta }_i}{\sqrt{1-{\left(\frac{n_2}{n_1}\right)}^2}}\exp \left(i\frac{\alpha }{2}\right)\end{array}}$

Referencias

Paul Lorrain, Dale R. Corson. Campos y ondas electromagnéticas. Selecciones Científicas. 1972