La ecuación de onda es una ecuación diferencial en derivadas parciales, lineal, de segundo orden que describe la propagación de una variedad de ondas

${\displaystyle \frac{{\partial }^2\psi }{\partial t^2}=c^2\frac{{\partial }^2\psi }{\partial x^2},-\infty <x<\infty ,t>0}$

Supongamos una cuerda de longitud infinita, con unas características tales que las ondas se propagan en este medio con velocidad c. Vamos a obtener la solución de esta ecuación diferencial en derivadas parciales para las condiciones iniciales

${\displaystyle \begin{array}{l}\psi (x\mathrm{,0})=F(x)\\ {\frac{\partial \psi (x,t)}{\partial t}|}_{t=0}=G(x)\end{array}}$

F(x) describe la forma inicial t=0, de la cuerda y G(x), la velocidad inicial de los puntos de la cuerda

Solución d'Alembert

Escribimos el operador

${\displaystyle \frac{{\partial }^2}{\partial t^2}-c^2\frac{{\partial }^2}{\partial x^2}=\left(\frac{\partial }{\partial t}+c\frac{\partial }{\partial x}\right)\left(\frac{\partial }{\partial t}-c\frac{\partial }{\partial x}\right)}$

Sustituimos las variables x y t, por ξ=x-ct y η=x-ct

${\displaystyle \begin{array}{l}\frac{\partial }{\partial t}=\frac{\partial \xi }{\partial t}\frac{\partial }{\partial \xi }+\frac{\partial \eta }{\partial t}\frac{\partial }{\partial \eta }=-c\frac{\partial }{\partial \xi }+c\frac{\partial }{\partial \eta }\\ \frac{\partial }{\partial x}=\frac{\partial \xi }{\partial x}\frac{\partial }{\partial \xi }+\frac{\partial \eta }{\partial x}\frac{\partial }{\partial \eta }=\frac{\partial }{\partial \xi }+\frac{\partial }{\partial \eta }\end{array}}$

Utilizando estos resultados la ecuación de onda se reduce a

${\displaystyle \begin{array}{l}\left(\frac{\partial }{\partial t}-c\frac{\partial }{\partial x}\right)\left(\frac{\partial }{\partial t}+c\frac{\partial }{\partial x}\right)\psi =\left(-c\frac{\partial }{\partial \xi }+c\frac{\partial }{\partial \eta }+c\frac{\partial }{\partial \xi }+c\frac{\partial }{\partial \eta }\right)\left(-c\frac{\partial }{\partial \xi }+c\frac{\partial }{\partial \eta }-c\frac{\partial }{\partial \xi }-c\frac{\partial }{\partial \eta }\right)\psi \\ =\left(2c\frac{\partial }{\partial \eta }\right)\left(-2c\frac{\partial }{\partial \xi }\right)\psi =0\end{array}}$

una expresión muy simple

${\displaystyle \frac{\partial }{\partial \eta }\frac{\partial \psi }{\partial \xi }=0}$

Integramos esta ecuación diferencial

${\displaystyle \begin{array}{l}\frac{\partial \psi }{\partial \xi }=f(\xi )\\ \psi (\xi ,\eta )={\displaystyle \int f(\xi )d\xi +v(\eta )}=u(\xi )+v(\eta )\end{array}}$

Volviendo a las variables originales x y t

${\displaystyle \psi (x,t)=u(x-ct)+v(x+ct)}$

No es una tarea fácil encontrar las funciones u y v que satisfacen las condiciones iniciales.

• u(x-ct) representa una perturbación cuya forma es u(x) que se propaga sin distorsión a lo largo del eje X hacia la derecha con velocidad c.

• v(x+ct) representa una perturbación cuya forma es v(x) que se propaga sin distorsión a lo largo del eje X hacia la izquierda con velocidad c.

La solución de la ecuación diferencial en derivadas parciales es la suma de dos ondas que se propagan a lo largo del eje X en sentidos contrarios. El siguiente paso es determinar la forma de las funciones u y v dadas las condiciones iniciales

• La primera condición inicial se refiere al desplazamiento inicial de los puntos de la cuerda

${\displaystyle \begin{array}{l}\psi (x\mathrm{,0})=F(x)\\ F(x)=u(x)+v(x)\end{array}}$

• La segunda condición inicial se refiere a la velocidad inicial de los puntos de la cuerda

${\displaystyle \frac{\partial \psi (\xi ,\eta )}{\partial t}=\frac{\partial \xi }{\partial t}\frac{\partial \psi }{\partial \xi }+\frac{\partial \eta }{\partial t}\frac{\partial \psi }{\partial \eta }=-c\frac{\partial \psi }{\partial \xi }+c\frac{\partial \psi }{\partial \eta }=-c\frac{du}{d\xi }+c\frac{dv}{d\eta }}$

Volviendo a las variables originales x y t

${\displaystyle \begin{array}{l}{\frac{\partial \psi (x,t)}{\partial t}|}_{t=0}=-c\frac{du}{dx}+c\frac{dv}{dx}=G(x)\\ v(x)-u(x)=\frac{1}{c}{\displaystyle \underset{x_0}{\overset{x}{\int }}G(s)ds}\end{array}}$

La constante de integración se ha incorporado en el límite inferior x₀

Tenemos un sistema de dos ecuaciones con dos incógnitas u(x) y v(x)

${\displaystyle \begin{array}{l}v(x)=\frac{1}{2}F(x)+\frac{1}{2c}{\displaystyle \underset{x_0}{\overset{x}{\int }}G(s)ds}\\ u(x)=\frac{1}{2}F(x)-\frac{1}{2c}{\displaystyle \underset{x_0}{\overset{x}{\int }}G(s)ds}\end{array}}$

La solución de la ecuación de ondas es

${\displaystyle \begin{array}{l}\psi (x,t)=u(x-ct)+v(x+ct)=\\ \frac{1}{2}F(x-ct)-\frac{1}{2c}{\displaystyle \underset{x_0}{\overset{x-ct}{\int }}G(s)ds}+\frac{1}{2}F(x+ct)+\frac{1}{2c}{\displaystyle \underset{x_0}{\overset{x+ct}{\int }}G(s)ds}=\\ \psi (x,t)=\frac{F(x-ct)+F(x+ct)}{2}+\frac{1}{2c}{\displaystyle \underset{x-ct}{\overset{x+ct}{\int }}G(s)ds}\end{array}}$

La solución de la ecuación de ondas en el punto x_p y en un instante t_p es

${\displaystyle \psi (x_p,t_p)=\frac{F(x_p-c{t}_p)+F(x_p+c{t}_p)}{2}+\frac{1}{2c}{\displaystyle \underset{x_p-c{t}_p}{\overset{x_p+c{t}_p}{\int }}G(s)ds}}$

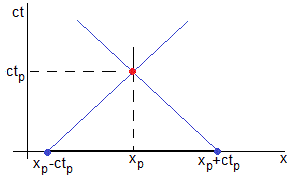
depende de los valores de la función F(x) en los extremos del intervalo [x_p-ct_p, x_p+ct_p] y de los valores de G(x) en todos los puntos de dicho intervalo. Este intervalo se llama domino de dependencia. Esto es debido a que los efectos de la perturbación inicial se propagan con velocidad finita c, por lo que solamente una parte de los datos iniciales afectan la solución de la ecuación de ondas en el punto x_p y en el instante t_p. Los datos iniciales fuera de dicho intervalo no tienen influencia

Cuerda infinita

Vamos a ilustrar la solución de d'Alembert, mediante algunos ejemplos y animaciones para una cuerda de longitud infinita

Solución con velocidad inicial nula, G(x)=0

Consideremos una cuerda infinita, con una forma inicial dada por la función F(x) y con velocidad inicial nula, G(x)=0. La solución de la ecuación de onda es el promedio de dos perturbaciones que se propagan sin distorsión a lo largo del eje X en sentidos opuestos

${\displaystyle \psi (x,t)=\frac{F(x-ct)+F(x+ct)}{2}}$

Ejemplo 1

Sea F(x)=A·exp(-x²)sinx

${\displaystyle \psi (x,t)=\frac{A}{2}\left\{\exp \left(-{\left(x-ct\right)}^2\right)\sin \left(x-ct\right)+\exp \left(-{\left(x+ct\right)}^2\right)\sin \left(x+ct\right)\right\}}$

En color azul, se muestra F(x+ct), que se propaga hacia la izquierda y en color rojo F(x-ct) que se propaga hacia la derecha. En color negro, el promedio, ψ(x,t)

Ejemplo 2

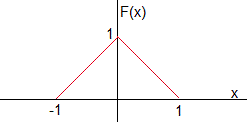
Sea

${\displaystyle F(x)=\{\begin{array}{l}1+x,-1\le x\le 0\\ 1-x,0<x\le 1\\ \mathrm{0,}-1>x>1\end{array}}$

Expresamos la función F(x) en términos de la función escalón H(x-a)

${\displaystyle F(x)=\left(H(x+1)-H(x)\right)(1+x)+\left(H(x)-H(x-1)\right)(1-x)}$

La solución ψ(x,t) de la ecuación de ondas con la condición inicial F(x) es

${\displaystyle \begin{array}{l}\psi (x,t)=\frac{F(x-ct)+F(x+ct)}{2}=\\ \frac{1}{2}\left\{\begin{array}{l}\left(H(x-ct+1)-H(x-ct)\right)(1+x-ct)+\left(H(x-ct)-H(x-ct-1)\right)(1-x+ct)+\\ \left(H(x+ct+1)-H(x+ct)\right)(1+x+ct)+\left(H(x+ct)-H(x+ct-1)\right)(1-x-ct)\end{array}\right\}\end{array}}$

c=1; %velocidad de propagación
u=@(x,t) (heaviside(x-c*t+1)-heaviside(x-c*t)).*(1+x-c*t)+(heaviside(x-c*t)-
heaviside(x-c*t-1)).*(1-x+c*t);
v=@(x,t) (heaviside(x+c*t+1)-heaviside(x+c*t)).*(1+x+c*t)+(heaviside(x+c*t)-
heaviside(x+c*t-1)).*(1-x-c*t);
psi=@(x,t) (u(x,t)+v(x,t))/2;

tt=[0.25,0.5,1,2]; %tiempos
for i=1:4
    subplot(2,2,i)
    t=tt(i);
    hold on
    f=@(x) u(x,t);
    fplot(f,[-4,4],'color','r', 'lineStyle','--')
    f=@(x) v(x,t);
    fplot(f,[-4,4],'color','b', 'lineStyle','--')
    f=@(x) psi(x,t);
    fplot(f,[-4,4],'color','k')
    hold off
    grid on
    xlabel('x')
    ylabel('\psi')
    title(['t=',num2str(t)])
end

Representamos ψ(x,t) en los instantes t=0.25, 0.5, 1, 2

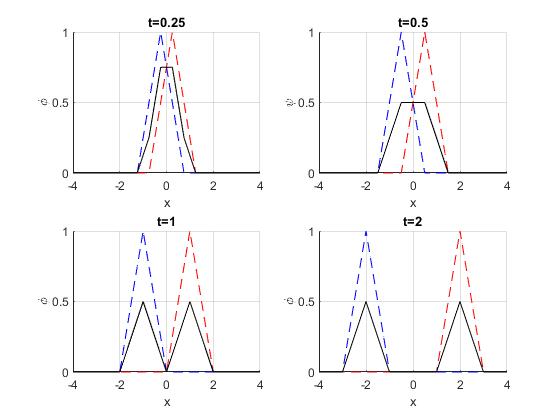
La línea a trazos en color azul muestra F(x+ct), que se propaga hacia la izquierda y en color rojo F(x-ct) que se propaga hacia la derecha. En color negro, el promedio, ψ(x,t)

Solución para una cuerda sin deformar, F(x)=0

Consideremos una cuerda infinita, sin deformar F(x)=0. Los puntos de la cuerda tienen una velocidad inicial G(x). La solución de la ecuación de ondas es

${\displaystyle \begin{array}{l}\psi (x,t)=\frac{1}{2c}{\displaystyle \underset{x-ct}{\overset{x+ct}{\int }}G(s)ds}=\frac{1}{2}\left(g(x+ct)-g(x-ct)\right)\\ g(x)=\frac{1}{c}{\displaystyle \underset{x_0}{\overset{x}{\int }}G(s)ds}\end{array}}$

Ejemplo 1

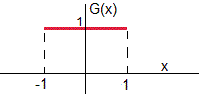
Sea

${\displaystyle G(x)=\{\begin{array}{l}0-\infty <x<-1\\ 1-1\le x\le 1\\ 01<x<\infty \end{array}}$

Calculamos g(x)

${\displaystyle g(x)=\frac{1}{c}{\displaystyle \underset{-\infty }{\overset{x}{\int }}G(s)ds=\frac{1}{c}\{\begin{array}{l}\mathrm{0,}-\infty <x<-1\\ {\displaystyle \underset{-1}{\overset{x}{\int }}1·dx=x+\mathrm{1,}-1\le x\le 1}\\ {\displaystyle \underset{-1}{\overset{1}{\int }}1·dx=2=\mathrm{2,}1<x<\infty }\end{array}}}$

Expresamos la función g(x) en términos de la función escalón H(x-a)

${\displaystyle \begin{array}{l}g(x)=\frac{1}{c}\left\{\left(H(x+1)-H(x-1)\right)(x+1)+2H(x-1)\right\}=\\ \frac{1}{c}\left\{H(x+1)(x+1)-H(x-1)(x-1)\right\}\end{array}}$

La solución ψ(x,t) de la ecuación de ondas con la condición inicial G(x) es

${\displaystyle \begin{array}{l}\psi (x,t)=\frac{1}{2}\left(g(x+ct)-g(x-ct)\right)=\\ \frac{1}{2c}\left\{\begin{array}{l}H(x+ct+1)(x+ct+1)-H(x+ct-1)(x+ct-1)\\ -H(x-ct+1)(x-ct+1)+H(x-ct-1)(x-ct-1)\end{array}\right\}\end{array}}$

Representamos ψ(x,t) en los instantes t=0.25, 0.5, 1, 2

c=1; %velocidad de propagación
g=@(x) (heaviside(x+1).*(x+1)-heaviside(x-1).*(x-1))/c;
psi=@(x,t) (g(x+c*t)-g(x-c*t))/2;

tt=[0.25,0.5,1,2]; %tiempos
for i=1:4
    subplot(2,2,i)
    t=tt(i);
    fplot(@(x) psi(x,t),[-4,4],'color','k')
    grid on
    xlabel('x')
    ylabel('\psi')
    title(['t=',num2str(t)])
end

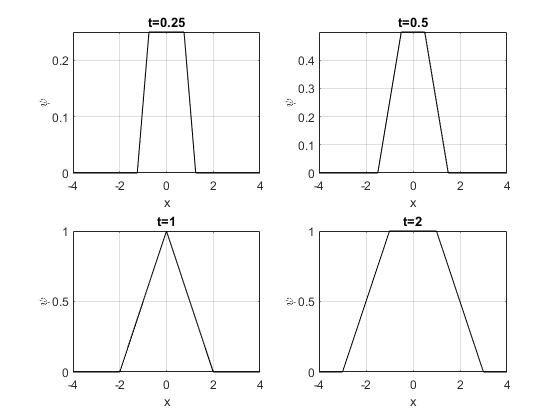
En la animación, la línea a trazos en color azul, se muestra g(x+ct), que se propaga hacia la izquierda y en color rojo -g(x-ct) que se propaga hacia la derecha. En color negro, el promedio ψ(x,t)

Ejemplo 2

Sea

${\displaystyle G(x)=\frac{1}{a}\exp \left(-\frac{\left|x\right|}{a}\right)}$

Calculamos la integral g(x)

${\displaystyle g(x)=\frac{1}{c}{\displaystyle \underset{-\infty }{\overset{x}{\int }}G(s)ds=\frac{1}{ca}}\{\begin{array}{l}{\displaystyle \underset{-\infty }{\overset{x}{\int }}{e}^{s/a}ds=a{e}^{x/a},-\infty <x<0}\\ {\displaystyle \underset{-\infty }{\overset{0}{\int }}{e}^{s/a}ds+{\displaystyle \underset{0}{\overset{x}{\int }}{e}^{-s/a}ds=a+\left(-a{e}^{-x/a}+a\right)=2a-a{e}^{-x/a},0<x<\infty }}\end{array}}$

La solución ψ(x,t) es

${\displaystyle \begin{array}{l}g(x+ct)=\frac{1}{c}\{\begin{array}{l}{e}^{(x+ct)/a},-\infty <x<-ct\\ 2-e^{-(x+ct)/a},-ct<x<\infty \end{array}\\ g(x-ct)=\frac{1}{c}\{\begin{array}{l}{e}^{(x-ct)/a},-\infty <x<ct\\ 2-e^{-(x-ct)/a},ct<x<\infty \end{array}\\ \psi (x,t)=\frac{1}{2}\left(g(x+ct)-g(x-ct)\right)=\frac{1}{2c}\{\begin{array}{l}{e}^{(x+ct)/a}-e^{(x-ct)/a},-\infty <x<-ct\\ 2-e^{-(x+ct)/a}-e^{(x-ct)/a},-ct<x<ct\\ e^{-(x-ct)/a}-e^{-(x+ct)/a},ct<x<\infty \end{array}\end{array}}$

Representamos ψ(x,t) en los instantes t=0.25, 0.5, 1, 2

c=1; %velocidad de propagación
a=0.7; %parámetro
g=@(x) ((1-heaviside(x)).*exp(x/a)+heaviside(x).*(2-exp(-x/a)))/c;
psi=@(x,t) (g(x+c*t)-g(x-c*t))/2;

tt=[0.25,0.5,1,2]; %tiempos
for i=1:4
    subplot(2,2,i)
    t=tt(i);
    fplot(@(x) psi(x,t),[-5,5],'color','k')
    grid on
    xlabel('x')
    ylabel('\psi')
    title(['t=',num2str(t)])
end

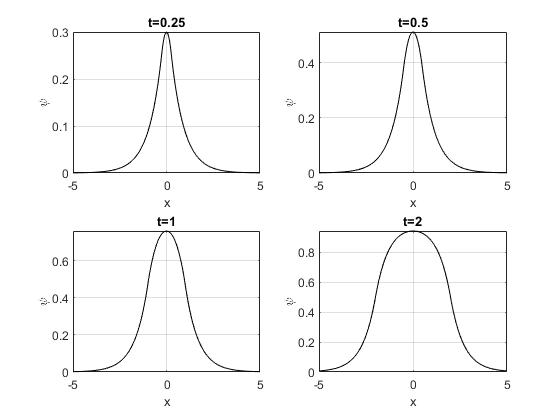
En la animación, en color azul, se muestra g(x+ct), que se propaga hacia la izquierda y en color rojo -g(x-ct) que se propaga hacia la derecha. En color negro, el promedio ψ(x,t). Se ha tomado un valor de a=0.7

Cuerda semi-infinita

Sea una cuerda que se extiende a lo largo de la parte positiva del eje X, 0≤x<∞. En la figura, vemos como un pulso (en color rojo) que se propaga hacia la izquierda se refleja en x=0.

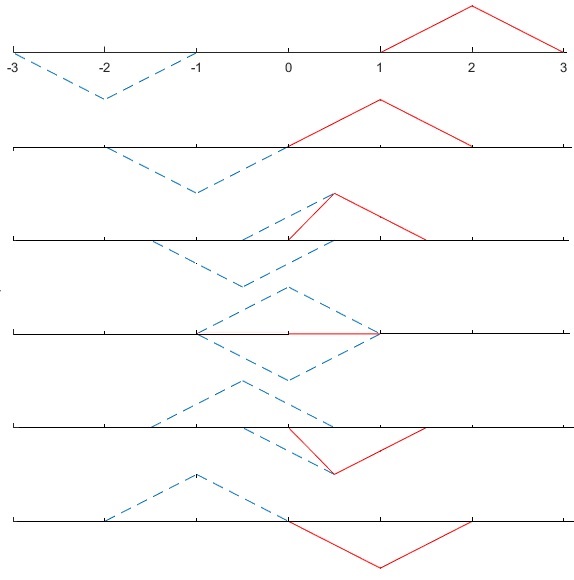
Velocidad inicial nula, G(x)=0

En este caso, la solución de d'Alambert se escribe

${\displaystyle \psi (x,t)=\{\begin{array}{l}\frac{F(x-ct)+F(x+ct)}{2},x\ge ct\\ \frac{F(x-ct)-F(-x+ct)}{2},x<ct\end{array}}$

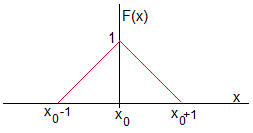
La deformación inicial F(x) de la cuerda alrededor de x₀>0, se muestra en la figura

${\displaystyle F(x)=\{\begin{array}{l}1+x-x_0,x_0-1\le x\le x_0\\ 1-x+x_0,x_0<x\le x_0+1\\ \mathrm{0,}{x}_0-1>x>x_0+1\end{array}}$

La posición inicial del pulso es x₀=2, la velocidad de propagación c=1. Representamos ψ(x,t) en los instantes t=1, 1.5, 2, 3

c=1; %velocidad de propagación
x0=2; %posición inicial
f=@(x) (heaviside(x-x0+1)-heaviside(x-x0)).*(1+x-x0)+
(heaviside(x-x0)-heaviside(x-x0-1)).*(1-x+x0);
psi1=@(x,t) (f(x+c*t)+f(x-c*t))/2;
psi2=@(x,t) (f(x+c*t)-f(c*t-x))/2;

tt=[1,1.5,2, 3]; %tiempos
for i=1:4
    subplot(2,2,i)
    t=tt(i);
    psi=@(x) (x>c*t).*psi1(x,t)+(x<=c*t).*psi2(x,t);    
    fplot(@(x) psi(x),[0,7],'color','k')
    grid on
    xlabel('x')
    ylim([-0.55,0.55])
    ylabel('\psi')
    title(['t=',num2str(t)])
end

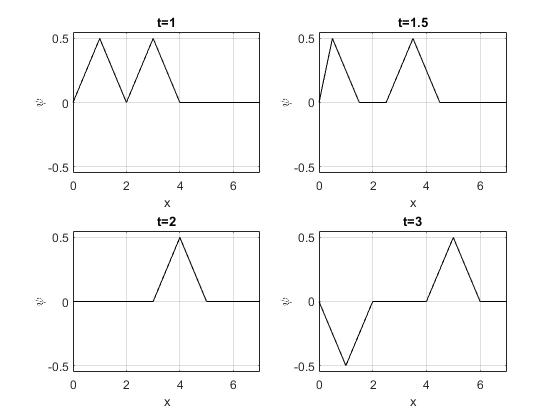
En la animación, se muestra como se propaga un pulso que parte de x₀=5 y se refleja en el extremo x=0 de la cuerda

Deformación inicial nula, F(x)=0

La cuerda está inicialmente sin deformar, pero se le poporciona una velocidad inicial de una unidad a puntos alrededor de x₀, tal como se muestra en la figura (arriba)

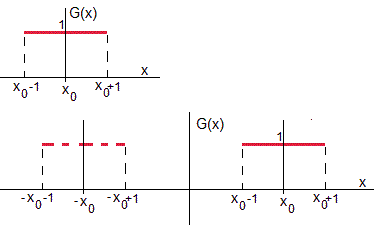
Para una cuerda semi-infinita, sustituimos G(x) por la extensión simétrica de G(x) tal como se muestra en la figura inferior (línea roja a trazos)

${\displaystyle g(x)=\frac{1}{c}{\displaystyle \underset{-\infty }{\overset{x}{\int }}G(s)ds=\frac{1}{c}\{\begin{array}{l}\mathrm{0,}-\infty <x<-x_0-1\\ {\displaystyle \underset{-x_0-1}{\overset{x}{\int }}G(s)·ds=x+x_0+\mathrm{1,}-x_0-1\le x\le -x_0+1}\\ {\displaystyle \underset{-x_0-1}{\overset{-x_0+1}{\int }}G(s)·ds=\mathrm{2,}-x_0+1\le x\le x_0-1}\\ {\displaystyle \underset{-x_0-1}{\overset{x}{\int }}G(s)·ds={\displaystyle \underset{-x_0-1}{\overset{-x_0+1}{\int }}1·ds+}{\displaystyle \underset{x_0-1}{\overset{x}{\int }}1·ds=3+x-x_0}{x}_0-1\le x\le x_0+1}\\ {\displaystyle \underset{-x_0-1}{\overset{x}{\int }}G(s)·ds={\displaystyle \underset{-x_0-1}{\overset{-x_0+1}{\int }}1·ds+}{\displaystyle \underset{x_0-1}{\overset{x_0+1}{\int }}1·ds=}\mathrm{4,}{x}_0+1\le x\le \infty }\end{array}}}$

Expresamos la función g(x) en términos de la función escalón H(x-a)

${\displaystyle \begin{array}{l}g(x)=\left(H(x+x_0+1)-H(x+x_0-1)\right)\left(x+x_0+1\right)+2\left(H(x-x_0-1)-H(x-x_0+1)\right)+\\ \left(H(x-x_0+1)-H(x-x_0-1)\right)\left(3+x-x_0\right)+4H(x-x_0-1)\end{array}}$

La solución ψ(x,t) de la ecuación de ondas con la condición inicial extendida G(x) es

${\displaystyle \psi (x,t)=\frac{g(x+ct)-g(x-ct)}{2}}$

Representamos ψ(x,t) en los instantes t=1, 2, 2.5, 4

c=1; %velocidad de propagación
x0=2; %posición inicial
g=@(x) (heaviside(x+x0+1)-heaviside(x+x0-1)).*(1+x+x0)+
2*(heaviside(x+x0-1)-heaviside(x-x0+1))+(heaviside(x-x0+1)-
heaviside(x-x0-1)).*(3+x-x0)+4*heaviside(x-x0-1);
psi=@(x,t) (g(x+c*t)-g(x-c*t))/2;

tt=[1,2, 2.5, 4]; %tiempos
for i=1:4
    subplot(2,2,i)
    t=tt(i);
    fplot(@(x) psi(x,t),[0,7],'color','k')
    grid on
    ylim([0,2.05])
    xlabel('x')
    ylabel('\psi')
    title(['t=',num2str(t)])
end

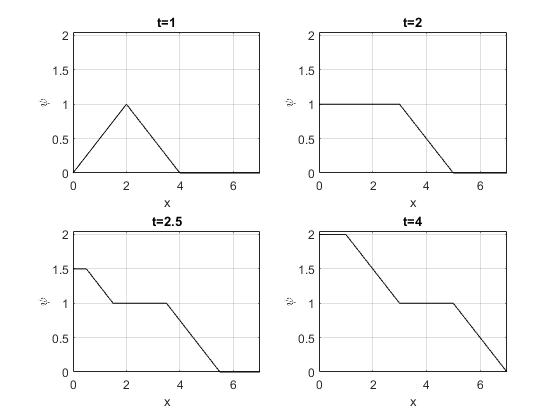
En la animación, se muestra la propagación de un pulso que parte de x₀=5 y se refleja en el extremo x=0 de la cuerda

Cuerda finita

En este apartado, vamos a estudiar la solución d'Alembert de la ecuación de onda de una cuerda punzada y de una cuerda percutida y las vamos a comparar con la solución de la ecuación de onda como de superposición de armónicos.

Velocidad inicial nula, G(x)=0

Sea una cuerda de longitud l, punzada. Las condiciones iniciales son

${\displaystyle \begin{array}{l}\psi (x\mathrm{,0})=\{\begin{array}{l}\frac{h}{a}x0\le x\le a\\ \frac{h}{l-a}(l-x)a<x\le l\end{array}\hfill \\ {\frac{\partial \psi (x,t)}{\partial x}|}_{t=0}=0\hfill \end{array}}$

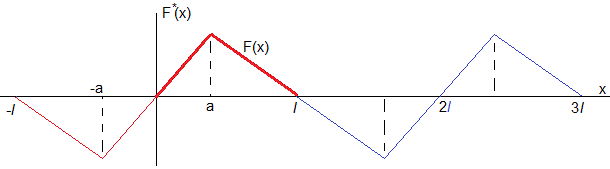
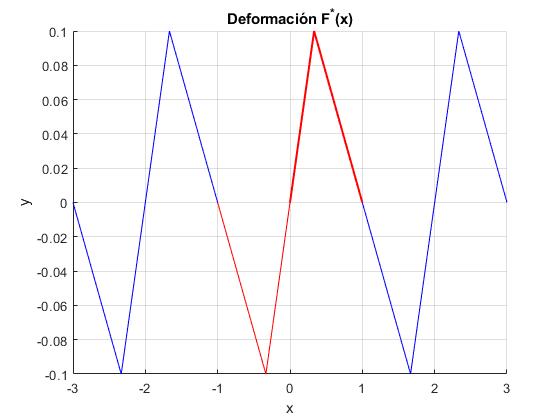
La línea de color rojo gruesa, muestra el desplazamiento inicial de los puntos de la cuerda F(x) de longitud l finita. Construimos la extensión antisimétrica -F(-x) (en color rojo fino). Copiamos F(x) y su extensión (color rojo) a uno y otro lado (color azul) infinitas veces. El estado inicial de la cuerda infinita equivalente es una función F^*(x) de dominio infinito y periodo 2l

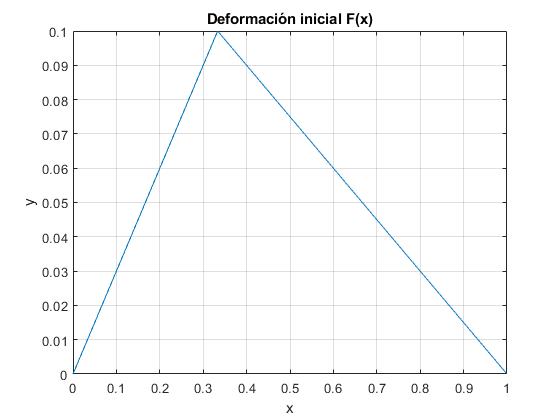
Con este código representamos la deformación inicial de la cuerda de longitud l. La cuerda se desplaza h desde la posición a, tal como se indica en la figura

L=1; %longitud de la cuerda
c=1; %velocidad de propagación
h=0.1; %deformación máxima
a=L/3; %punto de máxima deformación
%deformación inicial de la cuerda
f=@(x) h*(heaviside(x)-heaviside(x-a)).*x/a+h*(heaviside(x-a)-
heaviside(x-L)).*(L-x)/(L-a);
fplot(f,[0,L])
grid on
xlabel('x')
ylabel('y')
title('Deformación inicial F(x)')

Con este código dibujamos la extensión antisimétrica de F(x) y la función F^*(x) de dominio infinito y periodo 2l. En la página titulada Otras funciones se explica como se representa una función periódica

L=1; %longitud de la cuerda
c=1; %velocidad de propagación
h=0.1; %deformación máxima
a=L/3; %punto de máxima deformación
f=@(x) -h*(heaviside(x+L)-heaviside(x+a)).*(x+L)/(L-a)+
h*(heaviside(x+a)-heaviside(x)).*x/a+h*(heaviside(x)-heaviside(x-a)).*x/a+
h*(heaviside(x-a)-heaviside(x-L)).*(L-x)/(L-a);
pf=@(x) f(x-2*floor((x+L)/2)); %función periódica
hold on
fplot(pf,[-3*L,3*L],'color','b') %F*(x)
fplot(f,[0,L],'color','r','lineWidth',1.5) %F(x)
fplot(f,[-L,0],'color','r') %antisimétrica
hold off
grid on
xlabel('x')
ylabel('y')
title('Deformación F^*(x)')

La solución de la ecuación de onda con velocidad inicial G(x)=0, nula es

${\displaystyle $ \psi (x,t)=\frac{F^{*}(x-ct)+F^{*}(x+ct)}{2},0\le x\le l$}$

La solución de la ecuación de onda con la superposición de armónicos de una cuerda punzada es

${\displaystyle \psi (x,t)=\frac{2h{l}^2}{{\pi }^{2}a(l-a)}{\displaystyle \sum _{n=1}^{\infty }\frac{1}{n^2}\sin \left(n\pi \frac{a}{l}\right)\sin \left(n\pi \frac{x}{l}\right)\cos \left(n\pi \frac{ct}{l}\right)}}$

Sea una cuerda de

• longitud. L=1
• la velocidad de propagación, c=1
• máxima deformación inicial, h=0.1
• posición de la máxima deformación, a=L/3

Comparamos ambas soluciones en el instante t=1/2.

L=1; %longitud de la cuerda
c=1; %velocidad de propagación
h=0.1; %deformación máxima
a=L/3; %punto de máxima deformación

%solución d'Alembert
f=@(x) -h*(heaviside(x+L)-heaviside(x+a)).*(x+L)/(L-a)+
h*(heaviside(x+a)-heaviside(x)).*x/a+h*(heaviside(x)-heaviside(x-a)).*x/a+
h*(heaviside(x-a)-heaviside(x-L)).*(L-x)/(L-a);
pf=@(x) f(x-2*floor((x+L)/2)); %periódica
psi=@(x,t) (pf(x-c*t)+pf(x+c*t))/2; %solución d'Alembert
t=1/2; %instante
hold on
fplot(@(x) psi(x,t),[0,1])

%superposición de armónicos, 
x=linspace(0,L,200);
yy=zeros(1,length(x));
for n=1:20 
    yy=yy+sin(n*pi*a/L)*sin(n*pi*x/L)*cos(n*pi*t/L)/n^2;
end
yy=yy*(2*h*L^2/(pi^2*a*(L-a)));
plot(x,yy)
hold off
grid on
xlabel('x')
ylabel('y')
title('Cuerda punzada')

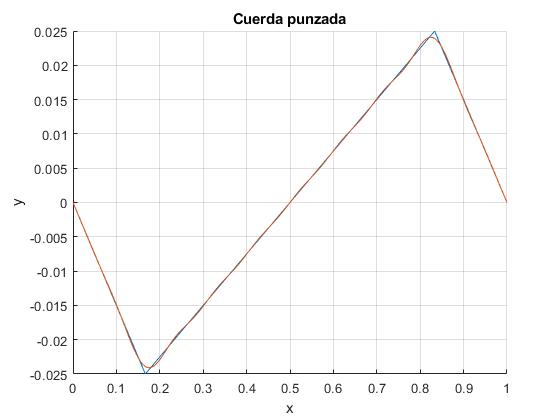
La superposición de armónicos da lugar a una serie infinita convergente, basta un número relativamente pequeño de términos para respresentar el estado de la cuerda en un instante dado t. Por tanto, esta solución de la ecuación de onda es aproximada, mientras que la solución de d'Alembert es exacta

Se introduce

• La posición a de máximo desplazamiento inicial de la cuerda, en el control titulado Cociente a/l
• Se ha fijado el máximo desplazamiento h=0.1, la longitud de la cuerda l=1 y la velocidad de propagación de las ondas en la cuerda c=1

Se pulsa el botón titulado Nuevo

Se suelta la cuerda y se observa su movimiento, en la parte superior se proporciona el dato del tiempo t

Se compara la solución exacta (en rojo, línea gruesa) con la aproximada (en azul, línea fina)

Deformación inicial nula, F(x)=0

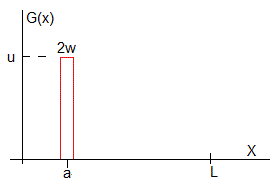
Una cuerda sin deformar en el instante t=0, ψ(x,0)=0, se golpea con un martillo de ancho 2w<<L situado entre las abscisas x=a-w y x=a+w que comunica un impulso inicial a este segmento de cuerda. En estas condiciones, la velocidad de cada punto de la cuerda al instante t=0 esta dada por la función de la figura

${\displaystyle \begin{array}{l}{\frac{\partial \psi (x,t)}{\partial t}|}_{t=0}=\{\begin{array}{l}0x<a-wx>a+w\\ ua-w\le x\le a+w\end{array}\\ \psi (x\mathrm{,0})=0\end{array}}$

Creamos la extensión antisimétrica de G(x)

${\displaystyle g(x)=\frac{1}{c}{\displaystyle \underset{-L}{\overset{x}{\int }}G(s)ds=\frac{1}{c}\{\begin{array}{l}\mathrm{0,}-L<x<-a-w\\ {\displaystyle \underset{-a-w}{\overset{x}{\int }}-u·dx=-u(x+a+w),-a-w<x<-a+w}\\ {\displaystyle \underset{-a-w}{\overset{-a+w}{\int }}-u·dx}+{\displaystyle \underset{-a+w}{\overset{x}{\int }}0·dx=-2uw,a-w\le x\le a+w}\\ -2uw+{\displaystyle \underset{a-w}{\overset{x}{\int }}u·dx=u(x-a-w),a-w<x<a+w}\\ -2uw+{\displaystyle \underset{a-w}{\overset{a+w}{\int }}u·dx+{\displaystyle \underset{a+w}{\overset{x}{\int }}0·dx=\mathrm{0,}a+w<x<L}}\end{array}}}$

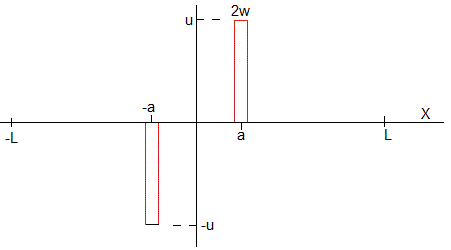
Expresamos esta función en términos de la la función escalón

${\displaystyle g(x)=\frac{1}{c}\left\{\begin{array}{l}-u(x+a+w)\left(H(x+a+w)-H(x+a-w)\right)-2uw\left(H(x+a-w)-H(x-a+w)\right)\\ +u(x-a-w)\left(H(x-a+w)-H(x-a-w)\right)\end{array}\right\}}$

Creamos la función g^*(x) de dominio infinito y periodo 2l

La solución de la ecuación de onda con deformación inicial nula F(x)=0, es

${\displaystyle \psi (x,t)=\frac{1}{2}\left(g^{*}(x+ct)-g^{*}(x-ct)\right),0\le x\le l}$

La solución de la ecuación de onda con la superposición de armónicos de una cuerda precutida es

${\displaystyle \psi (x,t)=\frac{4ul}{{\pi }^{2}c}{\displaystyle \sum _{n=1}^{\infty }\frac{1}{n^2}\sin \left(n\pi \frac{w}{l}\right)\sin \left(n\pi \frac{a}{l}\right)\sin \left(n\pi \frac{x}{l}\right)\sin \left(n\pi \frac{c}{l}t\right)}}$

Sea una cuerda de

• longitud. L=1
• la velocidad de propagación, c=0.2
• la anchura del impacto, 2w=2·0.1
• velocidad del impacto, u=1
• la posición del impacto, a=0.2

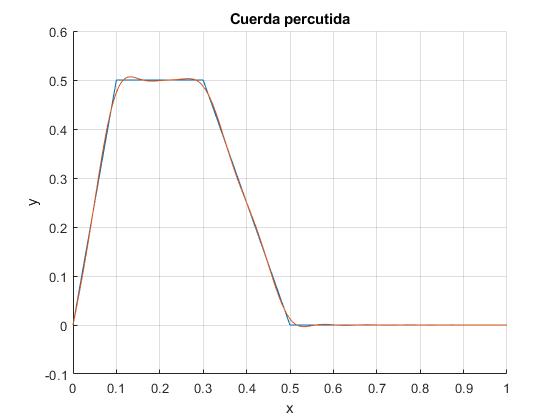
Comparamos ambas soluciones en el instante t=1.

L=1; %longitud de la cuerda
u=1; %velocidad
a=0.2; %posición percusión
w=0.1; %anchura es 2w
c=0.2; %velocidad de propagación

%solución d'Alembert
g=@(x) (-u*(heaviside(x+a+w)-heaviside(x+a-w)).*(x+a+w)-
2*u*w*(heaviside(x+a-w)-heaviside(x-a+w))
+u*(heaviside(x-a+w)-heaviside(x-a-w)).*(x-a-w))/c;
pg=@(x) g(x-2*floor((x+L)/2)); %función periódica
psi=@(x,t) (pg(x+c*t)-pg(x-c*t))/2;
t=1; %instante
hold on
fplot(@(x) psi(x,t),[0,L])

%superposición de armónicos
x=linspace(0,L,200);
yy=zeros(1,length(x));
for n=1:20 
    yy=yy+sin(n*pi*w/L)*sin(n*pi*a/L)*sin(n*pi*x/L)*sin(n*pi*c*t/L)/n^2;
end
yy=yy*4*u*L/(pi^2*c);
plot(x,yy)
hold off

grid on
xlabel('x')
ylabel('y')
title('Cuerda percutida')

Se introduce

• La posición a, en el control titulado Cociente a/l
• La anchura 2w del percutor, en el control titulado Anchura pulso w
• Se ha fijado la velocidad u=1 del percutor, la longitud de la cuerda l=1 y la velocidad de propagación de las ondas en la cuerda c=0.2

Se pulsa el botón titulado Nuevo

Se observa el movimiento de la cuerda, en la parte superior se proporciona el dato del tiempo t

Se compara la solución exacta (en rojo, línea gruesa) con la aproximada (en azul, línea fina)

Referencias

A. Salih. Second-Order Wave Equation. Indian Institute of Space Science and Technology, Thiruvananthapuram. 23 December 2016. https://www.iist.ac.in/sites/default/files/people/IN08026/dAlembert.pdf

B. M. Budak, A. A. Samarski, A. N. Tijonov. Problemas de la Física Matemática. Tomo I. Editorial Mir. (1984). Problemas 59 y 60. Enunciado, pág. 26; solución, págs. 140-143

Nakhlé H. Asmar. Partial Differential Equations with Fourier Series and Boundary Value Problems. Second edition. Pearson, Prentice Hall, 2005. pp. 127-130