Una bolita sobre una plataforma que describe un MAS

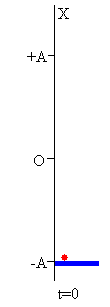
La plataforma describe un MAS de frecuencia ω angular. En el instante t=0 parte del reposo desde la posición x=-A, siendo A la amplitud de la oscilación

${\displaystyle \begin{array}{l}x=A\sin (\omega t+\phi )\hfill \\ v=\frac{dx}{dt}=A\omega \cos (\omega t+\phi )\hfill \end{array}}$

en el instante t=0, la posición y velocidad inicial son, respectivamente,

-A=Asinφ
0=Aωcosφ

De las condiciones iniciales, despejamos la fase inicial φ=-π/2

La ecuación del MAS se escribe

x=A·sin(ωt-π/2)=-A·cos (ωt)

 Derivando con respecto al tiempo obtenemos las expresiones de la velocidad y aceleración.

v=A·ωsin (ωt)

a=A·ω²cos(ωt)=-ω²x

Fuerzas sobre la bolita

Cuando la plataforma se encuentra en la posición x las fuerzas sobre la bolita que descansa en la plataforma son

• El peso, mg
• La reacción o fuerza que ejerce la plataforma, N

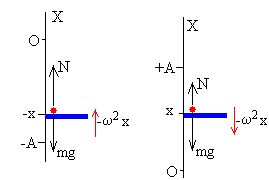
• Cuando la plataforma está por debajo del origen x<0, (figura de la izquierda) la aceleración a es positiva

La segunda ley de Newton se escribe

N-mg=-mω²x
N=mg-mω²x

Como x<0  la reacción N es siempre mayor que el peso

• Cuando la plataforma está por encima del origen x>0, (figura de la derecha) la aceleración a es negativa

La segunda ley de Newton se escribe

N-mg=-mω²x
N=mg-mω²x

Como x>0  la reacción N es siempre menor que el peso

La máxima aceleración se produce cuando la plataforma alcanza el punto de retorno x=A. La bolita permanecerá sobre la plataforma siempre que N>0, es decir siempre que

mg> mω²A o bien, que g>ω²A

Cuando N se hace cero la bolita deja de estar en contacto con la plataforma, esto se produce en la posición x₀>0 tal que

g=ω²x₀

En el instante t₀ tal que

${\displaystyle \frac{g}{{\omega }^2}=-A\cos (\omega t_0)}$

La velocidad de la plataforma y la inicial de la bolita son

v₀=A·ωsin (ωt₀)

La bolita se mueva baja la acción de la aceleración constante de la gravedad.

${\displaystyle y=x_0+v_0(t-t_0)-\frac{1}{2}g{\left(t-t_0\right)}^2}$

La bolita chocará repetidamente con la plataforma

Ejemplo.

Sea la amplitud A=0.1, la bolita se desprende de la plataforma si la frecuencia angular ω es mayor que ω_c o el periodo P<P_c.

${\displaystyle \begin{array}{l}{\omega }_c=\sqrt{\frac{g}{A}}{\omega }_c=\sqrt{\frac{9.8}{0.1}}=9.90\text{rad/s}\\ P_c=\frac{2\pi }{{\omega }_c}=0.63\text{s}\end{array}}$

Si el periodo P=0.45 s, la frecuencia angular es ω=13.96 rad/s

La bolita se desprende en la posición x₀=0.05 m

En el instante t₀, tal que

x₀=-0.1cos (ωt₀), t₀=0.15 s

La velocidad inicial de la bolita en dicho instante es

v₀=0.1ωsin (ωt₀)=1.21 m/s

Actividades

Se introduce

• El periodo del MAS que describe la plataforma, en el control titulado Periodo
• La amplitud del MAS de la plataforma se ha fijado en A=0.1 m

Se pulsa el botón titulado Nuevo

Observamos el movimiento de la bolita sobre la plataforma. A la derecha, la gráfica de la posición de la bolita (en color rojo) y de la plataforma (en color azul) en función del tiempo.

A la izquierda, las fuerzas sobre la bolita

• El peso, mg
• La reacción de la plataforma, N

Cuando la fuerza que ejerce la plataforma N se hace cero, la bolita despega de la plataforma.

Un bloque encima de otro unido a un muelle elástico

Un bloque de masa M está unido a un muelle de constante elástica k. Encima de este bloque se coloca otro de masa m. Supondremos que el bloque de masa M desliza sin rozamiento sobre el plano horizontal. Sin embargo, entre las superficies en contacto de ambos bloques hay rozamiento, el coeficiente estático es μ_s.

El sistema formado por los dos bloques y el muelle elástico parte del origen y describe un MAS de amplitud A. Su posición, x, velocidad v, y aceleración a, en función del tiempo t son

${\displaystyle \begin{array}{l}x=A\sin \left(\omega t\right)\omega =\sqrt{\frac{k}{m+M}}\\ v=\frac{dx}{dt}=A\omega \cos \left(\omega t\right)\\ a=\frac{dv}{dt}=-A{\omega }^2\sin \left(\omega t\right)=-{\omega }^{2}x\end{array}}$

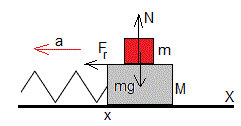
La aceleración a es de sentido contrario al desplazamiento x. Sobre el boque de masa m actúan las siguientes fuerzas:

• El peso, mg
• La reacción N de la superficie de contacto con el bloque de masa M, que es igual al peso
• La fuerza de rozamiento F_r, entre ambas superficies

De acuerdo a la segunda ley de Newton

F_r=m|a|=mω²x

A medida que se incrementa el desplazamiento x de los bloques, la fuerza de rozamiento F_r va aumentando hasta que alcanza el valor máximo μ_sN=μ_smg en la posición x₀

${\displaystyle \begin{array}{l}{\mu }_{s}mg=m{\omega }^2{x}_0\\ x_0=\frac{{\mu }_{s}g}{{\omega }^2}\end{array}}$

A partir del instante t₀ tal que, x₀=Asin(ωt₀), la aceleración del boque de masa m es μ_sg y la aceleración del bloque de masa M es ω²x.

Suponiendo que a partir del instante t₀, los bloques dejan de estar en contacto. El sistema formado por el bloque de masa M y el muelle elástico de constante k, describirá un Movimiento Armónico Simple de distinta frecuencia angular

${\displaystyle \begin{array}{l}x=A_1\sin \left({\omega }_1(t-t_0)+{\phi }_1\right){\omega }_1=\sqrt{\frac{k}{M}}\\ v=\frac{dx}{dt}=A_1{\omega }_1\cos \left({\omega }_1(t-t_0)+{\phi }_1\right)\end{array}}$

Donde la nueva amplitud A₁ y fase inicial φ₁ se calculan a partir de las condiciones iniciales en el instante t₀.

${\displaystyle \begin{array}{l}t=t_0\{\begin{array}{l}{x}_0=A\sin \left(\omega t_0\right)\\ v_0=A\omega \cos \left(\omega t_0\right)\end{array}\\ A_1=\sqrt{x_0^2+{\left(\frac{v_0}{{\omega }_1}\right)}^2}\tan {\phi }_1=\frac{{\omega }_1{x}_0}{v_0}\end{array}}$

Actividades

Se introduce

• La masa M del bloque unido al muelle elástico, en el control titulado Masa M
• La masa del bloque que se coloca encima está fijada en m= 1 kg
• La constante elástica del muelle se ha fijado en k=20 N/m
• El coeficiente estático μ_s de rozamiento entre las superficies en contacto de ambos bloques en el control titulado Coef. rozamiento
• La amplitud del MAS se ha fijado en A=0.9 m

Se pulsa el botón titulado Nuevo

Ejemplo

La masa del bloque M=6 kg, la masa del bloque que se coloca encima m=1 kg. El coeficiente estático μ_s=0.2

La posición en la que el bloque de masa m se cae es

${\displaystyle \begin{array}{l}\omega =\sqrt{\frac{k}{m+M}}=\sqrt{\frac{20}{6+1}}=\sqrt{\frac{20}{7}}\\ {\omega }^2{x}_0={\mu }_{s}g{x}_0=\frac{0.2·9.8}{\frac{20}{7}}=0.686\text{m}\end{array}}$

que corresponde al instante t₀=0.51 s, la velocidad de los bloques es v₀=0.985 m/s

Cuando el bloque de masa m se ha caído, la frecuencia angular es mayor

${\displaystyle {\omega }_1=\sqrt{\frac{k}{M}}=\sqrt{\frac{20}{6}}\text{rad/s}}$

La amplitud A₁ del nuevo MAS es

${\displaystyle A_1=\sqrt{x_0^2+{\left(\frac{v_0}{{\omega }_1}\right)}^2}=\sqrt{{0.686}^2+\frac{{0.985}^2·6}{20}}=0.872\text{m}}$

En color rojo se representa el primer MAS de amplitud A y frecuencia angular ω y en color azul, el segundo MAS de amplitud A₁ y frecuencia angular mayor ω₁

Referencias

Último apartado

Lim Yung-kuo. Problems and Solutions on Mechanics. World Scientific (1994). Problem 1078, pp. 126-127