Tiro parabólico
Movimiento bajo la aceleración constante de la gravedad
Salto de esquí en Innsbruck (Austria), 1-08-2017
Para resolver un problema de tiro parabólico es necesario seguir los pasos:
- Establecer el sistema de referencia, es decir, el origen y los ejes horizontal X, y vertical Y
- Determinar el valor y el signo de la aceleración vertical
- Las componentes de la velocidad inicial (incluido el signo)
- La posición inicial
- Escribir las ecuaciones del movimiento
- A partir de los datos, hallar las incógnitas
En la figura, tenemos un proyectil que se ha disparado con una velocidad inicial v0, haciendo un ángulo θ con la horizontal, las componentes de la velocidad inicial son
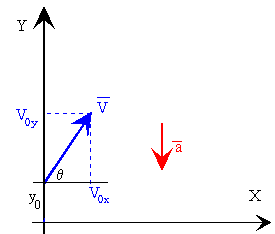
Las ecuaciones del movimiento de un proyectil bajo la aceleración constante de la gravedad son:
Eliminado el tiempo en las ecuaciones que nos dan las posiciones x e y, obtenemos la ecuación de la trayectoria, que tiene la forma y=ax2 +bx +c, lo que representa una parábola.
Tiempo de vuelo, alcance y altura máxima
El tiempo de vuelo y el alcance horizontal se obtienen cuando el cuerpo llega al suelo y=0. La solución positiva de la ecuación de segundo grado es
Obtenemos la altura máxima, cuando la componente vertical de la velocidad vy se hace cero
Cuando el proyectil parte del origen, y0=0
El cálculo del ángulo θ para el cual el alcance es máximo, dX/dθ=0, es un interesante ejercicio de cálculo de derivadas y simplificación de expresiones algebraicas
El resultado final es
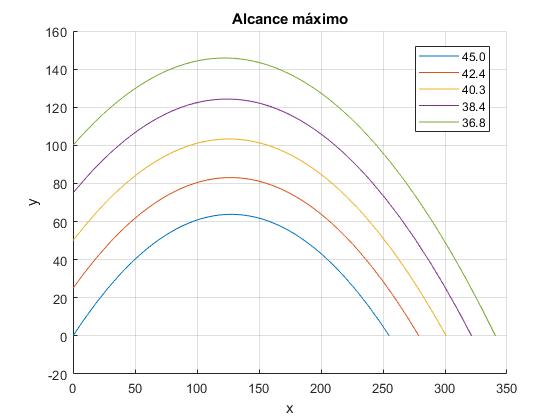
Cuando el proyectil parte del origen y0=0, el alcance máximo se obtiene para el ángulo de 45°. El ángulo θm disminuye a medida que se incrementa la altura inicial de disparo y0, tal como se aprecia en la gráfica
v0=50; %velocidad de disparo
hold on
for y0=[0,25,50,75,100] %altura inicial
th=asin(1/sqrt(2*(1+9.8*y0/v0^2)));
T=v0*sin(th)*(1+sqrt(1+2*9.8*y0/(v0*sin(th))^2))/9.8;
fplot(@(t) v0*cos(th)*t, @(t) y0+v0*sin(th)*t-4.9*t.^2,[0,T],
'displayName',sprintf('%2.1f',th*180/pi))
end
hold off
xlabel('x')
ylabel('y')
legend('-DynamicLegend','location','best')
grid on
title('Alcance máximo')
Ejercicio
Un proyectil es disparado con una velocidad de 600 m/s, haciendo un ángulo de 60º con la horizontal. Tomar g=10 m/s2. Calcular:
- El alcance horizontal.
- La altura máxima
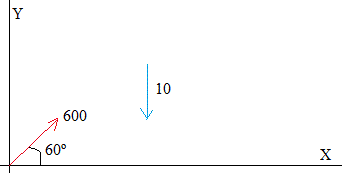
Alcance, y=0
Altura máxima vy=0
>> syms t;
>> tf=solve(300*sqrt(sym('3'))*t-5*t^2)
tf = 0
60*3^(1/2)
>> x=300*tf(2)
x =18000*3^(1/2)
Actividades
Resolver numéricamente los siguientes problemas y comprobar la solución con el programa interactivo
Un avión en vuelo horizontal a una altura de 300 m y con una velocidad de 60 m/s, deja caer una bomba. Calcular el tiempo que tarda en llegar al suelo y el desplazamiento horizontal de la bomba.
- Se lanza un cuerpo desde el origen con velocidad horizontal de 40 m/s y con una velocidad vertical hacia arriba de 60 m/s. Calcular la máxima altura y el alcance horizontal.
Resolver el ejercicio anterior, tomando como lugar de lanzamiento la cima de una colina de 50 m de altura.
Se lanza un proyectil desde una colina de 300 m de altura, con una velocidad horizontal de 50 m/s y una velocidad vertical de -10 m/s (hacia abajo). Calcular el alcance horizontal y la velocidad con que llega al suelo.
Un cañón dispara una bala desde lo alto de un acantilado de 200 m de altura con una velocidad de 46 m/s haciendo un ángulo de 30º por encima de la horizontal. Calcular el alcance, el tiempo de vuelo, y las componentes de la velocidad de la bala al nivel del mar. Hallar también la altura máxima. (Hallar primero, las componentes horizontal y vertical de la velocidad inicial).
Se introduce en los controles de edición
- la altura inicial y0.
- la componente vx de la velocidad inicial
- la componente vy de la velocidad inicial
Se pulsa el botón titulado Nuevo. Se observa el movimiento de de la partícula y la trayectoria que describe. En la parte superior se muestran los valores de su posición x, e, y de su velocidad vx y vy, según va transcurriendo el tiempo t.
Se detiene || la animación cuando se está próximo a alcanzar la máxima altura. Se avanza paso a paso >| hasta alcanzarla vy≈0 y se anota la posición x,y. Se reanuda la animación pulsando ►. Cuando se está próximo a llegar al suelo, se pulsa el botón pausa ||, y se avanza paso a paso >| hasta alcanzar y≈0, se anota el valor del vector velocidad vx, vy y el tiempo t
Saltos de esquí
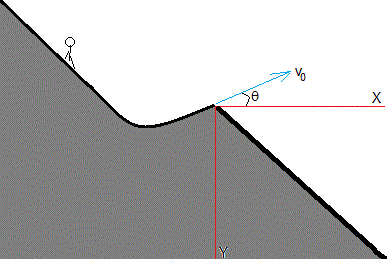
Consideremos un esquiador que baja por una pista y despega con velocidad v0 haciendo una ángulo θ con la horizontal. El esquiador describe una trayectoria parabólica hasta que aterriza en la pista inclinada cuya ecuación es y=mx
Establecemos el origen al final de la pista y los ejes X e Y (hacia abajo) tal como se muestra en la figura. La ecuación de la trayectoria será
Eliminando el tiempo en las ecuaciones de x e y, obtenemos la ecuación de la trayectoria, una parábola
El aterrizaje del esquiador es el punto de intersección entre la recta y=mx y la parábola
Representamos x en función de θ entre -20 y 80°, tomando como velocidad inicial v0=25 m/s
v0=25; %velocidad inicial
m=1; %pendiente de la pista, 45°
f=@(x) 2*v0^2*(m+tan(x*pi/180))*cos(x*pi/180)^2/9.8;
fplot(f,[-20,80])
grid on
xlabel('\theta')
ylabel('x')
title('saltos de esquí')
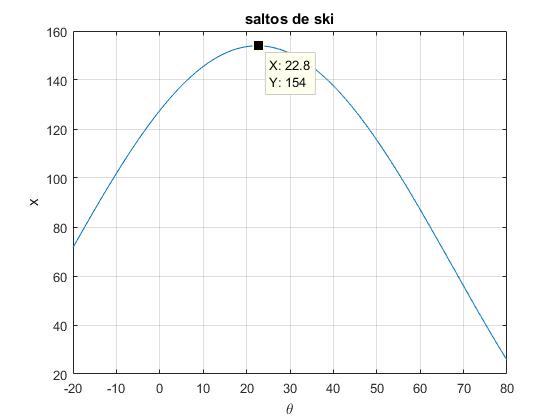
El valor del ángulo θ para el cual x es máximo se obtiene derivando e igualando a cero
Con m=1, el ángulo para el cual el alcance es máximo, θ=22.5°
Desliza sobre el tejado y cae al suelo
En este problema, el ángulo de tiro está por debajo de la horizontal, el alcance también presenta un máximo como en el ejercicio anterior
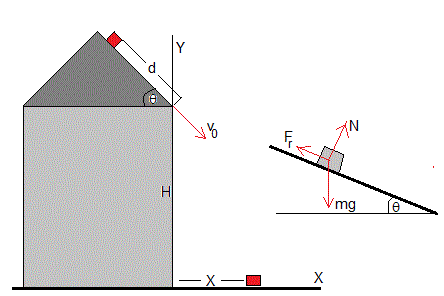
Un objeto de masa m baja deslizando por un tejado inclinado un ángulo θ, recorriendo una distancia d hasta que cae con velocidad v0. Vamos a determinar la distancia X al punto de impacto del objeto en la calle. El coeficiente de rozamiento entre el tejado y el cuerpo es μ.
Cuando el objeto está en el tejado, las fuerzas que actúan son
- El peso, mg
- La reacción N, N=mgcosθ
- La fuerza de rozamiento Fr=μ·N, cuando el cuerpo desliza
La ecuación del movimiento del objeto a lo largo del tejado se escribe, ma=mgsinθ-μmgcosθ
El cuerpo empieza a deslizar (a=0) cuando el tejado tiene una inclinación tal que tanθ=μ
La velocidad v0 del objeto cuando llega al alero es
Las ecuaciones del movimiento del objeto en el aire son
El alcance X se calcula cuando llega al suelo, y=0
mu=0.2;
aCritico=atan(mu); %empieza a deslizar
H=10;
d=5;
v0=@(x) sqrt(sin(x)-mu*cos(x));
f=@(x) 2*(v0(x).*cos(x)).*(-v0(x).*sin(x)+sqrt((v0(x).*sin(x)).^2+H));
fplot(f,[aCritico,80*pi/180])
set(gca,'XTick',0:pi/12:pi/2)
set(gca,'XTickLabel',{'0','\pi/12','\pi/6','\pi/4','\pi/3','5\pi/12','\pi/2'})
grid on
xlabel('\theta')
ylabel('X')
title('Alcance')
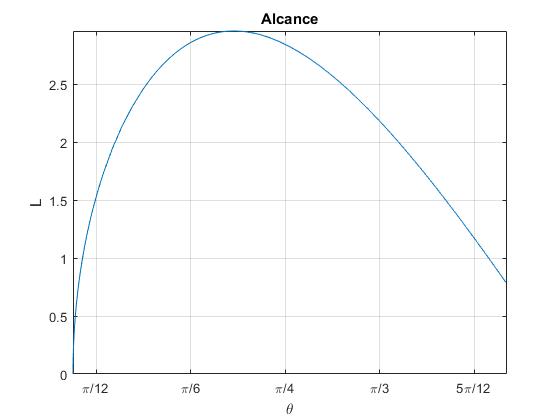
Dispositivo para lanzar proyectiles
Una rampa
Se lanza un proyectil de masa m con velocidad vp desde la base de un plano inclinado de longitud l y ángulo θ.
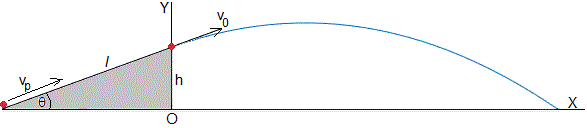
El proyectil desliza sin rozamiento, alcanzando el punto más alto de la rampa con velocidad v0. Aplicando el principio de conservación de la energía
A continuación, el proyectil describe un tiro parabólico con velocidad de disparo v0 y ángulo de tiro θ. La posición del proyectil respecto al sistema de referencia OXY es
El tiempo de vuelo (y=0) es
El alcance horizontal es
El alcance horizontal es función de la velocidad de disparo v0, que a su vez, es función de la longitud de la rampa l
El alcance es máximo
La derivada dR/dl es nula para θ=π/2, una rampa vertical, que no tiene sentido
La derivada es también nula cuando
La solución correcta es
La otra, con signo +, no cumple la ecuación original
La longitud lm de la rampa que produce alcance R máximo es
Representamos la función
f=@(x) (1-2*sin(x))./(sin(x).*(1-sin(x)));
fplot(f, [10*pi/180,40*pi/180])
grid on
set(gca,'XTick',0:pi/12:pi/6)
set(gca,'XTickLabel',{'0','\pi/12','\pi/6'})
xlabel('\theta')
ylabel('f(\theta)')
title('Longitud de la rampa')
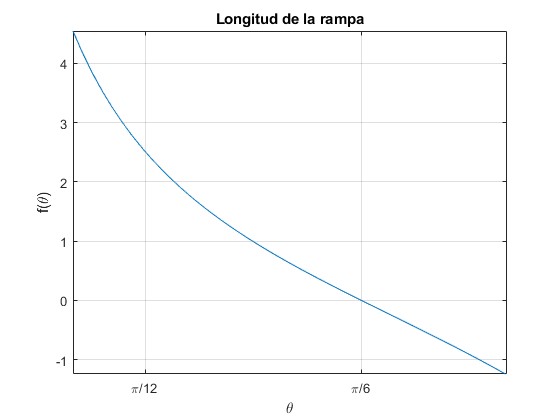
En la gráfica observamos que lm≤0 para θ>π/6 (30°). La rampa solamente tiene algún efecto para ángulos de tiro θ<30°
El alcance máximo es
El alcance sin rampa (vp es la velocidad de disparo y θ el ángulo de tiro)
Representamos las funciones
f=@(x) cos(x)./(2*(1-sin(x)));
hold on
fplot(f, [0,pi/6])
g=@(x) sin(2*x);
fplot(g, [0,pi/6])
hold off
grid on
set(gca,'XTick',0:pi/12:pi/6)
set(gca,'XTickLabel',{'0','\pi/12','\pi/6'})
legend('con rampa','sin rampa','location','best')
xlabel('\theta')
ylabel('R')
title('Alcance')
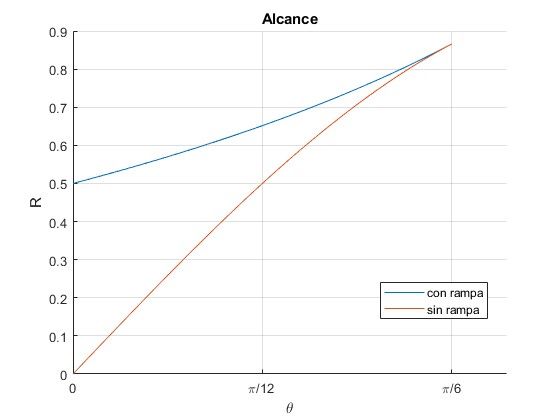
Los disparos con rampa son ventajosos para ángulos de la rampa θ<30°
Un muelle comprimido
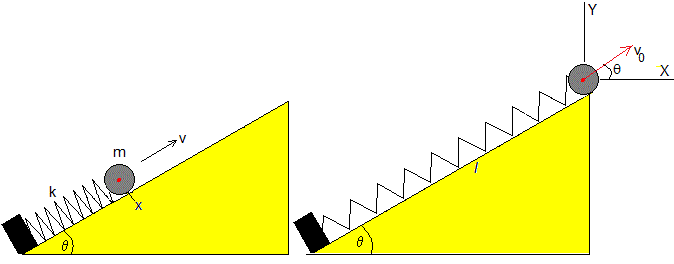
Supongamos que disponemos de un dispositivo para lanzar proyectiles tal como se muestra en la figura. Una bola de masa m comprime un muelle elástico de constante k tal como se aprecia a la izquierda de la figura. Cuando se libera la bola, incrementa su velocidad hasta que el muelle recupera su longitud l sin deformar (a la derecha de la figura).
Si despreciemos el rozamiento, aplicamos el principio de conservación de la energía para calcular la velocidad final v0 de la bola. La energía potencial elástica almacenada en el muelle, se convierte en energía potencial correspondiente a la altura lsinθ y en energía cinética
El alcance de un proyectil que parte del origen con velocidad v0, haciendo un ángulo θ con la horizontal es
donde f=kl/mg es el cociente entre la máxima fuerza que ejerce el muelle y el peso.
Demostramos que el alcance máximo se obtiene para el ángulo θm=45°. En este caso, la velocidad inicial v0 depende del ángulo θ, por lo que el alcance máximo ya no se produce para esta ángulo sino para otro menor.
Dado f, resolvemos la ecuación transcendente utilizando la función
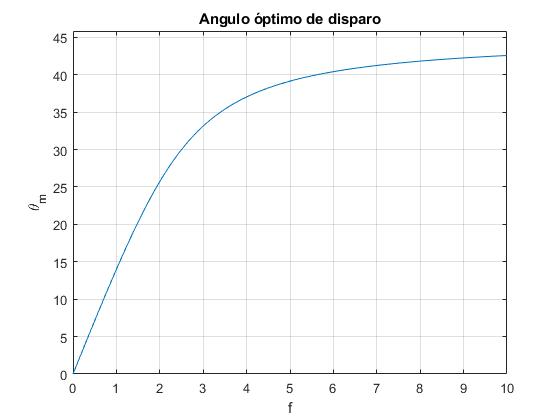
Representamos el θm en función de f. Observamos que cuando f se hace grande, θm tiende hacia 45°. El peso del proyectil mg afecta al alcance X y tiene poco efecto cuando es pequeño en comparación con la máxima fuerza kl que ejerce el muelle.
ff=linspace(0,10,50);
th=zeros(1,length(ff));
i=1;
for f=ff
g=@(x) cos(2*x)*(f-2*sin(x))-sin(2*x)*cos(x);
th(i)=fzero(g,[0,pi/4]);
i=i+1;
end
plot(ff,th)
set(gca,'YTick',0:5*pi/180:pi/4)
set(gca,'YTickLabel',{'0','5','10','15','20','25','30','35','40','45'})
xlabel('f')
ylabel('\theta_m')
grid on
title('Angulo óptimo de disparo')
Referencias
Krzystof Rebilas. Optimal Ski Jump. The Physics Teacher. Vol. 51, February 2013, 108-109
Willem H. van den Berg, Andrea R. Burbank. Sliding off a Roof: How Does the Landing Point Depend on the Steepness?. The Physics Teacher. Vol. 40, February 2002, 84-85
Yuji Kajiyama. Maximizing the Range of a Projectile from Takeoff Ramp. Lat. Am. J. Phys. Educ. Vol. 14, No. 2, June 2020
David L. Herrick. The Effect of Projectile Weight on the Optimum Launch Angle and Range. The Physics Teacher. Vol. 56. December 2018. pp. 584-585

