Choque inelástico bala-disco
Una bala de 0.2 kg y velocidad horizontal de 120 m/s, choca contra un pequeño diente situado en la periferia de un volante de masa 1.5 kg y 12 cm de radio, empotrándose en el mismo. Suponiendo que la bala es una masa puntual, que el volante es un disco macizo y homogéneo (no se tiene en cuenta el pequeño diente). Calcular:
- La velocidad angular adquirida por el sistema disco - bala después del choque
- La energía perdida en el choque.
Este problema es de aplicación del principio de conservación del momento angular por que las fuerzas exteriores actúan en el eje del disco que permanece fijo, el disco solamente puede girar alrededor de su eje, no puede trasladarse. El momento de dichas fuerzas respecto del centro del disco es cero, por lo que el momento angular respecto del centro del disco es constante.
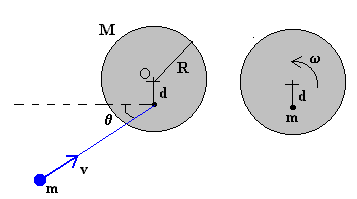
El momento angular inicial es el momento angular de la partícula respecto del eje del disco O.
Li=mdv·cosθ
El momento angular final, es el del disco con la partícula incrustada a una distancia d del centro del disco, girando con velocidad angular ω . El momento angular final es el producto del momento de inercia (del disco más la partícula) por la velocidad angular de rotación.
Aplicando el principio de conservación del momento angular, calculamos la velocidad angular ω de rotación del sistema formado por el disco y la partícula.
La energía perdida en la colisión es igual a la diferencia entre la energía final de rotación del sistema formado por el disco y la partícula, y la energía cinética de la partícula.
Completar una tabla como la siguiente y despejar la velocidad angular de rotación del disco.
| Masa de la bala m | |
| Velocidad de la bala v | |
| Angulo de disparo θ | |
| Distancia del blanco al eje del disco d | |
| Masa del disco M | |
| Radio del disco R | 50 cm |
| Velocidad angular de rotación ω |
|---|
Actividades
Se introduce
- La masa de la bala en gramos, en el control titulado Masa bala
- La velocidad de la bala en m/s, en el control titulado Velocidad
- La masa del disco en gramos, en el control titulado Masa disco
- El radio del disco está fijado en el programa interactivo en R=50 cm
- El ángulo de disparo se puede establecer en el control titulado Ángulo
- La distancia d entre el centro del disco y el punto de impacto, en el control titulado Distancia.
Se pulsa el botón titulado Nuevo.
Se muestra el balance energético de la colisión mediante un gráfico en la parte izquierda.
Considerar los siguientes casos:
- Cuando el ángulo de disparo es 0º
- Cuando el ángulo de disparo es 90º
- Cuando d es cero, el punto de impacto está en el centro del disco
- Cuando el punto de impacto está por encima del centro del disco y cuando está por debajo.

