Dos discos que se acoplan.

Conservación del momento angular

Tenemos un sistema formado por dos discos que giran alrededor de un eje común. El momento de las fuerzas exteriores respecto del eje de rotación O es nulo, por lo que se conserva el momento angular

$\vec{M_{e x t}} = \frac{d \vec{L}}{d t} \vec{M_{e x t}} = 0 \vec{L} = cte$

El momento angular de un sólido en rotación alrededor de un eje fijo con velocidad angular ω es $\vec{L} = I \vec{ω}$

La fórmula del momento de inercia I₀ de un disco respecto a un eje de rotación perpendicular al disco y que pase por su centro es $I_{0} = \frac{1}{2} m R^{2}$

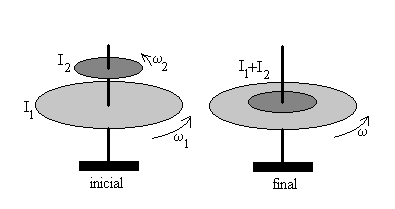
Momento angular antes del acoplamiento

El momento angular del sistema antes del acoplamiento es la suma de los momentos angulares de cada uno de los discos

L=I₁ω₁+ I₂ω₂

Donde ω₁y ω₂ son las velocidades angulares iniciales antes del acoplamiento.

Momento angular después del acoplamiento

Después del acoplamiento ambos discos llevan una velocidad angular común ω .

L=I₁ω + I₂ω

Principio de conservación del momento angular

Despejando la velocidad angular ω , tenemos

$ω = \frac{I_{1} ω_{1} + I_{2} ω_{2}}{I_{1} + I_{2}}$

Esta fórmula es similar al choque entre una bala y un bloque, cuando la bala se incrusta en el bloque.

Balance energético

Energía antes del acoplamiento

$E_{i} = \frac{1}{2} I_{1} ω_{1}^{2} + \frac{1}{2} I_{2} ω_{2}^{2}$

Energía después del acoplamiento

$E_{f} = \frac{1}{2} (I_{1} + I_{2}) ω^{2}$

El trabajo de la fuerza de rozamiento en el acoplamiento es W=E_f-E_i. Haciendo algunas simplificaciones llegamos a esta expresión final

$W = - \frac{1}{2} \frac{I_{1} I_{2}}{I_{1} + I_{2}} {(ω_{1} - ω_{2})}^{2}$

La energía final es siempre menor que la inicial E_f<E_i

El papel de las fuerza internas

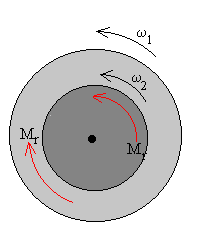
La velocidad angular de los discos acoplados cambia desde las velocidades angulares iniciales ω₁y ω₂ a la velocidad angular final ω a lo largo de un tiempo t.

Sobre los discos actúan fuerzas interiores de rozamiento entre las superficies en contacto de modo que, uno de los discos se acelera y el otro se decelera hasta que adquieren la misma velocidad angular final ω.

Estas fuerza interiores ejercen un momento M_r. Imaginemos que ω₁> ω₂, el momento M_r se opone a ω₁ decelerando el disco inferior y acelerando el disco superior tal como se muestra en la figura.

Imaginemos que ambos discos tienen momentos de inercia iguales I₁=I₂ y velocidades angulares iguales y de sentido contrario ω_{1 =}- ω₂, el momento M_r hace disminuir ambas velocidades, hasta que la velocidad angular final del conjunto es cero, tal como predice el principio de conservación del momento angular.

Ecuación de la dinámica de rotación

Formulamos la ecuación de la dinámica de rotación para cada uno de los discos

-M_r=I₁·α₁
M_r=I₂·α₂

Suponiendo que M_r es constante, las aceleraciones angulares son constantes, las velocidades angulares valdrán

ω₁ =ω₁₀+α₁t
ω₂=ω₂₀+α₂t

donde ω₁₀y ω₂₀ son las velocidades angulares iniciales en el instante t=0.

A partir de estas ecuaciones se puede calcular el tiempo t que tardan los discos en adquirir la misma velocidad angular ω₁=ω₂=ω.

$t = \frac{ω_{10} - ω_{20}}{α_{2} - α_{1}} = M_{r} \frac{I_{1} I_{2}}{I_{1} + I_{2}} (ω_{10} - ω_{20})$

Calculamos el desplazamiento de cada uno de los discos durante el intervalo de tiempo t.

$\begin{array}{l} θ_{1} = ω_{10} t + \frac{1}{2} α_{1} t^{2} \\ θ_{2} = ω_{20} t + \frac{1}{2} α_{2} t^{2} \end{array}$

Trabajo de las fuerzas internas

El trabajo del momento de la fuerza de rozamiento es

W=-M_r·θ₁+M_r·θ₂

Como vemos por las flechas en la figura, M_r es opuesto al desplazamiento θ₁ (trabajo negativo), y es del mismo sentido que el desplazamiento θ₂ (trabajo positivo).

Haciendo algunas operaciones llegamos en pocos pasos a la misma expresión para W que la que obtuvimos a partir del balance energético después de aplicar el principio de conservación del momento angular. Pero ahora, interpretamos mejor el origen de la disipación de la energía durante el tiempo t que dura el acoplamiento (hasta que los discos alcanzan la misma velocidad angular final).

$W = - \frac{1}{2} \frac{I_{1} I_{2}}{I_{1} + I_{2}} {(ω_{10} - ω_{20})}^{2}$

Medida del coeficiente cinético, μ_k

Se ha descrito los procedimientos de medida del coeficiente cinético μ_k en varias páginas páginas de este Curso

En este caso, mediremos el coeficiente cinético en un movimiento de rotación.

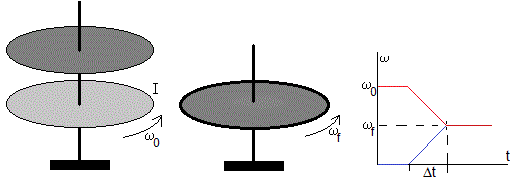
Un disco en reposo se deja caer sobre otro idéntico en rotación con velocidad angular ω₀. Cuando los dos discos entran en contacto, debido al momento M_r, los discos cambian de velocidad angular, el primero la incrementa y el segundo la disminuye hasta que alcanzan una velocidad angular común ω_f. La velocidad angular disminuye (aumenta) linealmente con el tiempo, la aceleración angular α es constante en el intervalo de tiempo Δt

En la página titulada, El rozamiento en el movimiento de rotación, obtuvimos una expresión para el momento de las fuerzas de rozamiento M_r

$M_{r} = \frac{2 μ M g R}{3}$

para un disco de masa M y radio R. Donde μ es coeficiente cinético

La ecuación de la dinámica de rotación aplicada a uno de los dos discos se escribe

$\begin{array}{l} I α = M_{r} \\ (\frac{1}{2} M R^{2}) α = \frac{2 μ M g R}{3} \\ μ = \frac{3 R}{4 g} α \end{array}$

Midiendo la aceleración angular α obtenemos el coeficiente cinético μ.

En una experiencia de laboratorio, se puede medir la velocidad angular de rotación con un sensor y comprobar que estas medidas, tomadas en el intervalo de tiempo Δt, se ajustan a una línea recta cuya pendiente α se puede obtener mediante el procedimiento de regresión lineal.

Por ejemplo, α=164 rad/s² y el radio del disco es R=4.45 cm. El coeficiente cinético es μ=0.558.

Ejemplos

Ejemplo 1º:

Momentos de inercia

Sea m₁=0.2 kg, r₁=1.0 m, I₁=0.1 kg·m²
Sea m₂=0.8 kg, r₂=0.5 m, I₂=0.1 kg·m²

Velocidades angulares iniciales

Sea ω₁=2 rad/s
Sea ω₂=0 rad/s

Principio de conservación del momento angular
0.1·2+0.1·0=(0.1+0.1)·ω , por lo que ω =1 rad/s

Balance energético
E_i=0.2 J
E_f=0.1 J
W=E_f-E_i=-0.1 J

Fuerzas internas

Sea el momento de las fuerza se rozamiento M_r=0.1 N·m. Calculamos las aceleraciones angulares de cada disco

-0.1=0.1·α₁
0.1=0.1·α₂

Ahora las velocidades angulares finales

ω₁=2-1·t
ω₂=0+1·t

Las velocidades angulares ω₁=ω₂ se hacen iguales en el instante t=1 s después de haberse acoplado. En este instante la velocidad angular común es 1 rad/s

Balance energético

Desplazamientos (ángulo girado por cada disco en el tiempo t)

θ₁=1.5 rad
θ₂=0.5 rad

Trabajo del momento de las fuerzas de rozamiento

W=-0.1·1.5+0.1·0.5=-0.1 J

El momento de las fuerzas de rozamiento se opone al desplazamiento del primer disco y favorece el del segundo

Obtenemos el mismo valor que en el apartado 1º

Ejemplo 2º

Un caso interesante se produce cuando ambos discos tienen el mismo momento de inercia, y velocidades angulares iguales y de sentido contrario

Momentos de inercia

Sea m₁=0.2 kg, r₁=1.0 m, I₁=0.1 kg·m²
Sea m₂=0.8 kg, r₂=0.5 m, I₂=0.1 kg·m²

Velocidades angulares iniciales

Sea ω₁=-4 rad/s
Sea ω₂=4 rad/s

Principio de conservación del momento angular

0.1·4-0.1·4=(0.1+0.1)·ω , por lo que ω=0 rad/s

Los discos se paran después de acoplarse

Balance energético

E_i=1.6 J
E_f=0.0 J

La pérdida de energía durante el acoplamiento

W=E_f-E_i=-1.6 J

Fuerzas internas

Sea el momento de las fuerza se rozamiento M_r=0.1 N·m. Calculamos las aceleraciones angulares de cada disco

-0.1=0.1·α₁
0.1=0.1·α₂

Ahora las velocidades angulares finales

ω₁=4-1·t
ω₂=-4+1·t

Las velocidades angulares ω₁=ω₂ se hacen iguales en el instante t=4 s después de haberse acoplado. En este instante la velocidad angular final común es cero

Balance energético

Desplazamientos (ángulo girado por los discos) durante el tiempo t

θ₁=8 rad
θ₂=-8 rad

Trabajo del momento de las fuerzas de rozamiento

W=-0.1·8+0.1·(-8)=-1.6 J

Fijarse ahora que el momento de las fuerzas de rozamiento se opone al desplazamiento de ambos discos

Actividades

Se introduce:

Masa del disco inferior m₁ (kg)
El radio del disco inferior está fijado en el programa r₁=1 m
Velocidad angular inicial ω₁ (rad/s)
Masa del disco superior m₂ (kg)
El radio del disco superior está fijado en el programa r₂=0.5 m
Velocidad angular inicial ω₂ (rad/s)
Momento de las fuerzas de rozamiento entre los discos M_r (N·m)

Se pulsa el botón titulado Nuevo y a continuación, ►.

Los discos empiezan a girar primero uno independientemente del otro. En la parte izquierda, tenemos un diagrama de dos barras, una para la energía y otra para el momento angular.

Se pulsa el botón titulado Acopla

Se activa un mecanismo que hace que el disco superior se acople con el inferior. Cuando están acoplados empieza a actuar el momento de las fuerzas de rozamiento.

En la parte derecha, observamos la evolución de la velocidad angular de cada disco en función del tiempo. Comprobamos que la magnitud del momento de la fuerza de rozamiento no afecta a la velocidad angular final común de ambos discos. Tan sólo, al tiempo que tardan en alcanzar dicho estado final.

Se muestra la energía y el momento angular de cada uno de los discos. La conservación del momento angular no implica la conservación de la energía. El efecto del acoplamiento es la disminución de la energía inicial que se pierde en forma de calor debido al rozamiento entre ambos discos, mientras que el momento angular permanece constante. El momento angular de un disco aumenta, el del otro disminuye pero la suma es constante.

Masa arriba(kg): V. angular(rad/s):
Masa abajo: V. angular:
Rozamiento(N·m):

Práctica de laboratorio

Fómulas de los momentos de inercia de los cuerpos utilizados en esta página, respecto de un eje que pasa por el centro de masas

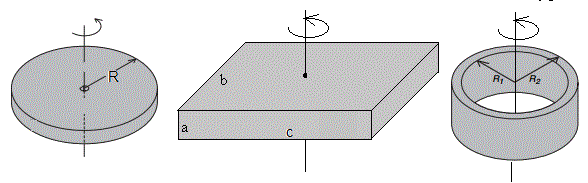
$I_{c} = \frac{1}{2} M R^{2} I_{c} = \frac{M}{12} (b^{2} + c^{2}) I_{C} = \frac{1}{2} m (R_{1}^{2} + R_{2}^{2})$

Experiencia 1

Disponemos de un disco de masa 1.422 kg y diámetro 23 cm, de momento de inercia I₁=1.422·0.115²/2=0.00940 kg m² que hacemos girar con velocidad angular ω₁=8.38 rad/s

Situamos encima un anillo de masa 1.418 kg, diámetro interior 10.7 cm y diámetro exterior 12.7 cm, de momento de inercia I₂=1.418·(0.0635²+0.0535²)/2=0.00489 kg m²

Aplicamos el principio de conservación del momento angular para calcular la velocidad angular final ω₂

$I_{1} ω_{1} = (I_{1} + I_{2}) ω_{2}$

El resultado es ω₂=5.51 rad/s. La medida efectuada en el laboratorio es de 5.22 rad/s

Experiencia 2

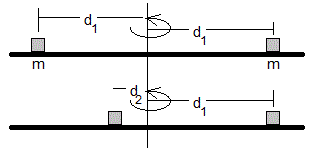
Sobre una barra soporte de momento de inercia I=0.0133 kgm² que hemos medido utilizando la dinámica de rotación, colocamos dos piezas prismáticas iguales de 4.4 cm de lado y 276 g de masa a una distancia d₁=20 cm del eje de rotación. El momento de inercia inicial es

$I_{1} = 0.0133 + 2 {\frac{0.276}{12} ({0.044}^{2} + {0.044}^{2}) + 0.276 \cdot {0.2}^{2}} = 0.0356 {kgm}^{2}$

Hacemos girar el soporte con las dos masas con una velocidad angular inicial ω₁=2.11 rad/s

Mediante una cuerda desplazamos una de las masas hacia el eje de rotación a una distancia de d₂=3 cm del eje de rotación, el momento de inercia final es

$\begin{array}{l} I_{2} = 0.0133 + {\frac{0.276}{12} ({0.044}^{2} + {0.044}^{2}) + 0.276 \cdot {0.2}^{2}} + \\ {\frac{0.276}{12} ({0.044}^{2} + {0.044}^{2}) + 0.276 \cdot {0.03}^{2}} = 0.0248 {kgm}^{2} \end{array}$

Al tirar de la cuerda estamos aplicando una fuerza que tiene dirección radial y por tanto su momento es nulo, el momento angular del sistema formado por el soporte y las dos masas se conserva

Al disminuir el momento de inercia la velocidad angular aumenta, de mod que se cumple I₁ω₁=I₂ω₂

Despejamos ω₂=3.03 rad/s. La medida efectuada en el laboratorio fué de ω₂=2.95 rad/s

Balance energético

Vamos a comprobar que el trabajo de la fuerza necesaria para desplazar hacia el eje la pieza rectangular es igual a la variación de la energía cinética de rotación

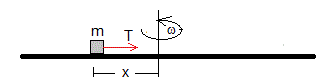
Cuando la pieza rectangular de masa m está a una distancia x del eje, la tensión T de la cuerda, es igual a la fuerza necesaria para que describa un movimiento circular de radio x con velocidad angular ω.

T=mω²x

Calculamos la velocidad angular de rotación ω mediante el principio de conservación del momento angular

I₁ω₁=I·ω

$\begin{array}{l} I_{1} = I_{0} + 2 (I_{b} + m d_{1}^{2}) = I_{0} + 2 I_{b} + 2 m d_{1}^{2} \\ I = I_{0} + (I_{b} + m d_{1}^{2}) + (I_{b} + m x^{2}) = I_{0} + 2 I_{b} + m d_{1}^{2} + m x^{2} = I_{1} - m d_{1}^{2} + m x^{2} \\ I_{2} = I_{0} + 2 I_{b} + m d_{1}^{2} + m d_{2}^{2} = I_{1} - m d_{1}^{2} + m d_{2}^{2} \end{array}$

I₀ es el momento de inercia del soporte, e I_b es el momento de inercia de la pieza rectangular

$\begin{array}{l} T = m {(\frac{I_{1} ω_{1}}{I_{1} - m d_{1}^{2} + m x^{2}})}^{2} x \\ W = \int_{d_{1}}^{d_{2}} T \cdot d x = \frac{I_{1}^{2} ω_{1}^{2}}{2} (\frac{1}{I_{2}} - \frac{1}{I_{1}}) = \frac{1}{2} \frac{I_{1}}{I_{2}} (I_{1} - I_{2}) ω_{1}^{2} \\ Δ E_{k} = \frac{1}{2} I_{2} ω_{2}^{2} - \frac{1}{2} I_{1} ω_{1}^{2} = \frac{1}{2} \frac{I_{1}}{I_{2}} (I_{1} - I_{2}) ω_{1}^{2} \end{array}$

Con los datos de esta experiencia, obtenemos ΔE_k=0.0345 J

Referencias

Robert Drosd, Leonid Minkin. Measuring the Coefficient of Kinetic Friction by Exploring Dynamics of Rotational Motion. The Physics Teacher, Vol. 58, March 2020, pp.176-178