En esta versión solamente es aplicable el principio de conservación del momento angular, ya que el sistema no es aislado sin embargo, el momento de las fuerzas exteriores respecto del eje de rotación O es nulo.

${\displaystyle \overrightarrow{M_{ext}}=\frac{d\overrightarrow{L}}{dt}\overrightarrow{M_{ext}}=0\overrightarrow{L}=\text{cte}}$

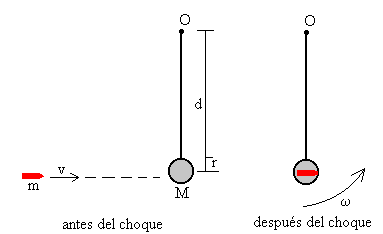
Principio de conservación del momento angular

• Momento angular antes del choque

Es el momento angular de la partícula respecto de O.

${\displaystyle \overrightarrow{L}=m\overrightarrow{r}\times \overrightarrow{v}}$

El módulo del momento angular es L=mv·d. Donde d es el brazo del momento angular o distancia entre la dirección de la velocidad y el punto O.

• Momento angular después del choque

Es el momento angular de un sólido rígido formado por la varilla, el cilindro y la bala empotrada, en rotación alrededor de un eje perpendicular al plano del dibujo que pasa por O.

${\displaystyle \overrightarrow{L}=I_0\overrightarrow{\omega }}$

El momento de inercia I₀ se compone de los siguientes términos:

• Se aplica el teorema de Steiner para obtener el momento de inercia del cilindro de masa M y radio r cuyo eje dista d de O
• Momento de inercia de una masa puntual m que dista d del eje de rotación
• La varilla tiene masa despreciable

${\displaystyle I_0=\left(\frac{1}{2}M{r}^2+M{d}^2\right)+m{d}^2}$

Como el momento angular inicial y final son iguales, despejamos la velocidad angular ω, justamente después del choque.

${\displaystyle \omega =\frac{mvd}{I_0}}$

El momento lineal del sistema no se conserva

El momento lineal inicial del sistema formado por la bala y el péndulo en reposo es

p_i=mv

El momento lineal final del sistema es

p_f=(m+M)v_f

Como la varilla no tiene masa y la bala impacta en el centro del cilindro, el centro de masa del sistema está en el centro del cilindro y_cm=d. La velocidad final del c.m. del sistema es

v_f=ω·d

Para otros casos no tan simples, se calcula el centro de masa del sistema y_cm. La velocidad final del c.m. sería v_f=ω·y_cm

${\displaystyle \Delta p=p_f-p_i=(m+M)\frac{mvd}{\frac{1}{2}M{r}^2+(M+m)d^2}d-mv}$

Si el radio r es cero, el cilindro se convierte en una masa puntual M, el momento lineal se conserva Δp=0. El principio de conservación del momento lineal y del momento angular dan los mismos resultados.

Fuerzas interiores y exteriores

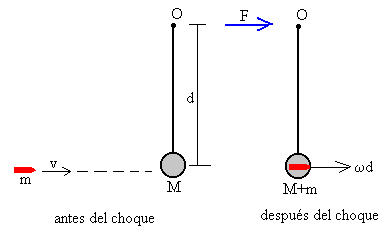
Una fuerza horizontal F actúa en el eje O del péndulo durante el tiempo Δt que dura el choque. El impulso de esta fuerza exterior F produce un cambio en el momento lineal del sistema. Si suponemos que F es constante durante este corto intervalo de tiempo,

F·Δt= Δp

El sentido de F será el indicado en la figura, si el momento lineal aumenta y el contrario, si disminuye.

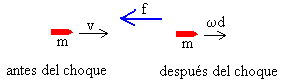
Durante el mismo tiempo Δt, la fuerza interna f que ejerce el cilindro sobre la bala, hace que ésta disminuya su velocidad de v a v_f=ω·d.

f·Δt= mωd-mv

Balance energético

• La energía antes del choque es la energía cinética de la bala $\frac{1}{2}m{v}^2$
• La energía después del choque es la energía cinética del sólido en rotación $\frac{1}{2}{I}_0{\omega }^2$

La energía perdida en la colisión es la diferencia entre estas dos energías. En la parte izquierda, observamos que la mayor parte de la energía cinética de la bala se convierte en energía de deformación cuando la bala se incrusta con el cilindro y solamente, una pequeña parte de la energía inicial se convierte en energía cinética de rotación del sistema formado por la varilla, el cilindro y la bala.

Movimiento después del choque

Dinámica de rotación

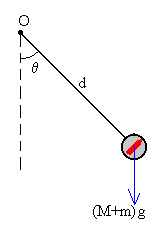
Después del choque tenemos un sólido rígido en rotación alrededor de un eje fijo que pasa por O.

La ecuación de la dinámica de rotación es M=I₀·α

M es el momento del peso que actúa en el centro de masa del sólido. Como la varilla tiene masa despreciable y la bala se aloja en el centro del cilindro, el centro de masa del sistema coincide con el centro del cilindro, a una distancia d del eje de rotación.

-(M+m)·g·d·sinθ =I₀·α

Como la aceleración angular no es constante, resolvemos la ecuación diferencial de segundo orden por procedimientos numéricos.

${\displaystyle \frac{d^2\theta }{d{t}^2}+\frac{(m+M)gd}{I_0}\sin \theta =0}$

con las condiciones iniciales siguientes: en el intante t=0, θ=0, dθ/dt=ω, velocidad angular después del choque.

Sin embargo, es mucho más fácil aplicar el principio de conservación de la energía para obtener información sobre el comportamiento del sólido en rotación.

Principio de conservación de la energía

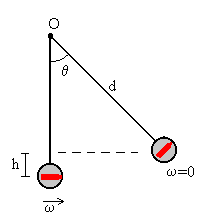
La energía cinética después del choque se convierte en energía potencial

${\displaystyle \frac{1}{2}{I}_0{\omega }^2=(M+m)ghh=d-d\cos \theta }$

Conocido el ángulo θ de máxima desviación del péndulo balístico, calculamos la velocidad de la bala antes del choque.

Puede ocurrir que la velocidad de la bala sea tan grande que el péndulo empiece a dar vueltas. Para que esto ocurra, la energía del péndulo después del choque tiene que ser mayor que la energía potencial del cilindro y de la bala correspondiente a una altura 2d.

${\displaystyle \frac{1}{2}{I}_0{\omega }^2\ge (M+m)g·2d}$

Mientras que una masa puntual en movimiento circular no puede tener una velocidad nula en el punto más alto de su trayectoria, un sólido rígido en rotación puede tener una velocidad angular nula. Esta es la diferencia esencial entre las dos versiones del péndulo balístico.

Ejemplos

• Masa de la bala m=0.2 kg
• Velocidad de la bala v=10 m/s
• Masa del cilindro M=1.5 kg
• Radio del cilindro r=3 cm=0.03 m
• Longitud de la varilla d=0.5 m

1. Choque. Principio de conservación del momento angular

Momento de inercia I₀= 0.426 kgm²

Momento angular inicial 0.2·10·0.5=1 kg·m²/s
Momento angular final I₀·ω

Conservación del momento angular ω =2.35 rad/s

2. Movimiento después del choque. Principio de conservación de la energía

La energía cinética después del choque se transforma en energía potencial, cuando se alcanza la máxima desviación del péndulo

${\displaystyle \frac{1}{2}1.7·{\left(2.35\right)}^2=1.7·9.8·hh=\text{0}\text{.07}\text{m}}$

Una vez calculado h se obtiene el ángulo de desviación θ=30.8º

Ejemplo 2º

Con estos datos, vamos a calcular la velocidad que deberá llevar la bala para que el péndulo se desplace 180º, se ponga en posición vertical.

1. Movimiento después del choque. Principio de conservación de la energía

La energía potencial de la bala y cilindro en dicha posición es 1.7·9.8·2·0.5=16.66 J

La energía cinética después del choque será $\frac{1}{2}{I}_0{\omega }^2=16.66\omega =8.85\text{rad/s}$

2. Choque. Principio de conservación del momento angular

0.2·v·0.5=I₀·ω

Despejando v=37.66 m/s

Introducimos este valor en el control titulado Velocidad bala y pulsamos el botón titulado Nuevo, observamos que el péndulo llega a la posición vertical sin sobrepasarla. Incrementamos en una centésima la velocidad de la bala v=37.67 m/s y vemos que el péndulo empieza a dar vueltas.

Actividades

Se introduce

• La masa m de la bala (kg), en el control titulado Masa de la bala
• La velocidad v de la bala (m/s), en el control titulado Velocidad bala
• Radio del cilindro (cm), en el control titulado Radio cilindro
• La masa del cilindro (kg), en el control titulado Masa
• La longitud de la varilla está fijada por el programa 0.5 m

Se pulsa el botón Nuevo

Se observa sobre la escala angular graduada el máximo desplazamiento del péndulo. Su valor numérico se muestra en la esquina superior izquierda. También podemos ver a la izquierda, un gráfico que muestra el balance energético de la colisión.

Fuerzas sobre la barra en en eje de rotación

Si la varilla tiene masa despreciable, el centro de masas se encuentra en el centro del cilindro de masa M y radio r, donde también se encuentra alojada la bala de masa m.

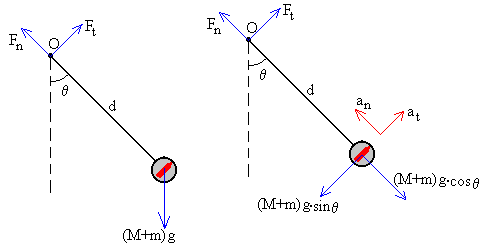
En la figura de la izquierda, se muestra las fuerzas sobre el conjunto formado por la barra, el cilindro y la bala. En la figura de la derecha, la descomposición de dichas fuerzas según los ejes que se indican.

Hemos calculado la aceleración angular y la velocidad angular del sistema después del choque cuando la barra forma un ángulo θ con la vertical tal como se ve en la figura.

• Ecuación de la dinámica de rotación

I₀α =-(M+m)g·d·sinθ

• Balance energético

${\displaystyle \frac{1}{2}{I}_0{\omega }_0^2=(M+m)g·d(1-\cos \theta )+\frac{1}{2}{I}_0{\omega }^2}$

Siendo ω₀ la velocidad angular del sólido inmediatamente después del choque

El centro de masas describe un arco de circunferencia de radio d, por tanto, tiene dos aceleraciones, una tangencial a_t y otra normal a_n.

En la figura de la izquierda, se han dibujado las fuerzas sobre el sistema. A la derecha, se ha sustituido el peso por sus componentes y se han dibujado las componentes tangencial y normal de la aceleración. A partir de este esquema, planteamos las ecuaciones del movimiento del centro de masas.

(M+m)·a_t=F_t-(M+m)g·sinθ
(M+m)·a_n=F_n-(M+m)g·cosθ

Teniendo en cuenta que en un movimiento circular

a_t=α ·d
a_n=ω ²·d

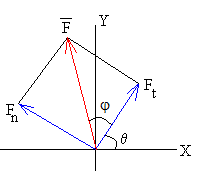
Despejamos F_t y F_n

F_t =(M+m)·α ·d +(M+m)g·sinθ
F_n =(M+m)·ω ²·d +(M+m)g·cosθ

La fuerza $\overrightarrow{F}$ sobre la barra en el eje de rotación es

${\displaystyle \begin{array}{l}F=\sqrt{F_t^2+F_n^2}\\ \phi =\theta +\arctan \frac{F_n}{F_t}\end{array}}$

Ejemplo

Volvemos al ejemplo 1º

• Masa de la bala m=0.2 kg
• Velocidad de la bala v=10 m/s
• Masa del cilindro M=1.5 kg
• Radio del cilindro r=3 cm=0.03 m
• La longitud de la varilla d=0.5 m

Momento de inercia I₀= 0.426 kgm²

1. Choque. Aplicando el principio de conservación del momento angular obtuvimos la velocidad angular del sistema después del choque

ω₀=2.35 rad/s

El problema va a consistir ahora en calcular las fuerzas F_t y F_n en el eje O, cuando el ángulo θ =15º.

2. Calculamos la aceleración angular α y la velocidad angular ω.

0.426α =-1.7·9.8·0.5 sin15º,    α =-5.06 rad/s²

3. Balance energético

${\displaystyle \frac{1}{2}0.426·{2.35}^2=1.7·9.8·0.5(1-\cos 15º)+\frac{1}{2}\text{0}\text{.426·}{\omega }^{\text{2}}\omega =2.04\text{rad/s}}$

4. Calculamos las componentes F_t y F_n de la fuerza en el eje O.

F_t=(M+m)g·sinθ +(M+m)a_t= 1.7·9.8·sin15º-1.7·0.5·5.06=0.007 N
F_n (M+m)g·cosθ +(M+m)·a_n =1.7·9.8·cos15º+1.7·0.5·2.04²=19.65 N

5. La fuerza sobre la barra en el eje de rotación

Módulo F=19.65 N
Ángulo que forma con el eje X, φ=105º