Medida del módulo de elasticidad
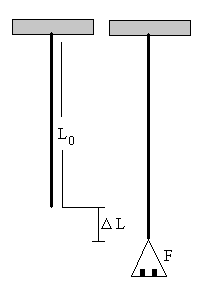
Un hilo metálico sometido a un esfuerzo de tracción sufre una deformación que consiste en el aumento de longitud y en una contracción de su sección.
Supondremos que el aumento de longitud es el efecto dominante, sobre todo en hilos largos y de pequeña sección. Estudiaremos el comportamiento elástico de los hilos, aquél en el que existe una relación de proporcionalidad entre la fuerza F aplicada al hilo y el incremento ΔL de su longitud o bien, entre el esfuerzo F/S y la deformación unitaria ΔL/L0.
Donde S es la sección del hilo S=π r2, y Y es una constante de proporcionalidad característica de cada material que se denomina módulo de elasticidad o módulo de Young.
| Metal | Módulo de Young, Y·1010 N/m2 |
|---|---|
| Cobre estirado en frío | 12.7 |
| Cobre, fundición | 8.2 |
| Cobre laminado | 10.8 |
| Aluminio | 6.3-7.0 |
| Acero al carbono | 19.5-20.5 |
| Acero aleado | 20.6 |
| Acero, fundición | 17.0 |
| Cinc laminado | 8.2 |
| Latón estirado en frío | 8.9-9.7 |
| Latón naval laminado | 9.8 |
| Bronce de aluminio | 10.3 |
| Titanio | 11.6 |
| Níquel | 20.4 |
| Plata | 8.27 |
Fuente: Koshkin N. I., Shirkévich M. G.. Manual de Física Elemental. Editorial Mir 1975.

Representando el esfuerzo en función de la deformación unitaria para un metal obtenemos una curva característica semejante a la que se muestra en la figura.
Durante la primera parte de la curva, el esfuerzo es proporcional a la deformación unitaria, estamos en la región elástica. Cuando se disminuye el esfuerzo, el material vuelve a su longitud inicial. La línea recta termina en un punto denominado límite elástico.
Si se sigue aumentando el esfuerzo la deformación unitaria aumenta rápidamente, pero al reducir el esfuerzo, el material no recobra su longitud inicial. La longitud que corresponde a un esfuerzo nulo es ahora mayor que la inicial L0, y se dice que el material ha adquirido una deformación permanente.
El material se deforma hasta un máximo, denominado punto de ruptura. Entre el límite de la deformación elástica y el punto de ruptura tiene lugar la deformación plástica.
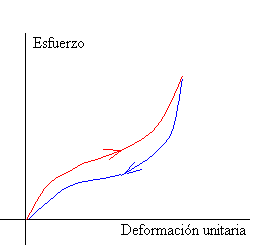
Si entre el límite de la región elástica y el punto de ruptura tiene lugar una gran deformación plástica el material se denomina dúctil. Sin embargo, si la ruptura ocurre poco después del límite elástico el material se denomina frágil.
En la figura, se representa el comportamiento típico de esfuerzo - deformación unitaria de un material como el caucho. El esfuerzo no es proporcional a la deformación unitaria (curva de color rojo), sin embargo, la sustancia es elástica en el sentido que si se suprime la fuerza sobre el material, el caucho recupera su longitud inicial. Al disminuir el esfuerzo la curva de retorno (en color azul) no es recorrida en sentido contrario.
La falta de coincidencia de las curvas de incremento y disminución del esfuerzo se denomina histéresis elástica. Un comportamiento análogo se encuentra en las sustancias magnéticas.
Puede demostrarse que el área encerrada por ambas curvas es proporcional a la energía disipada en el interior del material elástico. La gran histéresis elástica de algunas gomas las hace especialmente apropiadas para absorber las vibraciones.
Medida del módulo de elasticidad
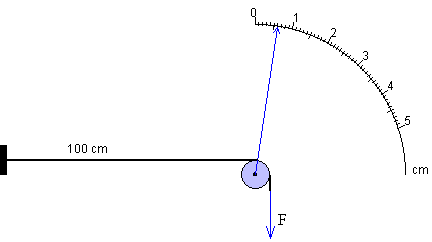
En la figura, se muestra el dispositivo experimental. Se emplea un hilo de un metro de longitud dispuesto horizontalmente fijado por un extremo, mientras que el otro pasa por una polea. Del extremo libre se cuelgan pesas de 100 g, 250 g ó 500 g.
Al poner pesas sobre el extremo libre del hilo, el alambre se alarga y la polea gira un ángulo igual a ΔL/r. Siendo r el radio de la polea.
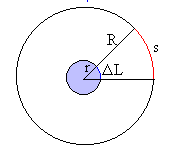
Como el alargamiento ΔL es pequeño, se puede medir mediante una aguja indicadora que marca sobre un sector circular cuyo radio es R=10·r veces el radio de la polea.
Como vemos en la figura, las longitudes de los arcos son proporcionales a los radios, de modo que
El arco s es 10 veces mayor que el alargamiento ΔL.
Ejemplo:
- Radio de la sección del hilo, 0.25 mm
- Material, Aluminio
- Se colocamos 6 pesas de 250 g en el extremo libre del hilo
La fuerza aplicada es F=mg=6·0.25·9.8 N
La lectura en la escala graduada semicircular es s=1.19 cm, que corresponde a una deformación de ΔL=1.19 mm.
El cociente entre el esfuerzo y la deformación es el módulo de Young
Y=6.29·1010 N/m2
Representación gráfica de los datos "experimentales"
- En el eje vertical la deformación ΔL, en m
- En el eje horizontal se representa el peso m en kg.
Se calcula y representa la recta que mejor ajusta a los datos experimentales por el procedimiento de la regresión lineal.
>> m=[250,500,750,1000,1250,1500,1750]/1000; %kg
>> dL=[0.20,0.40,0.59,0.79,0.99,1.19,1.39]/1000; %m
>> plot(m,dL,'ro','markersize',4,'markerfacecolor','r')
>> xlabel('m (kg)')
>> ylabel('\DeltaL (m)')
>> title('Módulo de Young')
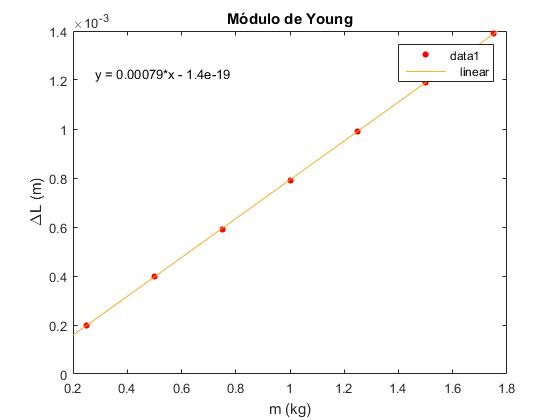
En el menú seleccionamos Tools/Basic Fitting, aparece un cuadro de diálogo donde marcamos la casilla linear en Plot fits. A continuación, pulsamos la flecha hacia la derecha --> para mostrar los coeficientes p1 y p2 del polinomio (recta) y=p1*x+p2 de ajuste.
Sea a=ΔL/m la pendiente de la recta en m/kg. El módulo de Young se calcula a partir del valor de la pendiente a
Supongamos que se ha realizado la "experiencia" con un hilo
- El radio de la sección del hilo, r=0.25 mm
- El material, Aluminio
La pendiente de la recta a= 7.9286·10-4 m/kg. El módulo de Young es, entonces
Actividades
Se introduce
- El radio del hilo en mm, en el control titulado Radio
- El metal del que está hecho el hilo, en el control titulado Material
- El tipo de pesa que cuelga del extremo libre del hilo, activando el botón de radio titulado Pesas (g): 100, 250, 500.
Se pulsa el botón titulado Nuevo
Se arrastra con el puntero del ratón la pesa que aparece en la parte inferior derecha y se engancha en el extremo del hilo, o en la parte inferior de una pesa previamente colocada.

