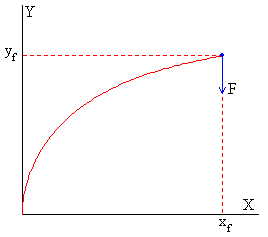
Supondremos que

• El material del que está hecha la barra es elástico, lineal, homogéneo e isótropo, que la relación entre la tensión y la deformación viene dada por la ley de Hooke.

• La longitud L, es mucho mayor que las dimensiones de su sección trasversal, y que la deformación debida a su propio peso es despreciable.

Que en estas condiciones es aplicable la ecuación de Euler-Bernoulli que relaciona el momento flector M de la fuerza aplicada y el radio de curvatura ρ de la barra deformada

${\displaystyle M=\frac{Y·I}{\rho }}$

donde Y es el módulo de Young del material e I es el momento de inercia de la sección trasversal respecto del eje neutro.

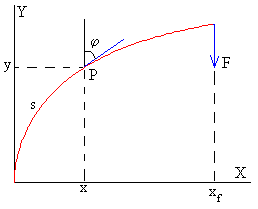
El radio de curvatura ρ=ds/dφ

${\displaystyle \frac{d\phi }{ds}=\frac{M}{Y·I}}$

El momento flector M de la fuerza F aplicada en el extremo libre de la barra respecto del punto P (x, y) es

${\displaystyle \begin{array}{l}M=F(x_f-x)\\ \frac{d\phi }{ds}=\frac{F}{Y·I}(x_f-x)\end{array}}$

Derivando con respecto a s, y teniendo en cuenta que sinφ=dx/ds

${\displaystyle \frac{d^2\phi }{d{s}^2}+\frac{F}{Y·I}\text{sin}\phi =0}$

que es una ecuación diferencial similar a la que describe el movimiento de un péndulo. Para determinar φ(s) se resuelve la ecuación diferencial con las siguientes condiciones iniciales:

${\displaystyle \phi (0)=0{\frac{d\phi }{ds}|}_{s=L}=0}$

ya que en el extremo libre de la barra x=x_f ó s=L, el momento M es cero y por tanto dφ/ds=0

Se trata de condiciones iniciales que se evalúan en distintos puntos s=0, y s=L. Por ejemplo, para un péndulo que se suelta cuando se desvía un ángulo θ₀ de la posición de equilibrio, las condiciones iniciales son t=0, θ=θ₀, dθ/dt=0 que se evalúan ambas en el instante inicial.

En la siguiente tabla, establecemos analogías entre las magnitudes que describen el movimiento de un péndulo simple y el y pandeo de una barra empotrada en un extremo

Para obtener una solución de la ecuación diferencial, multiplicamos por dφ/ds la ecuación diferencial

${\displaystyle \begin{array}{l}\frac{d\phi }{ds}\frac{d^2\phi }{d{s}^2}+\frac{F}{Y·I}\frac{d\phi }{ds}\text{sin}\phi =0\\ \frac{d}{ds}\left(\frac{1}{2}{\left(\frac{d\phi }{ds}\right)}^2-\frac{F}{Y·I}\text{cos}\phi \right)=0\\ \frac{1}{2}{\left(\frac{d\phi }{ds}\right)}^2-\frac{F}{Y·I}\text{cos}\phi =\text{cte}\end{array}}$

Determinamos la constante de integración sabiendo que φ(L)= φ_0, donde φ₀ es la pendiente desconocida en el extremo libre de la barra y que dφ/ds=0 para s=L.

${\displaystyle \begin{array}{l}{\left(\frac{d\phi }{ds}\right)}^2=\frac{2F}{Y·I}\left(\text{cos}\phi -\text{cos}{\phi }_0\right)\\ ds=\sqrt{\frac{Y·I}{2F}}\frac{d\phi }{\sqrt{\text{cos}\phi -\text{cos}{\phi }_0}}\end{array}}$

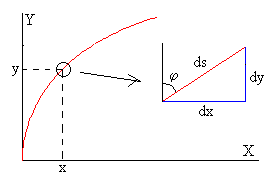
La Longitud L de la barra y las coordenadas x e y de cada uno de los puntos de la misma se obtienen

$$\begin{gathered} {\displaystyle \begin{array}{l}L={\displaystyle \underset{0}{\overset{{\phi }_0}{\int }}ds}L=\sqrt{\frac{Y·I}{2F}}{\displaystyle \underset{0}{\overset{{\phi }_0}{\int }}\frac{d\phi }{\sqrt{\text{cos}\phi -\text{cos}{\phi }_0}}}\\ dx=ds·\text{sin}\phi x=\sqrt{\frac{Y·I}{2F}}{\displaystyle \underset{0}{\overset{\phi }{\int }}\frac{\text{sin}\phi ·d\phi }{\sqrt{\text{cos}\phi -\cos {\phi }_0}}}= \\ \sqrt{\frac{2Y·I}{F}}\left(\sqrt{\text{1-cos}{\phi }_0}-\sqrt{\text{cos}\phi -\text{cos}{\phi }_0}\right)\\ dy=ds·\text{cos}\phi y=\sqrt{\frac{Y·I}{2F}}{\displaystyle \underset{0}{\overset{\phi }{\int }}\frac{\text{cos}\phi ·d\phi }{\sqrt{\text{cos}\phi -\cos {\phi }_0}}}\end{array}} \end{gathered}$$

Dada la fuerza F aplicada en el extremo libre de la barra y conocida la longitud L de la barra, se resuelve la primera ecuación para calcular el ángulo φ₀, que forma la recta tangente a la barra en su extremo libre con el eje vertical Y

Una vez que se conoce este ángulo φ₀, se calcula la abscisa x dando valores al ángulo φ en el intervalo (0, φ₀)

El cálculo de la ordenada y es más complicado, ya que para cada valor del ángulo φ hay que hallar una integral definida en el intervalo (0, φ) empleando procedimientos numéricos.

Expresamos las ecuaciones anteriores de forma alternativa

${\displaystyle \begin{array}{l}2\sqrt{\alpha }={\displaystyle \underset{0}{\overset{{\phi }_0}{\int }}\frac{d\phi }{\sqrt{\text{cos}\phi -\text{cos}{\phi }_0}}}\alpha =\frac{F{L}^2}{2Y·I}\\ \frac{x}{L}=\frac{1}{\sqrt{\alpha }}\left(\sqrt{\text{1-cos}{\phi }_0}-\sqrt{\text{cos}\phi -\cos {\phi }_0}\right)\\ \frac{y}{L}=\frac{1}{2\sqrt{\alpha }}{\displaystyle \underset{0}{\overset{\phi }{\int }}\frac{\text{cos}\phi ·d\phi }{\sqrt{\text{cos}\phi -\text{cos}{\phi }_0}}}\end{array}}$

Donde α es un parámetro adimensional que engloba las características geométricas de la barra, del material del que está hecha, y de la fuerza aplicada en su extremo libre

La primera integral se puede reducir a una integral elíptica de primera especie,

${\displaystyle {\displaystyle \underset{0}{\overset{{\phi }_0}{\int }}\frac{d\phi }{\sqrt{\text{cos}\phi -\text{cos}{\phi }_0}}}=\frac{1}{\sqrt{2}}{\displaystyle \underset{0}{\overset{{\phi }_0}{\int }}\frac{d\phi }{\sqrt{{\text{sin}}^2\frac{{\phi }_0}{2}-{\text{sin}}^2\frac{\phi }{2}}}}}$

se hace a continuación el cambio de variable

${\displaystyle \begin{array}{l}\text{sin}\phi =\frac{\text{sin}\left(\phi /2\right)}{k}k=\text{sin}\frac{{\phi }_0}{2}\\ d\phi =\frac{2k\cos \phi ·d\phi }{\sqrt{1-k^2{\text{sin}}^2\phi }}\\ {\displaystyle \underset{0}{\overset{{\phi }_0}{\int }}\frac{d\phi }{\sqrt{\text{cos}\phi -\text{cos}{\phi }_0}}}=\sqrt{2}{\displaystyle \underset{0}{\overset{\pi /2}{\int }}\frac{d\phi }{\sqrt{1-k^2{\text{sin}}^2\phi }}}\end{array}}$

Procedimiento numérico

Cálculo de φ₀.

Empezamos con la primera ecuación que nos determina el ángulo φ₀ que forma la recta tangente a la barra en su extremo libre con la dirección vertical , tal como se ve en la figura

${\displaystyle \sqrt{2\alpha }={\displaystyle \underset{0}{\overset{\pi /2}{\int }}\frac{d\phi }{\sqrt{1-k^2{\text{sin}}^2\phi }}}k=\text{sin}\frac{{\phi }_{\text{0}}}{\text{2}}}$

El programa interactivo al final de esta página, calcula la integral elíptica de primera especie E(k, π/2) mediante el procedimiento de Carlson. Véase Numerical Recipes in C, Special functions. Capítulo 6º. La raíz de la ecuación se obtiene por el procedimiento del punto medio.

Cálculo de las coordenadas (x/L, y/L) de cada punto de la barra deformada

El cálculo de x/L no reviste dificultad alguna. Conocido φ₀, se calcula x/L para cada ángulo φ en el intervalo (0, φ₀).

${\displaystyle \frac{x}{L}=\frac{1}{\sqrt{\alpha }}\left(\sqrt{\text{1-cos}{\phi }_0}-\sqrt{\text{cos}\phi -\cos {\phi }_0}\right)}$

El cálculo de y/L es más problemático. Conocido φ₀, se determina la ordenada y/L para cada ángulo φ en el intervalo (0,  φ₀)  calculando la integral definida,

${\displaystyle \frac{y}{L}=\frac{1}{2\sqrt{\alpha }}{\displaystyle \underset{0}{\overset{\phi }{\int }}\frac{\text{cos}\phi ·d\phi }{\sqrt{\text{cos}\phi -\text{cos}{\phi }_0}}}}$

por procedimientos numéricos

alfa=1.9*pi^2/8;
f=@(x) sqrt(2*alfa)-ellipke(sin(x/2)^2);
angFinal=fzero(f,[0,3]);
delta=angFinal/100;
xp=zeros(0,101);
yp=zeros(0,101);
xp(1)=0;
yp(1)=0;
i=1;
f=@(x) cos(x)./sqrt(cos(x)-cos(angFinal));
for ang=delta:delta:angFinal;
    i=i+1;
    xp(i)=(sqrt(1-cos(angFinal))-sqrt(cos(ang)-cos(angFinal)))/sqrt(alfa);
    yp(i)=integral(f,0, ang)/(2*sqrt(alfa));
end
plot(xp,yp)
axis equal
xlim([0 0.85])
grid on
xlabel('x')
ylabel('y')
title('Pandeo de una barra')

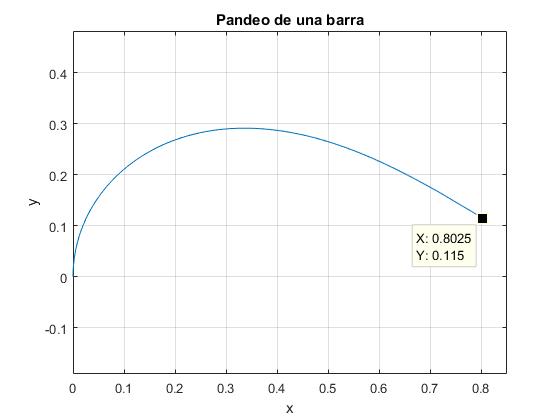
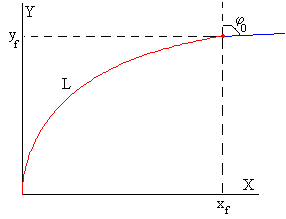
Cuando φ→φ₀ el denominador de la integral tiende a cero. El ordenador no calcula correctamente la ordenada y_f/L del extremo libre de la barra cuando φ=φ₀. Para solucionar este inconveniente, empleamos el procedimiento de interpolación que se muestra en la figura.

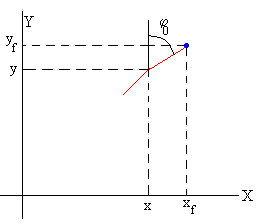
• Calculamos las coordenadas (x/L, y/L) para el ángulo φ=φ₀-Δφ, siendo Δφ un ángulo pequeño

• Calculamos la abscisa x_f/L para el ángulo φ₀

${\displaystyle \frac{x_f}{L}=\sqrt{\frac{\text{1-cos}{\phi }_0}{\alpha }}}$

• La ordenada y_f/L se obtiene resolviendo el triángulo rectángulo de la figura

${\displaystyle y_f=y+\frac{x_f-x}{\tan {\phi }_0}}$

Si ocurriera este caso, el script se modificaría en la representación gráfica.

%....
for ang=delta:delta:angFinal-delta;
    i=i+1;
    xp(i)=(sqrt(1-cos(angFinal))-sqrt(cos(ang)-cos(angFinal)))/sqrt(alfa);
    yp(i)=integral(f,0, ang)/(2*sqrt(alfa));
end
xf=sqrt((1.0-cos(angFinal))/alfa);
yp(i+1)=yp(i)+(xf-xp(i))/tan(angFinal);
xp(i+1)=xf;
%....

Aproximación de pequeñas flexiones

Cuando el ángulo φ y φ₀ son pequeños

${\displaystyle \cos \phi \approx 1-\frac{{\phi }^2}{2}\cos {\phi }_0\approx 1-\frac{{\phi }_0^2}{2}}$

La ecuación que calcula el ángulo φ₀ que forma la tangente a la barra en el extremo libre

${\displaystyle 2\sqrt{\alpha }={\displaystyle \underset{0}{\overset{{\phi }_0}{\int }}\frac{d\phi }{\sqrt{\text{cos}\phi -\text{cos}{\phi }_0}}}\alpha =\frac{F{L}^2}{2Y·I}}$

se convierte en

${\displaystyle \begin{array}{l}2\sqrt{\alpha }=\sqrt{2}{\displaystyle \underset{0}{\overset{{\phi }_0}{\int }}\frac{d\phi }{\sqrt{{\phi }_0^2-{\phi }^2}}}\\ 2\sqrt{\alpha }=\sqrt{2}\frac{\pi }{2}{F}_0=\frac{{\pi }^{2}Y·I}{4L^2}\end{array}}$

La integral se resuelve de forma inmediata haciendo el cambio de variable φ=φ₀·sint

Curiosamente, desaparece el ángulo φ₀ de la integral, esto implica que el ángulo φ₀ no depende de la fuerza aplicada F en el extremo de la barra para pequeñas flexiones.

Examinaremos el comportamiento de la barra elástica en función del parámetro adimensional

${\displaystyle \frac{F}{F_0}=\frac{8}{{\pi }^2}\alpha }$

Cuando F/F₀≤1 la barra no se desvía de su posición de equilibrio inicial.

Cuando F/F₀>1 la barra flexiona y su extremo libre se desvía:

• horizontalmente x_f,

• verticalmente 1-y_f de la posición inicial de equilibrio.

Actividades

Se introduce

• El cociente F/F₀≥1 en el control titulado Fuerza

Se pulsa el botón titulado Nuevo

Se representa una barra de longitud L=1 m deformada por la fuerza F aplicada en su extremo libre. Se proporcionan los datos de las coordenadas (x_f, y_f) de dicho punto y el ángulo φ₀, que forma la recta tangente a la barra en su extremo libre con el eje vertical Y

Se sugiere al lector, representar tres gráficas, en el eje X, el cociente F/F₀, y en eje Y

1. El ángulo φ₀, que forma la recta tangente a la barra en su extremo libre con el eje vertical

2. La desviación a lo largo del eje X del extremo libre δ_x=x_f

3. La desviación a lo largo del eje Y del extremo libre δ_y=1.0-y_f 

Ejemplo:

Sea una regla de acero de longitud L=30 cm, sección rectangular a=3.04 cm, y b=0.078 cm. El módulo de Young es Y=2.06·10¹¹ N/m²

El momento de inercia I vale

${\displaystyle I=\frac{a{b}^3}{12}=1.20·{10}^{-12}{\text{m}}^{\text{4}}}$

La fuerza critica es F₀=6.79 N

Cuando aplicamos en el extremo libre de la barra una fuerza tal que F/F₀=1.5, es decir F=10.18 N, observamos que se encuentra en x_f/L=0.79 e y_f/L=0.36.

Referencias

Beléndez T., Neipp C., Beléndez A., An integrated project for teaching the post-buckling of a slender cantilever bar. International Journal of Mechanical Engineering Education Vol. 32, nº 1, (2004) pp. 78-92.

Beléndez T., Neipp C., Beléndez A., Pandeo de una barra delgada empotrada en un extremo: Análisis lineal de un problema no lineal. Revista Española de Física 18 (3) Julio-Septiembre 2004, págs. 41-46.