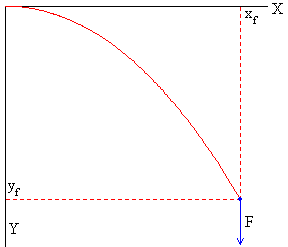
Consideremos una barra delgada de longitud L en posición horizontal, empotrada por un extremo y sometida a una fuera vertical F en el extremo libre. Determinaremos la forma de la barra y las coordenadas (x_f, y_f) del extremo libre para grandes flexiones de la barra.

Supondremos que

• La barra tiene una longitud L mucho mayor que las dimensiones de su sección trasversal y que la deformación debida a su propio peso es despreciable.

• Que la sección de la barra no cambia cuando se dobla. Cuando el espesor de la barra es pequeño comparado con el radio de curvatura, la sección trasversal cambia muy poco.

Que en estas condiciones es aplicable la ecuación de Euler-Bernoulli que relaciona el momento flector M de la fuerza aplicada y el radio de curvatura ρ de la barra deformada

${\displaystyle M=\frac{Y·I}{\rho }}$

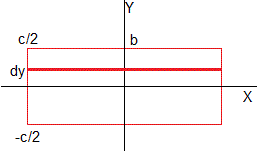
donde Y es el módulo de Young del material e I es el momento de inercia de la sección trasversal respecto del eje neutro.

${\displaystyle I={\displaystyle \int y^{2}dA={\displaystyle \underset{-c/2}{\overset{c/2}{\int }}{y}^2\left(b·dy\right)}}=\frac{b{c}^3}{12}}$

El radio de curvatura ρ=ds/dφ

${\displaystyle \frac{d\phi }{ds}=\frac{M}{Y·I}}$

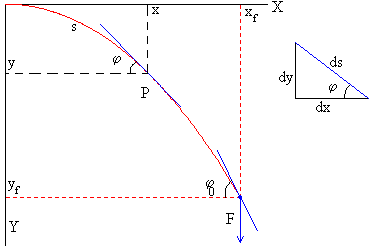
El momento flector M de la fuerza F aplicada en el extremo libre de la barra respecto del punto P (x, y) es M=F(x_f-x)

${\displaystyle \frac{d\phi }{ds}=\frac{F}{Y·I}(x_f-x)}$

Derivando con respecto a s, y teniendo en cuanta que cosφ=dx/ds

${\displaystyle \frac{d^2\phi }{d{s}^2}+\frac{F}{Y·I}\text{cos}\phi =0}$

Para determinar φ(s) se resuelve la ecuación diferencial con las siguientes condiciones iniciales:

${\displaystyle \phi (L)={\phi }_0{\frac{d\phi }{ds}|}_{s=L}=0}$

Para obtener una solución de la ecuación diferencial, multiplicamos por dφ/ds la ecuación diferencial

${\displaystyle \begin{array}{l}\frac{d\phi }{ds}\frac{d^2\phi }{d{s}^2}+\frac{F}{Y·I}\frac{d\phi }{ds}\text{cos}\phi =0\\ \frac{d}{ds}\left(\frac{1}{2}{\left(\frac{d\phi }{ds}\right)}^2+\frac{F}{Y·I}\sin \phi \right)=0\\ \frac{1}{2}{\left(\frac{d\phi }{ds}\right)}^2+\frac{F}{Y·I}\sin \phi =\text{cte}\end{array}}$

Determinamos la constante de integración a partir de las condiciones iniciales especificadas anteriormente

${\displaystyle \begin{array}{l}{\left(\frac{d\phi }{ds}\right)}^2=\frac{2F}{Y·I}\left(\sin {\phi }_0-\sin \phi \right)\\ ds=\sqrt{\frac{Y·I}{2F}}\frac{d\phi }{\sqrt{\sin {\phi }_0-\sin \phi }}\end{array}}$

La Longitud L de la barra y las coordenadas x e y de cada uno de los puntos de la misma se obtienen

$$\begin{gathered} {\displaystyle \begin{array}{l}L={\displaystyle \underset{0}{\overset{{\phi }_0}{\int }}ds}L=\sqrt{\frac{Y·I}{2F}}{\displaystyle \underset{0}{\overset{{\phi }_0}{\int }}\frac{d\phi }{\sqrt{\sin {\phi }_0-\sin \phi }}}\\ dx=ds·\cos \phi x=\sqrt{\frac{Y·I}{2F}}{\displaystyle \underset{0}{\overset{\phi }{\int }}\frac{\cos \phi ·d\phi }{\sqrt{\sin {\phi }_0-\sin \phi }}}= \\ \sqrt{\frac{2Y·I}{F}}\left(\sqrt{\sin {\phi }_0}-\sqrt{\sin {\phi }_0-\sin \phi }\right)\\ dy=ds·\sin \phi y=\sqrt{\frac{Y·I}{2F}}{\displaystyle \underset{0}{\overset{\phi }{\int }}\frac{\sin \phi ·d\phi }{\sqrt{\sin {\phi }_0-\sin \phi }}}\end{array}} \end{gathered}$$

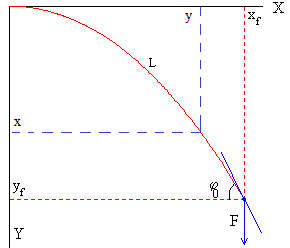
Dada la fuerza F aplicada en el extremo libre de la barra y conocida la longitud L de la barra, se resuelve la primera ecuación para calcular el ángulo φ₀, que forma la recta tangente a la barra en su extremo libre con la parte negativa del eje horizontal X

Una vez que se conoce este ángulo φ₀, se calcula la abscisa x dando valores al ángulo φ en el intervalo (0, φ₀)

El cálculo de la ordenada y es más complicado, ya que para cada valor del ángulo φ hay que hallar una integral definida en el intervalo (0, φ) empleando procedimientos numéricos.

Expresamos las ecuaciones anteriores de forma alternativa

${\displaystyle \begin{array}{l}2\sqrt{\alpha }={\displaystyle \underset{0}{\overset{{\phi }_0}{\int }}\frac{d\phi }{\sqrt{\sin {\phi }_0-\sin \phi }}}\alpha =\frac{F{L}^2}{2Y·I}\\ \frac{x}{L}=\frac{1}{\sqrt{\alpha }}\left(\sqrt{\sin {\phi }_0}-\sqrt{\sin {\phi }_0-\sin \phi }\right)\\ \frac{y}{L}=\frac{1}{2\sqrt{\alpha }}{\displaystyle \underset{0}{\overset{\phi }{\int }}\frac{\sin \phi ·d\phi }{\sqrt{\sin {\phi }_0-\sin \phi }}}\end{array}}$

Donde α es un parámetro adimensional que engloba las características geométricas de la barra, del material del que está hecha, y de la fuerza aplicada en su extremo libre

La primera integral se puede expresar en términos de la suma de dos integrales elípticas de primera especie, partiendo de la identidad trigonométrica y haciendo cambios de variable.

${\displaystyle \begin{array}{l}\sin A-\sin B=2\left({\sin }^2\left(\frac{A}{2}+\frac{\pi }{4}\right)-{\sin }^2\left(\frac{B}{2}+\frac{\pi }{4}\right)\right)\\ {\displaystyle \underset{0}{\overset{{\phi }_0}{\int }}\frac{d\phi }{\sqrt{\text{sin}{\phi }_0-\text{sin}\phi }}}=\frac{1}{\sqrt{2}}{\displaystyle \underset{\pi /2}{\overset{{\phi }_0+\pi /2}{\int }}\frac{d\phi }{\sqrt{{\text{sin}}^2\left(\frac{{\phi }_0}{2}+\frac{\pi }{4}\right)-{\text{sin}}^2\left(\frac{\phi }{2}+\frac{\pi }{4}\right)}}}=\\ \frac{1}{\sqrt{2}}{\displaystyle \underset{\pi /2}{\overset{{\phi }_0+\pi /2}{\int }}\frac{d\theta }{\sqrt{{\text{sin}}^2\left(\frac{{\phi }_0}{2}+\frac{\pi }{4}\right)-{\text{sin}}^2\left(\frac{\theta }{2}\right)}}}\end{array}}$

Se ha efectuado el cambio de variable θ=φ+π/2. El segundo cambio de variable es

${\displaystyle \begin{array}{l}\text{sin}\varphi =\frac{\text{sin}\left(\theta /2\right)}{k}k=\text{sin}\left(\frac{{\phi }_0}{2}+\frac{\pi }{4}\right)\\ d\theta =\frac{2k\cos \varphi ·d\varphi }{\sqrt{1-k^2{\text{sin}}^2\varphi }}\\ {\displaystyle \underset{0}{\overset{{\phi }_0}{\int }}\frac{d\phi }{\sqrt{\text{sin}{\phi }_0-\text{sin}\phi }}}=\sqrt{2}{\displaystyle \underset{{\varphi }_0}{\overset{\pi /2}{\int }}\frac{d\varphi }{\sqrt{1-k^2{\text{sin}}^2\varphi }}}=\\ =\sqrt{2}\left({\displaystyle \underset{0}{\overset{\pi /2}{\int }}\frac{d\varphi }{\sqrt{1-k^2{\text{sin}}^2\varphi }}}-{\displaystyle \underset{0}{\overset{{\varphi }_0}{\int }}\frac{d\varphi }{\sqrt{1-k^2{\text{sin}}^2\varphi }}}\right)\text{sin}{\varphi }_0=\frac{\text{sin}(\pi /4)}{k}\end{array}}$

Procedimiento de cálculo

Cálculo de φ₀.

En primer lugar, calculamos el ángulo φ₀ que forma la recta tangente a la barra en su extremo libre con la parte negativa del eje horizontal X, tal como se ve en la figura anterior. Requiere resolver la ecuación trascendente, donde el símbolo E representa a integrales elípticas

${\displaystyle \begin{array}{l}{\displaystyle \underset{0}{\overset{\pi /2}{\int }}\frac{d\varphi }{\sqrt{1-k^2{\text{sin}}^2\varphi }}}-{\displaystyle \underset{0}{\overset{{\varphi }_0}{\int }}\frac{d\varphi }{\sqrt{1-k^2{\text{sin}}^2\varphi }}}=\sqrt{2\alpha }\\ \text{con}k=\sin \left(\frac{{\phi }_0}{2}+\frac{\pi }{4}\right)\sin {\varphi }_0=\frac{\sin (\pi /4)}{k}\end{array}}$

El programa interactivo al final de esta página, calcula las integrales elípticas de primera especie E(k, φ) mediante el procedimiento de Carlson. Véase Numerical Recipes in C, Special functions. Capítulo 6º. La raíz de la ecuación trascendente se obtiene por el procedimiento del punto medio.

Cálculo de las coordenadas (x/L, y/L) de cada punto de la barra deformada

El cálculo de x/L no reviste dificultad alguna. Conocido φ₀, se calcula x/L para cada ángulo φ en el intervalo (0,  φ₀).

${\displaystyle \frac{x}{L}=\frac{1}{\sqrt{\alpha }}\left(\sqrt{\sin {\phi }_0}-\sqrt{\sin {\phi }_0-\sin \phi }\right)}$

El cálculo de y/L es más problemático. Conocido φ₀, se determina la ordenada y/L para cada ángulo φ en el intervalo (0,  φ₀) calculando la integral definida,

${\displaystyle \frac{y}{L}=\frac{1}{2\sqrt{\alpha }}{\displaystyle \underset{0}{\overset{\phi }{\int }}\frac{\text{sin}\phi ·d\phi }{\sqrt{\text{sin}{\phi }_0-\text{sin}\phi }}}}$

por procedimientos numéricos

alfa=1.25;
f=@(x) ellipke(sin(x/2+pi/4)^2)-
ellipticF(asin(sin(pi/4)/sin(x/2+pi/4)),sin(x/2+pi/4)^2)-sqrt(2*alfa);
angFinal=fzero(f,[0,2]);
delta=angFinal/100;
xp=zeros(0,101);
yp=zeros(0,101);
xp(1)=0;
yp(1)=0;
i=1;
f=@(x) sin(x)./sqrt(sin(angFinal)-sin(x));
for ang=delta:delta:angFinal;
    i=i+1;
    xp(i)=(sqrt(sin(angFinal))-sqrt(sin(angFinal)-sin(ang)))/sqrt(alfa);
    yp(i)=integral(f,0, ang)/(2*sqrt(alfa));
end
plot(xp,yp)
xlim([0,0.8])
axis equal
grid on
set(gca,'YDir','reverse')
xlabel('x')
ylabel('y')
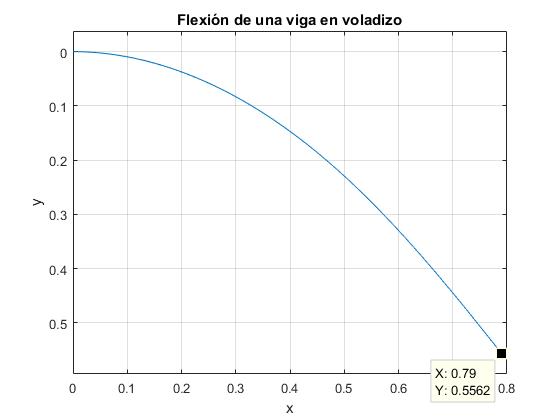
title('Flexión de una viga en voladizo')

El programa interactivo al final de esta página, cuando φ→φ₀ el denominador de la integral tiende a cero. El ordenador no calcula correctamente la ordenada y_f/L del extremo libre de la barra cuando φ=φ₀. Para solucionar este inconveniente, empleamos el procedimiento de interpolación que se muestra en la figura.

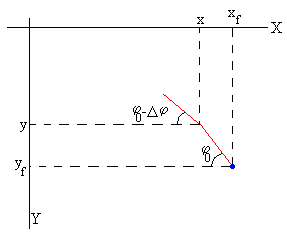
• Calculamos las coordenadas (x/L, y/L) para el ángulo φ=φ₀-Δφ, siendo Δφ un ángulo pequeño
• Calculamos la abscisa x_f/L para el ángulo φ₀

${\displaystyle \frac{x_f}{L}=\sqrt{\frac{\sin {\phi }_0}{\alpha }}}$

• La ordenada y_f/L se obtiene resolviendo el triángulo rectángulo de la figura

${\displaystyle \frac{y_f}{L}=\frac{y}{L}+\left(\frac{x_f}{L}-\frac{x}{L}\right)\tan {\phi }_0}$

Si ocurriera este caso, el script se modificaría en la representación gráfica.

%....
for ang=delta:delta:angFinal-delta;
    i=i+1;
    xp(i)=(sqrt(sin(angFinal))-sqrt(sin(angFinal)-sin(ang)))/sqrt(alfa);
    yp(i)=integral(f,0, ang)/(2*sqrt(alfa));
end
%interpolación
xf=sqrt(sin(angFinal))/sqrt(alfa);
yp(i+1)=yp(i)+(xf-xp(i))*tan(angFinal);
xp(i+1)=xf;
%....

Aproximación de pequeñas flexiones

Para pequeñas flexiones cuando el ángulo φ₀ es pequeño. Sustituimos sinφ≈φ y escribimos la ecuación que calcula φ₀.

${\displaystyle {\displaystyle \underset{0}{\overset{{\phi }_0}{\int }}\frac{d\phi }{\sqrt{{\phi }_0-\phi }}}=2\sqrt{\alpha }}$

El resultado es φ₀=α

Las coordenadas (x, y) de cada punto de la barra se aproximan a

${\displaystyle \frac{x}{L}=1-\sqrt{1-\frac{\phi }{\alpha }}}$

Para el extremos libre de la barra, cuando φ= φ₀=α, x_f=L, lo que implica que en la aproximación de pequeñas flexiones, no hay desplazamiento horizontal del extremo libre de la barra.

Aproximamos la ordenada y

${\displaystyle \frac{y}{L}=\frac{1}{2\sqrt{\alpha }}{\displaystyle \underset{0}{\overset{\phi }{\int }}\frac{\phi ·d\phi }{\sqrt{\alpha -\phi }}}}$

Integrando por partes y después de hacer algunas simplificaciones obtenemos la siguiente expresión

${\displaystyle \frac{y}{L}=\frac{2}{3}\left(\alpha -\left(\frac{\phi }{2}+\alpha \right)\sqrt{1-\frac{\phi }{\alpha }}\right)}$

Las coordenadas x e y, las hemos expresado en función del parámetro φ, eliminando el parámetro obtenemos la función y=f(x) que describe la flexión de la barra cuando se aplica una fuerza F en su extremo libre.

${\displaystyle \frac{y}{L}=\alpha \left(\frac{x^2}{L^2}-\frac{1}{3}\frac{x^3}{L^3}\right)y=\frac{FL}{2Y·I}\left(x^2-\frac{x^3}{3L}\right)}$

Para el extremos libre de la barra, cuando φ= φ₀=α, x=L,

${\displaystyle \frac{y_f}{L}=\frac{2}{3}\alpha y_f=\frac{1}{3}\frac{L^3}{Y·I}F}$

Límite de la aproximación de pequeñas flexiones

En la figura, se muestra la desviación y_f/L del extremo libre de la barra en función del parámetro adimensional α.

${\displaystyle \frac{y_f}{L}=\frac{1}{2\sqrt{\alpha }}{\displaystyle \underset{0}{\overset{{\phi }_0}{\int }}\frac{\text{sin}\phi ·d\phi }{\sqrt{\text{sin}{\phi }_0-\text{sin}\phi }}}}$

• En color azul, los resultados del cálculo, empleando procedimientos numéricos, descrito en el apartado anterior
• En color rosa, la recta y/L=2α/3, aproximación de pequeñas flexiones

xp=zeros(0,50);
yp=zeros(0,50);
xp(1)=0;
yp(1)=0;
i=1;
for alfa=0.1:1.5/50:1.5;
    f=@(x) ellipke(sin(x/2+pi/4)^2)
-ellipticF(asin(sin(pi/4)/sin(x/2+pi/4)),sin(x/2+pi/4)^2)-sqrt(2*alfa);
    angFinal=fzero(f,[0,2]);
    f=@(x) sin(x)./sqrt(sin(angFinal)-sin(x));
    i=i+1;
    xp(i)=alfa;
    yp(i)=integral(f,0, angFinal)/(2*sqrt(alfa));
end
plot(xp,yp, xp, 2*xp/3)
grid on
xlabel('\alpha')
ylabel('y')
title('Flexión de una viga en voladizo')

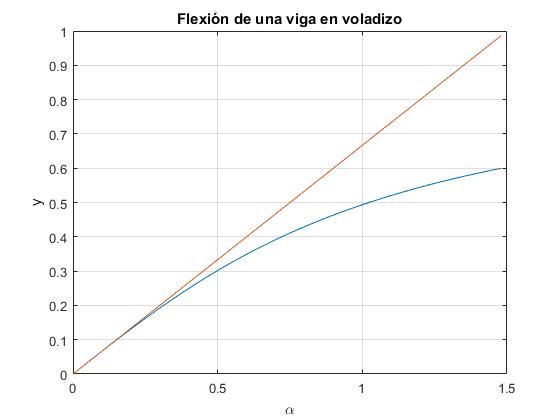
Podemos considerar, que la aproximación lineal produce resultados aceptables hasta un cierto valor límite del parámetro α_m o bien, hasta un cierto valor máximo de la fuerza aplicada F_m en el extremos libre de la barra

${\displaystyle F_m=\frac{2Y·I·{\alpha }_m}{L^2}}$

Actividades

Se introduce

• El parámetro adimensional α, proporcional a la fuerza F sobre el extremo libre,en el control titulado α (alfa)

Se pulsa el botón titulado Nuevo

Se representa una barra de longitud L=1 m deformada por la fuerza F aplicada en su extremo libre. Se proporcionan los datos de las coordenadas (x_f, y_f) de dicho punto y el ángulo φ₀, que forma la recta tangente a la barra en su extremo libre con el eje horizontal X.

Ejemplo

Sea una regla de acero de longitud L=30 cm, sección rectangular b=3.04 cm, y c=0.078 cm. El módulo de Young es Y=2.06·10¹¹ N/m²

El momento de inercia I vale

${\displaystyle I=\frac{b{c}^3}{12}=1.20·{10}^{-12}{\text{ m}}^{\text{4}}}$

Cuando aplicamos en el extremo libre de la barra una fuerza tal que α=0.25, es decir

${\displaystyle \alpha =\frac{F{L}^2}{2Y·I}F=1.38\text{ N}}$

observamos en el programa interactivo que se encuentra en x_f/L=0.98 e y_f/L=0.16, es decir, a x_f=29 cm, e y_f=4.8 cm del extremo fijo.

Aplicando la aproximación de pequeñas flexiones

${\displaystyle \frac{y_f}{L}=\frac{2}{3}\alpha y_f=\frac{1}{3}\frac{L^3}{Y·I}F=\frac{1}{3}\frac{{0.3}^3}{2.06·{10}^{11}·1.2·{10}^{-12}}1.38=0.05\text{m}=5.0\text{cm}}$

En la aproximación de pequeñas flexiones x_f≈L, no hay desviación apreciable en sentido horizontal y la desviación en sentido vertical y_f es proporcional a la fuerza F aplicada en el extremo libre.

Cuando aplicamos en el extremo libre de la barra una fuerza tal que α=1.25, es decir

${\displaystyle \alpha =\frac{F{L}^2}{2Y·I}F=6.88\text{N}}$

observamos en el programa interactivo que se encuentra en x_f/L=0.79 e y_f/L=0.56.

Aplicando la aproximación de pequeñas flexiones

${\displaystyle y_f=\frac{1}{3}\frac{L^3}{Y·I}F=\frac{1}{3}\frac{{0.3}^3}{2.06·{10}^{11}·1.2·{10}^{-12}}6.88=0.25\text{m}=\text{25}\text{cm}}$

En la aproximación de pequeñas flexiones deja de ser válida ya que hay una desviación apreciable en sentido horizontal y la desviación en sentido vertical y_f ya no es proporcional al a la fuerza F aplicada en el extremo libre.

Referencias

Feynman, Leighton, Sands. The Feynman Lectures on Physics V-II. Edt. Fondo Educativo Interamericano, págs. 38.15-17.

Beléndez T., Neipp C., Beléndez A., Flexión de una barra delgada empotrada en un extremo: Aproximación para pequeñas pendientes. Revista Brasileira de Ensino de Física. 24 (4) Dezembro 2002, págs, 399- 407.

Beléndez T., Neipp C., Beléndez A., Large and small defections of a cantilever beam. Eur. J. Phys. 23 (2002) pp. 371-379