Consideremos un cable de masa m y longitud L que cuelga del dos puntos situados a la misma altura, que distan 2a. Du densidad no es constante, viene descrito por la función λ(s), siendo s la longitud del arco. Supondremos que el cable es simétrico respecto del eje Y

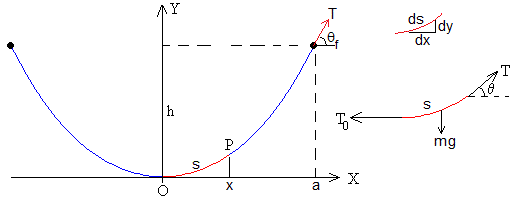
En la figura, se representa las fuerzas que actúan sobre una porción s de cable que tiene como origen el punto más bajo O:

• el peso, mg
• la fuerza T₀, que ejerce la parte izquierda del cable sobre el extremo izquierdo O de dicho segmento
• la fuerza T, que ejerce la parte derecha del cable sobre el extremo derecho P .

La condición de equilibrio se escribe

Tcosθ=T₀
Tsinθ=mg

Eliminando la tensión T

${\displaystyle \tan \theta =\frac{dy}{dx}=\frac{mg}{T_0}}$

En el extremo x=a del cable

${\displaystyle \begin{array}{l}\tan {\theta }_f={\frac{dy}{dx}|}_{x=a}\\ \frac{mg}{T_0}={\frac{dy}{dx}|}_{x=a},T_0=\frac{mg}{{\frac{dy}{dx}|}_{x=a}}\end{array}}$

La tensión T₀ se puede obtener a partir del ángulo θ_f que forma la tangente al cable en su extremo x=a

La masa m de la longitud s del cable de densidad λ(s) es

${\displaystyle m={\displaystyle \underset{0}{\overset{s}{\int }}\lambda (s)·ds}={\displaystyle \underset{0}{\overset{x}{\int }}\mu (x)·dx}}$

Relacionamos las dos densidades lineales

${\displaystyle \begin{array}{l}ds=\sqrt{d{x}^2+d{y}^2}=\sqrt{1+{\left(\frac{dy}{dx}\right)}^2}dx\\ \mu ·dx=\lambda ·ds\\ \mu =\lambda \sqrt{1+{\left(\frac{dy}{dx}\right)}^2}\end{array}}$

Por otra parte,

${\displaystyle \begin{array}{l}\frac{dy}{dx}=\frac{g}{T_0}{\displaystyle \underset{0}{\overset{x}{\int }}\mu (x)·dx}\\ \frac{d^{2}y}{d{x}^2}=\frac{g}{T_0}\mu (x)\\ \mu (x)=\frac{T_0}{g}\frac{d^{2}y}{d{x}^2}\\ \lambda =\frac{T_0}{g}\frac{\frac{d^{2}y}{d{x}^2}}{\sqrt{1+{\left(\frac{dy}{dx}\right)}^2}}\end{array}}$

La longitud s del cable es

${\displaystyle s={\displaystyle \underset{0}{\overset{x}{\int }}\sqrt{1+{\left(\frac{dy}{dx}\right)}^2}dx}}$

Dada la forma del cable y(x), estas dos últimas fórmulas nos permiten expresar la densidad λ en función de la longitud del arco s, tal como veremos en los siguientes ejemplos

Catenaria

Sea la función y(x)

${\displaystyle y=\frac{1}{\gamma }\left\{\cosh \left(\gamma x\right)-\cosh \left(\gamma a\right)\right\},\gamma =\frac{\lambda g}{T_0}}$

La derivada primera y la derivada segunda son, respectivamente

${\displaystyle \begin{array}{l}\frac{dy}{dx}=\sinh \left(\gamma x\right)\\ \frac{d^{2}y}{d{x}^2}=\frac{\lambda g}{T_0}\cosh \left(\gamma x\right)\end{array}}$

La densidad, λ es constante

${\displaystyle \lambda =\frac{T_0}{g}\frac{\frac{d^{2}y}{d{x}^2}}{\sqrt{1+{\left(\frac{dy}{dx}\right)}^2}}=\frac{T_0}{g}\frac{\frac{\lambda g}{T_0}\cosh \left(\gamma x\right)}{\sqrt{1+{\sinh }^2\left(\gamma x\right)}}=\lambda }$

La relación entre el arco s y la abscisa x es

${\displaystyle s={\displaystyle \underset{0}{\overset{x}{\int }}\sqrt{1+{\left(\frac{dy}{dx}\right)}^2}dx}={\displaystyle \underset{0}{\overset{x}{\int }}\sqrt{1+{\sinh }^2\left(\gamma x\right)}dx}={\displaystyle \underset{0}{\overset{x}{\int }}\cosh \left(\gamma x\right)·dx}=\frac{1}{\gamma }\sinh \left(\gamma x\right)}$

Cuando x=a entonces s=L/2

${\displaystyle \frac{L}{2}=\frac{1}{\gamma }\sinh \left(\gamma a\right)}$

Dada la longitud L del cable, calculamos la constante γ resolviendo esta ecuacicón transcendente

Semicircunferencia

Consideremos un cable en forma de semicircunferencia de radio a. La longitud del cable es L=πa

${\displaystyle \begin{array}{l}{x}^2+{\left(y-a\right)}^2=a^2\\ y=a-\sqrt{a^2-x^2}\end{array}}$

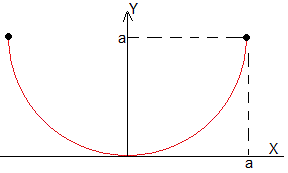
La derivada primera y la derivada segunda son, respectivamente

${\displaystyle \begin{array}{l}\frac{dy}{dx}=\frac{x}{\sqrt{a^2-x^2}}\\ \frac{d^{2}y}{d{x}^2}=\frac{a^2}{{\left(a^2-x^2\right)}^{3/2}}\end{array}}$

La densidad, λ ya no es constante

${\displaystyle \lambda =\frac{T_0}{g}\frac{\frac{d^{2}y}{d{x}^2}}{\sqrt{1+{\left(\frac{dy}{dx}\right)}^2}}=\frac{T_0}{g}\frac{\frac{a^2}{{\left(a^2-x^2\right)}^{3/2}}}{\sqrt{1+\frac{x^2}{a^2-x^2}}}=\frac{T_0}{g}\frac{a}{a^2-x^2}}$

La relación entre el arco s y la abscisa x es

${\displaystyle \begin{array}{l}s={\displaystyle \underset{0}{\overset{x}{\int }}\sqrt{1+{\left(\frac{dy}{dx}\right)}^2}dx}\\ s=a{\displaystyle \underset{0}{\overset{x}{\int }}\frac{dx}{\sqrt{a^2-x^2}}=a·\arcsin \left(\frac{x}{a}\right)}\\ x=a\sin \left(\frac{s}{a}\right)\end{array}}$

La densidad del cable es

${\displaystyle \begin{array}{l}\lambda =\frac{T_0}{g}\frac{a}{a^2-x^2}=\frac{T_0}{g}\frac{a}{a^2-a^2{\sin }^2\left(\frac{s}{a}\right)}\\ \lambda (s)=\frac{T_0}{ga}\frac{1}{{\cos }^2\left(\frac{s}{a}\right)}\end{array}}$

Al final de la página, estudiamos con más detalle este ejemplo

Parábola, y=k·x²

Consideremos un cable en forma de parábola, y=k·x²

La derivada primera y la derivada segunda son, respectivamente

${\displaystyle \begin{array}{l}\frac{dy}{dx}=2kx\\ \frac{d^{2}y}{d{x}^2}=2k\end{array}}$

La densidad, λ ya no es constante

${\displaystyle \begin{array}{l}\lambda =\frac{T_0}{g}\frac{\frac{d^{2}y}{d{x}^2}}{\sqrt{1+{\left(\frac{dy}{dx}\right)}^2}}=\frac{T_0}{g}\frac{2k}{\sqrt{1+{\left(2kx\right)}^2}}\\ \lambda =\frac{m}{{\frac{dy}{dx}|}_{x=a}}\frac{2k}{\sqrt{1+{\left(2kx\right)}^2}}=\frac{m}{2ka}\frac{2k}{\sqrt{1+{\left(2kx\right)}^2}}=\frac{m}{a\sqrt{1+{\left(2kx\right)}^2}}\end{array}}$

La relación entre el arco s y la abscisa x es

${\displaystyle \begin{array}{l}s={\displaystyle \underset{0}{\overset{x}{\int }}\sqrt{1+{\left(2kx\right)}^2}dx}=2k{\displaystyle \underset{0}{\overset{x}{\int }}\sqrt{\frac{1}{4k^2}+x^2}dx}\\ \{\begin{array}{l}x=\frac{1}{2k}\sinh u\\ dx=\frac{1}{2k}\cosh u·du\end{array}\\ {\displaystyle \int \sqrt{\frac{1}{4k^2}+x^2}dx=\frac{1}{4k^2}{\displaystyle \int {\cosh }^{2}u·du}}=\frac{1}{4k^2}{\displaystyle \int \frac{1+\cosh \left(2u\right)}{2}du}=\frac{1}{8k^2}\left(u+\frac{1}{2}\sinh \left(2u\right)\right)\\ s=\frac{1}{4k}\left(u+\sinh u·\cosh u\right)=\frac{1}{4k}\left(\text{arcsinh}\left(2kx\right)+2kx\sqrt{1+4k^2{x}^2}\right)\end{array}}$

Comparación

Consideremos un cable de longitud L=πa, suspendido de dos puntos a la misma altura separados 2a

Tomamos a=1

Para la catenaria, dada la longitud L del cable, calculamos el parámetro γ resolviendo la ecuación transcedente

${\displaystyle \frac{L}{2}=\frac{1}{\gamma }\sinh \left(\gamma a\right)}$

A continuación, representamos la curva y(x)

Para el cable en forma de semicircunferencia, representamos la semicircunferencia de radio a=1

Para el cable en forma de parábola, dada la longitud L=πa del cable, calculamos el parámetro k resolviendo la ecuación transcedente

${\displaystyle \frac{L}{2}=\frac{1}{4k}\left(\text{arcsinh}\left(2ka\right)+2ka\sqrt{1+4k^2{a}^2}\right)}$

A continuación, representamos la parábola y=k·x²

a=1; %la distancia  es 2a
L=pi*a; %longitud
hold on
%catenaria
f=@(x) sinh(a*x)-L*x/2;
gamma=fzero(f,[0.1 10]);
f=@(x) (cosh(gamma*x)-cosh(gamma*a))/gamma;
fplot(f,[-a,a]);
%semicircunferencia
fplot(@(t) a*cos(t), @(t) a*sin(t),[pi,2*pi])
%parábola
f=@(x) asinh(2*a*x)+2*a*x*sqrt(1+4*x^2*a^2)-2*x*L;
k=fzero(f,[0.1 10]);
fplot(@(x) k*x.^2-k*a^2,[-a,a]);
hold off
axis equal
grid on
legend('catenaria','semicircunferencia','parábola')
xlabel('x');
ylabel('y');
title('Catenarias')

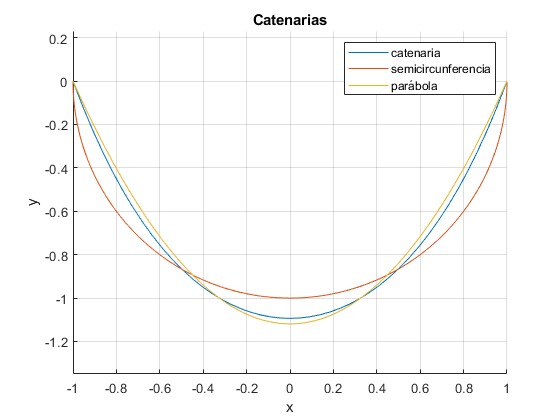
La catenaria y la parábola no son fáciles de distinguir a primera vista

Para el cable en forma de parábola, la constante k=1.1189

>> k
k =    1.1189

Densidad λ de la parábola

Representamos λ/m en función de s desde 0 a L/2=πa/2 para la parábola con k=1.1189.

Dado s en el intervalo [0, πa/2] calculamos la abscisa x resolviendo la ecuación transcendente

${\displaystyle \text{arcsinh}\left(2kx\right)+2kx\sqrt{1+4k^2{x}^2}-4ks=0}$

Dado x correspondiente a s, calculamos λ/m

${\displaystyle \frac{\lambda }{m}=\frac{1}{a\sqrt{1+{\left(2kx\right)}^2}}}$

a=1; %la distancia  es 2a
L=pi*a; %longitud del camble
hold on
%parábola
k=1.1189;
ss=linspace(0,L/2,100);
xx=zeros(1,length(ss));
i=1;
for s=ss
    f=@(x) asinh(2*k*x)+2*k*x*sqrt(1+4*k^2*x^2)-4*k*s;
    xx(i)=fzero(f,[0,L/2]);
    i=i+1;
end
g=@(x) 1./(a*sqrt(1+(2*k*x).^2));
plot(ss,g(xx));
hold off
grid on
xlabel('s');
ylabel('\lambda/m');
title('Densidad')

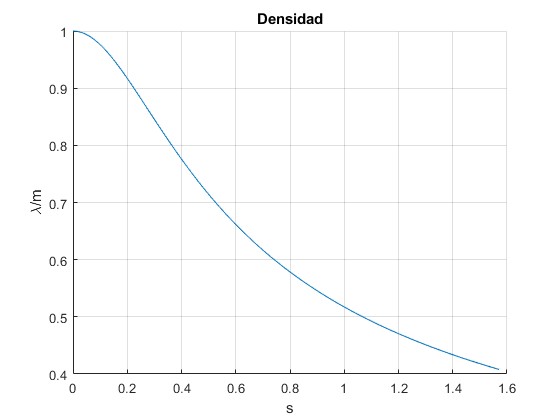
La densidad λ de la catenaria es constante

Semicircunferencia

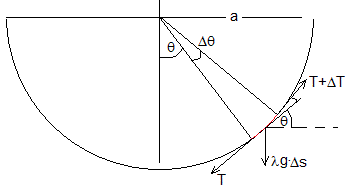
Consideremos un elemento diferencial de cable de longitud Δs. Las fuerzas que actúan son

• El peso, λ·g·Δs, siendo λ la densidad lineal kg/m
• La fuera T+ΔT que ejerce la parte derecha del cable sobre dicho elemento, cuya direccion es tangente al cable en la posición θ+Δθ
• La fuera T que ejerce la parte izquierda del cable sobre dicho elemento, cuya direccion es tangente al cable en la posición θ

Descomponiendo estas fuerzas en la dirección tangente y normal

${\displaystyle \begin{array}{l}\{\begin{array}{l}\left(T+\Delta T\right)\cos \left(\Delta \theta \right)=T+\lambda g\Delta s·\sin \theta \\ \left(T+\Delta T\right)\sin \left(\Delta \theta \right)=\lambda g\Delta s·\cos \theta \end{array}\\ \Delta \theta \to \mathrm{0,}\{\begin{array}{l}dT=\lambda gds·\sin \theta \\ T·d\theta =\lambda gds·\cos \theta \end{array}\end{array}}$

Integrando

${\displaystyle \begin{array}{l}\frac{dT}{T}=\frac{\sin \theta }{\cos \theta }d\theta \\ \ln T=-\ln \left(\cos \theta \right)+\ln T_0\\ T=\frac{T_0}{\cos \theta }\end{array}}$

T₀ es la constante de integración, la tensión del cable para θ=0

Para determinar la densidad lineal del cable, despejamos la tensión T

${\displaystyle T=\lambda g\cos \theta ·\frac{ds}{d\theta }}$

En una circunferencia, el arco ds=a·dθ, siendo a el radio

${\displaystyle \begin{array}{l}T=\lambda ga\cos \theta \\ \lambda =\frac{T_0}{ga·{\cos }^2\theta }\end{array}}$

El mismo resultado

Semicircunferencia discreta

Supongamos una cadena formada por eslabones (segmento de color azul entre dos puntos de color rojo) de longitud d, de masa despreciable. En el medio del eslabón k se coloca una partícula (en azul) de masa m_k distinta para cada eslabón.

En el ejemplo estudiado en la página titulada catenaria los eslabones tenían la misma masa. Como en el ejemplo estudiado, la cadena es simétrica respecto del eje vertical Y

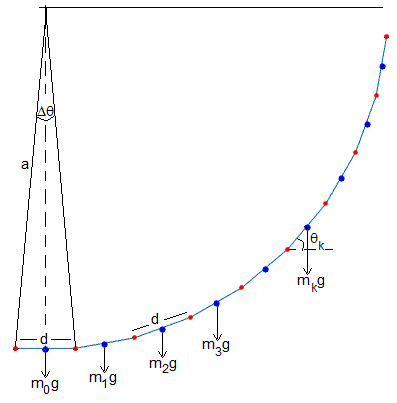
Representamos las fuerzas sobre el primer eslabón, el segundo y el tercero

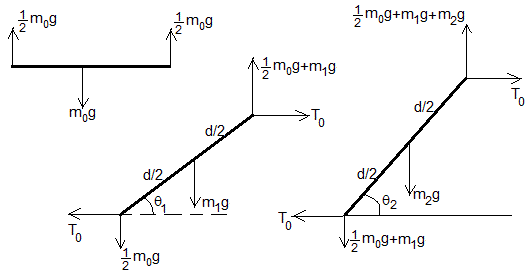
Los momentos de las fuerzas del segundo y tercer eslabón, respecto del extremo inferior izquierdo, nos permiten determinar los ángulos θ₁ y θ₂

Segundo eslabón

${\displaystyle \begin{array}{l}\left(\frac{1}{2}{m}_{0}g+m_{1}g\right)d\cos {\theta }_1=T_{0}d\sin {\theta }_1+m_{1}g\frac{d}{2}\cos {\theta }_1\\ \frac{1}{2}\left(m_0+m_1\right)g\cos {\theta }_1=T_0\sin {\theta }_1\\ \tan {\theta }_1=\frac{\frac{1}{2}\left(m_0+m_1\right)g}{T_0}\end{array}}$

Tercer eslabón

${\displaystyle \begin{array}{l}\left(\frac{1}{2}{m}_{0}g+m_{1}g+m_{2}g\right)d\cos {\theta }_2=T_{0}d\sin {\theta }_2+m_{2}g\frac{d}{2}\cos {\theta }_2\\ \frac{1}{2}\left(m_0+2m_1+m_2\right)g\cos {\theta }_2=T_0\sin {\theta }_2\\ \tan {\theta }_2=\frac{\frac{1}{2}\left(m_0+2m_1+m_2\right)g}{T_0}\end{array}}$

En general, eslabón k

${\displaystyle \begin{array}{l}\left(\frac{1}{2}{m}_{0}g+m_{1}g+m_{2}g+\mathrm{...}+m_{k}g\right)d\cos {\theta }_k=T_{0}d\sin {\theta }_k+m_{k}g\frac{d}{2}\cos {\theta }_k\\ \frac{1}{2}\left(m_0+2m_1+2m_2+\mathrm{...}+m_k\right)g\cos {\theta }_k=T_0\sin {\theta }_k\\ \tan {\theta }_k=\frac{\frac{1}{2}\left(m_0+2m_1+2m_2+\mathrm{...}+m_k\right)g}{T_0}\end{array}}$

La masa m_k del eslabón es el producto de la densidad lineal por su longitud d

${\displaystyle \begin{array}{l}{m}_k=\frac{T_0}{ga{\cos }^2{\theta }_k}d\\ d=2a\sin \left(\frac{\Delta \theta }{2}\right)\end{array}}$

Los ángulos θ_k valen

${\displaystyle \begin{array}{l}\tan {\theta }_k=\frac{\frac{1}{2}\left(m_0+2m_1+2m_2+\mathrm{...}+m_k\right)g}{T_0}\\ \tan {\theta }_k=\left(\frac{1}{{\cos }^{2}0}+\frac{2}{{\cos }^2{\theta }_1}+\frac{2}{{\cos }^2{\theta }_2}+\mathrm{...}+\frac{1}{{\cos }^2{\theta }_k}\right)\sin \left(\frac{\Delta \theta }{2}\right)\end{array}}$

Teniendo en cuenta la relación trigonométrica, $\frac{1}{{\cos }^2\theta }=1+{\tan }^2\theta$. Para calcular cada uno de los ángulos θ₁, θ₂...θ_k se resuelven las ecuaciones de segundo grado

${\displaystyle \{\begin{array}{l}\tan {\theta }_1=\left(2+{\tan }^2{\theta }_1\right)\sin \left(\frac{\Delta \theta }{2}\right)\\ \tan {\theta }_2=\left(4+2{\tan }^2{\theta }_1+{\tan }^2{\theta }_2\right)\sin \left(\frac{\Delta \theta }{2}\right)\\ \tan {\theta }_3=\left(6+2{\tan }^2{\theta }_1+2{\tan }^2{\theta }_2+{\tan }^2{\theta }_3\right)\sin \left(\frac{\Delta \theta }{2}\right)\\ \mathrm{...}\\ \tan {\theta }_k=\left(2k+2{\tan }^2{\theta }_1+2{\tan }^2{\theta }_2+\mathrm{...}+{\tan }^2{\theta }_k\right)\sin \left(\frac{\Delta \theta }{2}\right)\end{array}}$

La primera ecuación, calcula el ángulo θ₁. Conocido este ángulo, la segunda ecuación calcula θ₂ y así, sucesivamente. A continuación, representamos los eslabones

N=8; %eslabones
th=zeros(1,N);
d_th=pi/(2*(N+1)); % 10º
a=1; %radio
d=2*a*sin(d_th/2);
x2=d/2;
y2=-a*cos(d_th/2);
hold on
fplot(@(t) a*cos(t), @(t) a*sin(t),[-pi/2, 0],'k') %circunferencia
line([0,x2],[y2,y2]) %primer eslabón
plot(x2,y2,'ro','markersize',3,'markerfacecolor','r')
for k=1:N-1
    x1=x2;
    y1=y2;
    suma=2*k;
    for i=1:k-1
        suma=suma+2*tan(th(i))^2;
    end
    c=1/sin(d_th/2);
    th(k)=atan((c-sqrt(c^2-4*suma))/2);
    x2=x1+d*cos(th(k));
    y2=y1+d*sin(th(k));
    line([x1,x2],[y1,y2]) %eslabón k
    plot(x2,y2,'ro','markersize',3,'markerfacecolor','r')
end
hold off
ylim([-1,0])
axis equal

Para N=8 eslabones. En color negro, el arco de circunferencia de radio a

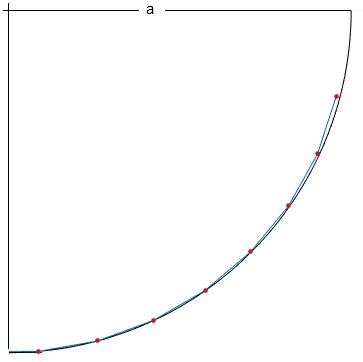
Para N=20 eslabones

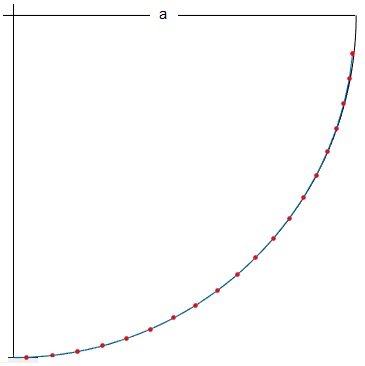
El ajuste de los eslabones al arco de circunferencia de radio a es casi perfecto, excepto los últimos que se desvían ligeramente

Referencias

P D S de Lima, J M de Araújo, M S Ferreira. Inverse design from the catenary problem. Eur. J. Phys. 45 (2024) 035007

Robert O'Keefe. A circular catenary. Am. J. Phys. 64 (5) May 1996, pp. 660-661