En la figura, se muestra la forma de un cable suspendido de dos puntos A y B situados en una superficie cilíndrica de radio R.

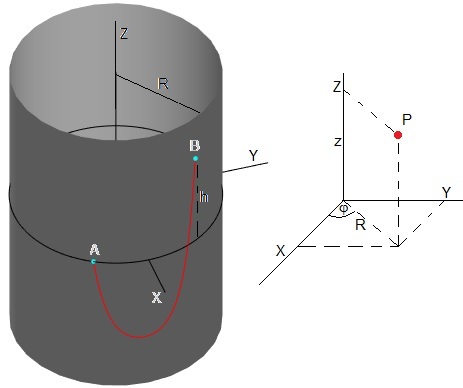
Un punto P sobre una superficie cilíndrica de radio R tiene coordenadas (φ, z), donde φ es el ángulo que forma con el eje X la línea que une el origen con la proyección de dicho punto sobre el plano XY. z es la altura del punto P sobre el plano XY. Por ejemplo, las coordenadas de A(-π/6,0) y las de B(π/6,1).

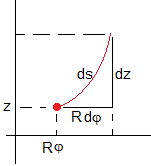
Una curva sobre la superficie cilíndrica viene descrita por la función z=z(φ)

La longitud ds de un arco diferencial de curva situada en el punto φ,z

${\displaystyle ds=\sqrt{d{z}^2+R^{2}d{\phi }^2}=\sqrt{R^2+{\left(\frac{dz}{d\phi }\right)}^2}d\phi }$

La longitud de un cable suspendido de los puntos A (-φ₀, 0) y B (φ₀, h) es

${\displaystyle L={\displaystyle \underset{-{\phi }_0}{\overset{{\phi }_0}{\int }}ds}={\displaystyle \underset{-{\phi }_0}{\overset{{\phi }_0}{\int }}\sqrt{R^2+{\left(\frac{dz}{d\phi }\right)}^2}d\phi }}$

La energía potencial de un pequeño arco de longitud ds del cable localizado en el punto (φ,z) es dm·gz. Su masa es dm=λ·ds, λ la densidad lineal en kg/m

La energía potencial del cable es

${\displaystyle E_p={\displaystyle \underset{-{\phi }_0}{\overset{{\phi }_0}{\int }}zg\lambda ds}=\lambda g{\displaystyle \underset{-{\phi }_0}{\overset{{\phi }_0}{\int }}z\sqrt{R^2+{\left(\frac{dz}{d\phi }\right)}^2}d\phi }}$

Tenemos que determinar la ecuación de la curva z=z(φ) que haga que la energía potencial del cable sea mínima, con la condición de que el cable tenga una longitud fija L.

Un problema similar isoperimétrico estudiado en la página titulada 'Cálculo de variaciones'. Definimos una función F dependiente de un parámetro k

${\displaystyle F\left(\phi ,z,\dot{z}\right)=\lambda gz\sqrt{R^2+{\dot{z}}^2}+k\sqrt{R^2+{\dot{z}}^2}=\left(\lambda gz+k\right)\sqrt{R^2+{\dot{z}}^2},\dot{z}=\frac{dz}{d\phi }}$

Aplicando la ecuación de Euler-Lagrange a la función F que no depende de φ

${\displaystyle \begin{array}{l}F-\dot{z}\frac{\partial F}{\partial \dot{z}}=C_1\\ \left(\lambda gz+k\right)\sqrt{R^2+{\dot{z}}^2}-\dot{z}\left(\lambda gz+k\right)\frac{\dot{z}}{\sqrt{R^2+{\dot{z}}^2}}=C_1\\ \frac{R^2}{\sqrt{R^2+{\dot{z}}^2}}=\frac{C_1}{\lambda gz+k}\\ \lambda gz+k=C_2\sqrt{R^2+{\left(\frac{dz}{d\phi }\right)}^2}\end{array}}$

Esta es la ecuación diferencial de un cable suppendido de dos puntos de una superficie cilíndrica. Elevando al cuadrado despejamos dz/dφ

${\displaystyle \frac{dz}{d\phi }=\sqrt{\frac{{\left(\lambda gz+k\right)}^2}{C_2^2}-R^2}}$

Integramos

${\displaystyle \frac{C_2}{\lambda g}{\displaystyle \int \frac{dz}{\sqrt{{\left(z+\frac{k}{\lambda g}\right)}^2-\frac{R^2{C}_2^2}{{\lambda }^2{g}^2}}}=\phi +C_3}}$

Haciendo el cambio de variable u=z+k/(λg), la integral es inmediata

${\displaystyle \begin{array}{l}u=z+\frac{k}{\lambda g},du=dz\\ \frac{C_2}{\lambda g}{\displaystyle \int \frac{du}{\sqrt{u^2-\frac{R^2{C}_2^2}{{\lambda }^2{g}^2}}}=\phi +C_3}\\ \frac{C_2}{\lambda g}\text{arccosh}\left(\frac{\lambda g}{R{C}_2}u\right)=\phi +C_3\\ \frac{C_2}{\lambda g}\text{arccosh}\left(\frac{\lambda gz+k}{R{C}_2}\right)=\phi +C_3\\ \frac{\lambda gz+k}{R{C}_2}=\cosh \left(\frac{\lambda g}{C_2}\left(\phi +C_3\right)\right)\\ z=\frac{R{C}_2}{\lambda g}\cosh \left(\frac{\lambda g}{C_2}\phi +\frac{\lambda g}{C_2}{C}_3\right)-\frac{k}{\lambda g}\end{array}}$

La ecuación de la catenaria depende de tres parámetros a, b y c que se determinan a partir de las coordenadas de los puntos A (-φ₀, 0), B (φ₀, h) y de la longitud L del cable

${\displaystyle z=aR\cosh \left(\frac{\phi +b}{a}\right)+c,\{\begin{array}{l}a=\frac{C_2}{\lambda g}\\ b=\frac{C_3}{a}\\ c=\frac{k}{\lambda g}\end{array}}$

• La longitud del cable es

${\displaystyle \begin{array}{l}L={\displaystyle \underset{-{\phi }_0}{\overset{{\phi }_0}{\int }}\sqrt{R^2+{\left(\frac{dz}{d\phi }\right)}^2}d\phi }={\displaystyle \underset{-{\phi }_0}{\overset{{\phi }_0}{\int }}\sqrt{R^2+R^2{\sinh }^2\left(\frac{\phi +b}{a}\right)}d\phi }=\\ R{\displaystyle \underset{-{\phi }_0}{\overset{{\phi }_0}{\int }}\cosh \left(\frac{\phi +b}{a}\right)d\phi }=Ra\sinh \left(\frac{{\phi }_0+b}{a}\right)-Ra\sinh \left(\frac{-{\phi }_0+b}{a}\right)\\ \frac{L}{aR}=\sinh \left(\frac{{\phi }_0+b}{a}\right)-\sinh \left(\frac{-{\phi }_0+b}{a}\right)\\ \frac{L}{aR}=2\sinh \left(\frac{{\phi }_0}{a}\right)\cosh \left(\frac{b}{a}\right)\end{array}}$

Para obtener la última ecuación hay que expresar el seno hiperbólico como diferencia de dos exponenciales

• Cable suspendido de los puntos A y B

${\displaystyle \begin{array}{l}\{\begin{array}{l}0=aR\cosh \left(\frac{-{\phi }_0+b}{a}\right)+c\\ h=aR\cosh \left(\frac{{\phi }_0+b}{a}\right)+c\end{array}\\ \frac{h}{aR}=\cosh \left(\frac{{\phi }_0+b}{a}\right)-\cosh \left(\frac{-{\phi }_0+b}{a}\right)\\ \frac{h}{aR}=2\sinh \left(\frac{b}{a}\right)\sinh \left(\frac{{\phi }_0}{a}\right)\end{array}}$

Habiendo eliminado el parámetro c del sistema de dos ecuaciones, nos quedan dos ecuaciones con dos incógnitas a y b

${\displaystyle \{\begin{array}{l}\frac{h}{2aR}=\sinh \left(\frac{b}{a}\right)\sinh \left(\frac{{\phi }_0}{a}\right)\\ \frac{L}{2aR}=\sinh \left(\frac{{\phi }_0}{a}\right)\cosh \left(\frac{b}{a}\right)\end{array}}$

Dividiendo

${\displaystyle \begin{array}{l}\frac{h}{L}=\tanh \left(\frac{b}{a}\right)\\ \frac{h}{L}=\frac{e^{b/a}-e^{-b/a}}{e^{b/a}+e^{-b/a}}\\ \frac{h}{L}=\frac{e^{2b/a}-1}{e^{2b/a}+1}\\ e^{2b/a}=\frac{L+h}{L-h}\\ b=\frac{a}{2}\ln \left(\frac{L+h}{L-h}\right)\end{array}}$

Elevando al cuadrado la segunda ecuación y empleando la relación cosh²x-sinh²x=1, obtenemos una ecuación transcendente en a

${\displaystyle \begin{array}{l}{\left(\frac{L}{2aR}\right)}^2={\sinh }^2\left(\frac{{\phi }_0}{a}\right)\left(1+{\sinh }^2\left(\frac{b}{a}\right)\right)\\ {\left(\frac{L}{2aR}\right)}^2={\sinh }^2\left(\frac{{\phi }_0}{a}\right)\left(1+{\left(\frac{\frac{h}{2aR}}{\sinh \left(\frac{{\phi }_0}{a}\right)}\right)}^2\right)\\ {\left(\frac{L}{2aR}\right)}^2={\sinh }^2\left(\frac{{\phi }_0}{a}\right)+{\left(\frac{h}{2aR}\right)}^2\\ 2aR\sinh \left(\frac{{\phi }_0}{a}\right)=\sqrt{L^2-h^2}\end{array}}$

Calculamos el parámetro a, luego b y por último c, de una de las dos ecuaciones del sistema

${\displaystyle 0=aR\cosh \left(\frac{-{\phi }_0+b}{a}\right)+c}$

Resumiendo, para determinar a, b y c empleamos las relaciones

${\displaystyle \{\begin{array}{l}2aR\sinh \left(\frac{{\phi }_0}{a}\right)=\sqrt{L^2-h^2}\\ b=\frac{a}{2}\ln \left(\frac{L+h}{L-h}\right)\\ c=-aR\cosh \left(\frac{-{\phi }_0+b}{a}\right)\end{array}}$

Ejemplo

Sea un cable de longitud L=3 m, suspendido de los puntos A(-π/6,0) y B(π/6, 1) situados en una superficie cilíndrica de radio R=0.5 m

La mayor dificultad estriba en determinar el valor del parámetro a. Para tener una idea de dónde se encuentra la raíz de la primera ecuación, representamos las funciones

${\displaystyle \begin{array}{l}f(y)=2R\sinh \left(y{\phi }_0\right),y=\frac{1}{a}\\ g(y)=y\sqrt{L^2-h^2}\end{array}}$

Una raíz es y=0. Para que exista una raíz y≠0, la pendiente de la recta ha de ser mayor que la pendiente de la función f(y) en el origen

${\displaystyle \begin{array}{l}{\frac{df(y)}{dy}|}_{y=0}={2R{\phi }_0\cosh \left(y{\phi }_0\right)|}_{y=0}=2R{\phi }_0\\ \sqrt{L^2-h^2}>2R{\phi }_0\end{array}}$

2Rφ₀ es la longitud del arco de circunferencia entre -φ₀ y φ₀

L=3; %longitud
R=0.5; %radio
phi_0=pi/6; %posición
h=1;
hold on
f=@(y) 2*R*sinh(phi_0*y);
g=@(y) sqrt(L^2-h^2)*y;
fplot(f,[0,10])
fplot(g,[0,10])
raiz=fzero(@(y) f(y)-g(y), [0.1,10]);
fprintf('El parámetro a=%1.4f\n',1/raiz)
line([raiz,raiz],[0, f(raiz)],'lineStyle','--')
hold off
ylim([0,40])
grid on
xlabel('y')
ylabel('f(y), g(y)')
title('Raíz de la ecuación transcendente')

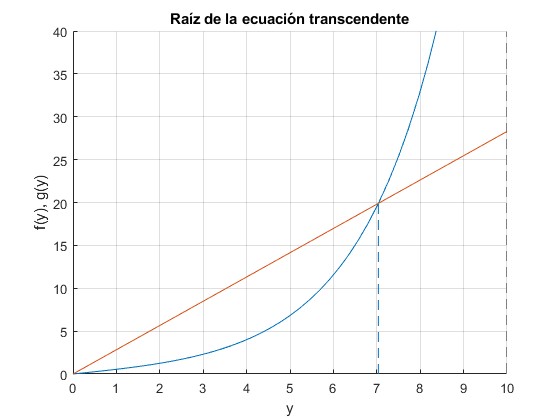
Vemos que la intersección se produce en y≈7, (a≈1/7). Calculamos la raíz con la función fzero de MATLAB.

El parámetro a=0.1421

Conocido el parámetro a calculamos b y c y representamos la catenaria

${\displaystyle \{\begin{array}{l}x=R\cos \phi \\ y=R\sin \phi \\ z=aR\cosh \left(\frac{\phi +b}{a}\right)+c\end{array}}$

L=3; %longitud
R=0.5; %radio
phi_0=pi/6; %posición de A
h=1; %altura de B

%parámetros a,b,c
f=@(y) 2*R*sinh(phi_0*y)-sqrt(L^2-h^2)*y;
a=1/fzero(f, [0.1,10]);
b=a*log((L+h)/(L-h))/2;
c=-a*R*cosh((-phi_0+b)/a);

%cilindro
r=R*ones(30,1);
phi=linspace(0,2*pi,30);
[r,phi]=meshgrid(r,phi);
x=r.*cos(phi);
y=r.*sin(phi);
z=repmat(linspace(-1.1,1.1,30),30,1);
hold on
surfl(x,y,z);
shading interp
colormap(gray);

%catenaria
X=@(t) R*cos(t);
Y=@(t) R*sin(t);
Z=@(t) a*R*cosh((t+b)/a)+c;
fplot3(X,Y,Z, [-phi_0,phi_0],'color','r')
plot3(R*cos(-phi_0),R*sin(-phi_0),0, 'co','markersize',3,'markerfacecolor','c')
plot3(R*cos(phi_0),R*sin(phi_0), h, 'co','markersize',3,'markerfacecolor','c')
%ejes
fplot3(@(t) R*cos(t), @(t) R*sin(t), @(t) t-1*t, [0,2*pi], 'color','k')
line([0,R+0.25],[0,0],[0,0], 'color','k')
line([0,0],[0,R+0.25],[0,0], 'color','k')
line([0,0],[0,0],[-1,1], 'color','k')

hold off
axis equal
xlabel('x'); ylabel('y'); zlabel('z')
title('Superficie cilíndrica')
view(70,40)

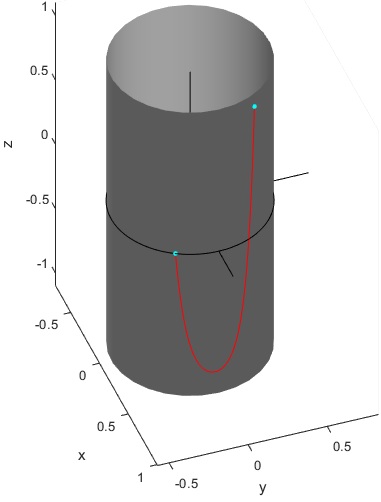
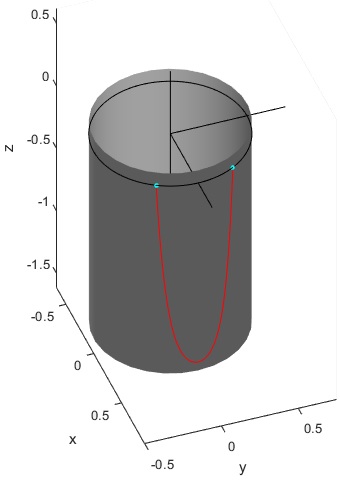
Catenaria simétrica

Cuando h=0, los puntos A y B están a la misma altura, la catenaria es simétrica y las fórmulas se reducen

${\displaystyle \{\begin{array}{l}2aR\sinh \left(\frac{{\phi }_0}{a}\right)=L\\ b=0\\ c=-aR\cosh \left(\frac{-{\phi }_0}{a}\right)=-aR\sqrt{1+{\sinh }^2\left(\frac{{\phi }_0}{a}\right)}=-\sqrt{{\left(aR\right)}^2+\frac{L^2}{4}}\end{array}}$

Las ecuaciones paramétricas de la catenaria son

${\displaystyle \{\begin{array}{l}x=R\cos \phi \\ y=R\sin \phi \\ z=aR\cosh \left(\frac{\phi }{a}\right)+c\end{array}}$

L=3; %longitud
R=0.5; %radio
phi_0=pi/6; %posición de A

%parámetros a,c
f=@(y) 2*R*sinh(phi_0*y)-L*y;
a=1/fzero(f, [0.1,10]);
c=-a*R*cosh(-phi_0/a);

%cilindro
r=R*ones(30,1);
phi=linspace(0,2*pi,30);
[r,phi]=meshgrid(r,phi);
x=r.*cos(phi);
y=r.*sin(phi);
z=repmat(linspace(-1.5,0.1,30),30,1);
hold on
surfl(x,y,z);
shading interp
colormap(gray);

%catenaria
X=@(t) R*cos(t);
Y=@(t) R*sin(t);
Z=@(t) a*R*cosh(t/a)+c;
fplot3(X,Y,Z, [-phi_0,phi_0],'color','r')
plot3(R*cos(-phi_0),R*sin(-phi_0),0, 'co','markersize',3,'markerfacecolor','c')
plot3(R*cos(phi_0),R*sin(phi_0), 0, 'co','markersize',3,'markerfacecolor','c')
%ejes
fplot3(@(t) R*cos(t), @(t) R*sin(t), @(t) t-1*t, [0,2*pi], 'color','k')
line([0,R+0.25],[0,0],[0,0], 'color','k') %eje X
line([0,0],[0,R+0.25],[0,0], 'color','k') %eje Y
line([0,0],[0,0],[-1,0.5], 'color','k') %eje Z

hold off
axis equal
xlabel('x'); ylabel('y'); zlabel('z')
title('Superficie cilíndrica')
view(70,40)

Referencias

E. G. M. de Lacerda, H. L. Carrión. A catenary-like cable confined in a circular cylinder. Revista Mexicana de Física, E 21 010211 1–10. January–June 2024