Composición de movimientos: traslación y rotación
Movimiento general de un sólido rígido
Un sólido fijo se caracteriza por ser indeformable, las posiciones relativas de los puntos del sólido se mantienen fijas aunque se apliquen fuerzas al mismo.
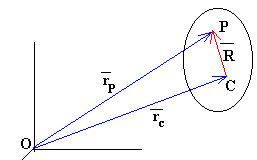
En la figura vemos que la posición del punto P del sólido es
Donde C se refiere al centro de masas del sólido. El vector que va del centro de masas al punto P es un vector cuyo módulo es constante.
Derivando la expresión anterior respecto del tiempo obtenemos
El primer término es la velocidad del punto P, el segundo la velocidad del centro de masas y el tercero es la velocidad del punto P respecto del centro de masas.
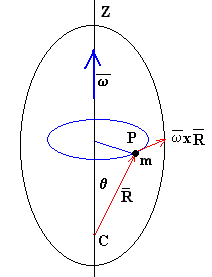
Dado que el vector tiene módulo constante, el único movimiento posible de P respecto de C es una rotación con velocidad angular alrededor de un eje instantáneo que pase por C, tal como vemos en la figura.
El movimiento de un punto P del sólido es la suma de un movimiento de traslación del centro de masa más una rotación alrededor de un eje instantáneo que pasa por el centro de masa.
Movimiento de rodar sin deslizar
En el movimiento de rodar sin deslizar, la rueda se traslada a la vez que gira.
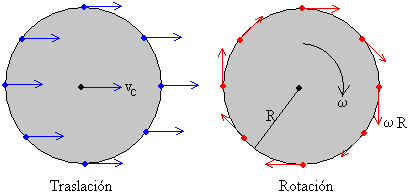
En el movimiento de traslación, todos los puntos del sólido se mueven en trayectorias paralelas. La velocidad de un punto del sólido es la misma que la velocidad del centro de masas.
En el movimiento de rotación alrededor de un eje que pasa por el centro de masas, la velocidad de un punto del sólido es proporcional la radio de la circunferencia que describe y su dirección es tangente a dicha circunferencia.
En el movimiento de rodar sin deslizar, existe una relación entre el movimiento de rotación y traslación. El punto P de la rueda que está en contacto en un instante dado con el suelo tiene velocidad nula. Por tanto, se debe de cumplir que
vc=ω·R
Representamos las velocidad de traslación del c.m. y la velocidad de rotación en varios puntos del borde de la rueda. Observamos que la velocidad del punto P en contacto con el plano horizontal es nula, vP=0, si vc=ωR
R=1; %radio
v=0.5; %velocidad
hold on
fplot(@(t) R*cos(t), @(t) R*sin(t), [0, 2*pi])
for th=0:pi/6:2*pi
quiver(R*cos(th), R*sin(th),v,0, 'color','b')
quiver(R*cos(th), R*sin(th), v*sin(th), -v*cos(th), 'color','r')
end
quiver(0,0,v,0, 'color','b')
hold off
axis equal
grid on
axis off
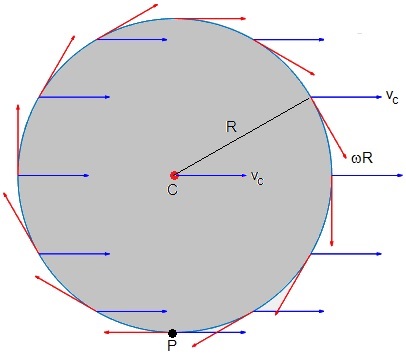
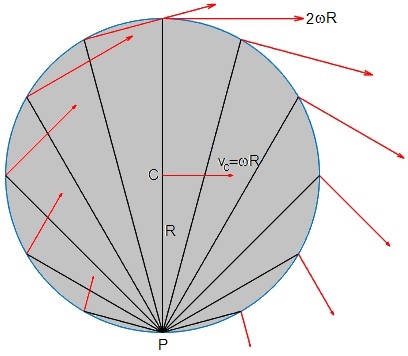
Representamos la suma vectorial de las dos velocidades, en varios puntos del borde de la rueda. Observamos que por el punto P pasa el eje instantáneo de rotación.
R=1; %radio
v=0.5; %velocidad
hold on
fplot(@(t) R*cos(t), @(t) R*sin(t), [0, 2*pi])
for th=0:pi/6:2*pi
quiver(R*cos(th), R*sin(th),v+ v*sin(th),-v*cos(th), 'color','r')
line([0,R*cos(th)],[-R,R*sin(th)], 'color','k')
end
quiver(0,0,v,0, 'color','r')
hold off
axis equal
grid on
axis off
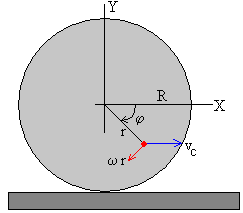
Calculamos la velocidad de cualquier punto P, que dista r del centro de una rueda de radio R y que forma un ángulo φ, con la horizontal. Los ángulos se miden en sentido de las agujas del reloj, que es el sentido del movimiento de rotación de la rueda.
El módulo y el ángulo que forman con el eje horizontal X son, respectivamente
Ejemplo:
Sea r=R=1;
- Cuando φ=π/2, v=0
- Cuando φ=π, , θ=π/4
- Cuando φ=3π/2, v=2vc, θ=0
Sea r=0.5
- Cuando φ=π/2, v=0.25, θ=0
- Cuando φ=π, , θ=0.46 rad=26.6º
- Cuando φ=3π/2, v=1.5vc, θ=0
Composición de movimientos
En este programa interactivo se trata de comprobar que el movimiento general de un sólido rígido es la composición de un movimiento de traslación del centro de masas y de un movimiento de rotación alrededor de un eje que pasa por el centro de masas.
Por otra parte, se trata de establecer la relación que debe de existir entre las velocidades de traslación y de rotación para producir un movimiento de rodar sin deslizar.
Se introduce:
- La velocidad angular de rotación, en el control titulado v. rotación
- La velocidad de traslación del centro de masas se ha fijado en vc=1.0
- El radio de la rueda, se ha fijado en R=1.0
Se pulsa el botón titulado Nuevo
Se representa el perfil de velocidades de diversos puntos de la rueda y en particular, los situados en su diámetro vertical, que son los más importantes para la resolución de los problemas. Observamos, que las velocidades de dichos puntos (en color rojo en la figura de abajo) son la suma vectorial de su velocidad de traslación (en color azul en la figura intermedia) y de su velocidad de rotación (en color azul en la figura de arriba).
En el movimiento de rodar sin deslizar, la velocidad del punto de la rueda que está en contacto con el plano horizontal debe de ser cero. Por tanto, la relación entre las velocidades angular de rotación ω y traslación vc deberá ser vc=ω·R. Observar que:
- La velocidad del punto de la rueda que está en contacto con el plano horizontal debe de ser cero
- La velocidad del centro de masas es vc
- La velocidad del punto más alto de la rueda es el doble de la velocidad del centro de masas, 2·vc
Velocidad y trayectoria de un punto de una rueda.
Consideremos un disco de radio R, que tiene una hendidura de radio r<R que rueda a lo largo del eje X. La velocidad constante de traslación del centro del disco es vc y la velocidad angular de rotación alrededor de un eje perpendicular al disco y que pasa por su centro es ω. Si el disco rueda sin deslizar vc=ωr
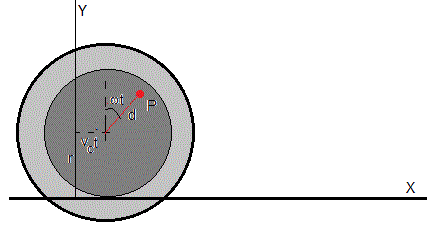
La posición de un punto P de la rueda distante d del eje respecto a los ejes fijos X, Y en el instante t es
x=vct+dsin(ωt)
y=r+dcos(ωt)
R=1; %Radio de la rueda
r=0.75; %radio
V=1; %velocidad de traslación
w=V/r; %velocidad angular de rotación
hold on
line([-1,11],[0,0],'lineWidth',1.5','color','k')
th=0:pi/180:2*pi;
plot(R*cos(th),r+R*sin(th),'k')
plot(r*cos(th),r+r*sin(th),'k')
for d=1:-0.25:0.25
fplot(@(t) V*t+d*sin(w*t), @(t) r+d*cos(w*t),[0,10])
end
hold off
axis equal
axis off

En el programa interactivo, observamos el vector velocidad y la trayectoria que describe un punto de la rueda.
- Cambiamos la posición del punto de color azul sobre el diámetro de la rueda en el control titulado Distancia
En la parte superior, observamos la posición del punto relativa al centro de la rueda cuyo radio está fijado por el programa interactivo y es de un metro
Se introduce:
- La velocidad angular de rotación, en el control titulado v. rotación
- La velocidad de traslación del centro de masas se ha fijado en vc=1.0
- El radio de la rueda, se ha fijado en R=1.0
Se pulsa el botón titulado Nuevo.
Observamos la trayectoria de un punto de la rueda y su vector velocidad, tangente a la trayectoria. El vector velocidad de un punto de la rueda es la suma de
- El vector velocidad en el movimiento de traslación, que es constante.
- El vector velocidad en el movimiento de rotación cuyo módulo es constante pero cuya dirección va cambiando, es perpendicular a la dirección radial y su longitud es proporcional a la distancia entre el punto de la rueda y el centro de la misma.
Se considerará aquellas situaciones en las que el disco rueda sin deslizar, (cuando la velocidad de rotación y de traslación coinciden: 1 rad/s y 1 m/s, respectivamente, ya que el radio es de un metro). Se observará, en esta situación, el movimiento de:
- Un punto que está en la periferia de la rueda
- El centro de la rueda
- Un punto situado entre el centro y la periferia.

