Flexión de una regla.
Supongamos una regla de anchura b, espesor c y longitud L, hecha de un material cuyo módulo de Young es Y.
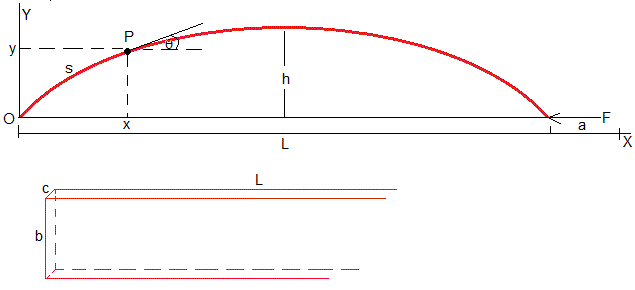
Situamos la regla, sobre una mesa, apoyada sobre su cara más pequeña. Su dirección es el eje X.
La figura muestra la regla doblada simétricamente. El extremo izquierdo se mantiene en el origen y el extremo derecho se desplaza una longitud a, su nueva posición es (L-a,0) cuando se aplica una fuerza F. El punto medio de la regla se desplaza h a lo largo del eje Y
Al punto P de coordenadas (x,y) le corresponde un arco de longitud s. La tangente a la regla en el punto P forma un ángulo θ con la horizontal
Supondremos que la sección de la regla no cambia cuando se dobla
La ecuación diferencial
Aplicamos la ecuación de Euler-Bernoulli que relaciona el momento flector M de la fuerza aplicada y el radio de curvatura ρ de la regla deformada
donde Y es el módulo de Young del material e I es el momento de inercia de la sección transversal respecto del eje neutro, I=bc3/12
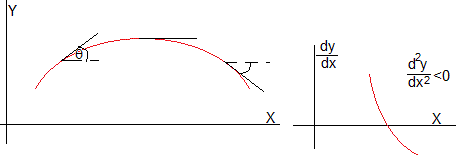
Para una curva cóncava, la pendiente dy/dx=tanθ decrece, la derivada segunda es negativa, por lo que el radio de curvatura ρ=-ds/dθ
Como el momento de las fuerzas respecto del punto P es M=F·y, la ecuación M=YI/ρ, se escribe
Derivando con respecto de s
Se trata de una ecuación diferencial similar a la de un péndulo, para cualquier amplitud. Seguiremos un procedimiento similar para resolverla
En el origen, (0,0), s=0, la tangente a la regla forma el ángulo θ0 que no conocemos, el momento M de las fuerzas respecto a este punto y=0 es cero, por lo que las condiciones iniciales son
En el extremo derecho, (L-a,0), s=L, por simetría, se cumple que
Como no conocemos las condiciones iniciales en el origen, completamente. Tendríamos que resolver la ecuación diferencial por procedimientos numéricos probando valores del ángulo θ0 hasta que se cumplan las condiciones en el extremo derecho de la regla. Sin embargo, como hemos visto con el péndulo hay una solución analítica para esta ecuación diferencial en términos de las funciones elípticas de Jacobi
Solución de la ecuación diferencial
Definimos la variable adimensional, τ
La ecuación diferencial se escribe
Llamando w=dθ/dτ,
la ecuación diferencial se convierte en
Integramos con respecto a θ, teniendo en cuenta la condición inicial: que el ángulo inicial es θ0 y dθ/ds=0 ó w=dθ/dτ=0
Integramos
Hacemos el cambio de variable
El resultado es
donde hemos llamado k a
En términos de la función elípticas de Jacobi, sn
sn es una función elíptica de Jacobi y K es la integral elíptica completa de primera especie
Representamos gráficamente las funciones sn y cn
k=0.3;
x=linspace(0,8,200);
hold on
[sn,cn,dn]=ellipj(x,k^2);
plot(x,sn)
plot(x,cn)
K=ellipke(k^2);
line([0,2*K],[0,0],'lineWidth',1.5, 'color','r')
line([2*K,4*K],[0,0],'lineWidth',1.5, 'color','b')
line([2*K,2*K],[0,-1],'lineStyle','--')
line([4*K,4*K],[0,1],'lineStyle','--')
hold off
xlabel('x')
ylabel('sn(x), cn(x)')
legend ('sn','cn', 'location', 'southwest')
title('Funciones elípticas de Jacobi')
grid on
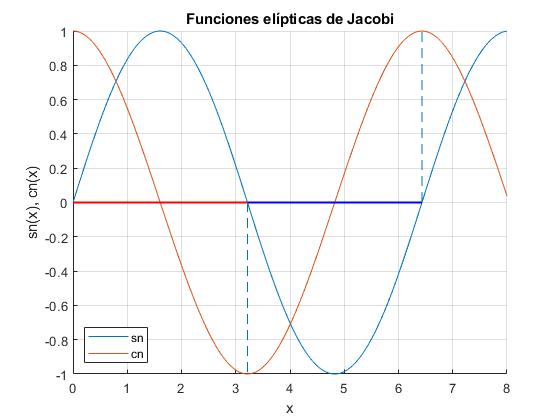
Se trata de dos funciones periódicas de periodo 4K, siendo K la integral elíptica completa de primera especie. El segmento de color rojo o de color azul mide 2K
La suma de los cuadrados es la unidad, sn2+cn2=1. Por ejemplo, para k=0.3 y x=2
>> [sn,cn,dn]=ellipj(2,k^2); >> sn^2+cn^2 ans = 1
Sea τ0 el valor de τ correspondiente a s=L (extremo derecho de la barra)
Se cumple que
Para calcular k o el ángulo θ0, resolvemos la ecuación transcendente τ0/2-K=0. Gráficamente
tau_0=5;
hold on
fplot(@(x) ellipke(x.^2),[0,1])
line([0,1],[tau_0/2,tau_0/2], 'color','r')
f=@(x) tau_0/2-ellipke(x^2);
k=fzero(f,[0,0.99999]);
plot(k,ellipke(k^2),'o','markersize',4,'markeredgecolor','k','markerfacecolor','k')
line([k,k],[1.5,ellipke(k^2)],'lineStyle','--')
hold off
grid on
xlabel('x')
ylabel('y')
title('Elíptica completa')
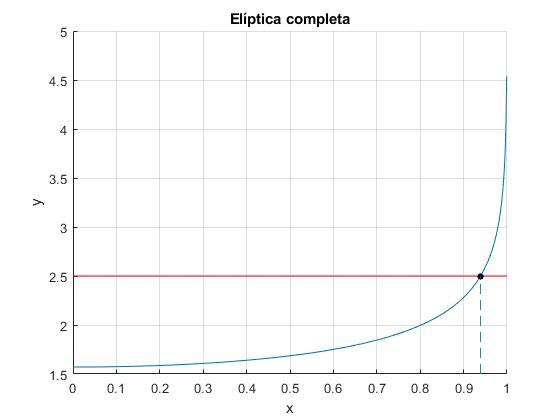
Obtenemos el valor de k para τ0=5
>> k k = 0.9391
Como el valor mínimo de la integral elíptica completa es K(0)=1.5708. El valor mínimo de τ0=2K(0). La fuerza mínima necesaria para doblar la regla es
Para una regla de L=2 m de longitud, anchura b=17.3 mm, espesor c=2.4 mm y módulo de Young Y=12·1012 N/m2
>> F=Y*I*(2*ellipke(0)/L)^2 F = 590.0918
Si la fuerzas F que aplicamos a los extremos son inferiores a Fm=590 N, la regla no se dobla
Conocido el valor de k, obtenemos la pendiente θ de la recta tangente a la curva que describe la regla doblada en el intervalo 0≤τ≤τ0 o bien, 0≤s≤L
Conocido el ángulo θ en función de τ o de , se calculan las coordenadas x e y de los puntos de dicha curva
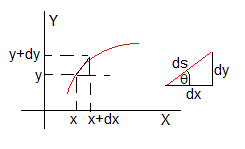
Evaluamos estas dos integrales numéricamente utilizando la función
Tenemos otra forma de calcular la ordenada y de los puntos de la curva. Partimos de la ecuación diferencial
Se ha utilizado la propiedad, sn2+cn2=1
El máximo de y se produce para s=L/2, o bien para τ=τ0/2=K
Esta es la relación entre el máximo desplazamiento de la regla doblada h y la fuerza aplicada F.
La relación entre las variables s y τ, nos proporciona otra relación interesante
Multiplicando miembro a miembro ambas relaciones
Ejemplo
Sea una regla de L=2 m de longitud, anchura b=17.3 mm, espesor c=2.4 mm y módulo de Young Y=12·1012 N/m2
Se aplica la fuerza F=770 N, mayor que valor mínimo Fm=590 N
Los pasos son:
- Calculamos k resolviendo la ecuación transcendente, τ0/2-K=0
- Calculamos el ángulo θ en función de τ o s
- Calculamos las coordenadas (x,y) de la curva que describe la regla doblada y la representamos
L=2; %longitud de regla
Y=12e12; %módulo de Young
b=17.3/1000; %anchura
c=2.4/1000; %espesor
I=b*c^3/12; %momento de inercia
F=770; %fuerza aplicada
tau_0=L*sqrt(F/(Y*I));
f=@(x) tau_0/2-ellipke(x^2);
k=fzero(f,[0,0.99999]);
tau=linspace(0,tau_0,100);
K=ellipke(k^2);
[sn,cn,dn]=ellipj(tau+tau_0/2, k^2);
th=2*asin(k*sn);
s=linspace(0,L,100);
x=zeros(1,length(s));
y=zeros(1,length(s));
x(1)=0; y(1)=0;
for i=2:length(s)
x(i)=trapz(s(1:i),cos(th(1:i)));
y(i)=trapz(s(1:i),sin(th(1:i)));
end
plot(x,y)
axis equal
grid on
xlabel('x')
ylabel('y')
title('Elástica')
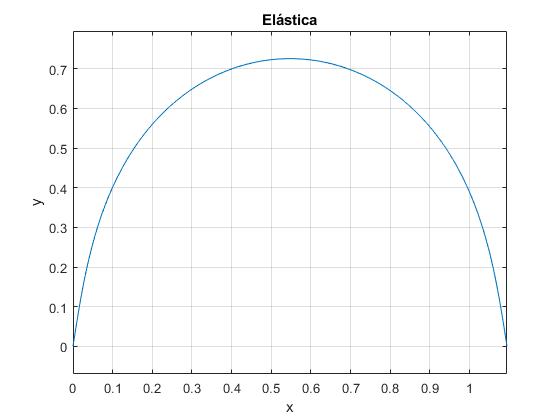
La posición del extremo derecho de la regla es
>> x(end),y(end) ans = 1.0944 ans = 6.1930e-16
El extremo derecho de la regla se ha desplazado horizontalmente a=L-x(L)=2-1.0944=0.9056 m
El máximo desplazamiento h de la regla (en el punto medio) es
>> 2*sqrt(Y*I/F)*k ans = 0.7256
Cambiamos la fuerza F=2800 N
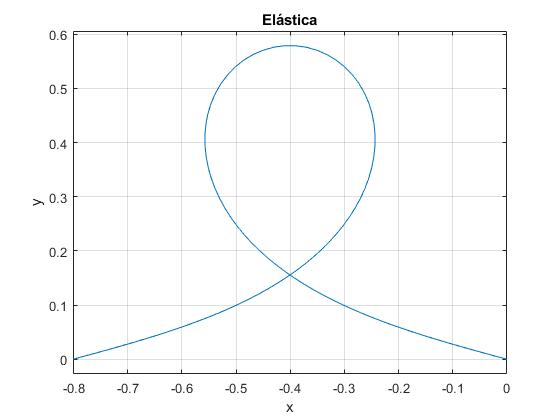
La posición del extremo derecho de la regla es
>> x(end),y(end) ans = -0.8012 ans = 8.1098e-17
El extremo derecho de la regla se ha desplazado horizontalmente a=L-x(L)=2+0.8012=2.8012 m
El desplazamiento h del punto medio de la regla es
>> 2*sqrt(Y*I/F)*k ans = 0.5794
Solución analítica para pequeñas deformaciones
Para pequeñas deformaciones, se cumple aproximadamente
La ecuación diferencial de la regla, utilizando estas aproximaciones, se convierte en
La solución de esta ecuación diferencial es
Los extremos de la regla flexionada están en el eje X, uno en el origen y otro en L-a, siendo a el desplazamiento horizontal del extremo derecho de la regla
Por otra parte, el momento de las fuerzas aplicadas en los extremos respecto de la posición de los extremos y=0 es nulo, por lo que dθ/ds=0 en ambos
Las condiciones de contorno conducen a las siguientes resultados:
En el origen, x=0
La condición y(0)=0, conduce a D=0
La condición
En el extremo derecho, x=L-a
La condición
La condición y(L-a)=0
El coeficiente B=0 es nulo
Consideraremos el caso m=1, ω=π/(L-a)
Fuerza F que es necesario aplicar para producir el desplazamiento a del extremo derecho es
El valor mínimo de la fuerza F es
En el caso de que la fuerza aplicada F sea menor que la mínima Fm la regla no se deforma
conduce a C=0
La solución de la ecuación diferencial aproximada es y=Asin(ωx). La amplitud A, o máximo desplazamiento del punto medio de la regla se determina a partir de la longitud L de la regla
La amplitud A es la raíz de esta ecuación transcendente.
Supongamos una regla de L=2 m de longitud. El extremo derecho se ha desplazado, a=0.36 m. Calculamos la amplitud A, resolviendo la integral por procedimiento numéricos, empleando la función
L=2; %longitud de regla a=0.36; %desplazamiento w=pi/(L-a); f=@(A) integral(@(x) sqrt(1+(A*w*cos(w*x)).^2),0,L-a)-L; A=fzero(f,2*sqrt(a*(L-a))/pi)
A = 0.5268
Nueva aproximación
Cuando el segundo término bajo la raíz es pequeño frente a la unidad, utilizamos los dos primeros términos del desarrollo
>> syms x; >> taylor(sqrt(1+x^2)) ans =- x^4/8 + x^2/2 + 1
Teniendo en cuenta el valor de la integral
El resultado es
La forma aproximada de la regla deformada es
Ejemplo
Sea una regla de L=2 m de longitud, anchura b=17.3 mm, espesor c=2.4 mm y módulo de Young Y=12·1012 N/m2
Se somete la regla a la acción de la fuerza F=650 N, un poco mayor que valor mínimo Fm=590 N
- Resolvemos la ecuación diferencial exacta, calculando la posición del extremo derecho L-a
- Con este dato, repesentamos aproximadamente la forma de la regla mediante la función seno, calculando la amplitud A de forma numérica
- Repesentamos aproximadamente la forma de la regla mediante la función seno, utilizando la expresión
L=2; %longitud de regla
Y=12e12; %módulo de Young
b=17.3/1000; %anchura
c=2.4/1000; %espesor
I=b*c^3/12; %momento de inercia
F=650; %fuerza aplicada
tau_0=L*sqrt(F/(Y*I));
f=@(x) tau_0/2-ellipke(x^2);
k=fzero(f,[0,0.99999]);
tau=linspace(0,tau_0,100);
K=ellipke(k^2);
[sn,cn,dn]=ellipj(tau+tau_0/2, k^2);
th=2*asin(k*sn);
s=linspace(0,L,100);
x=zeros(1,length(s));
y=zeros(1,length(s));
x(1)=0; y(1)=0;
for i=2:length(s)
x(i)=trapz(s(1:i),cos(th(1:i)));
y(i)=trapz(s(1:i),sin(th(1:i)));
end
hold on
plot(x,y)
%aproximación
a=L-x(end); %desplazamiento horizontal
w=pi/(L-a);
f=@(A) integral(@(x) sqrt(1+(A*w*cos(w*x)).^2),0,L-a)-L;
A=fzero(f,2*sqrt((L-a)*a)/pi);
fplot(@(x) A*sin(w*x),[0,La])
fplot(@(x) 2*sqrt((L-a)*a)*sin(w*x)/pi,[0,L-a])
hold off
legend('exacta','seno','seno aprox.','location','best')
axis equal
grid on
xlabel('x')
ylabel('y')
title('Elástica')
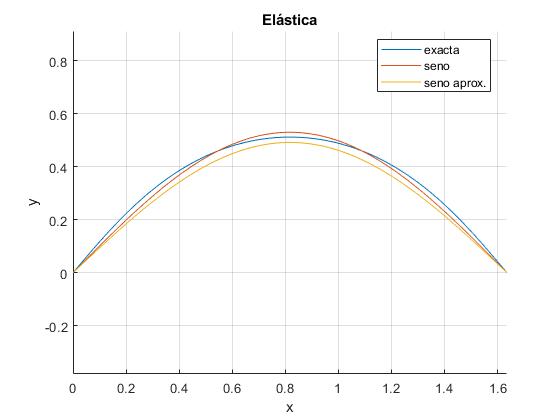
En la descripción aproximada, la fuerza F que tenemos que aplicar para producir un desplazamiento a del extremo derecho, es mayor que la mínima Fm
>> a a = 0.3643 >> F=Y*I*(pi/(L-a)^2 F = 882.2305 >> Fm=Y*I*(pi/L)^2 Fm = 590.0918
Calculamos el desplazamiento h del punto medio de la regla, en el caso exacto y aproximado
2*sqrt(Y*I/F)*k ans = 0.5116 >> A A = 0.5298 >> 2*sqrt(a*(L-a))/pi ans = 0.4914
Incrementamos un poco más la fuerza F=700 N. Observamos que la solución aproximada, difiere sustancialmente de la calculada a partir de la ecuación diferencial exacta.
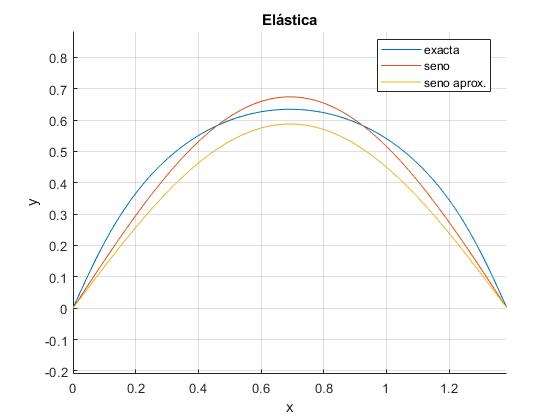
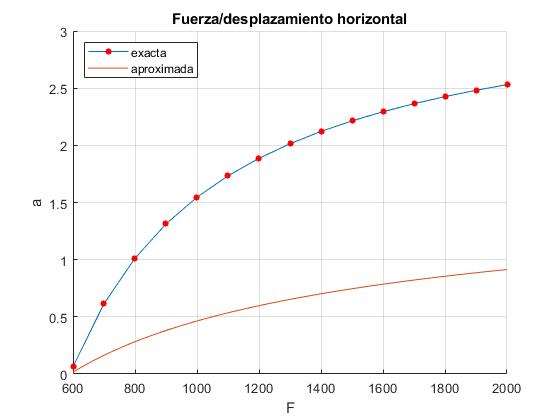
Desplazamiento horizontal del extremo de la regla
Representamos el desplazamiento horizontal a del extremo derecho de la regla en función de la fuerza F>Fm
Para el caso exacto, la relación es
-
Para el caso aproximado,
L=2; %longitud de regla
Y=12e12; %módulo de Young
b=17.3/1000; %anchura
c=2.4/1000; %espesor
I=b*c^3/12; %momento de inercia
hold on
FF=600:100:2000;
a=zeros(1,length(FF));
j=1;
for F=FF %fuerza aplicada
tau_0=L*sqrt(F/(Y*I));
f=@(x) tau_0/2-ellipke(x^2);
k=fzero(f,[0,0.99999]);
tau=linspace(0,tau_0,100);
K=ellipke(k^2);
[sn,cn,dn]=ellipj(tau+tau_0/2, k^2);
th=2*asin(k*sn);
s=linspace(0,L,100);
a(j)=L-trapz(s,cos(th));
j=j+1;
end
plot(FF,a,'o-','markersize',4,'markeredgecolor','r','markerfacecolor','r')
%aproximación
desp=@(F) L-pi*sqrt(Y*I./F);
fplot(desp,[600,2000])
hold off
legend('exacta','aproximada','location','northwest')
grid on
xlabel('F')
ylabel('a')
title('Fuerza/desplazamiento horizontal')
Desplazamiento del punto medio de la regla
Representamos el máximo desplazamiento h (del punto medio de la regla) en función de la fuerza F
Para el caso exacto, la relación es
-
Para el caso aproximado, es la amplitud A, raíz de la ecuación transcendente o bien, su expresión analítica aproximada
L=2; %longitud de regla
Y=12e12; %módulo de Young
b=17.3/1000; %anchura
c=2.4/1000; %espesor
I=b*c^3/12; %momento de inercia
hold on
FF=600:100:2000;
h=zeros(1,length(FF));
A0=zeros(1,length(FF));
j=1;
for F=FF %fuerza aplicada
tau_0=L*sqrt(F/(Y*I));
f=@(x) tau_0/2-ellipke(x^2);
k=fzero(f,[0,0.99999]);
h(j)=2*sqrt(Y*I/F)*k;
%aproximado
w=sqrt(F/(Y*I));
a=L-pi/w;
f=@(A) integral(@(x) sqrt(1+(A*w*cos(w*x)).^2),0,L-a)-L;
A0(j)=fzero(f,2*sqrt((L-a)*a)/pi);
j=j+1;
end
plot(FF,h,'o-','markersize',4,'markeredgecolor','r','markerfacecolor','r')
plot(FF,A0,'o-','markersize',4,'markeredgecolor','b','markerfacecolor','b')
%aproximación
amp=@(F) 2*sqrt((L-pi*sqrt(Y*I./F))*pi.*sqrt(Y*I./F))/pi;
fplot(amp,[600,2000])
hold off
legend('exacta','numérica aprox.','aprox.','location','south')
grid on
xlabel('F')
ylabel('h')
title('Fuerza/desplazamiento vertical')
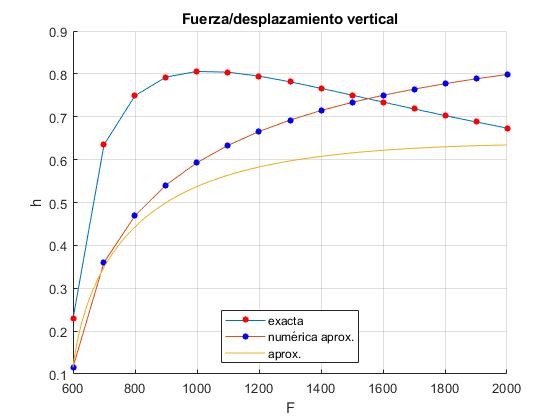
El máximo desplazamiento h, primero crece y luego, decrece, alcanzando un máximo, en esto difiere de la descripción aproximada
Experiencia
Tomamos una regla de plástico que mide hasta 30 cm, cuya longitud es L=31.2 cm, la doblamos empujando con los dedos de la mano. Situamos un extremo en el origen y el otro extremo lo desplazamos a=3.2 cm hasta la medida 28 cm. Dibujamos la forma de la regla deformada sobre un papel, midiendo con la regla las coordenadas de los puntos (x,y) tal como se muestra en la figura
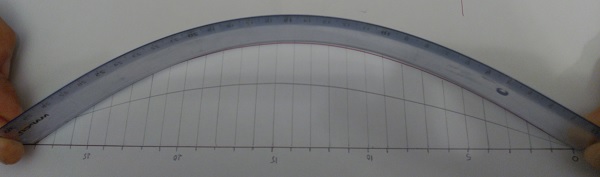
| x (cm) | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| y (cm) | 0 | 0.7 | 1.4 | 2.0 | 2.6 | 3.2 | 3.7 | 4.2 | 4.9 | 4.5 | 5.1 | 5.4 | 5.6 | 5.7 | 5.8 | 5.8 | 5.7 | 5.6 | 5.4 | 5.2 |
| x (cm) | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 |
|---|---|---|---|---|---|---|---|---|---|
| y (cm) | 4.8 | 4.5 | 4.1 | 3.5 | 3.0 | 2.3 | 1.7 | 0.9 | 0 |
Para pequeñas deformaciones de la regla, la función que describe la forma que adopta es
Con los datos del desplazamiento horizontal a=3.2 cm y la longitud de la regla L=31.2 cm, obtenemos, y=6.02·sin(0.11·x)
Representamos los datos experimentales de la tabla y los ajustamos a la función no lineal y=Asin(ωx) utilizando la función
L=31.2; %longitud
a=3.2; %desplazamiento horizontal
A=2*sqrt(a*(L-a))/pi; %amplitud
w=pi/(L-a); %frecuencia angular
%datos experimentales
x=0:28;
y=[0,0.7,1.4,2.0,2.6,3.2,3.7,4.2,4.5,4.9,5.1,5.4,5.6,5.7,5.8,5.8,5.7,
5.6,5.4,5.2,4.8,4.5,4.1,3.5,3.0,2.3,1.7,0.9,0];
%ajuste
hold on
plot(x,y,'ro','markersize',4,'markerfacecolor','r')
f=@(a,x) a(1)*sin(a(2)*x);
a0=[A,w]; %valor inicial
af=nlinfit(x,y,f,a0);
g=@(x) f(af,x);
fplot(g,[x(1),x(end)])
hold off
axis equal
grid on
xlabel('x')
ylabel('y')
title('Ajuste no lineal, y=a·sin(bx)')
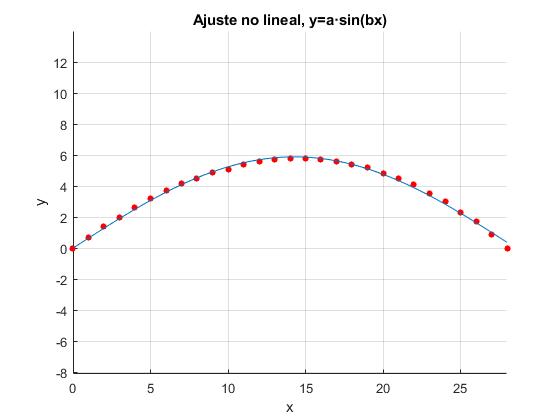
>>af af = 5.8877 0.1099
Obtenemos A=5.89 y ω=0.11, que son próximos a los valores calculados anteriormente mediante la aproximación de pequeñas deformaciones
Referencias
Anders Johansson. The curve shape of a bent ruler, -analytical, numerical and experimental studies. Phys. Educ. 54 (2019) 035018
M. E. Pacheco Q., E. Piña. The elastic rod. Revista Mexicana de Física. E 53 (2) 186-190, Diciembre 2007

