La catenaria
Consideremos un cable de longitud L sujeto por sus dos extremos que están situados a la misma altura y que distan 2a uno del otro. Sea λ la densidad del cable (masa por unidad de longitud).
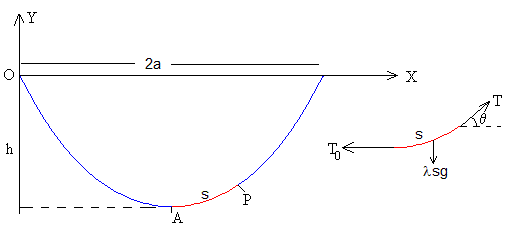
En la figura, se representa las fuerzas que actúan sobre una porción s de cable que tiene como extremo el punto más bajo A:
- el peso, λgs, producto de la densidad lineal, por la gravedad, por la longitud de la cuerda
- la fuerza T0, que ejerce la parte izquierda del cable sobre el extremo izquierdo A de dicho segmento
- la fuerza T, que ejerce la parte derecha del cable sobre el extremo derecho P .
La condición de equilibrio se escribe
Tcosθ=T0
Tsinθ=λgs
O bien,
Derivando con respecto de x, y teniendo en cuenta que la longitud del arco diferencial ds2=dx2+dy2
Integrando esta ecuación, teniendo en cuenta que para x=a, v=dy/dx=0.
Integrando de nuevo, con la condición de que para x=a, y=-h.
Como la catenaria es simétrica para x=2a, y=0, por lo que la flecha h vale.
La ecuación de la catenaria es, finalmente
La longitud de la catenaria es
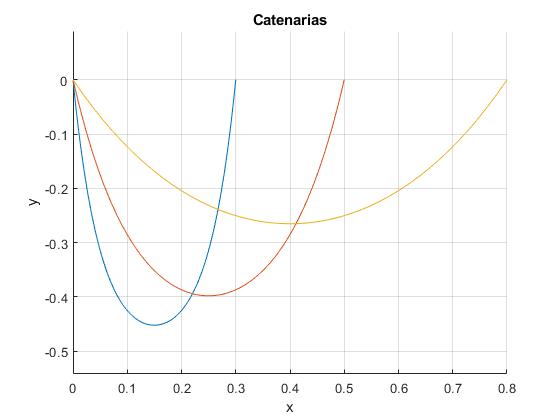
Para dibujar una catenaria simétrica de longitud L, cuya "luz" es a
- Se resuelve la ecuación transcendente, calculando el valor de γ
- Se representa la catenaria
- Se calcula el mínimo o la "flecha" h
L=1; %longitud de las catenarias
hold on
for a=[0.3,0.5,0.8]/2 %luz 2a de las catenarias
f=@(x) sinh(a*x)-L*x/2;
gamma=fzero(f,[0.1 100]);
f=@(x) (cosh(gamma*(x-a))-cosh(gamma*a))/gamma;
fplot(f,[0,2*a]);
end
hold off
axis equal
grid on
xlabel('x');
ylabel('y');
title('Catenarias')
Tensión del cable
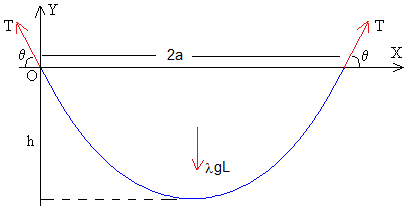
En la figura se muestran las fuerzas sobre el cable de longitud L, densidad λ y cuyos extremos están a la misma altura separados una distancia a
El peso, λgL, aplicado en un punto situado en el eje de simetría
La fuerza T que ejercen los postes sobre los extremos del cable, que forman un ángulo θ con la horizontal
La componente horizontal de la fuerza Tcosθ=T0 es constante en todos los puntos de la catenaria. La componente vertical, por simetría, es la mitad del peso del cable
Donde hemos definido las tensiones adimensionales τ=T/(λga) y τ0=T0/(λga) y la longitud adimensional L/a del cable
En la ecuación transcendente, fijado a, calculamos τ0
Elaboramos un script para calcular la componente horizontal τ0 de la tensión y a continuación, la tensión τ del cable en su extremo, en función de la longitud del cable L/(2a)
longitud=1.05:0.05:3;
%la luz 2a=1
tension=zeros(1,length(longitud));
i=1;
for l=longitud
f=@(x) sinh(1/x)-l/x;
T0=fzero(f,1);
tension(i)=sqrt(T0^2+l^2);
i=i+1;
end
plot(longitud,tension)
grid on
xlabel('L/(2a)')
ylabel('T/(\lambdaga)')
title('Catenaria')
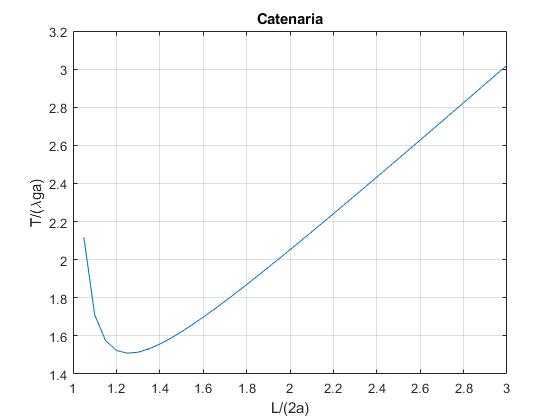
Buscamos el mínimo de la tensión y la longitud del cable L/a correspondiente a este mínimo
>> [M,I]=min(tension) M = 1.5091 I = 5 >> longitud(I) ans = 1.2500
La longitud óptima de un cable cuyos extremos cuelgan de postes de la misma altura separados una distancia 2a es L=1.25·2a
El mínimo se encuentra en el intervalo (1.2,1.3). Elaboramos otro script similar para localizar el mínimo con mayor precisión
longitud=1.2:0.001:1.3; %la luz 2a=1 tension=zeros(1,length(longitud)); i=1; for l=longitud f=@(x) sinh(1/x)-l/x; T0=fzero(f,1); tension(i)=sqrt(T0^2+l^2); i=i+1; end [M,I]=min(tension); disp(longitud(I))
1.2580
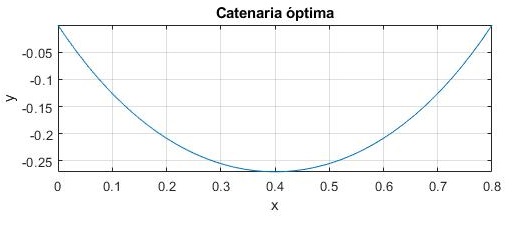
Dibujamos la catenaria óptima cuyos extremos distan 2a=0.8
a=0.4; %'luz' 2a
L=1.2580*2*a;%longitud de las catenaria
f=@(x) sinh(a*x)-L*x/2;
gamma=fzero(f,[0.1 100]);
f=@(x) (cosh(gamma*(x-a))-cosh(gamma*a))/gamma;
fplot(f,[0,2*a]);
axis equal
grid on
xlabel('x');
ylabel('y');
title('Catenaria óptima')
Energía potencial mínima
Consideremos un cable flexible, de longitud L que cuelga de los puntos (-a,h) y (a,h) tal como se muestra en la figura.
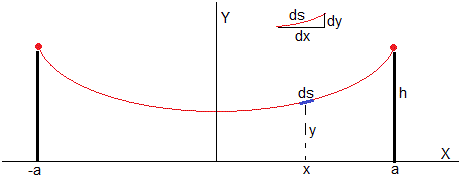
La longitud L del cable es
El cable está en una configuración de equilibrio estable, lo que significa que su energía potencial es mínima. La energía potencial de una porción de cable de densidad uniforme λ y de longitud ds es (λ·ds)gy, siendo y la altura del cable sobre el eje X.
Un problema similar isoperimétrico estudiado en la página titulada 'Cálculo de variaciones'. Formamos la función F dependiente de un parámetro k
Aplicando la ecuación de Euler-Lagrange a la función F que no depende de x
Llamando z=(λgy+k)/C1, dz=λg·dy/C1
Haciendo el cambio z=coshu, dz=sinhu·du
Llamando γ=λga/C1, tenemos una ecuación más simple
Aplicamos las condiciones de contorno para determinar las constantes γ y C2. Para x1=-a, y1=h y para para x2=a, y2=h. Por simetría C2=0
La constante γ se calcula sabiendo que la longitud de la catenaria es L
Resolvemos la ecuación trascendente para calcular γ
Sabiendo que para x=a, y=h, obtenemos el parámetro k/(λg)
Finalmente, la ecuación de la catenaria es
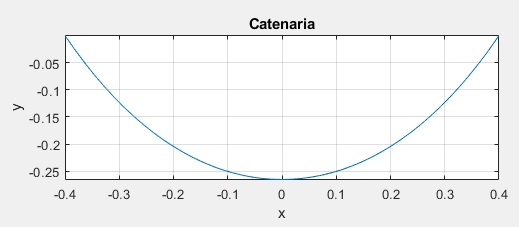
Conocidos la longitud L de la catenaria y la 'luz' 2a, se resuelve la ecuación trascendente para calcular γ. Conocido h que puede ser cero, se representa la catenaria
L=1; %longitud de las catenarias
h=0; %altura
a=0.4;
f=@(x) sinh(x)/x-L/(2*a);
gamma=fzero(f,[0.1 100]);
f=@(x) a*(cosh(gamma*x/a)-cosh(gamma))/gamma+h;
fplot(f,[-a,a])
axis equal
grid on
xlabel('x');
ylabel('y');
title('Catenaria')
Catenaria asimétrica
Partimos de la ecuación de la catenaria
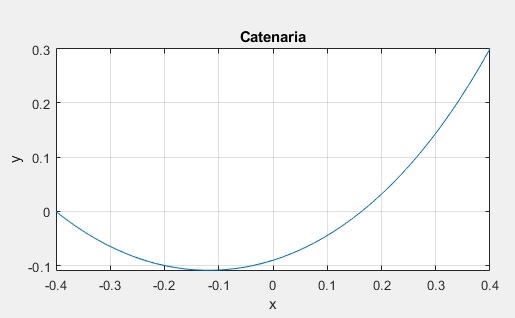
Sea una catenaria asimétrica que cuelga de dos puntos (-a, 0) y (a, h)
(1)
Restando las ecuaciones (1), eliminamos el parámetro k desconocido
Se ha utilizado la relación
>> syms A B; >> expand(cosh(A+B)-cosh(-A+B)) ans =2*sinh(A)*sinh(B)
El parámetro k se calcula sabiendo que la longitud de la catenaria es L
Se ha utilizado la relación
>> expand(sinh(A+B)-sinh(-A+B)) ans =2*cosh(B)*sinh(A)
Dividiendo estas dos relaciones se obtiene
Se despeja C2 y luego, γ, empleando cualesquiera de las dos relaciones anteriores, la correspondiente a la longitud L o a la altura h
Sumando las ecuaciones (1)
La ecuación de la catenaria se escribe en términos de los parámetros conocidos C2 y γ
Dados los datos de la longitud de la cadena flexible L, la distancia 2a entre los puntos fijos y la altura h
- Calculamos C2 a partir de h y L
- Resolvemos la ecuación trascendente y obtenemos la raíz, γ
- Dibujamos la curva catenaria entre los puntos (-a,0) y (a,h)
L=1; %longitud de las catenaria
h=0.3; %altura
a=0.4; %2a es la 'luz'
C2=atanh(h/L);
f=@(x) sinh(x)-x*L/(2*a*cosh(C2));
gamma=fzero(f,[0.1 100]);
f=@(x) h/2+a*(cosh(gamma*x/a+C2)-cosh(gamma)*cosh(C2))/gamma;
fplot(f,[-a,a])
axis equal
grid on
xlabel('x');
ylabel('y');
title('Catenaria')
La catenaria de longitud no especificada
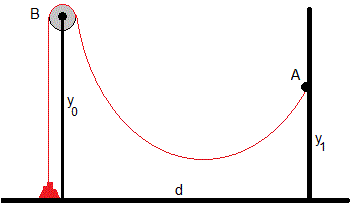
En este apartado, estudiamos la forma que adopta un cable flexible apilado sobre una mesa, tiramos hacia arriba de un extremo, lo pasamos por una polea B situada a una altura y0 y después lo sujetamos a una altura y1 en un poste A situado a una distancia d.
El cable que une los puntos A y B tiene una longitud L desconocida y adoptará una forma tal que su energía potencial sea mínima
En el apartado anterior, calculamos la expresión de la energía potencial de un cable sujetado por sus extremos
El funcional tiene la forma
Aplicando la ecuación de Euler-Lagrange a una función F que no depende de x
Integramos, haciendo el cambio de variable coshu=y/c1
Las constantes c1 y c2 se determinan sabiendo que para x=0, y=y0 y para x=d, y=y1
Llamamos k1=c1 y k2=-c2/c1
Representamos la función f(k2) para y0=1 y d=1
y0=1; %altura izquierda
d=1; %distancia
f=@(x) y0*cosh(d*cosh(x)/y0+x)./cosh(x); %función
fplot(f,[-2.5,1])
g=@(x) (sinh(cosh(x)+x).*(1+sinh(x)).*cosh(x)-cosh(cosh(x)+x).
*sinh(x))./cosh(x).^2; %derivada
k2=fzero(g,-1.5);
line([k2,k2],[0,f(k2)],'lineStyle','--','color','k')
line([-2.5,k2],[f(k2),f(k2)],'lineStyle','--','color','k')
ylim([0,4])
grid on
xlabel('k_2')
ylabel ('y_1')
title('Catenaria')
Para calcular el mínimo de la función y=f(x), derivamos dy/dx=0, e igualamos a cero. La función
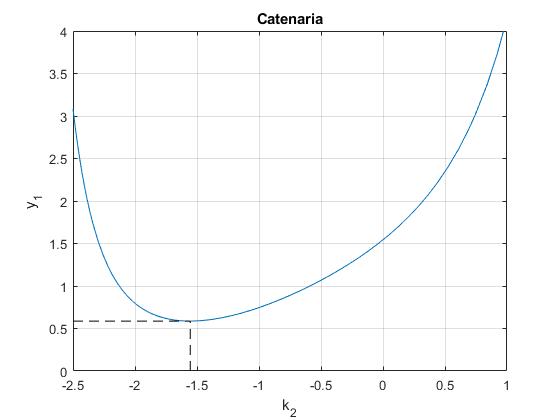
>> k2,f(k2) k2 = -1.5549 ans = 0.5871
Observamos que la función tiene un mínimo para k2=-1.56 que vale y1=0.5871
- Si y1<0.5871, no hay catenaria
- Si y1=0.5871, hay una catenaria
- Si y1>0.5871, hay dos catenarias
Sea y1=0.8, mayor que el valor crítico. Resolvemos la ecuación transcendente y1=f(x) en las proximidades de x=-2 y de x=0.5 empleando la función
y0=1; %altura izquierda
d=1; %distancia
y1=0.8; %altura derecha >0.59
f=@(x) y0*cosh(d*cosh(x)/y0+x)./cosh(x)-y1;
hold on
for k2=[fzero(f,-2),fzero(f,0.5)]
k1=y0/cosh(k2);
fplot(@(x) k1*cosh(x/k1+k2),[0,d]);
end
hold off
grid on
axis equal
xlabel('x')
ylabel ('y')
title('Catenaria')
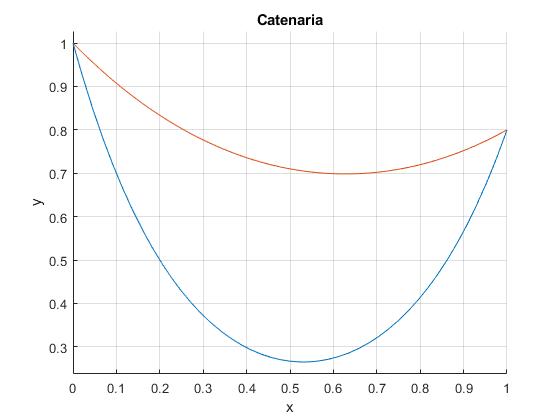
Solamente, una de las dos catenarias es posible
La longitud de la catenaria es
Representamos la función f(k2) para y0=1 y d=1
f=@(x) (sinh(cosh(x)+x)-sinh(x))./cosh(x); %función
fplot(f,[-2.5,1])
g=@(x) (cosh(cosh(x)+x).*(1+sinh(x)).*cosh(x)-sinh(cosh(x)+x)
.*sinh(x)-1)./cosh(x).^2; %derivada
k2=fzero(g,-0.5);
line([k2,k2],[0,f(k2)],'lineStyle','--','color','k')
line([-2.5,k2],[f(k2),f(k2)],'lineStyle','--','color','k')
y1=cosh(cosh(k2)+k2)/cosh(k2);
ylim([0,4])
grid on
xlabel('k_2')
ylabel ('L')
title('Catenaria')
Para calcular el mínimo de la función y=f(x), derivamos dy/dx=0, e igualamos a cero. La función
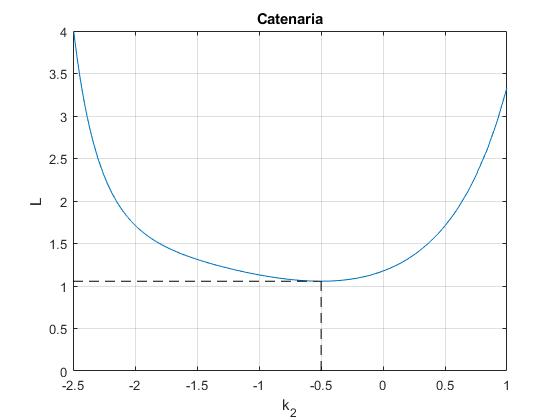
>> k2,f(k2) k2 = -0.4988 ans = 1.0560
La longitud mínima de la catenaria es L=1.0560, que se produce para k2=-0.4988
y0=1; %altura izquierda
d=1; %distancia
k2=-0.4988;
k1=y0/cosh(k2);
fplot(@(x) k1*cosh(x/k1+k2),[0,d]);
axis equal
grid on
xlabel('x')
ylabel ('y')
title('Catenaria')
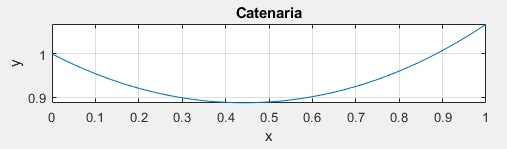
La altura del extremo derecho es y1=1.0682
>> y1=k1*cosh(d/k1+k2) y1 = 1.0682
La catenaria discreta
En este apartado, describimos la forma de una cadena formada por 2N+1 eslabones de longitud d. Cuando el número de eslabones es grande comprobaremos que la forma de la cadena se aproxima a una catenaria.
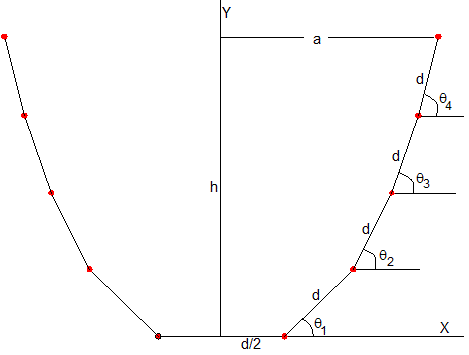
La cadena estará formada por un número impar 2N+1 de eslabones de masa m cada uno, de modo que el central es horizontal y los otros son simétricos respecto del eje vertical Y, tal como se muestra en la figura para una cadena de 9 eslabones.
Estudiamos el equilibrio del primer eslabón y del eslabón k
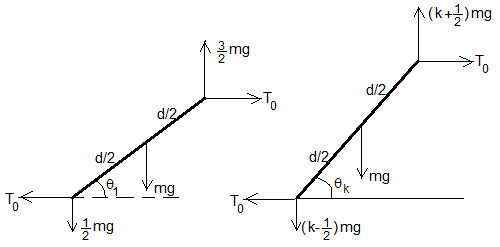
Como la fuerza que actúa sobre la cadena, el peso, es vertical, la componente horizontal T0 es constante en todos los eslabones. Las componentes verticales se identifican fácilmente.
Sobre el extremo izquierdo del primer eslabón actúa hacia abajo la mitad del peso del eslabón horizontal, mg/2, que se equilibra con la fuerza vertical 3mg/2 en el extremo derecho y el peso mg de dicho eslabón.
Sobre el extremo izquierdo del segundo eslabón actuará hacia abajo 3mg/2 (principio de acción y reacción), que se equilibra con la fuerza hacia arriba 5mg/2 en el extremo derecho y el peso mg de dicho eslabón.
En el eslabón k, la fuerza (k-1/2)mg en el extremo izquierdo, representa el peso de medio eslabón horizontal y el peso de los (k-1) eslabones que hay por debajo. Tendremos que ejercer una fuerza hacia arriba (k+1/2)mg en el extremo derecho para equilibrar esa fuerza con el peso de dicho eslabón k.
En el equilibrio, el momento de las fuerzas que actúan sobre el primer eslabón es cero, respecto de cualquier punto, por ejemplo, el extremo izquierdo
En el equilibrio, el momento de las fuerzas que actúan sobre el eslabón k, respecto de cualquier punto, por ejemplo, el extremo izquierdo
La 'flecha' h es
La 'luz' 2a es
Dado el número de eslabones 2N+1, su longitud d y la 'luz' a, resolvemos la ecuación transcendente
para calcular θ1, y las posiciones de las puntos de unión de dos eslabones contiguos (color rojo) y sus simétricos
De la descripción discreta a la continua
Partimos de la relación entre el primer ángulo θ1 que forma el eslabón con la horizontal y el del eslabón k, θk
Derivando con respecto de x, y teniendo en cuenta que la longitud del arco diferencial ds2=dx2+dy2
La misma ecuación que obtuvimos al principio de la página, que vamos a integrar con otras condiciones iniciales
Integrando esta ecuación, teniendo en cuenta que para x=0, v=dy/dx=0.
Integrando de nuevo, con la condición de que para x=0, y=0.
La longitud de la catenaria es
Para dibujar una catenaria simétrica de longitud L, cuya "luz" es 2a
- Se resuelve la ecuación transcendente, calculando el valor de γ
- Se representa la catenaria
- Se calcula el mínimo o la "flecha" h para x=a
Sea una cadena
- de 9 eslabones, N=4
- la longitud de la cadena, L=5.25
- la longitud de cada eslabón, d=L/(2N+1)
- la 'luz', distancia entre extremos, a=2
Representamos la cadena y la catenaria de longitud L y 'luz' 2a
L=5.25; %longitud
N=4; %9 eslabones
d=L/(2*N+1);
k=1:N;
a=1; %luz 2a=2
f=@(x) sum(1./sqrt(1+(k.^2).*(tan(x).^2)))+1/2-a/d;
ang=fzero(f,[0,89*pi/180]);
hold on
x0=d/2; y0=0;
line([-x0,x0],[0,0],'color','k')
plot(x0,0,'o','markersize',4,'markeredgecolor','r','markerfacecolor','r')
plot(-x0,0,'o','markersize',4,'markeredgecolor','k','markerfacecolor','r')
for k=1:N
th=atan(k*tan(ang));
x1=x0+d*cos(th);
y1=y0+d*sin(th);
line([x0,x1],[y0,y1],'color','k')
line([-x0,-x1],[y0,y1],'color','k')
plot(x1,y1,'o','markersize',4,'markeredgecolor','r','markerfacecolor','r')
plot(-x1,y1,'o','markersize',4,'markeredgecolor','r','markerfacecolor','r')
x0=x1;
y0=y1;
end
%continua
g=@(x) sinh(a*x)-L*x/2;
gamma=fzero(g,[0.1 100]);
fplot(@(x) (cosh(gamma*x)-1)/gamma,[-a,a])
hold off
grid on
xlabel('x')
ylabel('y')
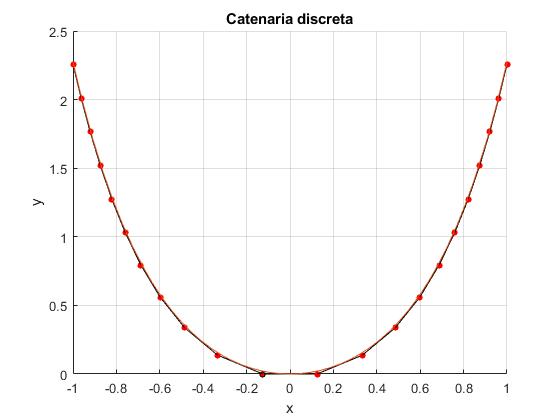
title('Catenaria discreta')
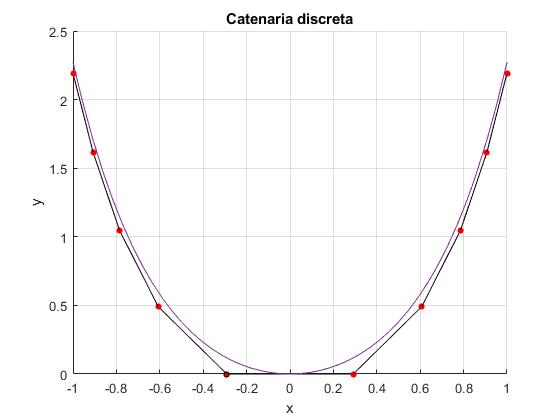
Con 21 eslabones, N=10, la cadena se hace casi indistinguible de la catenaria
Referencias
Beléndez, A., Beléndez, T. Neipp C. Estudio estático de un cable homogéneo bajo la acción de su propio peso: Catenaria. Revista Española de Física 15(4) 2001, págs. 38-42
C Y Wang. The optimum spanning catenary cable. Eur. J. Phys. 36(2015) 028001
Del apartado, 'La catenaria de longitud no especificada'
A Mareno, L Q English. The stability of the catenary shapes for a hanging cable of unspecified length. Eur. J. Phys.30 (2009) pp. 97–108
Del apartado, 'La catenaria discreta'
David Agmon, Hezi Yizhaq. A new solution of the discrete catenary problem. Eur. J. Phys. 41(2020) 025002

