Flexión de una viga en voladizo (I)

Una viga o una barra delgada son sólidos homogéneos e isótropos cuya longitud es grande comparada con las dimensiones de su sección trasversal.
Cuando una viga flexiona debido a las fuerzas exteriores que se aplican, existen algunas partes de la viga que se acortan y hay otras zonas que se alargan. Pero hay una línea, denominada neutra, que no se acorta ni se alarga. Esta línea se encuentra en el centro de gravedad de la sección trasversal y es la que representaremos en las simulaciones que vienen en esta página y en la siguiente.
Pequeñas flexiones
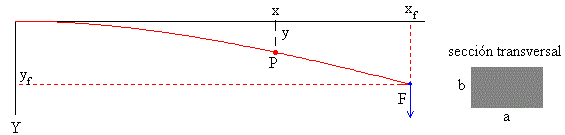
Consideremos una barra delgada de longitud L en posición horizontal, empotrada por un extremo y sometida a una fuera vertical F en el extremo libre. Determinaremos la forma de la barra y las coordenadas (xf, yf) del extremo libre para pequeñas flexiones de la barra.
Supondremos que
-
La barra tiene una longitud L mucho mayor que las dimensiones de su sección trasversal y que la deformación debida a su propio peso es despreciable.
-
Que la sección de la barra no cambia cuando se dobla. Cuando el espesor de la barra es pequeño comparado con el radio de curvatura, la sección trasversal cambia muy poco.
Que en estas condiciones es aplicable la ecuación de Euler-Bernoulli que relaciona el momento flector M de la fuerza aplicada y el radio de curvatura ρ de la barra deformada
El radio de curvatura de una función y(x) es
Para pequeñas pendientes (dy/dx)2≈0
Si despreciamos el peso de la propia barra, el momento de la fuerza F aplicada en el extremo libre, respecto del punto P (x, y) es M=F(xf-x)≈F(L-x)
Que integramos dos veces con las siguientes condiciones iniciales x=0, y=0, dy/dx=0.
El desplazamiento yf del extremo libre x=L es proporcional a la fuerza F aplicada
-
Y es el módulo de Young del material
-
I se denomina momento de inercia de la sección trasversal respecto de la fibra neutra
Se considera que la aproximación de pequeñas flexiones: el desplazamiento y del extremo libre de la barra, es proporcional a la fuerza F aplicada, produce resultados aceptables hasta un cierto valor del parámetro adimensional α<0.375, (véase al final del siguiente página) o bien, hasta un valor máximo de la fuerza aplicada Fm=2Y·I·α/L2
Actividades
Se introduce
- El material del que está hecho la barra, eligiéndolo en el control titulado Material
- La longitud de la barra L en cm, en el control titulado Longitud.
- El espesor b de la barra en mm, en el control titulado Espesor.
Se pulsa el botón titulado Nuevo.
- Se pulsa el botón izquierdo del ratón sobre una pesa
- de 10 g
- de 25 g
- de 50 g
- Cuando se deja de pulsar el botón izquierdo del ratón, se calcula y se representa la flexión de la barra. Se mide el desplazamiento del extremo libre.
- Se pulsa el botón izquierdo del ratón sobre otra pesa, se arrastra con el ratón y se cuelga del gancho inferior de la pesa precedente.
se arrastra con el ratón y se cuelga del extremo libre de la barra. El programa interactivo convierte el peso en g en fuerza en N, multiplicando por 10 y dividiendo por 1000. Por ejemplo, un peso de 100 g equivale a una fuerza de 1 N.
Cuando la fuerza F aplicada, es mayor que la fuerza máxima Fm=2Y·I·0.375/L2 el programa interactivo no permite colgar del extremo libre pesas adicionales, ya que se supone que la aproximación de pequeñas flexiones deja de ser aplicable.
Ejemplo:
- Sea L=50 cm=0.5 m, la longitud de la barra
- Sea b=0.78 mm=0.00078 m, el espesor de la barra
- La anchura a=0.03 m está fijada por el programa interactivo y no se puede cambiar
- Elegimos como material, el Acero
>> F=[10,20,30,40,50,60]*10/1000; %N, g=10 m/s^2
>> y_f=[1.70,3.41,5.11,6.82,8.52,10.23]/100; %m
>> plot(F,y_f,'ro','markersize',4,'markerfacecolor','r')
>> xlabel('F (N)')
>> ylabel('x_f (m)')
>> title('Módulo Y')
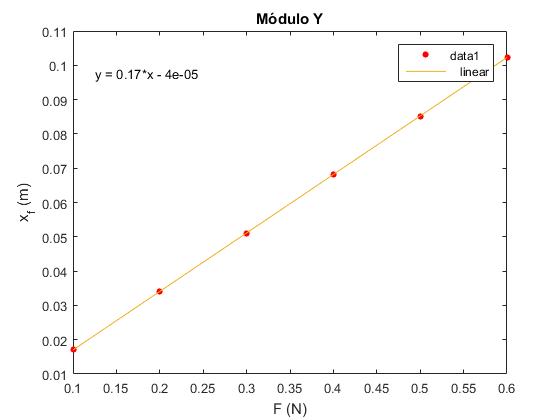
En el menú seleccionamos Tools/Basic Fitting, aparece un cuadro de diálogo donde marcamos la casilla linear en Plot fits. A continuación, pulsamos la flecha hacia la derecha --> para mostrar los coeficientes p1 y p2 del polinomio (recta) y=p1*x+p2 de ajuste.
Después de realizar la experiencia. La pendiente de la recta que relaciona la desviación del extremo libre y(L) con la fuerza aplicada F en dicho extremo es
m=0.17054 m/N
El momento de inercia I vale
Dada la pendiente (coeficiente de proporcionalidad de F) calculamos el módulo de Young Y

