Consideremos un cable flexible de longitud l, densidad λ por unidad de longitud, sujeto por ambos extremos a una barra rígida horizontal a una distancia x₀ del eje Y. Hemos demostrado que la forma que adopta el cable bajo la acción de su propio peso es una catenaria

En el punto más bajo de la catenaria, se engancha un peso mg, vamos a determinar la forma que adopta el cable

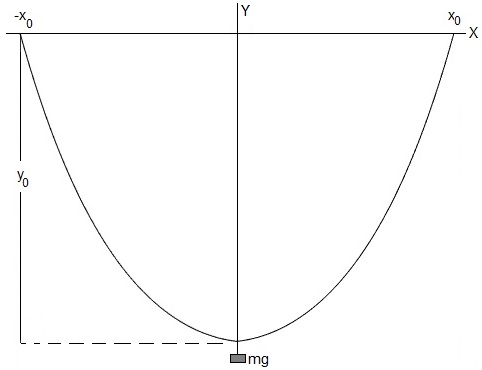
La forma que adopta el cable será la que haga mínima su energía potencial.

${\displaystyle y=-\frac{k}{\lambda g}+\frac{C_1}{\lambda g}\cosh \left(\frac{\lambda g}{C_1}x+C_2\right)}$

donde C₁, C₂ son constantes de integración a determinar, k es un parámetro a determinar

Utilizando la relación

${\displaystyle \begin{array}{l}\cosh (a+b)=\cosh (a)\cosh (b)+\sinh (a)\sinh (b)\\ =\left(\frac{e^a+e^{-a}}{2}\right)\left(\frac{e^b+e^{-b}}{2}\right)+\left(\frac{e^a-e^{-a}}{2}\right)\left(\frac{e^b-e^{-b}}{2}\right)=\frac{1}{2}{e}^a{e}^b+\frac{1}{2}{e}^{-a}{e}^{-b}\end{array}}$

Expresamos dicha ecuación de forma más conveniente

${\displaystyle y=-\frac{k}{\lambda g}+\frac{C_1}{2\lambda g}\left\{\exp \left(\frac{\lambda g}{C_1}x\right)\exp \left(C_2\right)+\exp \left(-\frac{\lambda g}{C_1}x\right)\exp \left(-C_2\right)\right\}}$

Llamando a=λg/C₁, b=exp(C₂), K=k/(λg), la ecuación se transforma en

${\displaystyle y=-K+\frac{1}{2a}\left(b{e}^{ax}+\frac{1}{b}{e}^{-ax}\right)}$

Ahora tenemos que determinar las constantes a, b y el parámetro K

Parámetro K

El parámetro K se determina sabiendo que y(x₀)=0. El cable está sujeto en este extremo.

${\displaystyle 0=-K+\frac{1}{2a}\left(b{e}^{a{x}_0}+\frac{1}{b}{e}^{-a{x}_0}\right)}$

La forma del cable está descrita por la ecuación

${\displaystyle y=\frac{1}{2a}\left\{b\left(e^{ax}-e^{a{x}_0}\right)+\frac{1}{b}\left(e^{-ax}-e^{-a{x}_0}\right)\right\},x>0}$

Esta ecuación describe la forma del cable para x>0. Dado que la forma del cable es simétrica, f(x)=f(-x). para x<0, hay que hacer los cambios

${\displaystyle \begin{array}{l}b\leftrightarrow \frac{1}{b},e^{a{x}_0}\leftrightarrow e^{-a{x}_0}\\ y=\frac{1}{2a}\left\{\frac{1}{b}\left(e^{ax}-e^{-a{x}_0}\right)+b\left(e^{-ax}-e^{a{x}_0}\right)\right\},x<0\end{array}}$

tal como se aprecia en el código MATLAB al final de esta página

La función que describe la forma del cable, es continua en x=0, pero su derivada (pendiente) no lo es

Constantes a y b

La longitud de la porción derecha x>0, del cable es

${\displaystyle \frac{l}{2}={\displaystyle \underset{0}{\overset{x_0}{\int }}\sqrt{1+{\left(\frac{dy}{dx}\right)}^2}dx}}$

Teniendo en cuenta que

${\displaystyle \begin{array}{l}\frac{dy}{dx}=\frac{1}{2}\left(b{e}^{ax}-\frac{1}{b}{e}^{-ax}\right)\\ \sqrt{1+{\left(\frac{dy}{dx}\right)}^2}=\frac{1}{2}\left(b{e}^{ax}+\frac{1}{b}{e}^{-ax}\right)\end{array}}$

El resultado es

${\displaystyle \begin{array}{l}\frac{l}{2}=\frac{1}{2}{\displaystyle \underset{0}{\overset{x_0}{\int }}\left(b{e}^{ax}+\frac{1}{b}{e}^{-ax}\right)dx}\\ \frac{l}{2}=\frac{1}{2a}\left\{b\left(e^{a{x}_0}-1\right)-\frac{1}{b}\left(e^{-a{x}_0}-1\right)\right\}\end{array}}$

La ordenada y₀ del punto medio x=0 es

${\displaystyle y_0=\frac{1}{2a}\left\{b\left(1-e^{a{x}_0}\right)+\frac{1}{b}\left(1-e^{-a{x}_0}\right)\right\}}$

Combinamos estas dos ecuaciones para obtener una ecuación trascendente cuya raíz es la constante a

${\displaystyle \begin{array}{l}\frac{l}{2}+y_0=\frac{1}{ab}\left(1-e^{-a{x}_0}\right)\\ \frac{l}{2}-y_0=\frac{b}{a}\left(e^{a{x}_0}-1\right)\\ \frac{l^2}{4}-y_0^2=\frac{2}{a^2}\left(\cosh \left(a{x}_0\right)-1\right)\end{array}}$

Conocido y₀, resolvemos esta ecuación trascendente para calcular la constante a, y luego, cualquiera de las dos ecuaciones para determinar la constante b

Centro de masa del cable homogéneo

Supondremos que la densidad λ del cable es constante

Como el cable es simétrico, el centro de masa se encuentra en el eje Y, x_cm=0, por lo que solamente es necesario calcular la ordenada y_cm

${\displaystyle y_{cm}=\frac{{\displaystyle \underset{-x_0}{\overset{x_0}{\int }}y·\lambda g·ds}}{{\displaystyle \underset{-x_0}{\overset{x_0}{\int }}\lambda g·ds}}=\frac{{\displaystyle \underset{-x_0}{\overset{x_0}{\int }}yds}}{l}=\frac{2{\displaystyle \underset{0}{\overset{x_0}{\int }}yds}}{l}}$

Es una integral que requiere de cierto trabajo para simplificar suficientemente el resultado

${\displaystyle \begin{array}{l}{y}_{cm}=\frac{2{\displaystyle \underset{0}{\overset{x_0}{\int }}\frac{1}{2a}\left\{\frac{1}{b}\left(e^{ax}-e^{-a{x}_0}\right)+b\left(e^{-ax}-e^{a{x}_0}\right)\right\}\sqrt{1+{\left(\frac{dy}{dx}\right)}^2}dx}}{l}=\\ \frac{2{\displaystyle \underset{0}{\overset{x_0}{\int }}\frac{1}{2a}\left\{\frac{1}{b}\left(e^{ax}-e^{-a{x}_0}\right)+b\left(e^{-ax}-e^{a{x}_0}\right)\right\}\left\{\frac{1}{2}\left(b{e}^{ax}+\frac{1}{b}{e}^{-ax}\right)\right\}dx}}{l}\\ =\frac{1}{2al}{\displaystyle \underset{0}{\overset{x_0}{\int }}\left\{b^2{e}^{2ax}+2-b^2{e}^{a{x}_0}{e}^{ax}-e^{a{x}_0}{e}^{-ax}+\frac{1}{b^2}{e}^{-2ax}-e^{-a{x}_0}{e}^{ax}-\frac{1}{b^2}{e}^{-a{x}_0}{e}^{-ax}\right\}dx}=\\ \frac{1}{2al}\left(-\frac{b^2}{2a}{e}^{2a{x}_0}+2x_0+\frac{1}{2b^{2}a}{e}^{-2a{x}_0}-\frac{b^2}{2a}+\frac{b^2}{a}{e}^{a{x}_0}-\frac{e^{a{x}_0}}{a}+\frac{e^{-a{x}_0}}{a}+\frac{1}{2b^{2}a}-\frac{e^{-a{x}_0}}{b^{2}a}\right)=\\ \frac{1}{4a^{2}l}\left\{-b^2\left(e^{2a{x}_0}-2e^{a{x}_0}+1\right)+\frac{1}{b^2}\left(e^{-2a{x}_0}-2e^{-a{x}_0}+1\right)+4x_{0}a-2e^{a{x}_0}+2e^{-a{x}_0}\right\}=\\ \frac{1}{4a^{2}l}\left\{-b^2{\left(1-e^{a{x}_0}\right)}^2+\frac{1}{b^2}{\left(1-e^{-a{x}_0}\right)}^2+4x_{0}a-4\sinh \left(a{x}_0\right)\right\}\end{array}}$

Comprobamos que los dos primeros sumandos son proporcionales al producto y₀l

${\displaystyle \begin{array}{l}{y}_{0}l=\frac{1}{2a}\left\{b\left(1-e^{a{x}_0}\right)+\frac{1}{b}\left(1-e^{-a{x}_0}\right)\right\}\frac{1}{a}\left\{b\left(e^{a{x}_0}-1\right)-\frac{1}{b}\left(e^{-a{x}_0}-1\right)\right\}=\\ \frac{1}{2a^2}\left\{-b^2{\left(1-e^{a{x}_0}\right)}^2+\frac{1}{b^2}{\left(1-e^{-a{x}_0}\right)}^2\right\}\end{array}}$

El resultado es

${\displaystyle y_{cm}=\frac{1}{4a^{2}l}\left(2a^2{y}_{0}l+4x_{0}a-4\sinh \left(a{x}_0\right)\right)=\frac{1}{2}{y}_0+\frac{1}{a^{2}l}\left(x_{0}a-\sinh \left(a{x}_0\right)\right)}$

Fuerza necesaria para deformar la catenaria

El cable sujeto por ambos extremos, adopta la forma de catenaria bajo la acción de su propio peso. Supongamos que ejercemos una fuerza F en la posición x=0, como consecuencia, dicha posición se desplaza a y₀

Cuando dicho punto se desplaza de y₀ a y₀+dy₀ bajo la acción de una fuerza F hacia abajo, se realiza un trabajo -F·dy₀, mientras que la energía potencial cambia en Mg·dy_cm, siendo M la masa del cable.

${\displaystyle F=-Mg\frac{d{y}_{cm}}{d{y}_0}}$

Dada la energía potencial, E_p(x), la fuerza se obtiene derivando con respecto a x y cambiando de signo, F=-dE_p(x)/dx

Ahora bien, y_cm depende de dos variables y₀ y a

${\displaystyle \frac{d{y}_{cm}}{d{y}_0}=\frac{\partial y_{cm}}{\partial y_0}+\frac{\partial y_{cm}}{\partial a}\frac{da}{d{y}_0}}$

Obtenemos las expresiones de las derivadas y de las derivadas parciales

${\displaystyle \begin{array}{l}\frac{l^2}{4}-y_0^2=2\frac{\cosh \left(a{x}_0\right)-1}{a^2}\\ -2y_0\frac{d{y}_0}{da}=2\frac{x_0\sinh \left(a{x}_0\right)·a^2-2a\left(\cosh \left(a{x}_0\right)-1\right)}{a^4}\\ \frac{da}{d{y}_0}=\frac{a^3{y}_0}{2\cosh \left(a{x}_0\right)-a{x}_0\sinh \left(a{x}_0\right)-2}\\ \frac{\partial y_{cm}}{\partial y_0}=\frac{1}{2}\\ \frac{\partial y_{cm}}{\partial a}=\frac{1}{l}\frac{\left(x_0-x_0\cosh \left(a{x}_0\right)\right)a^2-2a\left(x_{0}a-\sinh \left(a{x}_0\right)\right)}{a^4}\end{array}}$

El resultado es

${\displaystyle \begin{array}{l}\frac{d{y}_{cm}}{d{y}_0}=\frac{1}{2}+\frac{1}{l}\frac{\left(x_0-x_0\cosh \left(a{x}_0\right)\right)a^2-2a\left(x_{0}a-\sinh \left(a{x}_0\right)\right)}{a^4}\frac{a^3{y}_0}{2\cosh \left(a{x}_0\right)-a{x}_0\sinh \left(a{x}_0\right)-2}=\\ \frac{1}{2}+\frac{y_0}{l}\frac{2\sinh \left(a{x}_0\right)-a{x}_0-a{x}_0\cosh \left(a{x}_0\right)}{2\cosh \left(a{x}_0\right)-2-a{x}_0\sinh \left(a{x}_0\right)}\end{array}}$

Teniendo en cuenta las relaciones

${\displaystyle \begin{array}{l}\cosh \alpha -1=2{\sinh }^2\left(\frac{\alpha }{2}\right)\\ \cosh \alpha +1=2{\cosh }^2\left(\frac{\alpha }{2}\right)\\ \sinh \alpha =2\cosh \left(\frac{\alpha }{2}\right)\sinh \left(\frac{\alpha }{2}\right)\end{array}}$

La fracción se simplifica notablemente

${\displaystyle \begin{array}{l}\frac{d{y}_{cm}}{d{y}_0}=\frac{1}{2}+\frac{y_0}{l}\frac{4\sinh \left(\frac{a{x}_0}{2}\right)\cosh \left(\frac{a{x}_0}{2}\right)-2a{x}_0{\cosh }^2\left(\frac{a{x}_0}{2}\right)}{4{\sinh }^2\left(\frac{a{x}_0}{2}\right)-2a{x}_0\sinh \left(\frac{a{x}_0}{2}\right)\cosh \left(\frac{a{x}_0}{2}\right)}=\\ \frac{d{y}_{cm}}{d{y}_0}=\frac{1}{2}+\frac{y_0}{l}\frac{\cosh \left(\frac{a{x}_0}{2}\right)}{\sinh \left(\frac{a{x}_0}{2}\right)}\end{array}}$

La fuerza F vale

${\displaystyle F=-Mg\left(\frac{1}{2}+\frac{y_0}{l}\frac{\cosh \left(\frac{a{x}_0}{2}\right)}{\sinh \left(\frac{a{x}_0}{2}\right)}\right)}$

Caso particular: la catenaria

Partimos de la ecuación que describe la forma del cable para x>0

${\displaystyle y=\frac{1}{2a}\left\{b\left(e^{ax}-e^{a{x}_0}\right)+\frac{1}{b}\left(e^{-ax}-e^{-a{x}_0}\right)\right\},x>0}$

Si ahora hacemos que y(-x₀)=0

${\displaystyle \begin{array}{l}0=\frac{1}{2a}\left\{b\left(e^{-a{x}_0}-e^{a{x}_0}\right)+\frac{1}{b}\left(e^{a{x}_0}-e^{-a{x}_0}\right)\right\}\\ b^2=1\end{array}}$

La ecuación que obtenemos es

${\displaystyle y=\frac{1}{2a}\left\{\left(e^{ax}-e^{a{x}_0}\right)+\left(e^{-ax}-e^{-a{x}_0}\right)\right\}=\frac{1}{a}\left\{\cosh \left(ax\right)-\cosh \left(a{x}_0\right)\right\}}$

que es la ecuación de la catenaria

La ordenada y₀ del punto medio x=0 es

${\displaystyle y_0=\frac{1}{2a}\left\{\left(1-e^{a{x}_0}\right)+\left(1-e^{-a{x}_0}\right)\right\}=\frac{1}{a}\left(1-\cosh \left(a{x}_0\right)\right)}$

La constante a se calcula a partir de la longitud del cable con b=1

${\displaystyle \frac{l}{2}=\frac{\sinh \left(a{x}_0\right)}{a}}$

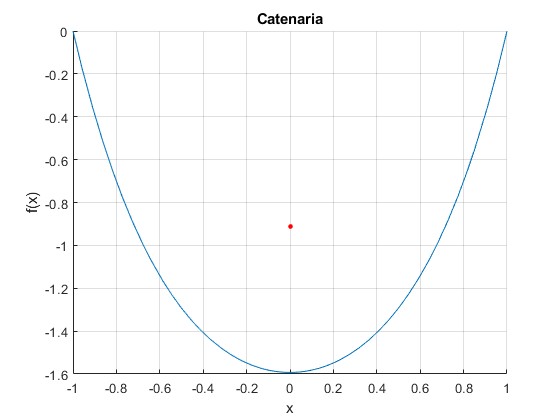
Sea un cable de longitud l=4, se cuelga de una barra rígida horizontal, estando los extremos separados 2x₀=2. Calculamos la constante a=2.1773, resolviendo la ecuación trascendente, y la flecha y₀=-1.5928. Representamos la catenaria y la posición de su centro de masas mediante un punto de color rojo

x0=1; %extremo derecho
l=4; %longitud
f=@(a) sinh(a*x0)/a-l/2;
a=fzero(f,[0.01,5]);
y0=(1-cosh(a*x0))/a; %flecha
y_cm=y0/2+(x0*a-sinh(x0*a))/(a^2*l); %centro de masas
hold on
f=@(x) (cosh(a*x)-cosh(a*x0))/a;
fplot(f,[-x0,x0])
plot(0,y_cm,'ro','markersize',3,'markerfacecolor','r')
hold off
grid on
xlabel('x')
ylabel('f(x)')
title('Catenaria')

a =    2.1773
y0 =   -1.5928

Caso general

Las ecuaciones que describen la foma del cable son

${\displaystyle \begin{array}{l}y=\frac{1}{2a}\left\{b\left(e^{ax}-e^{a{x}_0}\right)+\frac{1}{b}\left(e^{-ax}-e^{-a{x}_0}\right)\right\},x>0\\ y=\frac{1}{2a}\left\{\frac{1}{b}\left(e^{ax}-e^{-a{x}_0}\right)+b\left(e^{-ax}-e^{a{x}_0}\right)\right\},x<0\end{array}}$

Dada la flecha y₀ se calcula la constante a resolviendo la ecuación trascendente

${\displaystyle \frac{l^2}{4}-y_0^2=\frac{2}{a^2}\left(\cosh \left(a{x}_0\right)-1\right)}$

Con cualquiera de las otras dos ecuaciones calculamos la constante b

${\displaystyle y_0=\frac{1}{2a}\left\{b\left(1-e^{a{x}_0}\right)+\frac{1}{b}\left(1-e^{-a{x}_0}\right)\right\}}$

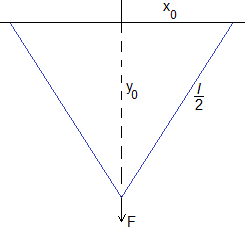
Cuando aplicamos una fuerza infinita, la cuerda adopta la forma de un triángulo isósceles.

El máximo valor de y₀ es

${\displaystyle y_0=\sqrt{\frac{l^2}{4}-x_0^2}}$

Con los datos l=4 y x₀=1, obtenemos $y_0=-\sqrt{3}\approx -\text{1}\text{.7321}$. Recordamos que para la catenaria y₀=-1.5928.

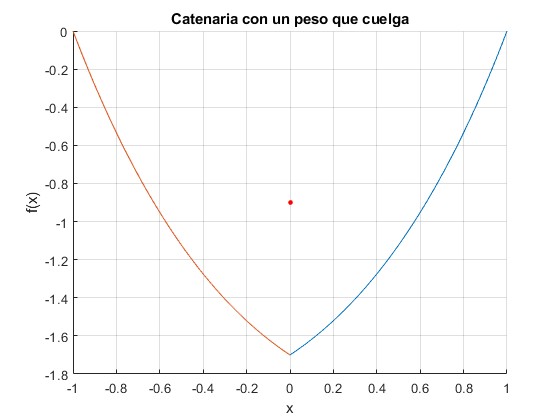
Vamos a representar la forma del cable para y₀=-1.7. La fuerza que se aplica es F=0.3337Mg. Como vemos el cable adopta una forma casi triangular. El punto de color rojo marca la posición del centro de masas

x0=1;
l=4;
y0=-1.7;
f=@(a) (cosh(a*x0)-1)*2/a^2+y0^2-l^2/4;
a=fzero(f,[0.01,5]);
b=(a*l+sqrt(a^2*l^2+4*(exp(a*x0)-1)*(exp(-a*x0)-1)))/(2*(exp(a*x0)-1));
% y_0=(b*(1-exp(a*x0))+(1-exp(-a*x0))/b)/(2*a);

y_cm=y0/2+(x0*a-sinh(x0*a))/(a^2*l); %centro de masas
F=1/2+y0*cosh(a*x0/2)/(l*sinh(a*x0/2)); %fuerza
disp(-F)
f=@(x) (b*(exp(a*x)-exp(a*x0))+(exp(-a*x)-exp(-a*x0))/b)/(2*a);
hold on
fplot(f,[0,x0])
f=@(x) ((exp(a*x)-exp(-a*x0))/b+b*(exp(-a*x)-exp(a*x0)))/(2*a);
fplot(f,[-x0,0])
plot(0,y_cm,'ro','markersize',3,'markerfacecolor','r')
hold off
grid on
xlabel('x')
ylabel('f(x)')
title('Catenaria con un peso que cuelga')

    0.3337
>> a,b
a =    1.1249
b =    2.0011

Cambiamos y₀=-1.0. La fuerza que se aplica es hacia arriba F=-0.2389Mg

 -0.2389
>> a,b
a =    3.8266
b =    0.2556

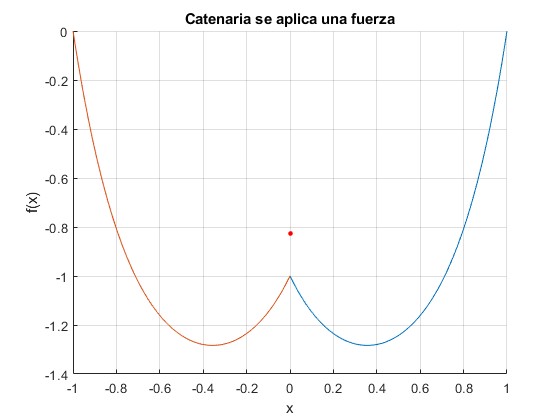
Cuando y₀=0. La fuerza que se aplica es hacia arriba F=-0.5Mg

 -0.5000
>> >> a,b
a =    4.3546
b =    0.1133

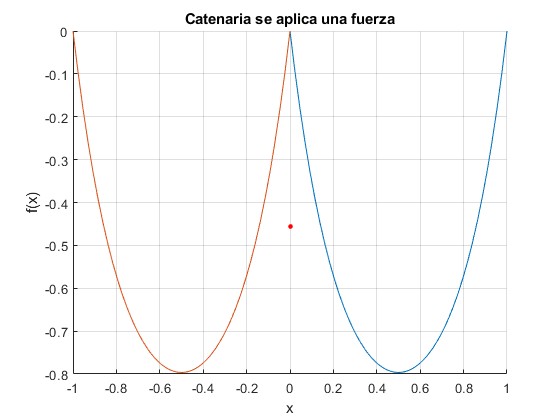
Referencias

Harold S. Zapolsky. A simple solution of the center loaded catenary. Am. J. Phys. 58 (11) November 1990. pp. 1110-1112