La cuerda tiene la misma forma cualquiera que sea el ángulo de rotación. En cambio, si consideramos el peso, la cuerda ya no tiene la misma forma cuando se encuentra arriba que abajo o a cualquier otro ángulo intermedio, el problema se vuelve muy complejo

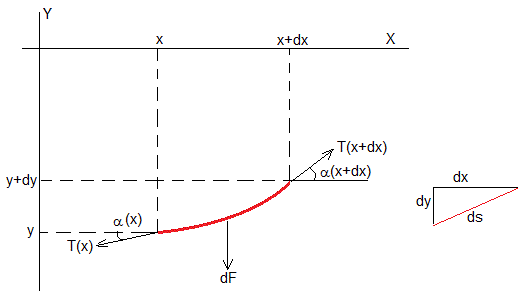
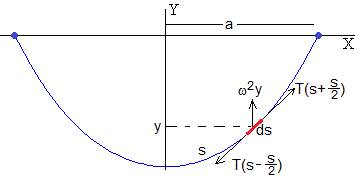
Consideremos un elemento diferencial ds de cuerda. Dibujamos las fuerzas sobre dicho elemento.

• La fuerza aplicada dF(x)
• La tensión T(x), que ejerce la parte izquierda de la cuerda sobre dicho elemento
• La tensión T(x+dx), que ejerce la parte derecha de la cuerda sobre dicho elemento

Ecuaciones de equilibrio

• Equilibrio a lo largo del eje X

T(x+dx)·cosα(x+dx)-T(x)·cosα(x)=0

• Equlibrio a lo largo del eje Y

T(x+dx)·sinα(x+dx)-T(x)·cosα(x)-dF(x)=0

La primera ecuación es equivalente a d(T(x)·cosα(x))=0, o bien,

${\displaystyle T(x)\cos \left(\alpha (x)\right)=T_0}$

siendo T₀ es la tensión de la cuerda para α=0

Dividiendo la segunda entre la primera

${\displaystyle \begin{array}{l}\frac{T(x+dx)·\sin \left(\alpha (x+dx)\right)}{T(x+dx)·\cos \left(\alpha (x+dx)\right)}-\frac{T(x)·\sin \left(\alpha (x)\right)}{T(x)·\cos \left(\alpha (x)\right)}=\frac{dF(x)}{T_0}\\ T_0\left(\tan \left(\alpha (x+dx)\right)-\tan \left(\alpha (x)\right)\right)=dF(x)\end{array}}$

La pendiente de la recta tangente a la curva y=y(x) en x es

${\displaystyle \tan \alpha (x)={\left(\frac{dy}{dx}\right)}_x}$

La ecuaciones de equilibrio se escriben

${\displaystyle \begin{array}{l}{\left(\frac{dy}{dx}\right)}_{x+dx}-{\left(\frac{dy}{dx}\right)}_x=\frac{1}{T_0}dF\\ \frac{d}{dx}\left\{{\left(\frac{dy}{dx}\right)}_{x+dx}-{\left(\frac{dy}{dx}\right)}_x\right\}=\frac{1}{T_0}\frac{dF}{dx}\\ \frac{d^{2}y}{d{x}^2}=\frac{1}{T_0}\frac{dF}{dx}\end{array}}$

Dependiendo de la expresión de la fuerza externa dF/dx, obtenemos distintas ecuaciones diferenciales y así distintas soluciones para la forma de la curva

La catenaria

El peso de un elemento ds de cuerda es dF=λg·ds, siendo λ la densidad lineal y $ds=\sqrt{d{x}^2+d{y}^2}$, la longitud del elemento diferencial de cuerda

${\displaystyle \frac{dF}{dx}=\frac{dF}{ds}\frac{ds}{dx}=\lambda g\sqrt{1+{\left(\frac{dy}{dx}\right)}^2}}$

La ecuación diferencial de la catenaria que se ha estudiado en la página titulada La catenaria es

${\displaystyle \frac{d^{2}y}{d{x}^2}=\frac{\lambda g}{T_0}\sqrt{1+{\left(\frac{dy}{dx}\right)}^2}}$

Forma de la cuerda que gira

Supongamos que los extremos de la cuerda están atados a un eje (el X) que gira con velocidad angular constante ω. En el sistema de referencia en rotación los elementos de la cuerda experimentan una fuerza centrífuga proporcional al radio -y (en la figura y es negativo) de la circunferencia que describen. La fuerza centrífuga es similar al peso, es proporcional a la masa. La aceleración de dicho elemento es -ω²y. En la ecuación diferencial de la catenaria reemplazamos g por -ω²y

${\displaystyle \frac{d^{2}y}{d{x}^2}=-\frac{\lambda {\omega }^2}{T_0}y\sqrt{1+{\left(\frac{dy}{dx}\right)}^2}}$

Llamamos 1/L² a la constante de proporcionalidad, que tiene dimensión de longitud.

Resolvemos la ecuación diferencial con las condiciones en los extremos y(0)=0 e y(a)=0.

Solución aproximada

Si la deformación de la cuerda no es muy grande, se cumple que la pendiente dy/dx en todos los puntos de la cuerda es pequeña

${\displaystyle {\left(\frac{dy}{dx}\right)}^2<<1}$

Por lo que la solución de la ecuación diferencial es sencilla, recuerda a la de un Movimiento Armónico Simple

${\displaystyle \begin{array}{l}\frac{d^{2}y}{d{x}^2}=-\frac{1}{L^2}y\\ y(x)=y_m\sin \left(\frac{x}{L}+\phi \right)\end{array}}$

y_m es la amplitud que tiene que ser pequeña, la frecuencia angular es 1/L y φ la fase inicial. La distancia entre los extremos de la cuerda sujetos al eje es medio periodo, Δx=π/(1/L)=πL, tal como se ve en la figura

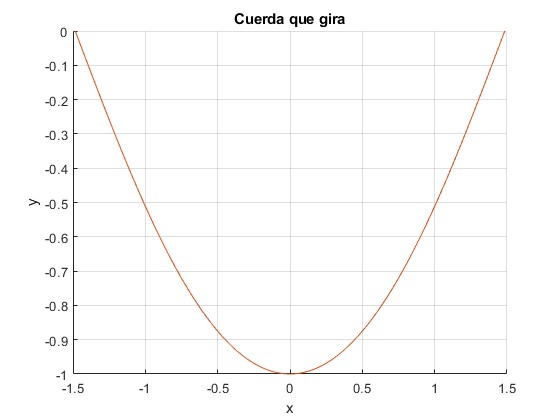
L=1/pi;
g=@(x) sin(x/L-pi/2);
fplot(g,[-0.5,0.5])
grid on
xlabel('x')
ylabel('y')
title('Cuerda que gira')

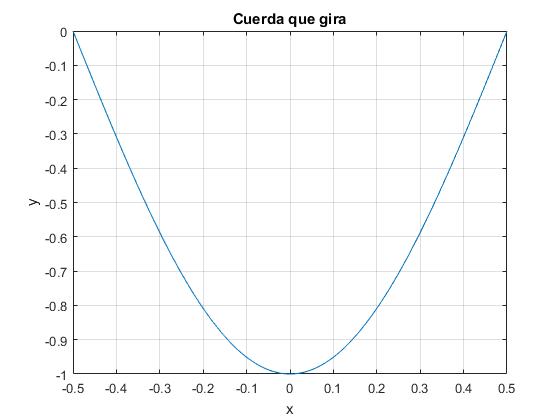
Como vemos la cuerda está sujeta en los puntos x=-0.5 y x=0.5. Falta multiplicar la función seno por una amplitud y_m pequeña, para simular la deformación de la cuerda que gira con velocidad angular ω pequeña.

Solución analítica

${\displaystyle \begin{array}{l}\frac{d}{dx}\sqrt{1+{\left(\frac{dy}{dx}\right)}^2}=\frac{\frac{dy}{dx}\frac{d^{2}y}{d{x}^2}}{\sqrt{1+{\left(\frac{dy}{dx}\right)}^2}}\\ \frac{d}{dx}\sqrt{1+{\left(\frac{dy}{dx}\right)}^2}=-\frac{y}{L^2}\frac{dy}{dx}\\ \sqrt{1+{\left(\frac{dy}{dx}\right)}^2}=-\frac{1}{2L^2}{y}^2+C\end{array}}$

Escribimos esta ecuación de la forma equivalente

${\displaystyle \sqrt{1+{\left(\frac{dy}{dx}\right)}^2}=1+\frac{1}{2L^2}\left(y_m^2-y^2\right)}$

donde y_m es una constante a determinar. Elevamos al cuadrado y ordenamos los términos para que nos salga una ecuación diferencial del tipo

${\displaystyle {\left(\frac{dz}{du}\right)}^2=\left(1-z^2\right)\left(1-p^2{z}^2\right)}$

cuya solución es z=sn(u,p), véase Wikipedia, Jacobi elliptic functions o Integrales elípticas

${\displaystyle \begin{array}{l}u\left(z,p^2\right)={\displaystyle \underset{0}{\overset{z}{\int }}\frac{dz}{\sqrt{\left(1-p^2{z}^2\right)\left(z^2-1\right)}}}\\ z=\text{sn}\left(u,p\right)\end{array}}$

En este problema

${\displaystyle \begin{array}{l}{\left(\frac{dy}{dx}\right)}^2=\frac{1}{2L^2}\left(y_m^2-y^2\right)\left\{\left(1+\frac{y_m^2}{4L^2}\right)-\frac{y^2}{4L^2}\right\}\\ y_m^2{\left(\frac{d\left(y/y_m\right)}{dx}\right)}^2=\frac{y_m^2}{L^2}\left(1+\frac{y_m^2}{4L^2}\right)\left(1-{\left(\frac{y}{y_m}\right)}^2\right)\left\{1-\left(\frac{y_m^2}{4L^2+y_m^2}\right){\left(\frac{y}{y_m}\right)}^2\right\}\end{array}}$

con

${\displaystyle z=\frac{y}{y_m},u=\frac{x}{L}\sqrt{1+\frac{y_m^2}{4L^2}},p^2=\frac{y_m^2}{4L^2+y_m^2}}$

La solución z=sn(u, p) se transforma en

${\displaystyle y(x)=y_m\text{sn}\left(\frac{x}{L}\sqrt{1+\frac{y_m^2}{4L^2}}+\phi ,p\right)}$

Como se ha comprobado en la página titulada Integrales elípticas, medio periodo de la función sn(u,p) es Δu=2K(p) lo que corresponde a

${\displaystyle \begin{array}{l}\Delta u=\frac{\Delta x}{L}\sqrt{1+\frac{y_m^2}{4L^2}}\\ \Delta x=\Delta u\frac{L}{\sqrt{1+\frac{y_m^2}{4L^2}}}=2K(p)\frac{L}{\sqrt{1+\frac{y_m^2}{4L^2}}}\end{array}}$

Siendo K(p) la integral elíptica completa de primera especie. Δx es la distancia entre los extremos de la cuerda e y_m es la amplitud

Sea

L=1/pi;
ym=1;
p=sqrt(ym^2/(4*L^2+ym^2));
K=ellipke(p^2); 
Dx=2*K*L/(sqrt(1+ym^2/(4*L^2))); %distancia entre los extremos
alfa=sqrt(1+ym^2/(4*L^2))/L;
f=@(x) -ellipj(alfa*x+K,p^2);
hold on
fplot(f,[-Dx/2,Dx/2])
g=@(x) ym*sin(x/L-pi/2);
fplot(g,[-pi*L/2,pi*L])
hold off
ylim([-1,0])
legend('exacta','aproximada', 'location','best')
grid on
xlabel('x')
ylabel('y')
title('Cuerda que gira')

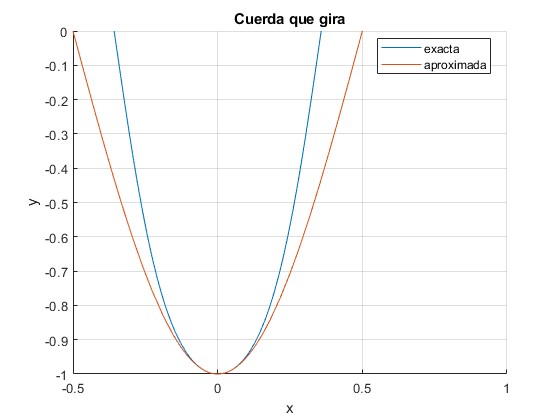
La solución exacta y aproximada difieren

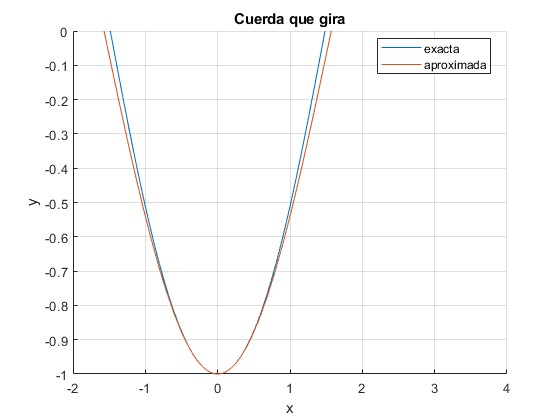
Cuando L=1, la solución exacta y aproximada casi coinciden

Procedimiento numérico

Este problema nos da la oportunidad de resolver una ecuación diferencial con condiciones en los extremos y comparar la solución numérica aplicando el procedimiento bvp4c de MATLAB y la solución analítica

${\displaystyle \begin{array}{l}\frac{d^{2}y}{d{x}^2}=-\frac{y}{L^2}\sqrt{1+{\left(\frac{dy}{dx}\right)}^2}\hfill \\ y(x)=y_m\text{sn}\left(\frac{x}{L}\sqrt{1+\frac{y_m^2}{4L^2}}+K(p),p\right)\hfill \end{array}}$

Los pasos para aplicar el procedimiento bvp4c son

• Una funcion que define la ecuación diferencial, lo mismo que en el procedimiento ode45

f=@(~,x) [x(2), -x(1)*sqrt(1+x(2)^2)/L^2];

• Una función que especifica las condiciones en los extremos

Para -Δx/2, y=0 (extremo izquierdo de la cuerda), para Δx/2, y=0 (extremo derecho de la cuerda)

g=@(xa,xb) [xa(1), xb(1)];

• La aproximación inicial, que va a consistir en la función ym*sin(x/L-pi/2) y su derivada la función coseno

xIni=linspace(-Dx/2, Dx/2,100);
aprox=@(x) [ym*sin(x/L-pi/2), ym*cos(x/L-pi/2)/L];
solinit = bvpinit(xIni, aprox); %primera aproximación

Representamos la función exacta y la función calculada mediante el procedimiento bvp4c de MATLAB. No hay diferencias apreciables entre ambas

L=1/pi;
ym=1;
p=sqrt(ym^2/(4*L^2+ym^2));
K=ellipke(p^2); 
Dx=2*K*L/(sqrt(1+ym^2/(4*L^2))); %distancia entre los extremos
alfa=sqrt(1+ym^2/(4*L^2))/L;
fe=@(x) -ellipj(alfa*x+K,p^2); %exacta
%aproximada
f=@(~,x) [x(2), -x(1)*sqrt(1+x(2)^2)/L^2];
g=@(xa,xb) [xa(1), xb(1)];
xIni=linspace(-Dx/2, Dx/2,100);
aprox=@(x) [ym*sin(x/L-pi/2), ym*cos(x/L-pi/2)/L];
solinit = bvpinit(xIni, aprox); %primera aproximación
sol1 = bvp4c(f, g, solinit); 
y = deval(sol1,xIni);
hold on
fplot(fe,[-Dx/2, Dx/2])
plot(xIni,y(1,:));
hold off
grid on
xlabel('x')
ylabel('y')
title('Cuerda que gira'

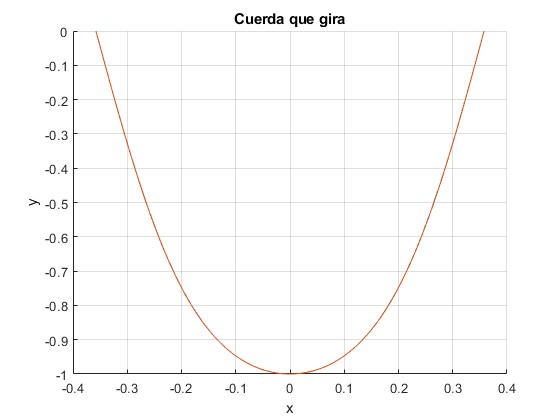
Cambiamos el parámetro L=1

Deducción alternativa

En este apartado volvemos a deducir la ecución diferencial de la forma de la cuerda en movimiento de rotación con velocidad angular ω

Consideramos un elemento infinitesimal de la cuerda de longitud ds y masa dm=λds. Hay aceleración centrípetra en la dirección vertical Y. El elemento ds describe una circunferencia de radio y con velocidad angular constante ω. No hay aceleración en la dirección horizontal X.

${\displaystyle \{\begin{array}{l}{T}_x\left(s+\frac{ds}{2}\right)-T_x\left(s-\frac{ds}{2}\right)=0\\ T_y\left(s+\frac{ds}{2}\right)-T_y\left(s-\frac{ds}{2}\right)={\omega }^2(-y)dm\end{array}}$

o bien,

${\displaystyle \{\begin{array}{l}\frac{d{T}_x}{ds}=0\\ \frac{d{T}_y}{ds}=-\lambda {\omega }^{2}y\end{array}}$

donde λ es la densidad lineal de la cuerda.

Integrando la primera, tenemos T_x=T₀. La componente horizontal de la tensión de la cuerda es constante en todos los puntos y es igual a la tensión de la cuerda en su punto más bajo.

Como la tensión T es tangente a la cuerda, se cumple

${\displaystyle \frac{dy}{dx}=\frac{T_y}{T_x}=\frac{T_y}{T_0}}$

Por otra parte, la longitud ds del elemento infinitesimal de la cuerda es

${\displaystyle ds=\sqrt{d{x}^2+d{y}^2}=\sqrt{1+{\left(\frac{dy}{dx}\right)}^2}dx}$

La ecuación diferencial de la forma de la cuerda es

${\displaystyle \begin{array}{l}\frac{d{T}_y}{ds}=-\lambda {\omega }^{2}y\\ \frac{d\left(T_0\frac{dy}{dx}\right)}{\sqrt{1+{\left(\frac{dy}{dx}\right)}^2}dx}=-\lambda {\omega }^{2}y\\ \frac{\frac{d^{2}y}{d{x}^2}}{\sqrt{1+{\left(\frac{dy}{dx}\right)}^2}}=-\frac{\lambda {\omega }^2}{T_0}y\end{array}}$

Integrando

${\displaystyle \sqrt{1+{\left(\frac{dy}{dx}\right)}^2}=-\frac{1}{2}\frac{\lambda {\omega }^2}{T_0}{y}^2+C}$

Energía mínima

La energía cinética de la mitad de la cuerda es

${\displaystyle E={\displaystyle \underset{0}{\overset{l}{\int }}\frac{1}{2}dm{\left(\omega y\right)}^2}=\frac{1}{2}{\omega }^2{\displaystyle \underset{0}{\overset{l}{\int }}{y}^2\left(\lambda ds\right)}=\frac{1}{2}\lambda {\omega }^2{\displaystyle \underset{0}{\overset{a}{\int }}{y}^2\sqrt{1+{\left(\frac{dy}{dx}\right)}^2}dx}}$

ωy es la velocidad tangencial del elemento diferencial ds de la cuerda

La energía deberá ser mínima con la restricción de que la longitud de la cuerda 2l es constante

${\displaystyle l={\displaystyle \underset{0}{\overset{a}{\int }}\sqrt{1+{\left(\frac{dy}{dx}\right)}^2}dx}}$

Un problema similar al estudiado en la catenaria. Formamos la función F dependiente de un parámetro k

${\displaystyle F(x,y,\dot{y})=\frac{1}{2}\lambda {\omega }^2{y}^2\sqrt{1+{\dot{y}}^2}+k\sqrt{1+{\dot{y}}^2}}$

Aplicando la ecuación de Euler-Lagrange a la función F que no depende de x

${\displaystyle \begin{array}{l}\dot{y}\frac{\partial F}{\partial \dot{y}}-F=C\hfill \\ \dot{y}\left(\lambda {\omega }^2{y}^2\frac{\dot{y}}{2\sqrt{1+{\dot{y}}^2}}+k\frac{\dot{y}}{\sqrt{1+{\dot{y}}^2}}\right)-\frac{1}{2}\lambda {\omega }^2{y}^2\sqrt{1+{\dot{y}}^2}-k\sqrt{1+{\dot{y}}^2}\hfill \\ \begin{array}{l}\lambda {\omega }^2{y}^2{\dot{y}}^2+k{\dot{y}}^2-\lambda {\omega }^2{y}^2\left(1+{\dot{y}}^2\right)-k\left(1+{\dot{y}}^2\right)=2C\sqrt{1+{\dot{y}}^2}\\ -\lambda {\omega }^2{y}^2-k=2C\sqrt{1+{\dot{y}}^2}\\ \sqrt{1+{\left(\frac{dy}{dx}\right)}^2}=-\frac{\lambda {\omega }^2}{2C}{y}^2-\frac{k}{2C}\end{array}\hfill \end{array}=C}$

Obtenemos una ecuación similar

Referencias

Arne Nordmark, Hanno Essén. The skipping rope curve. Eur. J. Phys. 28 (2007) 241-247

Pirooz Mohazzabi, Jeffrey R. Schmidt. Profile of a rotating string. Can. J. Phys. 77: 505–513 (1999)