Malguki bertikal batek plataforma bat du gainean,

eta goitik bloke bat erortzen zaio

Dinamika

Talkak

Tanke higikor batek
tiro egiten du

Erorketa askea eta
ondorengo erreboteak

Pendulu biren
arteko talkak

Aurrez-aurreko talkak
(dimentsio bakarrean)

Aurrez-aurreko
talka elastiko bi

Etengabeko talka
elastikoak
karril batean

Aurrez-aurreko
talka bertikalak

Iraupen luzeko
talka inelastikoa

Pendulu balistikoa

Momentu lineala
kontserbatzen ez den
pendulu balistikoa

Talka inelastikoa
malguki baten gainean

Bala baten
abiadura neurtzea

Bi dimentsiotako
talkak

Penduluen segida

Higidura-ekuazioa

Energiaren balantzea

Higiduraren ekuazio-diferentziala

Saiakuntza

Malguki bertikal batek plataforma bat du gainean, eta bere gainetik, h altueratik, bloke bat erortzen zaio. Malgukiaren konstantea k da, plataformaren masa M eta blokearena m. Blokearen eta plataformaren arteko talka inelastikoa da eta itsatsita geratzen dira. Kalkula bedi talkaren ondoren nola mugituko diren malgukia, plataforma eta blokea.

Higiduraren ekuazioa

Malgukiaren oreka-posizioa, M masadun plataforma gainean duela.

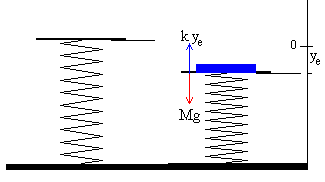Malgukia eta plataforma orekan daudenean, plataformaren pisua eta malgukiak egiten dion indarra berdinak dira. Dei diezaiogun posizio horri, y_e :

k·y_e =Mg

Plataformaren gainetik, h+y_e altueran, blokea erortzen da pausagunetik abiatuta, eta plataformarekin talka egiten du.

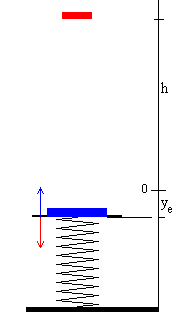Blokearen abiadura, justu plataformarekin talka egin baino lehen:

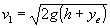
Momentu linealaren kontserbazioa:

Talkaren iraupena nulutzat hartuko dugu, eta horrela bikotea isolatua da, beraz momentu linealaren kontserbazioa aplika daiteke:

mv₁=(m+M)v₀.

Malgukiaren oreka-posizioa, M masadun plataforma eta m masadun blokea gainean dituela.

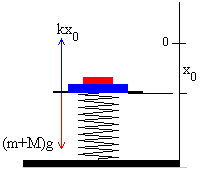Malgukiak, plataforma eta blokea eusten dituenean, orekan, plataformaren eta blokearen pisuak berdintzen ditu. Dei diezaiogun posizio horri, y₀ :

k·x₀=(M+m)g

Gero multzoak oszilatu egiten du:

Alegia, Higidura Harmoniko Sinpleaz mugituko da, eta periodoa:

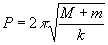
Maiztasun angeluarra: w =2p /P

Hona hemen, higidura harmoniko sinplearen ekuazioa:

x= -x₀+A·sin(w t+j )

Eta adierazpen hori denborarekiko deribatuz, multzoaren abiadura lortzen da:

v=Aw ·cos(w t+j )

A anplitudea eta hasierako fasea, j , hasierako baldintzetatik kalkulatzen dira:

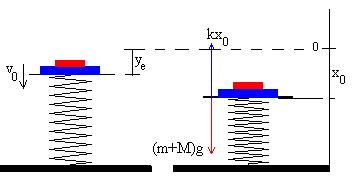
Irudiak erakusten duenez, hasieran (t=0) multzoaren posizioa -y_e da eta hasierako abiadura v₀ , hain zuzen, multzoak justu talkaren ondoren duena.

Eta horrela ekuazio bi ditugu eta ezezagun bi:

-y_e = -x₀+A·sinj
-v₀=Aw ·cosj

Ekuazio horien emaitzak dira A eta j .

Adibidea

Esate baterako:

Blokearen masa, m=10 kg
Plataformaren masa, M=20 kg
Malgukiaren konstantea, k=2000 N/m

Altueraren jatorria hartzen da, malgukiaren oreka posizioan, deformaziorik gabe dagoenean. Blokea posizio horrekiko 1m-ko altueratik erortzen uzten da.

Malgukiaren oreka-posizioa, gainean plataforma bakarrik duenean.

20·9.8=2000·y_e eta hortik y_e=9.8 cm

Blokearen abiadura talka baino lehen:

Blokea erortzen uzten denean, bere altuera 1.098 m da, eta abiadura:

v₁=4.64 m/s

Blokeak plataformaren kontra talka egiten du:

10·4.64=(10+20)·v₀ eta hortik v₀=1.546 m/s edo 154.6 cm/s

Malgukiaren oreka-posizioa, gainean plataforma eta blokea dituenean.

(20+10)·9.8=2000·x₀, eta hortik x₀=14.7 cm

Higidura Harmoniko Sinplea

Oszilazioen periodoa

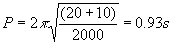
maiztasun angeluarra w =8.16 rad/s

Higidura Harmoniko Sinplearen ekuazioa:

x= -14.7+A·sin(w t+j ) cm
v= Aw ·cos(w t+j ) cm/s

Hasierako baldintzak, t=0, x₀= -14.7 cm, y_e= -9.8 cm eta v₀=154.6 cm/s.

-9.8= -14.7+A·sinj
-154.6=Aw · cosj

j =165.5º=2.89 rad
A=19.56 cm

Higidura Harmoniko Sinplearen ekuazioa:

x= -14.7+19.56·sin(8.16t+2.89) cm

Multzoak posiziorik baxuena atzematen du, ekuazioan honako baldintza betetzen denean: sin(w t+j )=-1, beraz, 8.16t+2.89=3π/2, eta hortik aldiunea: t₂=0.22 s, eta posizioa x₂= -34.26 cm
Multzoak posiziorik altuena atzematen du, ekuazioan honako baldintza betetzen denean: sin(w t+j )=+1, beraz, 8.16t+2.89=3π/2+π, eta hortik aldiunea t₃=0.61 s, eta posizioa x₃=4.86 cm

Posiziorik baxuena berriro atzematen da honako aldiune guztietan: t₂+nP, hemen P oszilazioen periodoa da eta n zenbaki osoa eta positiboa. Posiziorik altuena berriz honako aldiune guztietan atzematen da: t₃+nP.

Energiaren balantzea

Talka baino lehen

Blokea geldi dago, h=1 m altueran.

E_p=mgh

Plataforma y_e distantzia beherago dago:

E_p= -Mg·y_e

Malgukia zapalduta dago, y_edistantzia ere bai:

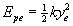
Talkaren aldiunean:

Blokearen energia potentziala energia zinetiko bilakatzen da osorik:

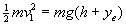
Talka inelastikoa da, beraz energia zati bat galtzen da:

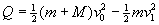
hemen v₀ da bloke-plataforma multzoaren abiadura justu talkaren ondoren.

Talkaren ondoren sistema osoaren energiak hiru zati ditu:

Bloke–plataforma multzoak energia potentzial grabitatorioa du, jatorria baino y_e distantzia beherago dago.

E_p= -(M+m)g·y_e

Energia zinetikoa

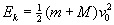
Malgukiaren energia potentzial elastikoa

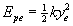
Lehen egindako adibidean:

m=10 kg, M=20 kg, k=2000 N/m. Talkaren ondorengo abiadura: v₀=1.546 m/s

eta talka gertatzen da posizio honetan: y_e=0.098 m. Energia totala:

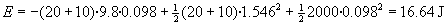
Zein posiziotan anulatzen da multzoaren abiadura: (v=0)

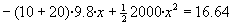
Bigarren graduko ekuazio horrek emaitza bi ematen ditu: x=0.3425 m eta x=-0.048.

Posiziorik baxuena jatorritik behera 34.25 cm dago, eta posiziorik altuena jatorritik gora 4.8 cm. Energien bidez lortutako emaitza horiek aurreko atalean ere lortu ditugu higidura ekuazioa ebatziz.

Multzoa oszilatzen ari den bitartean hiru energia-mota horien batura konstante mantentzen da, jasaten dituen indar biak kontserbakorrak direlako, grabitatea eta malgukiaren indar elastikoa.

Higiduraren ekuazio diferentziala

Blokeak eta plataformak jasaten dituzten indarrak bi dira: grabitatea eta malgukiaren indar elastikoa. Newton-en bigarren legea honela idatz daiteke:

ma= -kx -mg

(baina x≤0 denez, –kx≥0 positiboa da, irudiak erakusten duen bezala)

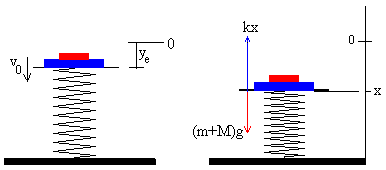
Ekuazio diferentzial gisa idazten bada:

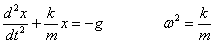
Ekuazio diferentzial horren soluzioak bi zati ditu, ekuazio homogeneoaren soluzioa eta ekuazio osoaren soluzio partikularra. Homogeneoaren soluzioa:

x₁=Asin(ωt)+Bcos(ωt)

hemen A eta B konstanteak dira eta hasierako baldintzetatik kalkula daitezke.

Ekuazio osoaren soluzio partikularra:

x₂=C

Soluzio partikularra ekuazioan ordezkatuz C konstantea kalkula daiteke:

ω²C=-g

Orduan ekuazio diferentzial osoaren soluzio osoa hau da: x=x₁+x₂

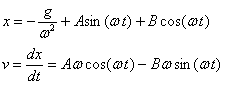
Hasierako baldintzak honakoak dira (t=0): plataforma eta blokearen hasierako posizioa x₀=-y_e eta abiadura v₀. Ekuazio bi dira eta ezezagunak A eta B.

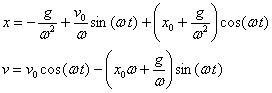
Multzoaren posiziorik baxuena eta altuena atzematen diren aldiuneak t₂ eta t₃ dira, eta bietan v=0,

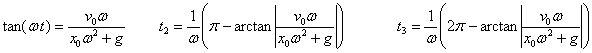
hona emaitzak:

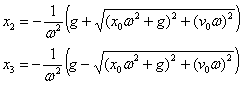
Adierazpen horiek lortzeko honako erlazio trigonometrikoak erabili dira:

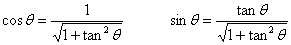
baina ωt₂ angelua bigarren koadrantekoa denez, sinua positiboa da eta kosinua negatiboa.
Eta ωt₃ angelua laugarren koadrantekoa denez, sinua negatiboa da eta kosinua positiboa.

Adibidea:

Har ditzagun berriz ere lehengo datu berak:

Blokearen masa, m=10 kg
Plataformaren masa, M=20 kg
Malgukiaren konstantea, k=2000 N/m

Blokea erortzen uzten da 1 m-ko altueratik, malgukiaren mailatik neurtuta, deformaziorik gabe.

Oreka-posizioa malgukiak gainean plataforma bakarrik duenean:

20·9.8=2000·y_e eta hortik y_e=9.8 cm

Blokearen abiadura justu talka baino lehen

Hasieran blokeak duen altuera 1.098 m, eta beraz abiadura

v₁=4.64 m/s

Blokeak plataformarekin talka egiten du:

10·4.64=(10+20)·v₀ eta hortik v₀=1.546 m/s edo 154.6 cm/s

Hasierako baldintzak

t=0, x₀=-0.098 m, v₀=1.546 m/s, eta

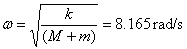
Datu guzti horiekin, higidura ekuazioa:

x=-14.7-18.94·sin(8.16·t)+4.9·cos(8.16·t) cm

Multzoaren posiziorik baxuena atzematen da aldiune honetan: t₂=0.22 s eta hemen dago x₂=-34.26 cm
Multzoaren posiziorik altuena atzematen da aldiune honetan: t₃=0.61 s eta hemen dago x₃=4.86 cm

Saiakuntza

Aukeran idatz daitezke:

Plataformaren masa, kg-tan, dagokin laukian idazten.
Blokearen masa, kg-tan, dagokion laukian idazten.
Malgukiaren konstante elastikoa (N/m-tan) dagokion laukian idazten.
Blokearen hasierako altuera finkotzat hartu da: y= 1 m=100 cm.

Berria botoia sakatu programak idatzitako datu guztiak onartzeko, eta ondoren hasi.

Esperimentuaren datuak aldatzen direnen bakoitzean berria botoia sakatu behar da.

Lehenik blokea erortzen ikusten da, gero plataformaren kontra talka inelastikoa jasaten du eta itsatsita geratzen da, azkenik multzoak oszilatu egiten du malgukiaren eraginez. Edozein unetan programa gelditu eta zehaztasunez behatzeko, Gelditu eta pausoka botoiak erabili.

Leihatilaren eskumako aldean grafikoki multzoaren posizioa erakusten da denboraren menpe oszilatzen ari direnean. Bertan grafikoan neur daitezke oszilazioen anplitudea, periodoa eta hasierako fasea.

Leihatilaren goiko aldean sistemaren energia adierazten da. Energia potentzial grabitatorioaren jatorria malgukiaren beheko muturrean hartu da, alegia ardatzaren jatorria baino 50 cm beherago. Horrela energia potentzialak beti dira positiboak eta grafikoan hobeto ikusten da nola aldatzen diren energia-mota ezberdinak euren artean eta talkaren unean galtzen den energia.

Blokea eta plataformaren energiak bi koloretako barra banaz adierazten dira: zati gorria energia potentzialari dagokio eta urdina energia zinetikoari. Barraren luzera osoak dagokion partikularen energia totala adierazten du.
Berde koloreko barrak malgukiaren energia potentzial elastikoa adierazten du.