Dinamika

Talkak

Tanke higikor batek
tiro egiten du

Erorketa askea eta
ondorengo erreboteak

Pendulu biren
arteko talkak

Aurrez-aurreko talkak
(dimentsio bakarrean)

Aurrez-aurreko
talka elastiko bi

Etengabeko talka
elastikoak
karril batean

Aurrez-aurreko
  talka bertikalak

Iraupen luzeko 
talka inelastikoa

Pendulu balistikoa

Momentu lineala
kontserbatzen ez den
pendulu balistikoa

Talka inelastikoa
malguki baten
gainean

Bala baten
abiadura neurtzea 

Bi dimentsiotako
talkak

Penduluen segida

Talka bertikal elastikoak zenbait pilotarekin

Erreferentziak

Orri honetan aurrez-aurreko talken adibide interesgarri bat deskribatzen da.

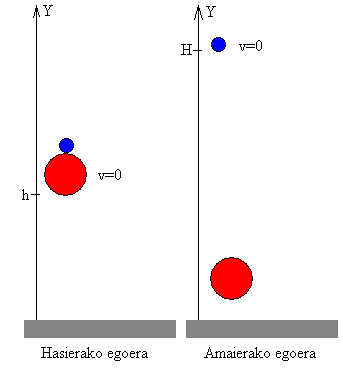
Aurreko orri batean, alegia, “Erorketa askea eta ondorengo erreboteak” izeneko orrian ikusi da, pilota bat erortzen uzten bada h0 altueratik, eta lurrean errebotea egin ostean iristen den altuera maximoa h<h0 dela. Altuera horien arteko erlazioa hau da: h=e2·h0 hemen e itzultze-koefizientea da, e≤1. Orri honetan ikusiko dugunez, pilota txiki bat pilota handiago baten gainean kokatzen bada eta biak erortzen uzten badira h0 altueratik, orduan pilota txikiak atzematen duen altuera maximoa h0 baino askoz handiagoa izan daiteke.

Pilota bi talka egiten norabide bertikalean

Pilotak partikulatzat hartuko ditugu, hau da, tamaina txikia dutela suposatuko dugu mugitzen diren distantziarekin konparatuta.

Ondoren, piloten mugimenduaren lau atalak aztertuko ditugu:

1. Pilota biak bertikalki erortzen dira

Pilota biak pausagunetik abiatzen badira, h₀ altueratik, orduan higiduraren ekuazioak honakoak dira:

v=-g·t
y=h₀-½gt²

Pilotak lurrera iristen dira y=0 denean, eta honako abiadura daukate:

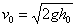
2. Pilota handiak lurraren kontra talka egiten du.
    

Pilota handiak lurraren kontra talka egin eta errebotatzen du. Itzultze-koefizientea ezagutzen bada, kalkula daiteke pilotak talkaren ondoren izango duen abiadura (u1): u1=e1v0 Hemen e1 da, pilota handiaren eta zoruaren arteko talkaren itzultze-koefizientea.

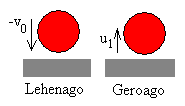
3. Pilota txikiak eta handiak aurrez-aurre talka egiten dute
    

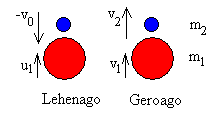Alboko irudiak erakusten duen bezalaxe, pilota handiak m1 masa du eta u1 abiadura gorantz; pilota txikiak ordea, m2 masa du eta u2 abiadura beherantz, baina hain zuzen ere, u2=-v0 eta baldintza horietan aurrez-aurreko talka jasaten dute.

Talkaren ondorengo bi abiadurak kalkulatzeko (v₁ eta v₂) aplika dezagun:

• Momentu linealaren kontserbazio printzipioa

m₁·u₁+m₂(-v₀)=m₁·v₁+m₂·v₂

• Eta itzultze-koefizientearen definizioa:

v₁-v₂=-e₂(u₁-(-v₀))

Hemen e₂ da, pilota handiaren eta txikiaren arteko talkaren itzultze-koefizientea.

Kalkuluak erraztearren har ditzagun bi itzultze koefizienteak berdinak: e₁≈e₂=e

m₁ev₀-m₂v₀=m₁·v₁+m₂·v₂
v₁-v₂=-e(ev₀+v₀)

Bi ekuaziodun sistema horretan bi ezezagunak dira, v₁ eta v₂, izan ere piloten abiadurak talkaren ondoren:

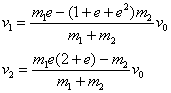
4. Pilota biak bertikalki gorantz igotzen dute:

Pilotek gorantz igotzen dute, baina bakoitzak hasierako abiadura ezberdina du, beraz altuera ezberdinak atzemango dituzte. Pilota handia v₁ abiaduraz abiatzen da gorantz eta pilota txikia v₂ abiaduraz. Lehenengoaren higiduraren ekuazioak:

v=v₁-g·t
y=v₁·t -½gt²

Eta altuera maximoa atzematen duenean: v=0.

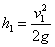
Bigarren pilotak ere ekuazio analogoak ditu, baina "bat" azpindizearen ordez "bi".
 

Kasu bereziak

1. Pilota handia, justu pilota txikiarekin talka egin ondoren, geldi geratzea: v₁=0

Esaterako, talka elastikoak badira, e=1, orduan v₁=0 baldintza lortzen da honako masa erlazioarekin: m₁=3m₂. Beraz, kasu horretan pilota handia justu pilota txikiaren kontra talka egin ondoren geldi geratzen da lurrean, bere masa txikiarenaren hirukoitza bada. Orduan pilota txikiaren abiadura v₂=2v₀, eta atzematen duen altuera maximoa hau da: h₂=4h₀

Orokorrean, pilota txikiak atzematen duen altuera maximoa hasierakoa baino handiagoa izan dadin (h₂>h₀) abiadura handiagoa izan behar du talkaren ondoren, (v₂>v₀) eta atzeman dezakeen altuera handiena lortzen da v₁=0 gertatzen denean, alegia pilota handia lurrean geldi geratzen denean.

Bigarren ekuazioan (itzultze-koefizientearen definizioan) ordezkatzen bada v₁=0, orduan v₂>v₀ lortzeko, honako baldintza bete behar da: e²+e-1>0, hau da, e>0.618.

Eta pilota handia lurrean geldi geratzeko (v₁=0) masen arteko erlazioak (m₁/m₂) honako baldintza bete behar du (itzultze koefizientea edozein izanik ere e>0.618):

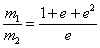
Esaterako, har ditzagun honako balioak: e=0.9 eta m₁=3.011·m₂ (pilota handiaren m₁ masa pilota txikiaren hirukoitza baino pixka bat handiagoa da): orduan pilota txikiaren abiadura v₂=1.71v₀, eta beraz, h₂=2.92·h₀

2. Pilota txikiaren masa arbuiagarria bada

Pilota txikiaren masa arbuiagarria bada, m₂<<m₁, eta talka elastikoetan, e=1, orduan honako abiadura lortzen da v₂≈3·v₀, hortaz, pilota txikiak atzematen duen altuera maximoa hau da h₂≈9·h₀.

Energiaren balantzea

• Piloten energia hasieran lurretik h₀ altueran eta pausagunean daudenean:

E_i=(m₁+m₂)gh₀

• Pilota handiak zoruaren kontra talka egiten du eta energiaren zati bat galtzen du: Q₁. Talka baino lehenagoko abiadura v₀ da eta talkaren ondorengoa e·v₀.

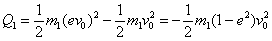
• Pilota txikia lurrera iristen da v₀ abiaduraz, eta pilota handiaren kontra talka egiten du, baina pilota handiak, zoruaren kontra talka egin ondoren, goranzko abiadura du: ev₀. Bigarren talka horretan ere energia galtzen da, 

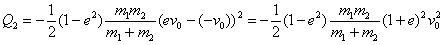
• Amaieran, soberan geratzen den energia E_f=E_i+Q₁+Q₂  (Q₁ eta Q₂ negatiboak dira) pilota bien energia zinetikoen batura da, eta gorantz abiatzen dira v₁ eta v₂ abiadurez.
   

• Geroago energia zinetiko hori, energia potentzial bilakatzen da, pilotek altuera maximoak atzematen dituztenean: h₁ eta h₂ .

Pilota handia zoruan geldi geratzen bada, v₁=0, orduan amaierako energia, E_f , osorik bilakatzen da pilota txikiaren energia potentzial, bere h₂ altuera maximoa atzematen duenean.

Adibidea

Demagun e=0.9 eta m₁=3.011·m₂, Hasierako altuera h₀=0.25 m

1. Hasierako energia E_i=4.011·9.8·0.25= 9.83 J
2. Pilota handiaren abiadura lurrera iristean: v₀=2.21 m/s.
3. Zoruaren kontra talka egin ondorengo abiadura: e·v₀=1.99 m/s. Talkan galdutako energia: Q₁=-1.40 J
4. Pilota txikia lurrera iristen da abiadura berberaz: v₀=2.21 m/s eta pilota handiaren kontra talka egiten du. Galdutako energia: Q₂=-1.26 J
5. Pilota handia lurrean geldi geratzen da, beraz, pilota txikiaren energia zinetikoa: E_f=9.83-1.40-1.26=7.16 J. Energia zinetiko hori galtzen doa pilota txikia igotzen den heinean, energia potentziala handitzen doalako, eta azkenean atzematen duen altuera maximoa: h₂=0.73 m.

Saiakuntza

• Pilota txikiaren masa finkotzat hartu da: m₂=1 kg.

Aukeran idatz daitezke:

• Pilota handiaren masa, m₁ , masa handia laukian (bat baino handiagoa izan behar da).
• Itzultze-koefizientea, e, zenbaki bat aukeratuz 0.6 eta 1.0 bitartean.
• Hasierako altuera, h₀, zentimetrotan, desplazamendu-barrari saguaz eragiten.

Hasi botoia sakatu.

Esate baterako:

• Masa handia, m₁=200,
• Itzultze-koefizientea, e=1.0,
• Hasierako altuera, h₀=10 cm.

Pilota txikiak azkenean atzematen duen altuera maximoa h₂ ≈ 90 cm

Alda bedi itzultze-koefizientea, e, eta bila bedi pilota handiaren m₁ masaren balioa, lurrean geldi uzten duena pilota txikiarekin talka egin ondoren.

• Leihatilaren ezkerreko aldean bi pilotak bertikalki mugitzen ikusten dira, handia gorriz eta txikia urdinez.

• Erdi aldeko barrek piloten energia adierazten dute (zinetikoa gehi potentziala) eta nola ari den aldatzen.

• Eskumako aldean pilota txikiaren abiadura grafikoki adierazten da denboraren menpe.

Talka bertikal elastikoak zenbait pilotarekin

Atal honetan talka bertikal elastikoak aztertuko ditugu bi eta hiru pilotekin, eta ondoren emaitza orokortuko dugu n piloten kasurako.

Bi pilota

1. Pilota bi, azpikoak m₁ eta gainekoak m₂, erortzen ari dira elkarrekin h₀ altueratik abiatuta eta lurrera iristen direnean -v₀ abiadura dute.

2. Azpiko pilotak (m₁) lurraren kontra elastikoki talka egiten du eta bere abiaduraren noranzkoa aldatzen du baina modulua ez.

3. Gaineko pilotak (m₂ masa eta –v₀ abiaduraz) azpiko pilotarekin talka egiten du (m₁ masa eta v₀ abiadura). Talkaren ondoren pilota bien abiadurak v₁ eta v₂ dira.

• Momentu linealaren kontserbazio printzipioa

m₁·v₀+m₂(-v₀)=m₁·v₁+m₂·v₂

• Itzultze-koefizientearen definizioa

v₁-v₂=-e(v₀-(-v₀))

Eta talka elastikoa bada, e=1

v₁-v₂=-2v₀

Ekuazio biko sistema horretan bi ezezagunak bakan daitezke: v₁ eta v₂.

• Baldin m₁=m₂, bada orduan, v₂=v₀

• Baldin m₁=3m₂, bada orduan, v₂=2v₀

• Baldin m₁>>m₂ bada orduan, v₂=3v₀

Pilota txikiak atzematen duen altuera maximoa hau da: h=9·h₀

Hiru pilota

1. Hiru pilota, azpikoa m₁, erdikoa m₂ eta gainekoa m₃, erortzen ari dira elkarrekin h₀ altueratik abiatuta, eta lurreraino iristen direnean -v₀ abiadura dute.

2. Azpiko pilotak lurrarekin talka elastikoa jasaten du eta bere abiaduraren noranzkoa aldatzen du baina modulua ez.

3. Erdiko pilotak (m₂ masa eta –v₀ abiaduraz) azpiko pilotarekin talka egiten du (m₁ masa eta v₀ abiadura). Talkaren ondoren pilota bien abiadurak v₁ eta v₂ dira.

Momentu linealaren kontserbazioa aplikatuz eta talka elastikoa dela suposatuz: m₁·v₀+m₂(-v₀)=m₁·v₁+m₂·v₂
v₁-v₂=-2v₀

Lehen bezala, bi ekuazioko sistematik bi ezezagunak bakan daitezke: v₁ eta v₂.

4. Gaineko pilotak (m₃ masa eta –v₀ abiaduraz) erdiko pilotarekin talka egiten du (m₂ masa eta v₂ abiadura). Talkaren ondoren pilota bien abiadurak V₂ eta v₃ dira.

Momentu linealaren kontserbazioa aplikatuz eta talka elastikoa dela suposatuz: m₂·v₂+m₃(-v₀)=m₂·V₂+m₃·v₃
V₂-v₃=-(v₂-(-v₀))

Lehen bezala, bi ekuazioko sistematik bi ezezagunak bakan daitezke: v₃ eta V₂.

• Baldin m₁=m₂=m₃ orduan, v₃=v₀

• Baldin m₁>>m₂>>m₃ orduan, v₃=7v₀

Gaineko pilotak atzematen duen altuera maximoa hau da: h=49·h₀

Lau pilota

Baldin m₁>>m₂>>m₃>>m₄ orduan, v₄=15v₀

Gaineko pilotak atzematen duen altuera maximoa hau da: h=225·h₀

n pilota

Baldin m₁>>m₂…. >>m_n orduan, v_n=(2ⁿ-1)v₀

Esate baterako, 100 metroko altuerako eraikin batetik zortzi pilota erortzen uzten baditugu elkarrekin, lurreraino iristean izango duten abiadura honakoa izango da:

Eta pilota guztien masek honako baldintza betetzen badute:

m₁>>m₂>>… >>m₈

Orduan gaineko pilotak atzematen duen abiadura talkaren ondoren:

v₈=(2⁸-1)v₀=11289.3 m/s

Izan ere, abiadura hori Lurraren gainazaleko ihes abiadura baino altuagoa da.

R=6370 km  Lurraren erradioa da, M=5.98·10²⁴ kg Lurraren masa eta G=6.67·10^-11 N·m²/kg² grabitazio unibertsalaren konstantea.