Dinamika

Talkak

Tanke higikor batek
tiro egiten du

Erorketa askea eta
ondorengo erreboteak

Pendulu biren
  arteko talkak

Aurrez-aurreko talkak
(dimentsio bakarrean)

Aurrez-aurreko
talka elastiko bi

Etengabeko talka
elastikoak 
karril batean

Aurrez-aurreko
talka bertikalak

Iraupen luzeko 
talka inelastikoa

Pendulu balistikoa

Momentu lineala
kontserbatzen ez den
pendulu balistikoa

Talka inelastikoa
malguki baten
gainean

Bala baten
abiadura neurtzea 

Bi dimentsiotako
talkak

Penduluen segida

Oinarri fisikoak

Ondorengo talkak pendulu bien artean

Saiakuntza

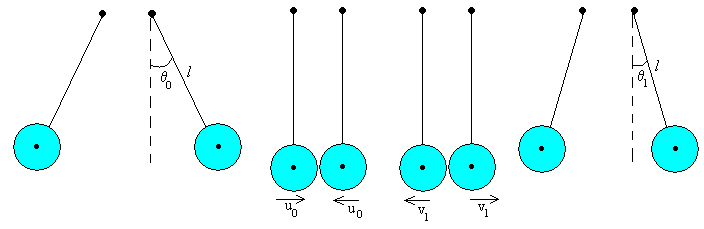
Esfera identiko bi hari banatan eskegitzen dira baina elkarri ukitzen, ondorengo irudiak erakusten duen bezala. Esferak oreka posiziotik ateratzen dira (biak angelu bera baina aurkako noranzkoaz) eta askatu egiten dira. Hariek ez dute ia masarik eta ez dira elastikoak.

Esferek erdian topo egiten dute eta errebotatu. Berriro igo, simetrikoki, eta berriro talka, behin eta berriz. Denboran zehar, talken ondorioz, higiduraren anplitudea gutxituz joango da.

Oinarri fisikoak

Penduluen higidura

Esfera bakoitzaren higidura penduluarena da, alegia, l luzeradun hari zurrun batean m masadun partikula bat eskegita. Hona hemen higiduraren ekuazioa: m·at= -mg·sinθ

Ekuazio diferentzial horren soluzioa da, θ posizio angeluarra denboraren menpe (pendulu bakoitzarena bertikalarekiko). Ez dugu egingo angelu txikien hurbilketa, beraz, ekuazio diferentzial hori ebazteko prozedura numerikoak erabili behar dira, eta hasierako baldintzak:

• Goranzkoan: hasiera θ=0 posizioan, eta dθ/dt=v/l, abiadura angeluarraz. Hemen v esferaren abiadura da talkaren ondoren.
• Beheranzkoan: hasiera θ=θ₀ posizioan, alegia desplazamendu maximoa, eta abiadura angeluarra: dθ/dt=0

Energiaren balantzea

Konpara ditzagun penduluaren posizio bi:

Muturreko posizioan, θ=θ0, energia potentziala soilik du: E=mg(l-l·cosθ0) Eta bitarteko θ posizio batean energiak bi zati ditu, zinetikoa eta potentziala:

Energia kontserbatu egiten da:

v²=2gl(cosθ-cosθ₀)

Hortaz, esferen abiadura, justu talka egitera doazen unean hau da (θ=0):

u²=2gl(1-cosθ₀)

Esfera bien arteko talka

Itzultze koefizientearen definizioak erlazionatzen ditu esferen abiadurak talkaren ondoren (v₁=-v eta v₂=v) eta talka baino lehen (u₁=u eta u₂=-u):

v₁-v₂= -e(u₁-u₂)
-2v= -e(2u), 

Esferen abiadura, v, gutxitu egiten da talkaren ondorioz, itzultze koefizientea beti delako e<1.

v=e·u

Ondorengo talkak pendulu bien artean

Ondorengo irudiak lau egoera erakusten ditu:

• Hasierako posizioa, abiadura angeluarra nulua denean.
• Esfera biak justu talka egin baino lehen.
• Esfera biak justu talka burutu ondoren.
• Amaierako posizioa, gehienez urrundu eta gelditzen diren tokian.

• Lehen talka

Hasierako aldiunean, t=0, esferak pausagunean daude eta bertikalarekiko θ₀ posizioan. Mugitzean, hurbiltzen doaz eta justu talka egiten dute θ=0 posizioan. Une horretan duten abiadura u₀ da.

Eta talkaren ondoren esferek honako abiadura dute (v₁):

v₁=e·u₀

Talkaren ondoren esferak berriro urruntzen dira desbiazio maximoa atzematen duten arte: θ₁

Desbiazio maximoak, θ₀ hasieran eta θ₁ amaieran, honela erlazionatuta daude:

cosθ₁=1-e²+e²·cos θ₀

• Bigarren talka

Esferek bigarren talka egitera doazen unean u₁ abiadura dute, justu lehen talkaren ondoren zeukaten berbera: v₁, bitarte horretan energia kontserbatu delako:

u₁=v₁

Eta bigarren talkaren ondoren esferek duten abiadura, v₂, itzultze koefizientearen bitartez erlazionatzen da:

v₂=e·u₁

Ondoren, esferak urrundu egingo dira, berriro desbiazio maximoa atzeman arte: θ₂

Desbiazio maximoak, θ₁ hasieran eta θ₂ amaieran, honela erlazionatuta daude:

cosθ₂=1-e²+ e²·cos θ₁
cosθ₂=1-e⁴+ e⁴·cos θ₀

• n-garren talka

Har ditzagun desbiazio maximoko angelu bi, θ_n eta θ_n-1. Hona hemen bien arteko erlazioa:

cosθ_n=1-e²+ e²·cos θ_n-1

Eta hortik deduzi daiteke, azkenekoaren (θ_n) eta lehenengoaren (θ₀) arteko erlazioa:

cosθn=1-e2n+ e2n·cos θ0

Angeluekin jokatu beharrean erosoagoa izaten da bere proiekzio horizontala behatzea: x_n  (X ardatzean).

x_n=l·sinθ_n

Energiaren balantzea

Esferek talkak errepikatzen dituzten heinean energia galduz doaz. Esferen hasierako energia hau da:

E₀=mg(l-l·cosθ₀)

Eta n talkaren ondoren geratzen zaien energia:

E_n=mg(l-l·cosθ_n)=mgl·e²ⁿ·(1-cosθ₀)

Adibidea

Demagun esfera biak oreka posiziotik ateratzen ditugula, θ₀=90º posizioraino.

Ondorengo taulak erakusten du (e=0.8 kasurako) lehen bost talketan zein den desbiazio maximoa, θ_n, posizio horren projekzio horizontala, x_n, eta energia, E_n.

Saiakuntza

Aukeran idatz daiteke:

• Itzultze-koefizientea, e, desplazamendu barrari saguaz eragiten.

Hasi botoia sakatu.

Bi esferak identikoak dira eta θ₀=90º posiziotik abiatzen dira.

Esferak jaitsi, hurbildu eta talka egiten dute aurrez-aurre. Ondoren urrundu eta abiadura galtzen doaz desbiazio maximoa atzematen duten arte. Horrela behin eta berriz jarraitzen dute guztiz gelditu arte.

Esferak desbiazio maximora iristen diren bakoitzean, ardatz horizontalean projekzioa markatzen da.

Leihatilaren ezkerreko aldean energiaren balantzea erakusten da:

• Energia zinetikoa (urdinez), energia potentziala (gorriz) eta bien batura.

• Hasierako energia totala lauki beltz batez adierazten da.

Leihatilaren goiko aldean honako datuak erakusten dira:

• Penduluek bertikalarekin osatzen duten angelua.

• Esferen abiadura angeluarra, izan ere, desbiazio maximoa atzematen den unean nulua da.

• Geratzen den energia totalaren proportzioa hasierako energiarekiko: E/E₀.