Choque de las moléculas de un gas con un émbolo móvil

El número de moléculas cuya velocidad está comprendida entre v y v+dv, es decir, entre v_x y v_x+dv_x, v_y y v_y+dv_y, v_z y v_z+dv_z, de acuerdo a la ley de Boltzmann es

${\displaystyle dn=N{\left(\frac{m}{2\pi kT}\right)}^{3/2}\exp \left(-\frac{m{v}^2}{2kT}\right)dv}$

donde dv es un elemento de volumen en el espacio de las velocidades.

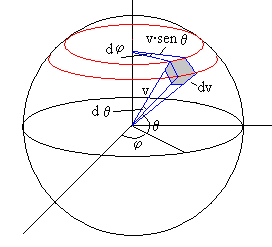
Expresamos el elemento de volumen dv en el espacio de velocidades en coordenadas polares. Para ello,

• Trazamos dos esferas concéntricas de radio v y v+dv.

• Cortamos las esferas por dos planos meridianos que pasan por los ángulos φ y φ+dφ.

• Cortamos las esferas por dos planos paralelos de ángulos θ, y θ+dθ

El volumen comprendido es paralepípedo elemental de color gris de la figura tiene por lados

dv, v·sinθ·dφ, v·dθ

Su volumen es

dv=v²·sinθ·dv·dθ·dφ

Número de moléculas del gas que chocan con el émbolo

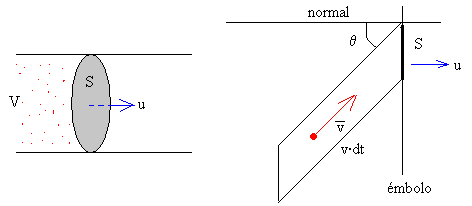
El número de moléculas con velocidad v que chocan contra una porción de émbolo de área S en el tiempo dt, que se mueven en una dirección que hace un ángulo θ con la normal a la pared, son las contenidas en el volumen cilíndrico de base S y altura v·cosθ·dt. Se multiplica el número de moléculas por unidad de volumen (dn/V) por el volumen del cilindro de la figura de la derecha.

(dn/V)·S·v·cosθ·dt.

Ahora bien, el émbolo no está en reposo, sino que se mueve con velocidad u a lo largo de la dirección normal a S. La componente de la velocidad de las moléculas con relación al émbolo es v·cosθ-u. Donde u es positiva cuando el gas incrementa su volumen y negativa cuando lo disminuye. Se supone que u es pequeña comparada con las velocidades moleculares v.

El número de moléculas del gas que chocan con el émbolo en el intervalo de tiempo comprendido entre t y t+dt es

${\displaystyle \frac{1}{V}{\displaystyle \int (v·\cos \theta -u)·S·dt·dn=}\frac{dV}{V}\frac{1}{u}{\displaystyle \int (v·\cos \theta -u)·dn}}$

donde dV=S·u·dt es el incremento del volumen del gas

Choque elástico de una molécula con el émbolo

Una partícula de masa m y velocidad v_x choca elásticamente con un émbolo de masa M que se mueve con velocidad u.

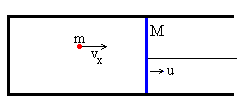
Aplicamos la conservación del momento lineal y la igualdad de la energía cinética antes y después del choque

${\displaystyle \begin{array}{l}m{v}_x+Mu=m{v}_x^{\text{'}}+Mu\text{'}\\ \frac{1}{2}m{\left(v_x\right)}^2+\frac{1}{2}M{u}^2=\frac{1}{2}m{\left(v_x^{\text{'}}\right)}^2+\frac{1}{2}M{\left(u\text{'}\right)}^2\end{array}}$

Escribimos las dos ecuaciones en la forma equivalente

${\displaystyle \begin{array}{l}m(v_x-v_x^{\text{'}})=M(u\text{'}-u)\\ m(v_x-v_x^{\text{'}})(v_x+v_x^{\text{'}})=M(u\text{'}-u)(u\text{'}+u)\end{array}}$

Despejando las incógnitas

${\displaystyle \begin{array}{l}{v}_x^{\text{'}}=\frac{2Mu+(m-M)v_x}{m+M}u\text{'}=\frac{2m{v}_x+(M-m)u}{m+M}\\ v_x^{\text{'}}=\frac{2u+(m/M-1)v_x}{m/M+1}u\text{'}=\frac{2(m/M)v_x+(1-m/M)u}{m/M+1}\end{array}}$

Como la masa M del émbolo es muy grande comparado con masa m de la partícula

${\displaystyle v_x^{\text{'}}=2u-v_{x}u\text{'}=u}$

Una deducción alternativa es la siguiente:

La partícula choca con el émbolo y cambia el sentido de su velocidad en el Sistema de Referencia del émbolo, la velocidad de la partícula

• Antes del choque es (vcosθ-u)
• Después del choque es -(vcosθ-u)

En el Sistema de Referencia del Laboratorio, las velocidades de la partícula

• Antes del choque es (vcosθ-u)+u= vcosθ
• Después del choque es -(vcosθ-u)+u=2u-vcosθ

Variación de la energía interna del gas ideal

El cambio de energía cinética de la partícula es

$$\begin{gathered} {\displaystyle \Delta E_k=\frac{1}{2}m\left({(2u-v\cos \theta )}^2+v_y^2+v_z^2\right)-\frac{1}{2}m\left({(v\cos \theta )}^2+v_y^2+v_z^2\right)= \\ 2mu(u-v\cos \theta )} \end{gathered}$$

Las moléculas cuando chocan con el émbolo ganan o pierden energía cinética. Si ganan energía cinética, la energía interna del gas aumenta y también lo hace la temperatura y si pierden, la energía interna del gas disminuye.

Vamos a calcular el cambio de energía interna debido a todos los choques de las N moléculas del gas con el émbolo móvil en el intervalo de tiempo comprendido entre t y t+dt o bien, cuando el volumen del gas cambia de V a V+dV.

${\displaystyle \begin{array}{l}dU=\frac{dV}{V}\frac{1}{u}{\displaystyle \int 2mu(u-v\cos \theta )(v·\cos \theta -u)·dn=}\\ -2m\frac{dV}{V}N{\left(\frac{m}{2\pi kT}\right)}^{3/2}{\displaystyle \underset{0}{\overset{\infty }{\int }}{\displaystyle \underset{0}{\overset{\pi /2}{\int }}{\displaystyle \underset{0}{\overset{2\pi }{\int }}\exp \left(-\frac{m{v}^2}{2kT}\right)}}}{\left(u-v·\cos \theta \right)}^2·v^2\sin \theta ·dv·d\theta ·d\phi \end{array}}$

Para calcular la integral triple, establecemos los límites de integración para la variable v, φ y θ.

Los límites de la primera integral respecto de φ, son 0 y 2π, se integra para todos los ángulos, pero solamente se integra para ángulos θ comprendidos entre 0 y π/2, ya que cuando θ>π/2, v·cosθ se hace negativa y la partícula se aleja de la pared. Por último, se integra para todas las velocidades, desde 0 a ∞.

${\displaystyle \begin{array}{l}dU=-4\pi m\frac{dV}{V}N{\left(\frac{m}{2\pi kT}\right)}^{3/2}{\displaystyle \underset{0}{\overset{\infty }{\int }}{\displaystyle \underset{0}{\overset{\pi /2}{\int }}\exp \left(-\frac{m{v}^2}{2kT}\right)(u^2{v}^2-2u{v}^3·\cos \theta +v^4{\cos }^2\theta )\sin \theta ·dv·d\theta }}\\ =-4\pi m\frac{dV}{V}N{\left(\frac{m}{2\pi kT}\right)}^{3/2}{\displaystyle \underset{0}{\overset{\infty }{\int }}\exp \left(-\frac{m{v}^2}{2kT}\right)}(u^2{v}^2-u{v}^3+\frac{1}{3}{v}^4)dv\end{array}}$

Empleando los resultados de las integrales

${\displaystyle \begin{array}{l}{\displaystyle \underset{0}{\overset{\infty }{\int }}{x}^2\exp (-\alpha x^2)}=\frac{1}{4}\sqrt{\frac{\pi }{{\alpha }^3}}\\ {\displaystyle \underset{0}{\overset{\infty }{\int }}{x}^3\exp (-\alpha x^2)}=\frac{1}{2{\alpha }^2}\\ {\displaystyle \underset{0}{\overset{\infty }{\int }}{x}^4\exp (-\alpha x^2)}=\frac{3}{8}\sqrt{\frac{\pi }{{\alpha }^5}}\end{array}}$

>> syms x;
>> syms a positive;
>> int('x^2*exp(-a*x^2)',x,0,inf)
ans =pi^(1/2)/(4*a^(3/2))
>> int('x^3*exp(-a*x^2)',x,0,inf)
ans =1/(2*a^2)
>> int('x^4*exp(-a*x^2)',x,0,inf)
ans =(3*pi^(1/2))/(8*a^(5/2))

Llegamos a la siguiente expresión

${\displaystyle \begin{array}{l}dU=-4\pi m\frac{dV}{V}N{\left(\frac{m}{2\pi kT}\right)}^{3/2}\left\{u^2\frac{\sqrt{\pi }}{4}{\left(\frac{2kT}{m}\right)}^{3/2}-u\frac{1}{2}{\left(\frac{2kT}{m}\right)}^2+\frac{\sqrt{\pi }}{8}{\left(\frac{2kT}{m}\right)}^{5/2}\right\}=\\ -mN\frac{dV}{V}\left\{u^2-\frac{2}{\sqrt{\pi }}u{\left(\frac{2kT}{m}\right)}^{1/2}+\frac{1}{2}\left(\frac{2kT}{m}\right)\right\}\end{array}}$

La presión del gas en el émbolo

El gas está adibáticamente aislado por lo que la variación de energía interna es igual al trabajo realizado (cambiado de signo) dU=-p_e·dV. Ya que cuando el gas realiza un trabajo su energía interna disminuye

${\displaystyle p_e=\frac{mN}{V}\left\{u^2-u\sqrt{\frac{8kT}{\pi m}}+\frac{kT}{m}\right\}}$

La presión de un gas p₀ en equilibrio, contenido en un recipiente de volumen V a la temperarura T es p₀=NkT/V

Expresamos p_e/p₀ en términos del cociente α=u/<v>, siendo <v> la velocidad media de las moléculas del gas

${\displaystyle <v>=\sqrt{\frac{8kT}{\pi m}}}$

Representamos p_e/p₀ en función de α

${\displaystyle \frac{p_e}{p_0}=1-\frac{8}{\pi }\alpha +\frac{8}{\pi }{\alpha }^2}$

p=@(x) 1-8*x/pi+8*x.^2/pi;
fplot(p,[-0.5,0.5])
grid on
ylim([0,2.5])
xlabel('\alpha')
ylabel('p_e/p_0')
title('Presión')

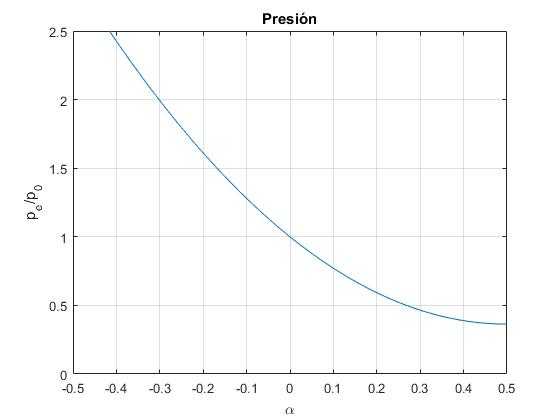
Debido al movimiento del émbolo, la presión del gas en el émbolo es distinta de la presión del mismo gas en equilibrio a la misma temperatura

La temperatura del gas

La variación de energía interna de un gas es dU=nc_v·dT. Donde c_v es el calor específico a volumen constante del gas, n el número de moles y dT la variación de temperatura

${\displaystyle n{c}_{v}dT=-mN\frac{dV}{V}\left\{u^2-u\sqrt{\frac{8kT}{\pi m}}+\frac{kT}{m}\right\}}$

Si la velocidad u del émbolo es constante, podemos integrar esta ecuación diferencial

${\displaystyle {\displaystyle \underset{T_0}{\overset{T}{\int }}\frac{dT}{\left\{u^2-u\sqrt{\frac{8kT}{\pi m}}+\frac{kT}{m}\right\}}}=-\frac{mN}{n{c}_v}{\displaystyle \underset{V_0}{\overset{V}{\int }}\frac{dV}{V}}}$

Haciendo el cambio de variable x²=T

${\displaystyle {\displaystyle \underset{T_0}{\overset{T}{\int }}\frac{2xdx}{\left(\frac{m}{k}{u}^2-u\sqrt{\frac{8m}{\pi k}}x+x^2\right)}}=-\frac{R}{c_v}{\displaystyle \underset{V_0}{\overset{V}{\int }}\frac{dV}{V}}}$

La integral de la derecha es inmediata, la de la izquierda es del tipo

${\displaystyle \begin{array}{l}{\displaystyle \int \frac{2x}{x^2-bx+c}}dx={\displaystyle \int \frac{2x-b}{x^2-bx+c}}dx+{\displaystyle \int \frac{b}{x^2-bx+c}}dx=\\ \log \left(x^2-bx+c\right)+\frac{b}{\sqrt{c-b^2/4}}\arctan \left(\frac{x-b/2}{\sqrt{c-b^2/4}}\right)\end{array}}$

El integrando del primer miembro es la función f(T)

${\displaystyle f(T)=\log \left(T-u\sqrt{\frac{8m}{\pi k}T}+\frac{m}{k}{u}^2\right)+\frac{2}{\sqrt{\pi /2-1}}\arctan \left(\frac{\sqrt{T}-u\sqrt{\frac{2m}{\pi k}}}{u\sqrt{\frac{m}{k}}\left(1-\frac{2}{\pi }\right)}\right)}$

La ecuación que relaciona el volumen V y la temperatura T del gas es

${\displaystyle f(T)-f(T_0)=-\frac{R}{c_v}\log \left(\frac{V}{V_0}\right)}$

Ecuaciones del movimiento

Definimos nuevas variables:

• nM_g=mN es la masa del gas (m es la masa de una molécula y N es el número de moléculas contenidas en el volumen V del gas, n es el número de moles, M_g es la masa de un mol). Para un mol de gas, N es el número de Avogadro, N·k=R=8.3143 J/(K·mol)

• u=dx/dt es la velocidad del émbolo (x es la posición del émbolo)

• V=S·x es el volumen del gas

• El cambio infinitesimal de volumen del gas es dV=S·dx=S·(dx/dt)dt

• dU=n·c_v·dT, es la variación de energía interna de n moles de gas ideal. c_v es el calor específico molar a volumen constante.

Escribimos la ecuación que describe la variación de la temperatura del gas en términos de las nuevas variables

${\displaystyle c_v\frac{dT}{dt}=-\frac{RT}{x}\left(\frac{dx}{dt}\right)+\sqrt{\frac{8R{M}_g}{\pi }}\frac{\sqrt{T}}{x}{\left(\frac{dx}{dt}\right)}^2-\frac{M_g}{x}{\left(\frac{dx}{dt}\right)}^3}$

Escribimos la presión del gas en el émbolo, en términos de las nuevas variables

${\displaystyle p_e=\frac{n}{Sx}\left\{M_g{\left(\frac{dx}{dt}\right)}^2-\sqrt{\frac{8R{M}_{g}T}{\pi }}\left(\frac{dx}{dt}\right)+RT\right\}}$

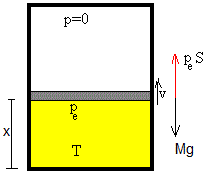
Sobre el émbolo actúan dos fuerzas, su peso Mg y la fuerza que ejerce la presión del gas p_eS

${\displaystyle \begin{array}{l}M\frac{d^{2}x}{d{t}^2}=p_{e}S-Mg\\ \frac{d^{2}x}{d{t}^2}=\frac{n}{Mx}\left\{M_g{\left(\frac{dx}{dt}\right)}^2-\sqrt{\frac{8R{M}_{g}T}{\pi }}\left(\frac{dx}{dt}\right)+RT\right\}-g\end{array}}$

Tenemos que resolver un sistema de dos ecuaciones diferenciales, con las siguientes condiciones iniciales: en el instante t=0, la posición del émbolo es x₀, su velocidad es dx/dt=0, y la temperatura del gas es uniforme e igual a T₀

Variables adimensionales

Escribimos las dos ecuaciones diferenciales en términos de las siguientes variables adimensionales: θ temperatura, ξ desplazamiento, τ tiempo, y los siguientes parámetros: γ índice adiabático del gas, μ gravedad adimensional y δ (raíz cuadrada del cociente: masa de un mol de gas M_g, masa del émbolo M)

${\displaystyle \begin{array}{l}\tau =\frac{t}{\sqrt{\frac{M{L}^2}{R{T}_0}}}\theta =\frac{T}{T_0}\xi =\frac{x}{L}\\ \gamma =\frac{c_p}{c_v}\delta =\sqrt{\frac{8M_g}{\pi M}}\mu =g\frac{ML}{R{T}_0}\end{array}}$

Resolvemos el sistema de ecuaciones diferenciales con las condiciones iniciales: en el instante τ=0, la temperatura del gas es θ₀ para la posición ξ₀ del émbolo, que parte del reposo, dξ/dτ=0

${\displaystyle \begin{array}{l}\frac{d\theta }{d\tau }=-\left(\gamma -1\right)\frac{\theta }{\xi }\left(\frac{d\xi }{d\tau }\right)+\left(\gamma -1\right)\delta \frac{\sqrt{\theta }}{\xi }{\left(\frac{d\xi }{d\tau }\right)}^2-\left(\gamma -1\right)\frac{\pi {\delta }^2}{8}\frac{1}{\xi }{\left(\frac{d\xi }{d\tau }\right)}^3\\ \frac{d^2\xi }{d{\tau }^2}=n\left\{\frac{\pi {\delta }^2}{8}\frac{1}{\xi }{\left(\frac{d\xi }{d\tau }\right)}^2-\delta \frac{\sqrt{\theta }}{\xi }\left(\frac{d\xi }{d\tau }\right)+\frac{\theta }{\xi }\right\}-\mu \end{array}}$

Energía del sistema

La energía del sistema aislado formado por el gas y el émbolo, se compone de tres términos:

• La energía potencial del émbolo
• La energía cinética del émbolo
• la energía interna del gas ideal

${\displaystyle \frac{1}{2}M{\left(\frac{dx}{dt}\right)}^2+Mgx+n{c}_{v}T=\text{cte}}$

Expresado en términos de las variables adimensionales definidas en el aprtado anterior

${\displaystyle \frac{1}{2}\left(\gamma -1\right){\left(\frac{d\xi }{d\tau }\right)}^2+\mu \left(\gamma -1\right)\xi +n\theta =\mu \left(\gamma -1\right){\xi }_0+n{\theta }_0}$

El segundo miembro es la energía inicial del sistema con el émbolo en reposo

Estado final

En el estado final, la velocidad dξ/dτ=0 y la aceleración d²ξ/dτ²=0 del émbolo es nula. La ecuación del movimiento del émbolo se convierte en (la segunda línea es la misma que la primera pero expresada en términos de variables adimensionales)

${\displaystyle \begin{array}{l}\frac{nR{T}_f}{M{x}_f}-g=0\\ n{\theta }_f=\mu {\xi }_f\end{array}}$

La conservación de la energía entre el estado inicial y final se escribe (la segunda línea es la misma que la primera pero expresada en términos de variables adimensionales)

${\displaystyle \begin{array}{l}Mg{x}_f+n{c}_v{T}_f=Mg{x}_0+n{c}_v{T}_0\\ \mu \left(\gamma -1\right){\xi }_f+n{\theta }_f=\mu \left(\gamma -1\right){\xi }_0+n{\theta }_0\end{array}}$

Resultados

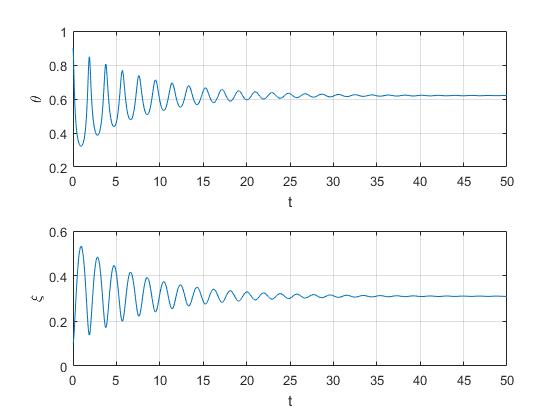
Resolvemos, empleando procedimientos numéricos, el sistema de ecuaciones diferenciales, con los valores que se especifican para los parámetros y con las condiciones iniciales: Posición del émbolo ξ₀=0.1, temperatura inicial θ=0.9. Representamos la temperatura θ del gas en función del tiempo τ en la parte superior y el desplazamiento del émbolo ξ en función del tiempo τ en la parte inferior

gamma=5.0/3;
delta=0.1;
mu=2.0; %gravedad adimensional
n=1; %número de moles
 
%x(1) es la temperatura, x(2) es la posición y x(3) es la velocidad
x0=[0.9,0.1,0];
fg=@(t,x) [-(gamma-1)*x(1)*x(3)/x(2)+delta*(gamma-1)*x(3)^2*sqrt(x(1))/x(2)-
(pi/8)*(gamma-1)*delta^2*x(3)^3/x(2); x(3); 
(n/x(2))*((pi/8)*delta^2*x(3)^2-delta*x(3)*sqrt(x(1))+x(1))-mu];
tspan=[0 50];
[t,x]=ode45(fg,tspan,x0);
subplot(2,1,1)
plot(t,x(:,1))
grid on
xlabel('t')
ylabel('\theta')
subplot(2,1,2)
plot(t,x(:,2))
grid on
xlabel('t')
ylabel('\xi')

Calculamos la energía inicial del sistema y comprobamos que se mantiene constante

>> mu*(gamma-1)*x0(2)+n*x0(1)
ans =    1.0333
>> 0.5*(gamma-1)*x(:,3).^2+mu*(gamma-1)*x(:,2)+n*x(:,1)
ans =
    1.0333
    1.0333
    1.0333
    1.0333
    .....

El estado final, como podemos comprobar midiendo la temperatura final y la posición final en la ventana gráfica con Data Cursor, es

>> xf=(mu*(gamma-1)*x0(2)+n*x0(1))/(mu*gamma)
xf =    0.3100
>> Tf=mu*xf/n
Tf =     0.6200

Actividades

Se introduce

• La posición inicial ξ₀ del émbolo en el control titulado Posición
• La temperatura inicial θ₀ del gas, en el control titulado Temperatura
• El valor de la gravedad adimensional μ, en el control titulado Gravedad
• El valor del parámetro δ, en el control titulado Parámetro

Se pulsa el botón titulado Nuevo

Observamos las oscilaciones del émbolo, hasta que al cabo de cierto tiempo alcanza la posición de equilibrio. El tiempo que tarda en alcanzar el estado de equilibrio depende de los valores de los parámetros δ y μ. Se sugiere al lector que ensaye el sistema para distintos valoes de dichos parámetros

El termómetro marca en cada instante τ la temperatura θ

Se representa la posición ξ del émbolo en función del tiempo τ.

En la parte superior derecha, se representa un diagrama en forma de tarta:

• en color azul, la energía interna del gas
• en color rojo, la energía potencial del émbolo
• en color gris, la energía cinética del émbolo

La energía total del sistema gas-embolo, la suma de las tres clases de energía, se mantiene constante. En caso contrario, querrá decir que el procedimiento numérico empleado en esta simulación no funciona adecuadamente.

Referencias

Bauman R. O., Cockerham III H. L. Pressure of an ideal gas on a moving piston. Am. J. Phys. 37 (7) July 1969, pp. 675-679

Carl E Mungan. Damped oscillations of a frictionless piston in an adiabatic cylinder enclosing an ideal gas. Eur. J. Phys. 38 (2017) 035102

Este artículo está disponible en la dirección: https://www.usna.edu/Users/physics/mungan/Publications/Publications.php#fndtn-panel120162017