Para un recinto cilíndrico infinitamente largo, el potencial no depende de z. La ecuación de Laplace se reduce a

${\displaystyle \frac{1}{\rho }\frac{\partial }{\partial \rho }\left(\rho \frac{\partial V}{\partial \rho }\right)+\frac{1}{{\rho }^2}\frac{{\partial }^{2}V}{\partial {\phi }^2}=0}$

La solución se escribe como producto de dos funciones una R(ρ) que depende solamente de ρ y otra F(φ), que depende solamente de φ. V(ρ,φ)=R(ρ)·F(φ)

${\displaystyle \begin{array}{l}F(\phi )\frac{1}{r}\frac{d}{dr}\left(r\frac{dR(r)}{dr}\right)+R(r)\frac{1}{r^2}\frac{d^{2}F(\phi )}{d{\phi }^2}=0\hfill \\ \frac{r}{R(r)}\frac{d}{dr}\left(r\frac{dR(r)}{dr}\right)=-\frac{1}{F(\phi )}\frac{d^{2}F(\phi )}{d{\phi }^2}=k^2\hfill \end{array}}$

Esto da lugar a dos ecuaciones diferenciales, como las analizadas en las páginas anteriores.

${\displaystyle \begin{array}{l}{\rho }^2\frac{d^{2}R}{d{\rho }^2}+\rho \frac{dR}{d\rho }-k^{2}R=0\\ \frac{d^{2}F}{d{\phi }^2}+k^{2}F=0\end{array}}$

Solución F(φ)

La solución de la segunda ecuación diferencial es sencilla,.

${\displaystyle F(\phi )=\{\begin{array}{l}A\cos (k\phi )+B\sin (k\phi ),k\ne 0\\ a_0\phi +b_0,k=0\end{array}}$

Solución R(ρ)

• Para k>0, hacemos la sustitución ρ=e^x, x=lnρ, quedando una ecuación diferencial de coeficientes constantes, cuya solución es inmediata

${\displaystyle \begin{array}{l}\frac{dR}{d\rho }=\frac{dR}{dx}\frac{dx}{d\rho }=\frac{dR}{dx}\frac{1}{\rho }=\frac{dR}{dx}{e}^{-x}\\ \frac{d^{2}R}{d{\rho }^2}=\frac{d}{d\rho }\left(\frac{dR}{d\rho }\right)=\frac{d}{dx}\left(\frac{dR}{d\rho }\right)\frac{dx}{d\rho }=\frac{d}{dx}\left(\frac{dR}{dx}{e}^{-x}\right)\frac{dx}{d\rho }=e^{-2x}\frac{d^{2}R}{d{x}^2}-e^{-2x}\frac{dR}{dx}\\ {\rho }^2\frac{d^{2}R}{d{\rho }^2}+\rho \frac{dR}{d\rho }-k^{2}R=0\\ e^{2x}\left(e^{-2x}\frac{d^{2}R}{d{x}^2}-e^{-2x}\frac{dR}{dx}\right)+e^x\left(\frac{dR}{dx}{e}^{-x}\right)-k^{2}R=0\\ \frac{d^{2}R}{d{x}^2}-k^{2}R=0\\ R=C{e}^{-kx}+D{e}^{kx}=C{\rho }^{-k}+D{\rho }^k\end{array}}$

• Para k=0, la solución de la primera ecuación diferencial es

${\displaystyle \begin{array}{l}\frac{d}{d\rho }\left(\rho \frac{dR}{d\rho }\right)=0\\ \frac{dR}{d\rho }=\frac{C}{\rho }\\ R(\rho )=C\ln \rho +D\end{array}}$

La solución, V(r,φ)=R(r)·F(φ), es el producto de

${\displaystyle F(\phi )=\{\begin{array}{l}A\cos (k\phi )+B\sin (k\phi )\\ a_0\phi +b_0\end{array}R(\rho )=\{\begin{array}{l}C{\rho }^{-k}+D{\rho }^k,k>0\\ c_0\ln \rho +d_0,k=0\end{array}}$

Recinto en forma de cuña (I)

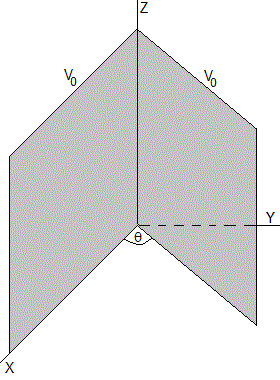
Supongamos dos conductores planos indefinidos al mismo potencial V₀ que forman una cuña de ángulo θ, tal como se muestra en la figura.

Las condiciones de contorno son

${\displaystyle \{\begin{array}{l}V(\rho \mathrm{,0})=V_0\\ V(\rho ,\theta )=V_0\end{array}}$

Cuando ρ→0 la solución V(r,φ)=R(r)·F(φ) debe ser finita por lo que se excluyen los términos lnρ y ρ^-k, por lo que c₀=0 y C=0

Para k=0, V₀=F(0)d₀ y V₀=F(θ)d₀

${\displaystyle \{\begin{array}{l}{V}_0=a_0·d_0\\ V_0=\left(a_0+b_0\theta \right)d_0\end{array}}$

lo que lleva a b₀=0.

Para k>0, con ρ≥0

${\displaystyle \{\begin{array}{l}\phi =\mathrm{0,}A=0\\ \phi =\theta ,A\cos (k\theta )+B\sin (k\theta )=0\end{array}}$

Lo que implica que sin(kθ)=0, kθ=nπ, n=1,2,3...

La solución de la ecuación de Laplace es la superposición

${\displaystyle V(\rho ,\phi )=V_0+{\displaystyle \sum _{n=1}^{\infty }\left(D_n{\rho }^{\frac{n\pi }{\theta }}\right)\left(B_n\sin \left(\frac{n\pi }{\theta }\phi \right)\right)}=V_0+{\displaystyle \sum _{n=1}^{\infty }{A}_n{\rho }^{\frac{n\pi }{\theta }}\sin \left(\frac{n\pi }{\theta }\phi \right)}}$

Precisamos de alguna condición más para determinar los coeficientes A_n. Véase el problema más abajo

Para pequeños valores de ρ, el potencial viene determinado esencialmente por el primer término

${\displaystyle V(\rho ,\phi )\approx V_0+A_1{\rho }^{\frac{\pi }{\theta }}\sin \left(\frac{\pi }{\theta }\phi \right)}$

Las componentes del campo eléctrico

${\displaystyle \begin{array}{l}{E}_{\rho }=-\frac{\partial V(\rho ,\phi )}{\partial \rho }=-\frac{\pi A_1}{\theta }{\rho }^{\pi /\theta -1}\sin \left(\frac{\pi \phi }{\theta }\right)\\ E_{\phi }=-\frac{1}{\vartheta }\frac{\partial V(\rho ,\phi )}{\partial \phi }=-\frac{\pi A_1}{\theta }{\rho }^{\pi /\theta -1}\cos \left(\frac{\pi \phi }{\theta }\right)\end{array}}$

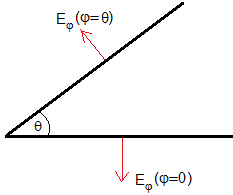
Las densidades de carga son iguales en ambos planos

${\displaystyle \begin{array}{l}\sigma (\rho \mathrm{,0})={\epsilon }_0{E}_{\phi }(\rho \mathrm{,0})=-{\epsilon }_0\frac{\pi A_1}{\theta }{\rho }^{\pi /\theta -1}\\ \sigma (\rho ,\theta )=-{\epsilon }_0{E}_{\phi }(\rho ,\theta )=-{\epsilon }_0\frac{\pi A_1}{\theta }{\rho }^{\pi /\theta -1}\end{array}}$

Cuando el ángulo de la cuña θ es pequeño la densidad de carga σ es grande

Recinto en forma de cuña (II)

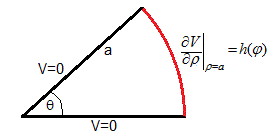
Sea un recinto en forma de cuña de ángulo θ y radio a que se extiende indefinidamente a lo largo del eje Z y cuya sección transversal, se muestra en la figura.

Sean las condiciones de contorno

${\displaystyle \{\begin{array}{l}V(\rho \mathrm{,0})=0\\ V(\rho ,\theta )=0\\ {\frac{\partial V(\rho ,\phi )}{\partial \rho }|}_{\rho =a}=h(\phi )\end{array}}$

Partimos de la solución de la ecuación de Laplace en coordenadas cilíndricas

${\displaystyle V(\rho ,\phi )=R(\rho )F(\phi )=\left(C{\rho }^{-k}+D{\rho }^k\right)\left(A\cos (k\phi )+B\sin (k\phi )\right)}$

Se descarta el término ρ^-k y lnρ, que se hacen infinito cuando ρ→0

La primera condición de contorno

${\displaystyle \begin{array}{l}V(\rho \mathrm{,0})=D{\rho }^k\left(A\cos (0)+B\sin (0)\right)=0\\ A=0\end{array}}$

La segunda condición de contorno

${\displaystyle \begin{array}{l}V(\rho ,\theta )=D{\rho }^{k}B\sin (k\theta )=0\\ k\theta =n\pi ,n=\mathrm{1,2,3...}\end{array}}$

El potencial V(ρ,φ) es la superposición

${\displaystyle V(\rho ,\phi )={\displaystyle \sum _{n=1}^{\infty }{D}_n{\rho }^{\frac{n\pi }{\theta }}\sin \left(\frac{n\pi }{\theta }\phi \right)}}$

La tercera condición de contorno

${\displaystyle {\frac{\partial V(\rho ,\phi )}{\partial \rho }|}_{\rho =a}={\displaystyle \sum _{n=1}^{\infty }{D}_n\frac{n\pi }{\theta }{a}^{\frac{n\pi }{\theta }-1}\sin \left(\frac{n\pi }{\theta }\phi \right)}=h(\phi )}$

nos permite calcular los coeficientes D_n de forma similar a un desarrollo en serie de Fourier, multiplicando por sin(mπφ/θ) e integrando entre 0 y θ

${\displaystyle \begin{array}{l}{\displaystyle \underset{0}{\overset{\theta }{\int }}h(\phi )\sin \left(\frac{m\pi }{\theta }\phi \right)d\phi }={\displaystyle \underset{0}{\overset{\theta }{\int }}\left({\displaystyle \sum _{n=1}^{\infty }{D}_n\frac{n\pi }{\theta }{a}^{\frac{n\pi }{\theta }-1}\sin \left(\frac{n\pi }{\theta }\phi \right)}\right)}\sin \left(\frac{m\pi }{\theta }\phi \right)d\phi \\ {\displaystyle \underset{0}{\overset{\theta }{\int }}h(\phi )\sin \left(\frac{m\pi }{\theta }\phi \right)d\phi }={\displaystyle \sum _{n=1}^{\infty }{D}_n\frac{n\pi }{\theta }{a}^{\frac{n\pi }{\theta }-1}{\displaystyle \underset{0}{\overset{\theta }{\int }}\sin \left(\frac{m\pi }{\theta }\phi \right)\sin \left(\frac{n\pi }{\theta }\phi \right)d\phi }}\\ {\displaystyle \underset{0}{\overset{\theta }{\int }}h(\phi )\sin \left(\frac{n\pi }{\theta }\phi \right)d\phi }=D_n\frac{n\pi }{\theta }{a}^{\frac{n\pi }{\theta }-1}\frac{\theta }{2}\end{array}}$

El potencial V(ρ,φ) es

${\displaystyle V(\rho ,\phi )=\frac{2a}{\pi }{\displaystyle \sum _{n=1}^{\infty }\frac{{\displaystyle \underset{0}{\overset{\theta }{\int }}h(\phi )\sin \left(\frac{n\pi }{\theta }\phi \right)d\phi }}{n}{\left(\frac{\rho }{a}\right)}^{\frac{n\pi }{\theta }}\sin \left(\frac{n\pi }{\theta }\phi \right)}}$

Ejemplo

Supongamos que h(φ)=h es constante

${\displaystyle V(\rho ,\phi )=\frac{4ha\theta }{{\pi }^2}{\displaystyle \sum _{n=\mathrm{1,3,5...}}^{\infty }\frac{1}{n^2}{\left(\frac{\rho }{a}\right)}^{\frac{n\pi }{\theta }}\sin \left(\frac{n\pi }{\theta }\phi \right)}}$

Si la cuña es recta, θ=π/2

${\displaystyle V(\rho ,\phi )=\frac{2ha}{\pi }{\displaystyle \sum _{n=\mathrm{1,3,5...}}^{\infty }\frac{1}{n^2}{\left(\frac{\rho }{a}\right)}^{2n}\sin \left(2n\phi \right)}}$

Definimos una función que calcula el potencial V(ρ,z), empleando N=100 términos del desarrollo en serie

function res = laplace_potencial_13(rho,phi, N)
    res=0;
    for n=1:N
         res=res+2*sin(2*(2*n-1)*phi).*rho.^(2*(2*n-1))/((2*n-1)^2*pi);
    end
end

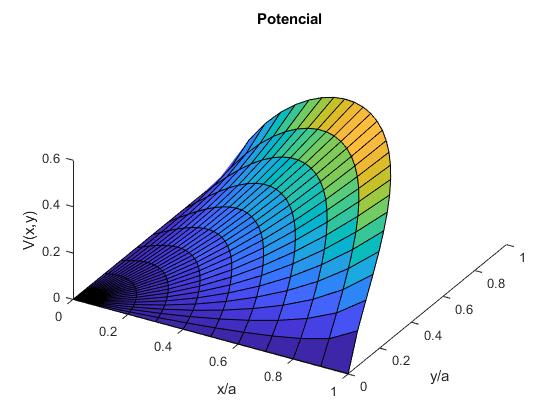
Representamos la función V(ρ,z), mediante surf

N=100;
r=0:0.1:1;
ang=0:pi/50:pi/2;
[r,ang]=meshgrid(r,ang);
x=r.*cos(ang);
y=r.*sin(ang);
z=laplace_potencial_13(r,ang,N);
hold on
surf(x,y,z)
xlabel('x/a')
ylabel('y/a')
zlabel('V(x,y)')
title('Potencial')
view(30,47)

Condensador cilíndrico

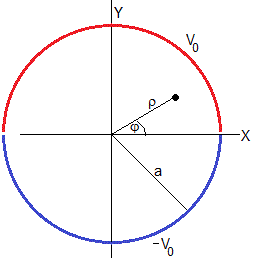
Consideramos una superficie cilíndrica muy larga de radio a, cuya sección transversal mostramos en la figura. Supongamos que la mitad superior se mantiene a un potencial V₀ y la mitad inferior a un potencial -V₀. Queremos calcular el potencial en un punto (ρ, φ) interior o exterior al conductor. Las condiciones de contorno son:

${\displaystyle V(a,\phi )=\{\begin{array}{l}{V}_{0}0<\phi <\pi \\ -V_0\pi <\phi <2\pi \end{array}}$

F(φ)=F(φ+2π) tiene que ser una función periódica

${\displaystyle \begin{array}{l}A\cos (k\phi )+B\sin (k\phi )=A\cos \left(k(\phi +2\pi )\right)+B\sin \left(k(\phi +2\pi )\right)\\ \sin \left(\alpha +k\phi \right)=\sin \left(\alpha +k(\phi +2\pi )\right),\tan \alpha =\frac{A}{B}\end{array}}$

Aplicando la fórmula de la diferencia de senos, sin(a+b)-sin(a-b)=2sinb·cosa

${\displaystyle \begin{array}{l}\{\begin{array}{l}a+b=\alpha +k(\phi +2\pi )\\ a-b=\alpha +k\phi \end{array}\{\begin{array}{l}a=\alpha +k(\phi +\pi )\\ b=k\pi \end{array}\\ \sin \left(k\pi \right)\cos \left(\alpha +k(\phi +\pi )\right)=\mathrm{0,}k=n,\text{entero}\end{array}}$

La solución de la ecuación de Laplace es la superposición

${\displaystyle V(\rho ,\phi )={\displaystyle \sum _{n=1}^{\infty }\left(C_n{\rho }^{-n}+D_n{\rho }^n\right)\left(A\cos (n\phi )+B\sin (n\phi )\right)}}$

En φ=0, V(a,0)=0 y en φ=π, V(a,π)=0 por lo que el coeficiente A=0

${\displaystyle V(\rho ,\phi )={\displaystyle \sum _{n=1}^{\infty }\left(C_n{\rho }^{-n}+D_n{\rho }^n\right)\sin (n\phi )}}$

Interior del recinto cilíndrico, ρ<a

Para ρ<a, se ha de excluir el término ρ^-n, que se hace infinito cuando ρ→0.

${\displaystyle V(\rho ,\phi )={\displaystyle \sum _{n=1}^{\infty }{D}_n{\rho }^n\sin (n\phi )}}$

La condición de contorno en ρ=a,

${\displaystyle V(a,\phi )={\displaystyle \sum _{n=1}^{\infty }{D}_n{a}^n\sin (n\phi )}}$

nos permite calcular los coeficientes D_n de forma similar a un desarrollo en serie de Fourier, multiplicando por sin(mφ) e integrando entre 0 y 2π

${\displaystyle \begin{array}{l}{\displaystyle \underset{0}{\overset{2\pi }{\int }}V(a,\phi )\sin (m\phi )d\phi }={\displaystyle \underset{0}{\overset{2\pi }{\int }}\left({\displaystyle \sum _{n=1}^{\infty }{D}_n{a}^n\sin (n\phi )}\right)}\sin (m\phi )d\phi \\ V_0{\displaystyle \underset{0}{\overset{\pi }{\int }}\sin (m\phi )d\phi }-V_0{\displaystyle \underset{\pi }{\overset{2\pi }{\int }}\sin (m\phi )d\phi }={\displaystyle \sum _{n=1}^{\infty }{D}_n{a}^n{\displaystyle \underset{0}{\overset{2\pi }{\int }}\sin (n\phi )\sin (m\phi )d\phi }}\\ D_n=\{\begin{array}{l}\frac{4V_0}{n{a}^n\pi }n\text{impar}\\ 0n\text{par}\end{array}\end{array}}$

El potencial

${\displaystyle V(\rho ,\phi )=\frac{4V_0}{\pi }{\displaystyle \sum _{n=\mathrm{1,3,5...}}^{\infty }\frac{{\rho }^n}{n{a}^n}\sin (n\phi )},\rho <a}$

Exterior del recinto cilíndrico, ρ>a

Para ρ>a, se ha de excluir el término ρⁿ, que se hace infinito cuando ρ→∞.

${\displaystyle V(\rho ,\phi )={\displaystyle \sum _{n=1}^{\infty }{C}_n{\rho }^{-n}\sin (n\phi )}}$

La condición de contorno en ρ=a

${\displaystyle V(a,\phi )={\displaystyle \sum _{n=1}^{\infty }\frac{C_n}{a^n}\sin (n\phi )}}$

nos permite calcular los coeficientes C_n de forma similar a un desarrollo en serie de Fourier, multiplicando por sin(mφ) e integrando entre 0 y 2π

${\displaystyle \begin{array}{l}{\displaystyle \underset{0}{\overset{2\pi }{\int }}V(a,\phi )\sin (m\phi )d\phi }={\displaystyle \underset{0}{\overset{2\pi }{\int }}\left({\displaystyle \sum _{n=1}^{\infty }\frac{C_n}{a^n}\sin (n\phi )}\right)}\sin (m\phi )d\phi \\ V_0{\displaystyle \underset{0}{\overset{\pi }{\int }}\sin (m\phi )d\phi }-V_0{\displaystyle \underset{\pi }{\overset{2\pi }{\int }}\sin (m\phi )d\phi }={\displaystyle \sum _{n=1}^{\infty }\frac{C_n}{a^n}{\displaystyle \underset{0}{\overset{2\pi }{\int }}\sin (n\phi )\sin (m\phi )d\phi }}\\ C_n=\{\begin{array}{l}\frac{4V_0{a}^n}{n\pi }n\text{impar}\\ 0n\text{par}\end{array}\end{array}}$

El potencial

${\displaystyle V(\rho ,\phi )=\frac{4V_0}{\pi }{\displaystyle \sum _{n=\mathrm{1,3,5...}}^{\infty }\frac{a^n}{n{\rho }^n}\sin (n\phi )},\rho >a}$

Ejemplo

Sea un cilindro muy largo de radio a=1

Definimos una función que calcula el potencial V(ρ,z), para ρ<a, empleando N=100 términos del desarrollo en serie

function res = laplace_potencial_11(rho,phi, N)
    res=0;
    for n=1:N
         res=res+4*sin((2*n-1)*phi).*rho.^n/((2*n-1)*pi);
    end
end

Definimos otra función que calcula el potencial V(ρ,φ), para ρ>a, empleando N=100 términos del desarrollo en serie

function res = laplace_potencial_12(rho,phi, N)
    res=0;
    for n=1:N
         res=res+4*sin((2*n-1)*phi)./((2*n-1)*pi*rho.^n);
    end
end

Representamos la función V(ρ,z) para ρ<a y para ρ>a, mediante surf

N=100;
%interior del cilindro, r<a
r=0:0.1:1;
ang=0:pi/50:2*pi;
[r,ang]=meshgrid(r,ang);
x=r.*cos(ang);
y=r.*sin(ang);
z=laplace_potencial_11(r,ang,N);
hold on
surf(x,y,z) %potencial en el interior

%exterior r>a
r=1:0.1:1.5;
ang=0:pi/50:2*pi;
[r,ang]=meshgrid(r,ang);
x=r.*cos(ang);
y=r.*sin(ang);
z=laplace_potencial_12(r,ang,N);
surf(x,y,z) %potencial en el exterior

hold off
xlabel('x')
ylabel('y')
zlabel('V(x,y)')
title('Potencial')
view(73,40)

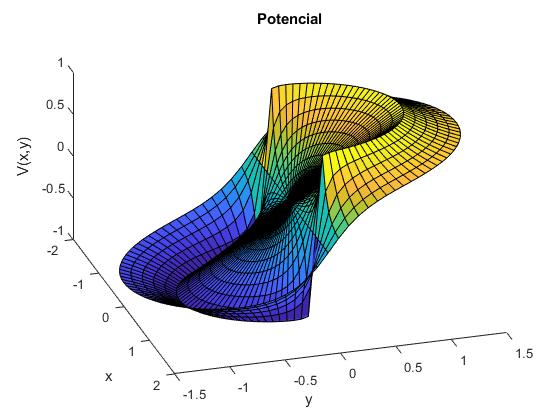
Para mayor claridad, se recomienda visualizar primero el potencial en el interior, primera sentencia surf y después el exterior, segunda sentencia surf, poniendo delante el carácter comentarios %

Dos cilindros concéntricos

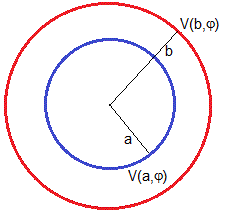
Sean dos cilindros concéntrico muy largos, de radios a y b, cuyo eje común es Z. En la figura se muestra la sección transversal. Estudiaremos el potencial en el espacio comprendido entre los dos cilindros

Las condiciones de contorno son:

• para ρ=a, el potencial es V(a, φ)
• para ρ=b, el potencial es V(b, φ)

Como en el ejemplo anterior F(φ) es una función periódica, k=n es un entero. Por otra parte, no se alcanza el el centro ρ≠0, por lo que no se pueden excluir los términos proporcionales a lnρ y ρ^-k. La solución completa es la superposición

${\displaystyle V(\rho ,\phi )=c_0+d_0\ln \rho +{\displaystyle \sum _{n=1}^{\infty }\left(C_n{\rho }^{-n}+D_n{\rho }^n\right)\left(A_n\cos (n\phi )+B_n\sin (n\phi )\right)}}$

Expresamos de otra forma, renombrando los coeficientes

${\displaystyle V(\rho ,\phi )=A_0+B_0\ln \rho +{\displaystyle \sum _{n=1}^{\infty }\left\{\left(A_n{\rho }^{-n}+B_n{\rho }^n\right)\cos (n\phi )+\left(C_n{\rho }^{-n}+D_n{\rho }^n\right)\sin (n\phi )\right\}}}$

que nos permita calcular los coeficientes de forma similar a un desarrollo en serie de Fourier.

• Integramos entre 0 y 2π

${\displaystyle {\displaystyle \underset{0}{\overset{2\pi }{\int }}V(a,\phi )·d\phi }=\left(A_0+B_0\ln a\right){\displaystyle \underset{0}{\overset{2\pi }{\int }}d\phi }+{\displaystyle \sum _{n=1}^{\infty }\left\{\left(A_n{a}^{-n}+B_n{a}^n\right){\displaystyle \underset{0}{\overset{2\pi }{\int }}\cos (n\phi )·d\phi }+\left(C_n{a}^{-n}+D_n{a}^n\right){\displaystyle \underset{0}{\overset{2\pi }{\int }}\sin (n\phi )·d\phi }\right\}}}$

El resultado es

${\displaystyle \{\begin{array}{l}{\displaystyle \underset{0}{\overset{2\pi }{\int }}V(a,\phi )·d\phi }=\left(A_0+B_0\ln a\right)2\pi \\ {\displaystyle \underset{0}{\overset{2\pi }{\int }}V(b,\phi )·d\phi }=\left(A_0+B_0\ln b\right)2\pi \end{array}}$

Un sistema de dos ecuaciones con dos incógnitas, despejamos A₀ y B₀

• Multiplicamos por sin(nφ) e integramos entre 0 y 2π

${\displaystyle {\displaystyle \underset{0}{\overset{2\pi }{\int }}V(a,\phi )·\sin (n\phi )·d\phi }=\left(A_0+B_0\ln a\right){\displaystyle \underset{0}{\overset{2\pi }{\int }}\sin (n\phi )·d\phi }+{\displaystyle \sum _{n=1}^{\infty }\left\{\left(A_n{a}^{-n}+B_n{a}^n\right){\displaystyle \underset{0}{\overset{2\pi }{\int }}\cos (n\phi )·\sin (n\phi )·d\phi }+\left(C_n{a}^{-n}+D_n{a}^n\right){\displaystyle \underset{0}{\overset{2\pi }{\int }}{\sin }^2(n\phi )·d\phi }\right\}}}$

El resultado es

${\displaystyle \{\begin{array}{l}{\displaystyle \underset{0}{\overset{2\pi }{\int }}V(a,\phi )·\sin (n\phi )·d\phi }=\left(C_n\frac{1}{a^n}+D_n{a}^n\right)\pi \\ {\displaystyle \underset{0}{\overset{2\pi }{\int }}V(b,\phi )·\sin (n\phi )·d\phi }=\left(C_n\frac{1}{b^n}+D_n{b}^n\right)\pi \end{array}}$

Un sistema de dos ecuaciones con dos incógnitas, despejamos C_n y D_n, n=1,2,3...

• Multiplicamos por cos(nφ) e integramos entre 0 y 2π

${\displaystyle {\displaystyle \underset{0}{\overset{2\pi }{\int }}V(a,\phi )·\cos (n\phi )·d\phi }=\left(A_0+B_0\ln a\right){\displaystyle \underset{0}{\overset{2\pi }{\int }}\cos (n\phi )·d\phi }+{\displaystyle \sum _{n=1}^{\infty }\left\{\left(A_n{a}^{-n}+B_n{a}^n\right){\displaystyle \underset{0}{\overset{2\pi }{\int }}{\cos }^2(n\phi )·d\phi }+\left(C_n{a}^{-n}+D_n{a}^n\right){\displaystyle \underset{0}{\overset{2\pi }{\int }}\sin (n\phi )·\cos (n\phi )·d\phi }\right\}}}$

El resultado es

${\displaystyle \{\begin{array}{l}{\displaystyle \underset{0}{\overset{2\pi }{\int }}V(a,\phi )·\cos (n\phi )·d\phi }=\left(A_n\frac{1}{a^n}+B_n{a}^n\right)\pi \\ {\displaystyle \underset{0}{\overset{2\pi }{\int }}V(b,\phi )·\cos (n\phi )·d\phi }=\left(A_n\frac{1}{b^n}+B_n{b}^n\right)\pi \end{array}}$

Un sistema de dos ecuaciones con dos incógnitas, despejamos A_n y B_n, n=1,2,3...

Ejemplo 1

Sea

• a=1, V(1, φ)=2

• b=2, V(2, φ)=1

${\displaystyle \begin{array}{l}\{\begin{array}{l}{\displaystyle \underset{0}{\overset{2\pi }{\int }}V(a,\phi )·d\phi }=\left(A_0+B_0\ln a\right)2\pi \\ {\displaystyle \underset{0}{\overset{2\pi }{\int }}V(b,\phi )·d\phi }=\left(A_0+B_0\ln b\right)2\pi \end{array}\\ \{\begin{array}{l}2·2\pi =\left(A_0+B_0\ln 1\right)2\pi \\ 1·2\pi =\left(A_0+B_0\ln 2\right)2\pi \end{array}\end{array}}$

A₀=2, B₀=-1/ln2, los demás coeficientes son nulos

${\displaystyle V(\rho ,\phi )=2-\frac{\ln \rho }{\ln 2}}$

Un ejemplo similar, es el condensador cilíndrico, el campo eléctrico se calcula aplicando la ley de Gauss

Ejemplo 2

Sea

• a=1, V(1, φ)=0

• b=2, V(2, φ)=cosφ

${\displaystyle \begin{array}{l}\{\begin{array}{l}{\displaystyle \underset{0}{\overset{2\pi }{\int }}V(a,\phi )·\cos (\phi )·d\phi }=\left(\frac{1}{a}{A}_1+a{B}_1\right)\pi \\ {\displaystyle \underset{0}{\overset{2\pi }{\int }}V(b,\phi )·\cos (\phi )·d\phi }=\left(\frac{1}{b}{A}_1+b{B}_1\right)\pi \end{array}\\ \{\begin{array}{l}0=\left(\frac{1}{1}{A}_1+1B_1\right)\pi \\ \pi =\left(\frac{1}{2}{A}_1+2B_1\right)\pi \end{array}\end{array}}$

A₁=-2/3, B₁=2/3, los demás coeficientes son nulos

${\displaystyle V(\rho ,\phi )=\left(A_1{\rho }^{-1}+B_1{\rho }^1\right)\cos \phi =\frac{2}{3}\left(\rho -\frac{1}{\rho }\right)\cos \phi }$

Referencias

Matthew N. O. Sadiku, Numerical Techniques in Electromagnetics. Second Edition 2001, CRC Press. Sección 2.4

https://www.math.uh.edu/~pwalker/laplace6.pdf

John David Jackson. Classical Electrodynamics. John Wiley & Sons, Inc. (1999), pp. 75-77