El potencial truncado es

${\displaystyle V(x)=\{\begin{array}{l}-V_0\frac{a_0\delta }{\left|x\right|},\left|x\right|\ge a_0\delta \\ -V_0,\left|x\right|<a_0\delta \end{array}}$

cuya representación gráfica es

f=@(x) -1./abs(x); 
hold on
fplot(f,[0.5,10],'r')
fplot(f,[-10,-0.5],'r')
line([-0.5,0.5],[-2,-2],'color','r')
hold off
axis off

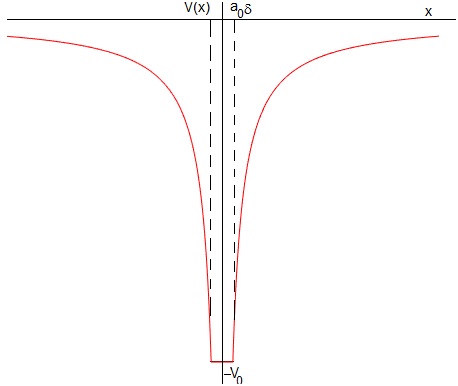
Donde $a_0=\frac{4\pi {\epsilon }_0{\hslash }^2}{m{e}^2}$, es el radio de Bohr, m es la masa del electrón, e es su carga, δ es un parámetro positivo y $V_0=\frac{e^2}{4\pi {\epsilon }_0{a}_0\delta }$

En la región I, |x|<a₀δ, la ecuación de Schrödinger es

${\displaystyle \begin{array}{l}\frac{-{\hslash }^2}{2m}\frac{d^2\psi }{d{x}^2}-V_0\psi (x)=E\psi (x)\\ \frac{d^2\psi }{d{x}^2}+q^2\psi (x)=\mathrm{0,}{q}^2=\frac{2m}{{\hslash }^2}\left(E+V_0\right)\end{array}}$

La solución de esta ecuación diferencial es conocida

${\displaystyle {\psi }_I(x)=A_1\cos (qx)+B_1\sin (qx)}$

• Las solución simétrica ψ(-x)=ψ(x), se obtiene cuando B₁=0

• Las solución antisimétrica ψ(-x)=-ψ(x), se obtiene cuando A₁=0

En la región II, |x|≥a₀δ, la ecuación de Schrödinger es

${\displaystyle \frac{-{\hslash }^2}{2m}\frac{d^2\psi }{d{x}^2}-\frac{e^2}{4\pi {\epsilon }_0\left|x\right|}\psi (x)=E\psi (x)}$

Definimos el parámetro β tal que

${\displaystyle \begin{array}{l}E=-\frac{{\hslash }^2}{2m{a}_0^2\beta },y=\frac{x}{a_0\beta }\\ q=\frac{1}{a_0}\sqrt{\frac{2}{\delta }-\frac{1}{{\beta }^2}}\end{array}}$

La ecuación de Schrödinger se convierte en

${\displaystyle \frac{d^2\psi }{d{y}^2}+\frac{2\beta }{\left|y\right|}\psi (y)-\psi (y)=0}$

Hacemos el cambio de variable

${\displaystyle \begin{array}{l}\psi (y)=y{e}^{-y}f(y)\\ \frac{d\psi (y)}{dy}=e^{-y}\left(1-y\right)f(y)+y{e}^{-y}\frac{df(y)}{dy}\\ \frac{d^2\psi (y)}{d{y}^2}=e^{-y}\left(-2+y\right)f(y)+2e^{-y}\left(1-y\right)\frac{df(y)}{dy}+y{e}^{-y}\frac{d^{2}f(y)}{d{y}^2}\end{array}}$

Obtenemos la ecuación diferencial, válida para y≥0

${\displaystyle \begin{array}{l}y\frac{d^{2}f}{d{y}^2}+2\left(1-y\right)\frac{df}{dy}+2\left(\beta \frac{y}{\left|y\right|}-1\right)f=0\\ y\frac{d^{2}f}{d{y}^2}+2\left(1-y\right)\frac{df}{dy}-2\left(1-\beta \right)f=\mathrm{0,}y\ge 0\end{array}}$

Llamando z=2y

${\displaystyle z\frac{d^{2}f}{d{z}^2}+\left(2-z\right)\frac{df}{dz}-\left(1-\beta \right)f=0}$

Esta ecuación diferencial es de un tipo, cuya solución es conocida

${\displaystyle \begin{array}{l}z\frac{d^{2}w}{d{z}^2}+\left(b-z\right)\frac{dw}{dz}-aw=0\\ w(z)=A_{2}M(a,b;z)+B_{2}U(a,b;z),\{\begin{array}{l}a=1-\beta \\ b=2\end{array}\end{array}}$

Deshacemos los cambios de variable

${\displaystyle \begin{array}{l}f(y)=A_{2}M\left(1-\beta \mathrm{,2};2y\right)+B_{2}U\left(1-\beta \mathrm{,2};2y\right)\\ \psi (y)=y{e}^{-y}\left(A_{2}M\left(1-\beta \mathrm{,2};2y\right)+B_{2}U\left(1-\beta \mathrm{,2};2y\right)\right)\\ {\psi }_{II}(x)=\frac{x}{a_0\beta }\exp \left(-\frac{x}{a_0\beta }\right)\left(A_{2}M\left(1-\beta \mathrm{,2};\frac{2x}{a_0\beta }\right)+B_{2}U\left(1-\beta \mathrm{,2};\frac{2x}{a_0\beta }\right)\right)\end{array}}$

Para que ψ(x) sea finito (tienda a cero) cuando x→∞, entonces A₂=0

${\displaystyle {\psi }_{II}(x)=B_2\frac{x}{a_0\beta }\exp \left(-\frac{x}{a_0\beta }\right)U\left(1-\beta \mathrm{,2};\frac{2x}{a_0\beta }\right)}$

U(a,b,z), es la función hipergeométrica confluente de Kummer

La solución simétrica, ψ(-x)=ψ(x)

La función de onda en las regiones I y II es

${\displaystyle \psi (x)=\{\begin{array}{l}{A}_1\cos \left(qx\right),x<a_0\delta \\ B_2\frac{x}{a_0\beta }\exp \left(-\frac{x}{a_0\beta }\right)U\left(1-\beta \mathrm{,2};\frac{2x}{a_0\beta }\right),x\ge a_0\delta \end{array}}$

Teniendo en cuenta que

${\displaystyle \begin{array}{l}\frac{d}{dz}U(a,b;z)=-aU(a+\mathrm{1,}b+1;z),z=2y\\ \frac{d}{dy}U(1-\beta \mathrm{,2};2y)=2\left(1-\beta \right)U(2-\beta \mathrm{,3};2y),y=\frac{x}{a_0\beta }\\ \frac{d}{dx}U\left(1-\beta \mathrm{,2};\frac{2x}{a_0\beta }\right)=\frac{2\left(1-\beta \right)}{a_0\beta }U\left(2-\beta \mathrm{,3};\frac{2x}{a_0\beta }\right)\end{array}}$

La condición de continuidad de la función de onda y de la derivada primera en x=a₀δ se expresa

${\displaystyle \{\begin{array}{l}{A}_1\cos \left(q{a}_0\delta \right)=B_2\frac{\delta }{\beta }\exp \left(-\frac{\delta }{\beta }\right)U\left(1-\beta \mathrm{,2};\frac{2\delta }{\beta }\right)\\ -A_{1}q\sin \left(q{a}_0\delta \right)=\frac{B_2}{a_0\beta }\exp \left(-\frac{\delta }{\beta }\right)\left\{\left(1-\frac{\delta }{\beta }\right)U\left(1-\beta \mathrm{,2};\frac{2\delta }{\beta }\right)-2\left(1-\beta \right)\frac{a_0\delta }{a_0\beta }U\left(2-\beta \mathrm{,3};\frac{2\delta }{\beta }\right)\right\}\end{array}}$

Dividiendo la segunda entre la primera, obtenemos una ecuación trascendente, cuyas raíces nos dan los valores de β, o los niveles de energía E_n

${\displaystyle -q{a}_0\delta \tan \left(q{a}_0\delta \right)=1-\frac{\delta }{\beta }-2\left(1-\beta \right)\frac{\delta }{\beta }\frac{U\left(2-\beta \mathrm{,3};\frac{2\delta }{\beta }\right)}{U\left(1-\beta \mathrm{,2};\frac{2\delta }{\beta }\right)},q{a}_0=\sqrt{\frac{2}{\delta }-\frac{1}{{\beta }^2}}}$

Calculamos los valores de β para δ=10^-3

function hipergeometrica_6   
    delta=1e-3;
    f=@(x) delta*sqrt(2/delta-1./x.^2).*tan(sqrt(2/delta-1./x.^2)*delta)+
(1-delta./x)-2*delta*(1-x).*kummerU(2-x,3,2*delta./x)./
(x.*kummerU(1-x,2,2*delta./x));
    x=linspace(0,4,50);
    rPar=raices(f,x);
    disp(rPar)
    hold on
    fplot(f,[0,3.5])
    for j=1:length(rPar)
          plot(rPar(j),0, 'ro','markersize',3,'markerfacecolor','r')
    end
    hold off
    grid on
    ylim([-3,3])
    xlabel('x/a_0')
    ylabel('f(x)')
    title('Raíces de la ecuación transcendente')

     function r = raices(f, x)
        y=f(x);
        indices=find(y(1:end-1).*y(2:end)<0);
        r=zeros(1,length(indices));
        for k=1:length(indices)
            r(k)=fzero(f, [x(indices(k)), x(indices(k)+1)]);
        end
     end
end

0.1085    1.0020    1.1510    2.0020    2.1519    3.0020    3.1521

Representamos las raíces mediante puntos de color rojo

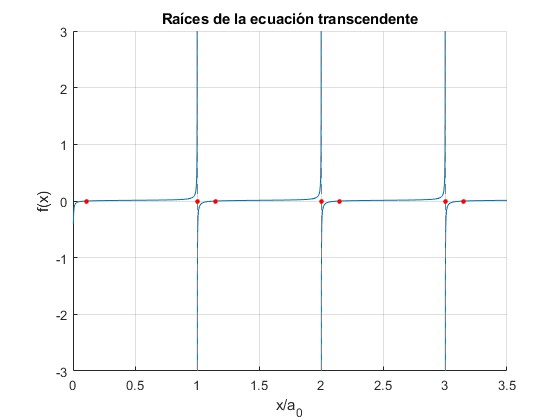
Las raíces 1.0020, 2.0020 y 3.0020 no corresponden a esta simetría. Como ya hemos visto en otros ejemplos, la forma de la función f(x)=0, no es la adecuada para calcular las raíces de una ecuación transcendente. La transformamos en

${\displaystyle \left\{\left(\beta -\delta \right)U\left(1-\beta \mathrm{,2};\frac{2\delta }{\beta }\right)-2\delta \left(1-\beta \right)U\left(2-\beta \mathrm{,3};\frac{2\delta }{\beta }\right)\right\}\cos \left(q{a}_0\delta \right)+\beta q{a}_0\delta \sin \left(q{a}_0\delta \right)U\left(1-\beta \mathrm{,2};\frac{2\delta }{\beta }\right)=0}$

function hipergeometrica_7   
    delta=1e-3;
    x=linspace(0,4,50);
    rPar=raices(@par,x);
    disp(rPar)
    hold on
    fplot(@par,[0,3.5])
    for j=1:length(rPar)
          plot(rPar(j),0, 'ro','markersize',3,'markerfacecolor','r')
    end
    hold off
    grid on
    ylim([-10,10])
    xlabel('x/a_0')
    ylabel('f(x)')
    title('Raíces de la ecuación transcendente')

    function res=par(x)
         q=sqrt(2/delta-1./x.^2);
         u_2=kummerU(1-x,2,2*delta./x);
         u_3=kummerU(2-x,3,2*delta./x);
        res=((x-delta).*u_2-2*delta*(1-x).*u_3).*cos(q*delta)+delta*(x.*u_2).
*(q.*sin(q*delta));
     end


     function r = raices(f, x)
        y=f(x);
        indices=find(y(1:end-1).*y(2:end)<0);
        r=zeros(1,length(indices));
        for k=1:length(indices)
            r(k)=fzero(f, [x(indices(k)), x(indices(k)+1)]);
        end
     end
end

 0.1085    1.1510    2.1519    3.1521

Representamos las raíces mediante puntos de color rojo

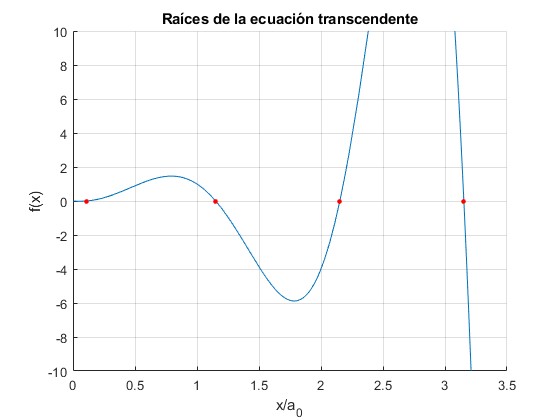
Cuando δ disminuye por ejemplo, δ=10^-5, la función f(x) es casi tangente al eje X cerca del origen, por este motivo, ya no se obtiene la primera raíz, x/a₀≈0

Funciones de onda

${\displaystyle \begin{array}{l}\psi (x)=\{\begin{array}{l}{A}_1\cos \left(qx\right),x<a_0\delta \\ B_2\frac{x}{a_0\beta }\exp \left(-\frac{x}{a_0\beta }\right)U\left(1-\beta \mathrm{,2};\frac{2x}{a_0\beta }\right),x\ge a_0\delta \end{array}\\ A_1\cos \left(q{a}_0\delta \right)=B_2\frac{\delta }{\beta }\exp \left(-\frac{\delta }{\beta }\right)U\left(1-\beta \mathrm{,2};\frac{2\delta }{\beta }\right)\end{array}}$

La última expresión relaciona los coeficientes A₁ y B₂

Por razones de simetría, se deberá cumplir que

${\displaystyle {\displaystyle \underset{0}{\overset{\infty }{\int }}{\left|\psi (x)\right|}^{2}dx=\frac{1}{2}}}$

Lo que nos permite determinar A₁

${\displaystyle A_1^2{\displaystyle \underset{0}{\overset{a_0\delta }{\int }}{\cos }^2\left(qx\right)dx+\frac{B_2^2}{{\left(a_0\beta \right)}^2}}{\displaystyle \underset{a_0\delta }{\overset{\infty }{\int }}{x}^2\exp \left(-\frac{2x}{a_0\beta }\right)U^2\left(1-\beta \mathrm{,2};\frac{2x}{a_0\beta }\right)}dx=\frac{1}{2}}$

Haciendo el cambio de variable, z=x/(a₀δ)

${\displaystyle \begin{array}{l}{A}_1^2{a}_0\delta \left\{{\displaystyle \underset{0}{\overset{1}{\int }}{\cos }^2\left(q{a}_0\delta z\right)dz+\frac{{\cos }^2\left(q{a}_0\delta \right)}{\exp \left(-\frac{2\delta }{\beta }\right)U^2\left(1-\beta \mathrm{,2};\frac{2\delta }{\beta }\right)}}{\displaystyle \underset{1}{\overset{\infty }{\int }}{z}^2\exp \left(-\frac{2\delta }{\beta }z\right)U^2\left(1-\beta \mathrm{,2};\frac{2\delta }{\beta }z\right)}dz\right\}=\frac{1}{2}\\ A_1^2{a}_0\delta \left\{\frac{1}{2}\left(1+\frac{\sin \left(2q{a}_0\delta \right)}{2q{a}_0\delta }\right)+\frac{{\cos }^2\left(q{a}_0\delta \right)}{\exp \left(-\frac{2\delta }{\beta }\right)U^2\left(1-\beta \mathrm{,2};\frac{2\delta }{\beta }\right)}{\displaystyle \underset{1}{\overset{\infty }{\int }}{z}^2\exp \left(-\frac{2\delta }{\beta }z\right)U^2\left(1-\beta \mathrm{,2};\frac{2\delta }{\beta }z\right)}dz\right\}=\frac{1}{2}\end{array}}$

Despejamos A₁ y calculamos B₂

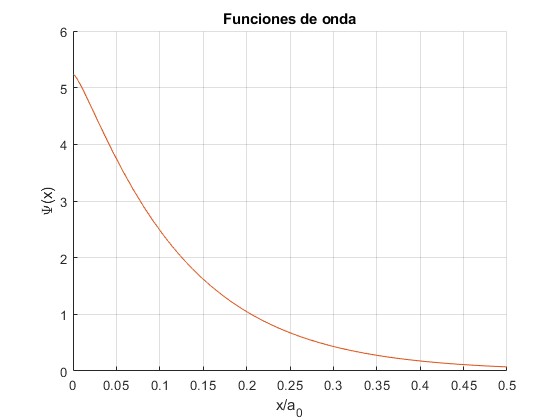
Representamos la función de onda del estado fundamental, β=0.1085, para δ=10^-3. Comprobamos que la función de onda es continua para x/a₀=10^-3

beta=0.1085;
 delta=1e-3;
 f=@(x) x.*exp(-x*delta/beta).*kummerU(1-beta,2,2*delta*x/beta);
 g=@(x) f(x).^2;
 area1=integral(g,1,20);
 q=sqrt(2/delta-1/beta^2);
 area=(1+sin(2*q*delta)/(2*q*delta))/2+cos(q*delta)^2*area1/(exp(-2*delta/beta)*
kummerU(1-beta,2,2*delta/beta)^2);
 A1=sqrt(0.5/(delta*area));
 B2=A1*cos(q*delta)*beta/(delta*exp(-delta/beta)*kummerU(1-beta,2,2*delta/beta));
 hold on
 f1=@(x) A1*cos(q*x);
 fplot(f1 ,[0,delta])
 f2=@(x) B2*(x.*exp(-x/beta)).*kummerU(1-beta,2,2*x/beta)/beta;
 fplot(f2 ,[delta, 0.5])
 hold off
 grid on
 xlabel('x/a_0')
 xlim([0,5*delta])
 ylabel('\Psi(x)')
 title('Funciones de onda')

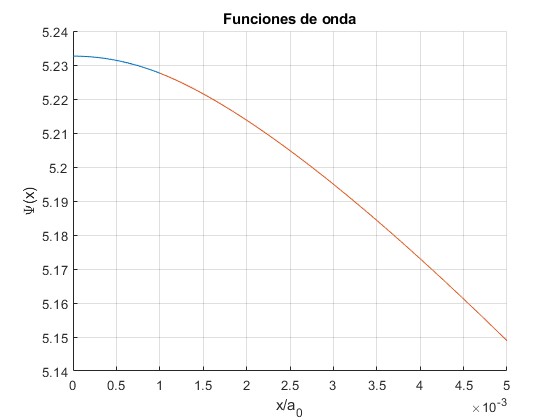
Representamos la función de onda hasta x/a₀=0.5, anulando la sentencia xlim([0,5*delta])

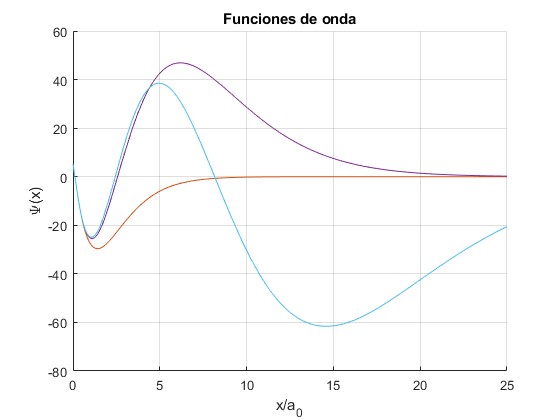
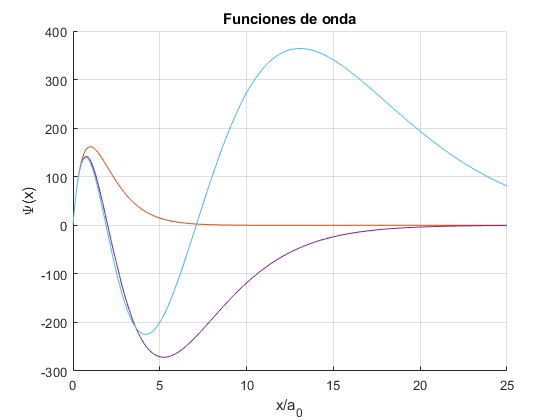
Representamos las funciones de onda para los niveles, β=1.1510, 2.1519, 3.1521, calculados para δ=10^-3.

 delta=1e-3;
 for beta=[1.1510,2.1519,3.1521]
     f=@(x) x.*exp(-x*delta/beta).*kummerU(1-beta,2,2*delta*x/beta);
     g=@(x) f(x).^2;
     area1=integral(g,1,20);
     q=sqrt(2/delta-1/beta^2);
     area=(1+sin(2*q*delta)/(2*q*delta))/2+cos(q*delta)^2*area1/(exp(-2*delta/beta)
*kummerU(1-beta,2,2*delta/beta)^2);
     A1=sqrt(0.5/(delta*area));
     B2=A1*cos(q*delta)*beta/(delta*exp(-delta/beta)*kummerU(1-beta,2,2*delta/beta));
     hold on
     f1=@(x) A1*cos(q*x);
     fplot(f1 ,[0,delta])
     f2=@(x) B2*(x.*exp(-x/beta)).*kummerU(1-beta,2,2*x/beta)/beta;
     fplot(f2, [delta, 25])
 end
 hold off
 grid on
 xlabel('x/a_0')
 ylabel('\Psi(x)')
 title('Funciones de onda')

La solución antisimétrica, ψ(-x)=-ψ(x)

La función de onda en las regiones I y II es

${\displaystyle \psi (x)=\{\begin{array}{l}{B}_1\sin \left(qx\right),x<a_0\delta \\ B_2\frac{x}{a_0\beta }\exp \left(-\frac{x}{a_0\beta }\right)U\left(1-\beta \mathrm{,2};\frac{2x}{a_0\beta }\right),x\ge a_0\delta \end{array}}$

La condición de continuidad de la función de onda y de la derivada primera en x=a₀δ se expresa

${\displaystyle \{\begin{array}{l}{B}_1\sin \left(q{a}_0\delta \right)=B_2\frac{\delta }{\beta }\exp \left(-\frac{\delta }{\beta }\right)U\left(1-\beta \mathrm{,2};\frac{2\delta }{\beta }\right)\\ B_{1}q\cos \left(q{a}_0\delta \right)=\frac{B_2}{a_0\beta }\exp \left(-\frac{\delta }{\beta }\right)\left\{\left(1-\frac{\delta }{\beta }\right)U\left(1-\beta \mathrm{,2};\frac{2\delta }{\beta }\right)-2\left(1-\beta \right)\frac{a_0\delta }{a_0\beta }U\left(2-\beta \mathrm{,3};\frac{2\delta }{\beta }\right)\right\}\end{array}}$

Dividiendo la segunda entre la primera, obtenemos una ecuación trascendente, cuyas raíces nos dan los valores de β, o los niveles de energía E_n

${\displaystyle \frac{q{a}_0\delta }{\tan \left(q{a}_0\delta \right)}=1-\frac{\delta }{\beta }-2\left(1-\beta \right)\frac{\delta }{\beta }\frac{U\left(2-\beta \mathrm{,3};\frac{2\delta }{\beta }\right)}{U\left(1-\beta \mathrm{,2};\frac{2\delta }{\beta }\right)},q{a}_0=\sqrt{\frac{2}{\delta }-\frac{1}{{\beta }^2}}}$

que transformamos para realizar el cálculo numérico de forma adecuada

${\displaystyle q{a}_0\delta \beta \cos \left(q{a}_0\delta \right)U\left(1-\beta \mathrm{,2};\frac{2\delta }{\beta }\right)-\cos \left(q{a}_0\delta \right)\left\{\left(\beta -\delta \right)U\left(1-\beta \mathrm{,2};\frac{2\delta }{\beta }\right)-2\delta \left(1-\beta \right)U\left(2-\beta \mathrm{,3};\frac{2\delta }{\beta }\right)\right\}}$

Calculamos los valores de β para δ=10^-3

function hipergeometrica_9   
    delta=1e-3;
    x=linspace(0,4.5,50);
    rImpar=raices(@impar,x);
    disp(rImpar)
    hold on
    fplot(@impar,[0,4.5])
    for j=1:length(rImpar)
          plot(rImpar(j),0, 'bo','markersize',3,'markerfacecolor','b')
    end
    hold off
    grid on
    ylim([-300,300])
    xlabel('x/a_0')
    ylabel('f(x)')
    title('Raíces de la ecuación transcendente')

     function res=impar(x)
         q=sqrt(2/delta-1./x.^2);
         u_2=kummerU(1-x,2,2*delta./x);
         u_3=kummerU(2-x,3,2*delta./x);
        res=((x-delta).*u_2-2*delta*(1-x).*u_3).*sin(q*delta)-delta*(x.*u_2).
*(q.*cos(q*delta));
     end

    function r = raices(f, x)
        y=f(x);
        indices=find(y(1:end-1).*y(2:end)<0);
        r=zeros(1,length(indices));
        for k=1:length(indices)
            r(k)=fzero(f, [x(indices(k)), x(indices(k)+1)]);
        end
     end
end

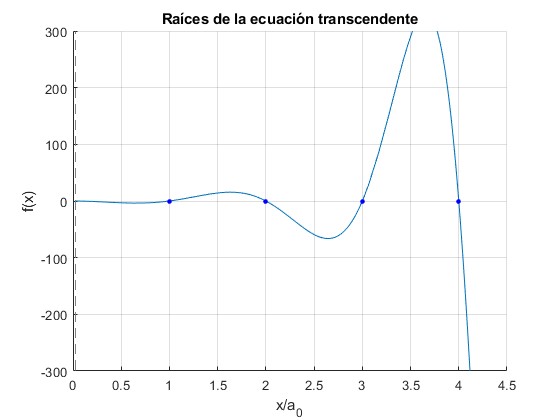
   1.0000    2.0000    3.0000    4.0000

Representamos las raíces mediante puntos de color azul

Funciones de onda

${\displaystyle \begin{array}{l}\psi (x)=\{\begin{array}{l}{B}_1\sin \left(qx\right),x<a_0\delta \\ B_2\frac{x}{a_0\beta }\exp \left(-\frac{x}{a_0\beta }\right)U\left(1-\beta \mathrm{,2};\frac{2x}{a_0\beta }\right),x\ge a_0\delta \end{array}\\ B_1\sin \left(q{a}_0\delta \right)=B_2\frac{\delta }{\beta }\exp \left(-\frac{\delta }{\beta }\right)U\left(1-\beta \mathrm{,2};\frac{2\delta }{\beta }\right)\end{array}}$

La última expresión relaciona los coeficientes B₁ y B₂

Por razones de simetría se deberá cumplir que

${\displaystyle {\displaystyle \underset{0}{\overset{\infty }{\int }}{\left|\psi (x)\right|}^{2}dx=\frac{1}{2}}}$

Lo que nos permite determinar B₁

${\displaystyle B_1^2{\displaystyle \underset{0}{\overset{a_0\delta }{\int }}{\sin }^2\left(qx\right)dx+\frac{B_2^2}{{\left(a_0\beta \right)}^2}}{\displaystyle \underset{a_0\delta }{\overset{\infty }{\int }}{x}^2\exp \left(-\frac{2x}{a_0\beta }\right)U^2\left(1-\beta \mathrm{,2};\frac{2x}{a_0\beta }\right)}dx=\frac{1}{2}}$

Haciendo el cambio de variable, z=x/(a₀δ)

${\displaystyle B_1^2{a}_0\delta \left\{\frac{1}{2}\left(1-\frac{\sin \left(2q{a}_0\delta \right)}{2q{a}_0\delta }\right)+\frac{{\sin }^2\left(q{a}_0\delta \right)}{\exp \left(-\frac{2\delta }{\beta }\right)U^2\left(1-\beta \mathrm{,2};\frac{2\delta }{\beta }\right)}{\displaystyle \underset{1}{\overset{\infty }{\int }}{z}^2\exp \left(-\frac{2\delta }{\beta }z\right)U^2\left(1-\beta \mathrm{,2};\frac{2\delta }{\beta }z\right)}dz\right\}=\frac{1}{2}}$

Despejamos B₁ y calculamos B₂

Representamos las funciones de onda para los niveles β=1.0000, 2.0000, 3.0000, que hemos calculado para δ=10^-3. Comprobamos que la función de onda es continua para x/a₀=10^-3

delta=1e-3;
 for beta=[1.0,2.0,3.0]
     f=@(x) x.*exp(-x*delta/beta).*kummerU(1-beta,2,2*delta*x/beta);
     g=@(x) f(x).^2;
     area1=integral(g,1,20);
     q=sqrt(2/delta-1/beta^2);
     area=(1-sin(2*q*delta)/(2*q*delta))/2+sin(q*delta)^2*area1/(exp(-2*delta/beta)
*kummerU(1-beta,2,2*delta/beta)^2);
     B1=sqrt(0.5/(delta*area));
     B2=B1*sin(q*delta)*beta/(delta*exp(-delta/beta)*kummerU(1-beta,2,2*delta/beta));
     hold on
     f1=@(x) B1*sin(q*x);
     fplot(f1 ,[0,delta])
     f2=@(x) B2*(x.*exp(-x/beta)).*kummerU(1-beta,2,2*x/beta)/beta;
     fplot(f2, [delta, 25])
 end
 hold off
 grid on
 xlabel('x/a_0')
 xlim([0,3*delta])
 ylabel('\Psi(x)')
 title('Funciones de onda')

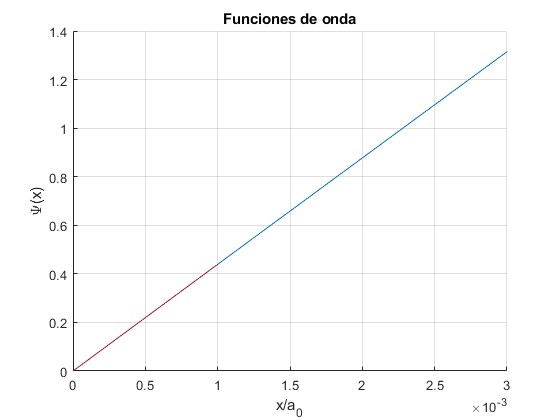
Representamos la función de onda hasta x/a₀=25, anulando la sentencia xlim([0,3*delta])

Niveles de energía

Reprentamos los niveles de energía β en función de 1/ln(1/δ) para δ=10^-2, 10^-3, 10^-4, 10^-5, 10^-6 y 10^-7

• mediante puntos de color rojo, que da lugar a una función de onda simétrica
• mediante puntos de color azul, que da lugar a una función de onda antisimétrica

function hypergeometrica_3
    x=linspace(0,5,60);
    hold on
    for k=2:7 
        delta=1/10^k;
         rPar=raices(@par, x);
        rImpar=raices(@impar, x);
        for j=1:length(rPar)
           plot(1/log(1/delta),rPar(j),'ro','markersize',3,'markerfacecolor','r')
        end
        for j=1:length(rImpar)
           plot(1/log(1/delta),rImpar(j),'bo','markersize',3,'markerfacecolor','b')
        end
    end
    hold off
    xlabel('1/ln(1/\delta)')
    ylabel('\beta')
    title('Niveles de energía')
    grid on 
    
    function res=par(x)
         q=sqrt(2/delta-1./x.^2);
         u_2=kummerU(1-x,2,2*delta./x);
         u_3=kummerU(2-x,3,2*delta./x);
        res=((x-delta).*u_2-2*delta*(1-x).*u_3).*cos(q*delta)+delta*(x.*u_2).
*(q.*sin(q*delta));
     end
     function res=impar(x)
         q=sqrt(2/delta-1./x.^2);
         u_2=kummerU(1-x,2,2*delta./x);
         u_3=kummerU(2-x,3,2*delta./x);
        res=((x-delta).*u_2-2*delta*(1-x).*u_3).*sin(q*delta)-delta*(x.*u_2).
*(q.*cos(q*delta));
     end

     function r = raices(f, x)
        y=f(x);
        indices=find(y(1:end-1).*y(2:end)<0);
        r=zeros(1,length(indices));
        for k=1:length(indices)
            r(k)=fzero(f, [x(indices(k)), x(indices(k)+1)]);
        end
     end
 end

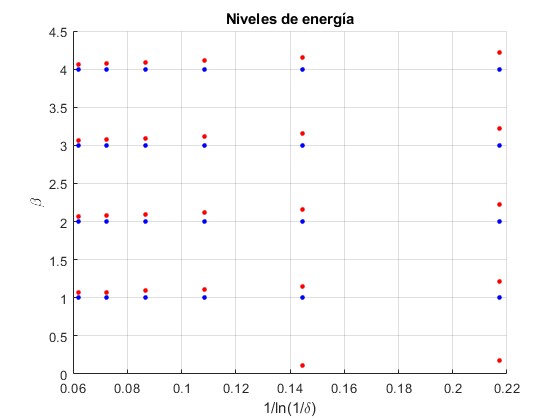
En la tabla se recogen los valores numéricos de los puntos de la gráfica para distintos valores de δ

El símbolo ? indica que no se ha podido calcular el nivel de energía

Referencias

Rufus Boyack, Frank Marsiglio. The bound-state solutions of the one-dimensional hydrogen atom. Am. J. Phys. 89 (4), April 2021, pp. 418-425