Braquistócrona en una superficie cilíndrica y esférica
Superficie cilíndrica
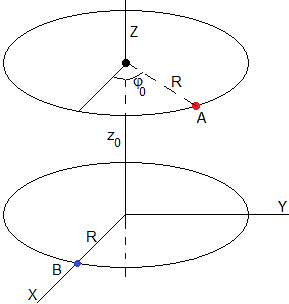
Supongamos que una partícula parte en reposo de un punto A (R, φ0, z0) situado en la superficie cilíndrica a una altura z0, formando un ángulo φ0 con el eje X y llega al punto B (R, 0, 0) situado en el eje X, tal como se muestra en la figura.
Aplicamos el principio de conservación de la energía, para calcular la velocidad de la partícula cuando está a una altura z
Las coordenadas de un punto sobre la superficie cilíndrica son,
x=Rcosφ, y=Rsinφ, z
El desplazamiento infinitesimal ds a lo largo de una línea contenida en dicha superficie
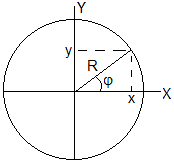
El tiempo que emplea la partícula en desplazarse desde A a B es
Aplicamos la ecuación de Euler-Lagrange a la función f que no depende de φ
por lo que utilizamos la segunda versión de dicha ecuación
Donde C es una constante. Elevamos al cuadrado, despejamos , e integramos respecto de z
Nota: Las raíces de la ecuación x2=k2, son x=±k. Habitualmente, tomamos el signo positivo, pero hay ocasiones en que el resultado es un número negativo
Donde c es una constante. Haciendo el cambio de variable, y=z0-z, dy=-dz
Donde k es una constante a determinar. Hacemos el cambio de variable
El resultado es
Cuando el parámetro θ=0, φ=φ0. La otra ecuación viene del cambio de variable
Cuando el parámetro θ=0, z=z0
Un resultado similar al obtenido para la braquistócrona en el plano vertical
Las ecuaciones paramétricas de la trayectoria son
Vamos a determinar el valor de la constante k y del parámetro θ cuando la partícula llega a la posición final B (R,0,0), resolviendo el sistema de dos ecuaciones
Dividimos la segunda entre la primera
Calculamos la raíz θ1 de la ecuación transcendente. De la segunda ecuación, despejamos k.
Tiempo mínimo
Calculamos el tiempo mínimo que emplea la partícula en desplazarse desde A a B a lo largo de dicha trayectoria
De las expresiones de z y φ en términos del parámetro θ
El resultado debería dar un número positivo
Tiempo geodésica
Calculamos el tiempo que emplea la partícula en desplazarse de A a B a lo largo de la geodésica que une ambos puntos.
En la página titulada Líneas geodésicas, demostramos que para una superficie cilíndrica son líneas helicoidales de paso constante, de ecuación φ=c3z+c2. Donde las constantes c2 y c3 se determinan a partir de las coordenadas de los puntos A y B
φ0=c3z0+c2
0=c3·0+c2
La ecuación de la línea helicoidal sobre la superficie cilíndrica que pasa por A y B es
Expresamos z y su derivada en términos del ángulo φ
Es una integral inmediata que se resuelve haciendo el cambio de variable u=1-φ/φ0, du=-dφ/φ0. El resultado es
Resultados
Sea una superficie cilíndrica de radio R=1, la posición inicial A es (z0=12, φ0=4π). La posición final B es (z=0, φ=0)
Representamos la función transcendente para localizar las raíz θ1
R=1; %radio
z0=12; %posición inicial A
phi_0=4*pi;
f=@(x) 2*R*phi_0*sin(x).^2-z0*(2*x-sin(2*x));
fplot(f,[0,pi])
xlabel('\theta')
ylabel('f(\theta)')
grid on
title('Ecuación transcendente')
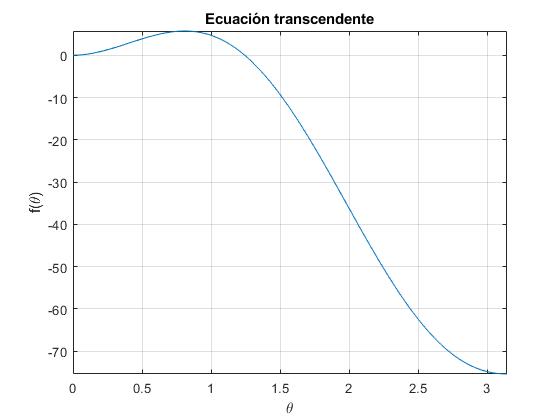
La raíz buscada θ1 estará comprendida entre θ=1 y 1.5 rad. Utilizamos la función
- φ0=4π
- φ0=6π
- φ0=8π
R=1; %radio
z0=12; %posición inicial A
for phi_0=[4,6,8]*pi
f=@(x) 2*R*phi_0*sin(x).^2-z0*(2*x-sin(2*x));
th_1=fzero(f,[0.2,2]);
k=z0/sin(th_1)^2;
Tm=2*th_1/sin(th_1); %en unidades de tiempo de caída libre
Tg=2*sqrt((R*phi_0/z0)^2+1);
fprintf('posición, %1.3f, tiempo mínimo, %1.3f, tiempo geodésica,
%1.3f\n',phi_0, Tm,Tg)
end
posición, 12.566, tiempo mínimo, 2.626, tiempo geodésica, 2.896 posición, 18.850, tiempo mínimo, 3.142, tiempo geodésica, 3.724 posición, 25.133, tiempo mínimo, 3.661, tiempo geodésica, 4.642
| φ0 | Tm | Tg |
|---|---|---|
| 4π | 2.626 | 2.896 |
| 6π | 3.142 | 3.724 |
| 8π | 3.661 | 4.642 |
Comprobamos que Tg es mayor que Tm
Representamos la trayectoria (color rojo) y la geodésica (color negro) para los tres valores del ángulo inicial φ0
R=1; %radio
z0=12; %posición inicial A
phi_0=4*pi; %cambiar 6*pi y 8*pi
f=@(x) 2*R*phi_0*sin(x).^2-z0*(2*x-sin(2*x));
th_1=fzero(f,[0.2,2]);
k=z0/sin(th_1)^2;
Tm=2*th_1/sin(th_1);
Tg=2*sqrt((R*phi_0/z0)^2+1);
hold on
r=1*ones(30,1);
phi=linspace(0,2*pi,30);
[r,phi]=meshgrid(r,phi);
x=r.*cos(phi);
y=r.*sin(phi);
z=repmat(linspace(-1,12.5,30),30,1);
surfl(x,y,z);
shading interp
colormap([0.5 0.5 0.5]);
%espiral
th=linspace(0,th_1,400);
phi=-k*(th-sin(2*th)/2)/R+phi_0;
z=z0-k*sin(th).^2;
plot3(cos(phi),sin(phi),z, 'r','lineWidth',1.5)
phi=linspace(0,phi_0,400);
z=z0*phi/phi_0;
plot3(cos(phi),sin(phi),z, 'k')
hold off
axis equal
xlabel('x'); ylabel('y'); zlabel('z')
title('Superficie cilíndrica')
view(60,15)
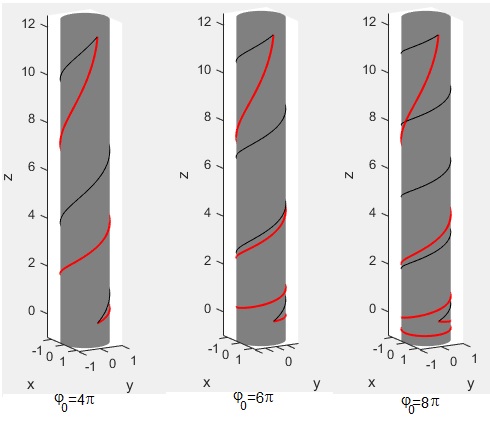
Para ver mejor las trayectorias eliminamos el cilindro de color gris
R=1; %radio
z0=12; %posición inicial A
phi_0=4*pi;
f=@(x) 2*R*phi_0*sin(x).^2-z0*(2*x-sin(2*x));
th_1=fzero(f,[0.2,2]);
k=z0/sin(th_1)^2;
Tm=2*th_1/sin(th_1);
Tg=2*sqrt((R*phi_0/z0)^2+1);
hold on
%espiral
th=linspace(0,th_1,400);
phi=-k*(th-sin(2*th)/2)/R+phi_0;
z=z0-k*sin(th).^2;
plot3(cos(phi),sin(phi),z, 'r','lineWidth',1.5)
phi=linspace(0,phi_0,400);
z=z0*phi/phi_0;
plot3(cos(phi),sin(phi),z, 'k')
hold off
axis equal
xlabel('x'); ylabel('y'); zlabel('z')
title('Superficie cilíndrica')
view(60,15)
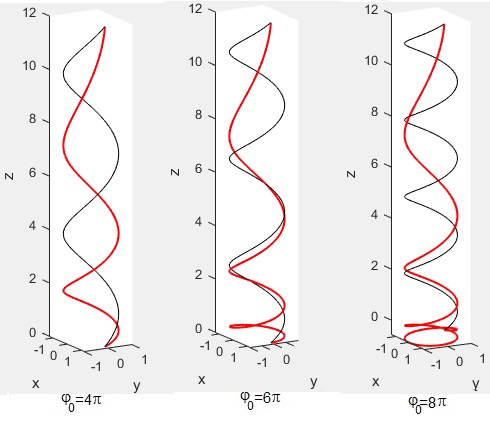
Observamos que la partícula, en los primeros instantes, cae casi verticalmente, luego, describe la hélice de paso variable. Lo más sorpendente, es que en el tercer caso, φ0=8π, la partícula se mueve por debajo del origen z<0 y luego, regresa a la posición final z=0. Parece mucho rodeo para un tiempo mínimo. Como podemos comprobar, la posición final B (z=0) se alcanza para el valor del parámetro θ1=1.7875 y tambien, para π-θ1=1.3541 (antes)
Estos tres casos se corresponden, con los tres mencionados en el caso del plano vertical
Superficie esférica
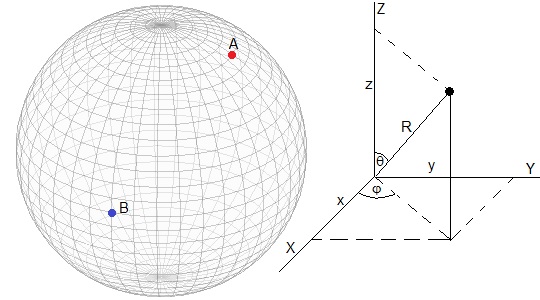
Supongamos que una partícula parte en reposo de un punto A (φ0, θ0) situado en la superficie esférica de radio R a una altura z0=Rcosθ0 y llega al punto B (φ1, θ1) tal como se muestra en la figura.
Aplicamos el principio de conservación de la energía, para calcular la velocidad de la partícula cuando está a una altura z
Las coordenadas de un punto sobre la superficie esférica son
x=Rcosφ·sinθ, y=Rsinφ·sinθ, z=Rcosθ
El desplazamiento infinitesimal ds a lo largo de una línea contenida en dicha superficie
El tiempo que emplea la partícula en desplazarse desde A a B es
Aplicamos la ecuación de Euler-Lagrange a la función f que no depende de φ
por lo que utilizamos la segunda versión de dicha ecuación
Donde C es una constante. Elevamos al cuadrado, despejamos e integramos respecto de θ
Donde c es una constante a determinar de modo que se alcance la posición final B (φ1, θ1)
Utilizaremos la función
Conocida la constante c, determinamos la trayectoria mediante la ecuación φ-φ0=f(θ)
Tiempo mínimo
Conocida la constante c calculamos el tiempo mínimo Tm que emplea la partícula en desplazarse a la largo de dicha trayectoria entre A y B
Tiempo geodésica
Calculamos el tiempo que emplea la partícula en desplazarse de A a B a lo largo de la geodésica que une ambos puntos.
En la página titulada Líneas geodésicas, determinamos la ecuación de la línea geodésica sobre una superficie esférica de radio R que pasa por los puntos A y B
La ecuación es
Damos valores a φ entre 0 y 2π, obtenemos el ángulo θ, dibujamos el punto de coordenadas (φ, θ), unimos los puntos para trazar la circunferencia máxima que pasa por A y B
Despejamos el ángulo φ para calcular la derivada dφ/dθ y obtener el tiempo que emplea la partícula en desplazarse desde A a B a través de la geodésica que pasa por dichos puntos
El tiempo Tg es
Resultados
Sea una superficie esférica de radio R=1, la posición inicial A es (φ0=π/3, θ0=π/6). La posición final B es (φ1=π/10, θ0=2π/5)
Representamos la función transcendente, φ1-φ0±f(c), para localizar la intersección con el eje X (cero(s)). El signo puede ser positivo o negativo
Utilizamos la función
fzero de MATLAB para obtener una mejor aproximación de la constante cCalculamos el tiempo mínimo Tm y el tiempo Tg a lo largo de la geodésica que une los puntos A y B.
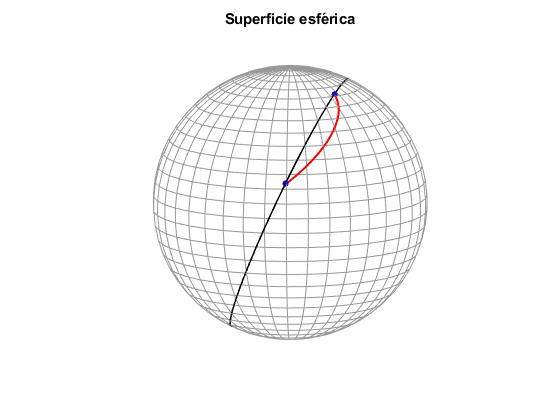
Representamos la trayectoria (color rojo) y la geodésica (negro) que pasa por los puntos A y B
phi_0=pi/3; %posición A
th_0=pi/6;
phi_1=pi/10; %posición B
th_1=2*pi/5;
cc=0:0.01:1.4;
res=zeros(1, length(cc));
i=1;
for c=cc
f=@(x) sqrt((cos(th_0)-cos(x))./(c*sin(x).^4-sin(x).^2.*
(cos(th_0)-cos(x))));
res(i)=phi_1-phi_0+integral(f,th_0, th_1);
i=i+1;
end
plot(cc,res)
grid on
xlabel('c')
ylabel('f(c)')
title('Constante c')
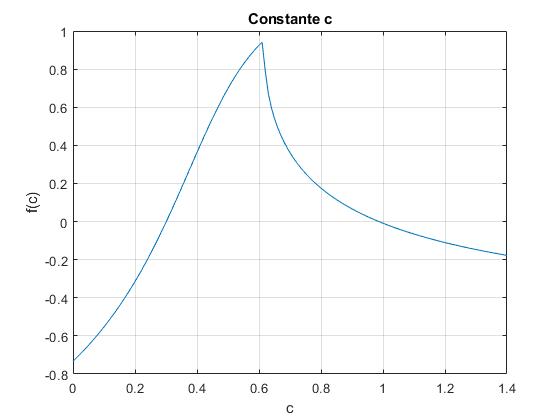
Hay dos posibles valores de c uno próximo a 0.3 y otro próximo a 1. Descartamos el primero ya que obtenemos un valor complejo del tiempo Tm.
phi_0=pi/3; th_0=pi/6; phi_1=pi/10; th_1=2*pi/5; f=@(x,c) sqrt((cos(th_0)-cos(x))./(c*sin(x).^4-sin(x).^2.* (cos(th_0)-cos(x)))); g=@(c) phi_1-phi_0+integral(@(x) f(x,c),th_0, th_1); c=fzero(g,[0.8,1.2]); disp(c)
0.9867
R=1; %radio phi_0=pi/3; %posición A th_0=pi/6; phi_1=pi/10; %posición B th_1=2*pi/5; %tiempo mínimo c=0.9867; %constante c f=@(x) sin(x)./sqrt((cos(th_0)-cos(x)).*(c*sin(x).^2-cos(th_0)+cos(x))); Tm=sqrt(c*R/(2*9.8))*integral(f,th_0,th_1); %tiempo geodésica x0=cos(phi_0)*sin(th_0); y0=sin(phi_0)*sin(th_0); z0=cos(th_0); x1=cos(phi_1)*sin(th_1); y1=sin(phi_1)*sin(th_1); z1=cos(th_1); A=atan2((y0*z1-y1*z0),(x0*z1-x1*z0)); B=(x0*sin(A)-y0*cos(A))/z0; g=@(x) sin(x)./sqrt((sin(x).^2-B^2*cos(x).^2).*(cos(th_0)-cos(x))); Tg=sqrt(R/(2*9.8))*sqrt(B^2+1)*integral(g,th_0,th_1); disp([Tm,Tg])
0.5997 0.6840
Comprobamos que el tiempo a lo largo de la línea geodésica es mayor
%esfera
phi=linspace(0,pi,30);
theta=linspace(0,2*pi,40);
[phi,theta]=meshgrid(phi,theta);
x=sin(phi).*cos(theta);
y=sin(phi).*sin(theta);
z=cos(phi);
hold on
h1=mesh(x,y,z);
set(h1,'EdgeColor',[0.6,0.6,0.6]);
%punto A
phi_0=pi/3;
th_0=pi/6;
x0=cos(phi_0)*sin(th_0);
y0=sin(phi_0)*sin(th_0);
z0=cos(th_0);
plot3(x0,y0,z0,'o','markersize',4,'markeredgecolor','b','markerfacecolor','b')
%punto B
phi_1=pi/10;
th_1=2*pi/5;
x1=cos(phi_1)*sin(th_1);
y1=sin(phi_1)*sin(th_1);
z1=cos(th_1);
plot3(x1,y1,z1,'o','markersize',4,'markeredgecolor','b','markerfacecolor','b')
%trayectoria
c=0.9876; %constante
thh=linspace(th_0,th_1,50);
phi=zeros(1,length(thh));
i=1;
for th=thh
f=@(x) sqrt((cos(th_0)-cos(x))./(c*sin(x).^4-sin(x).^2.*
(cos(th_0)-cos(x))));
phi(i)=phi_0-integral(f,th_0,th);
i=i+1;
end
plot3(cos(phi).*sin(thh),sin(phi).*sin(thh),cos(thh),'r','lineWidth',1.5)
%geodésica
A=atan2((y0*z1-y1*z0),(x0*z1-x1*z0));
B=(x0*sin(A)-y0*cos(A))/z0;
phi=(0:360)*pi/180;
th=atan2(B,sin(A-phi));
plot3(cos(phi).*sin(th),sin(phi).*sin(th),cos(th), 'k','lineWidth',1)
axis equal
axis off
view(110,10)
hold off
xlabel('x'); ylabel('y'); zlabel('z')
title('Superficie esférica')
Conclusiones
El cálculo numérico con MATLAB es muy complejo y produce errores y avisos en muchas ocasiones, se vuelve inestable. Quizás algún lector interesado pueda encontrar la solución a los distintos casos
Referencias
H. A. Yamani, A. A. Mulhem. A cylindrical variation on the brachistochrone problem. Am. J. Phys. 56 (5) May 1988, pp. 467-469
Rafael Xavier Deiga Ferreira, Hector Leny Carrion Salazar. Braquistócrona na esfera. Revista Brasileira de Ensino de Física, vol. 41, n° 4, e20190020 (2019). https://www.scielo.br/j/rbef/i/2019.v41n4/

