La corriente inducida

En la figura, se representa la situación inicial de las espiras del galvanómetro, justo en el momento en el que ha adquirido una velocidad angular inicial w₀, después de haber pasado la corriente.

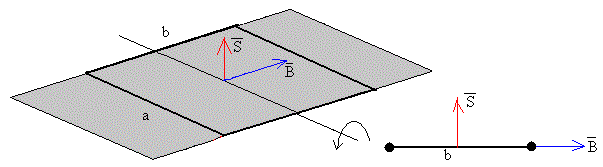
En esta otra figura, se representa la corriente inducida en las espiras cuando su plano ha girado un ángulo θ respecto del plano horizontal.

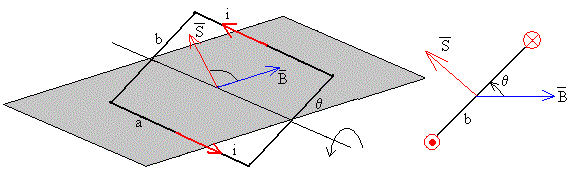
El flujo del campo magnético que atraviesa las N espiras de área S es

${\displaystyle \Phi =\overrightarrow{B}·N\overrightarrow{S}=NBS\cos (90+\theta )=-NBS\sin \theta }$

De acuerdo con la ley de Faraday la fem vale

${\displaystyle V_{\epsilon }=-\frac{d\Phi }{dt}=NBS\cos \theta ·\frac{d\theta }{dt}}$

El sentido de la corriente inducida i se obtiene aplicando la ley de Lenz. Como el flujo Φ aumenta la corriente inducida se opone al aumento de flujo. Las flechas de color rojo indican el sentido de dicha corriente.

${\displaystyle i=\frac{V_{\epsilon }}{R}=\frac{NBS}{R}\cos \theta ·\frac{d\theta }{dt}}$

Siendo R la resistencia del circuito

Fuerzas y momento que ejerce el campo magnético

El campo magnético ejerce una fuerza y un momento sobre las espiras. Como ya demostramos solamente es necesario determinar las fuerzas sobre los lados de longitud a de la espira.

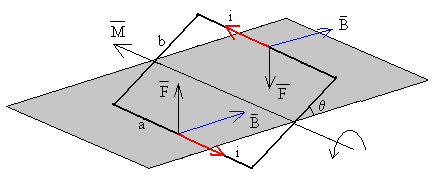
El módulo de la fuerza sobre cada uno de los lados es

F=iNBa

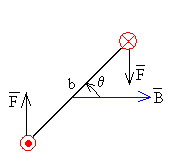
Tiene la dirección y el sentido mostrado en la figura.

El momento de dichas fuerzas respecto del eje de rotación es

M=-2F(b/2)cosθ =i·NBS·cosθ

${\displaystyle M=-\frac{N^2{B}^2{S}^2}{R}{\cos }^2\theta ·\frac{d\theta }{dt}}$

Este momento se opone a la velocidad de rotación de las espiras.

Ecuación del movimiento

El momento total que se ejerce sobre la bobina es la suma del momento que ejerce el campo magnético M y del momento que ejerce el muelle helicoidal -k·θ , tal como vimos en el estudio previo del galvanómetro balístico. Donde k es la constante del muelle helicoidal o la constante de torsión del hilo.

La ecuación de la dinámica de rotación es (Momento de inercia por aceleración angular igual al momento de las fuerzas que se ejercen sobre el sólido).

${\displaystyle \begin{array}{l}I\alpha =M-k\theta \\ I\frac{d^2\theta }{d{t}^2}=-k\theta -\frac{N^2{B}^2{S}^2}{R}{\cos }^2\theta ·\frac{d\theta }{dt}\end{array}}$

En forma de ecuación diferencial

${\displaystyle \frac{d^2\theta }{d{t}^2}+\frac{N^2{B}^2{S}^2}{I·R}{\cos }^2\theta ·\frac{d\theta }{dt}+\frac{k}{I}\theta =0}$

Se trata de una ecuación similar a la ecuación diferencial que describe las oscilaciones amortiguadas salvo el término cos² θ, que multiplica a la derivada primera dθ/dt

Si el ángulo θ es pequeño, tomamos cos²θ ≈ 1

${\displaystyle \frac{d^2\theta }{d{t}^2}+\frac{N^2{B}^2{S}^2}{I·R}\frac{d\theta }{dt}+\frac{k}{I}\theta \approx 0}$

Tenemos una oscilación amortiguada cuya frecuencia propia es

${\displaystyle {\omega }_0=\sqrt{\frac{k}{I}}}$

y cuya constante de amortiguación

${\displaystyle \gamma =\frac{N^2{B}^2{S}^2}{2IR}}$

La frecuencia de la oscilación amortiguada es

${\displaystyle \omega =\sqrt{{\omega }_0^2-{\gamma }^2}}$

y la solución de la ecuación diferencial es la ecuación de la oscilación amortiguada

${\displaystyle \theta =A\exp (-\gamma ·t)\sin \left(\omega t+\phi \right)}$

La característica esencial de una oscilación amortiguada es que su amplitud disminuye exponencialmente con el tiempo.

Si la resistencia R es grande, el factor de amortiguamiento γ es pequeño y la oscilación disminuye poco a poco su amplitud con el tiempo. Si la resistencia R es pequeña, el factor γ es grande y la amplitud decrece rápidamente.

La amplitud A y la fase inicial φ se determinan a partir de las condiciones iniciales, en el instante t=0, θ =0, ${\left(\frac{d\theta }{dt}\right)}_{t=0}=w_0$

donde w₀ ( no confundir con la frecuencia propia ω₀) es la velocidad angular inicial que proporciona el impulso angular de la corriente que atraviesa el galvanómetro.

${\displaystyle \theta =\frac{w_0}{\omega }\exp (-\gamma ·t)\sin \left(\omega t\right)}$

En el caso de que el desplazamiento θ  sea grande, ya no podremos hacer la aproximación cos²θ ≈ 1, y la ecuación diferencial ha de resolverse de forma numérica.

Simplificamos la ecuación diferencial tomando la escala de tiempos

${\displaystyle t=\tau \sqrt{\frac{I}{k}}}$

La ecuación diferencial resultante depende de un parámetro a

${\displaystyle \frac{d^2\theta }{d{\tau }^2}+a{\cos }^2\theta ·\frac{d\theta }{d\tau }+\theta =0a=\frac{N^2{S}^2{B}^2}{R\sqrt{I·k}}}$

Si la resistencia R es grande el factor a es pequeño y la oscilación cambia poco su amplitud con el paso del tiempo. Si la resistencia R es pequeña el factor a es grande y la oscilación desaparece rápidamente, regresando el galvanómetro a la posición inicial de partida.

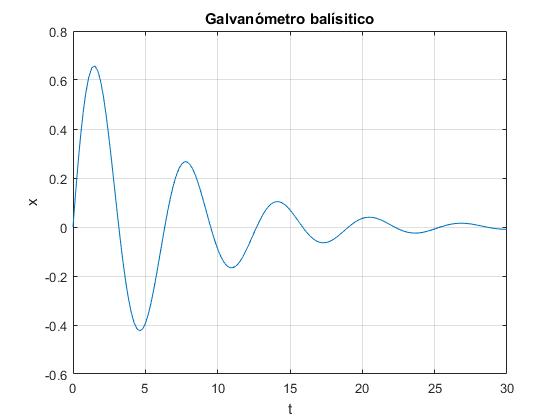
Resolvemos la ecuación diferencial por procedimientos numéricos asignando al parámetro a=0.2, con las condiciones iniciales siguientes: en el instante τ=0, la posición inicial es θ=0, y la velocidad inicial dθ/dτ=0.8

a=0.3; %parámetro
x0=[0,0.8]; %velocidad inicial
f=@(t,x) [x(2);-a*cos(x(1))^2*x(2)-x(1)]; 
[t,x]=ode45(f,[0,30],x0);
plot(t,x(:,1))
xlabel('t')
ylabel('x');
title('Galvanómetro balísitico')
grid on

Actividades

Se introduce

• el valor del parámetro a, en el control titulado Amortiguamiento.
• la velocidad angular inicial  w₀ en el instante inicial t=0, en el control titulado Velocidad angular inicial.

En el caso de que el ángulo máximo de desviación supere los 45º, el programa no prosigue y nos invita a disminuir la velocidad angular inicial.

Lo primero que observamos en la simulación es la corriente que atraviesa el galvanómetro durante un intervalo de tiempo pequeño comparado con el periodo de la oscilación del galvanómetro. Dicha corriente se representa mediante puntos de color azul que se mueven a lo largo de la espira. El campo magnético B ejerce un momento sobre las espiras durante el breve intervalo de tiempo que dura el paso de la corriente.

Las espiras no cambian apreciablemente de posición durante este corto intervalo de tiempo. Pero un momento actuando durante un tiempo produce un impulso angular que modifica la velocidad angular de rotación de la bobina. La bobina adquiere una velocidad angular inicial w₀ (no confundir con la frecuencia propia ω₀ del oscilador) que es la que introducimos en el control titulado Velocidad angular inicial.

La bobina se desplaza hasta alcanzar la posición angular máxima, regresa al origen y así sucesivamente, describiendo una oscilación cuya amplitud va disminuyendo con el tiempo.

En la parte superior, observamos el gráfico de la desviación de la aguja indicadora θ del galvanómetro en función del tiempo t.

En la parte izquierda, se muestra una vista en dos dimensiones del galvanómetro, las corrientes entrantes y salientes en las espiras se representan mediante los símbolos habituales.

Se invita al lector a comprobar el sentido de la corriente inducida y la dirección y sentido de las fuerzas que ejerce el campo magnético. Dibujando representaciones bidimensionales como las siguientes

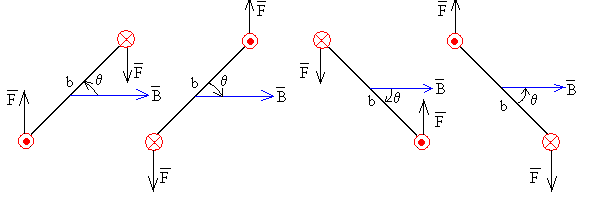
En la figura, vemos el sentido de la corriente inducida cada cuarto de periodo y las direcciones y sentidos de las fuerzas sobre cada lado de la espira. Comprobamos que el momento del par de fuerzas se opone siempre a la velocidad de rotación de la espira.

Referencias

Lim Yung-kuo. Problems and Solutions an Electromagnetism. World Scientific 1993, problem 2105, pp. 282-285.