Trayectorias elípticas (I)
Las leyes de Kepler
Las leyes de Kepler describen la cinemática del movimiento de los planetas en torno al Sol.
Primera ley
Los planetas describen órbitas elípticas estando el Sol en uno de sus focos
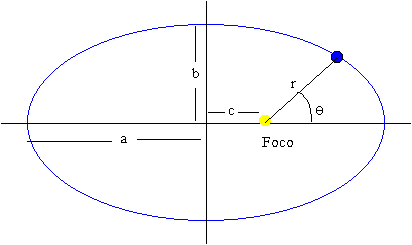
Segunda ley
El vector posición de cualquier planeta respecto del Sol, barre áreas iguales de la elipse en tiempos iguales.
La ley de las áreas es equivalente a la constancia del momento angular, es decir, cuando el planeta está más alejado del Sol (afelio) su velocidad es menor que cuando está más cercano al Sol (perihelio). En el afelio y en el perihelio, el momento angular L es el producto de la masa del planeta, por su velocidad y por su distancia al centro del Sol.
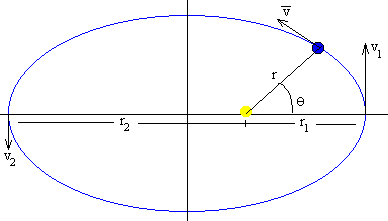
L=mr1·v1=mr2·v2
Tercera ley
Los cuadrados de los periodos P de revolución son proporcionales a los cubos de los semiejes mayores a de la elipse.
P2=k·a3
Como podemos apreciar, el periodo de los planetas depende solamente del eje mayor de la elipse. Los tres planetas de la animación tienen el mismo eje mayor 2a=6 unidades, por tanto, tienen el mismo periodo.
Geometría de la elipse
Como se ha descrito en la página Ecuación de la trayectoria otras páginas, una partícula sometida a una fuerza central atractiva, inversamente proporcional al cuadrado de la distancia al centro de fuerzas, describe una trayectoria elíptica si su energía total E<0 es negativa,
Los parámetros d y ε (excentricidad) están relacionados con el momento angular L y la energía E de la partícula
Una elipse es una cónica cuya excentricidad ε=c/a es menor que la unidad. Para que una partícula sometida a una fuerza central, atractiva, inversamente proporcional al cuadrado de las distancias al centro de fuerzas, describa dicha trayectoria tiene que tener una energía total negativa (E<0).
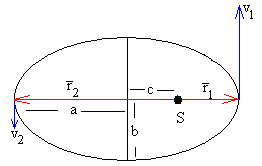
La posición más cercana al foco r1 se obtiene cuando θ=0 y la posición más alejada r2 se obtiene cuando θ=π. Es decir,
Los semiejes a y b de la elipse valen
El semieje mayor de la elipse a es independiente del momento angular L y solamente, depende de la energía total E. El semieje menor b depende del momento angular L y de la energía E
Ecuación de la elipse en coordenadas rectangulares
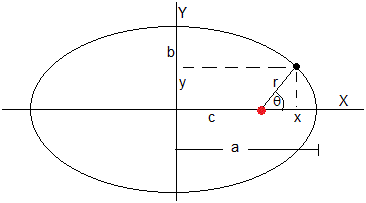
Dada la ecuación de la elipse en coordendas polares, vamos a deducir la ecuación de la elipse en coordendas rectangulares, estableciendo el origen del sistema de referencia en el centro de la elipse.
Partimos de la ecuación de la trayectoria en coordenadas polares
Las coordenadas rectangulares (x,y) del cuerpo celeste son:
x-c=r·cosθ
y=r·sinθ
La ecuación de la trayectoria se transforma en
Elevando al cuadrado
Teniendo en cuenta la relación entre el parámetro d y el semieje mayor de la elipse a, y la definición de excentricidad ε
La expresión anterior se simplifica notablemente y conduce a la ecuación de la elipse en coordenadas rectangulares
Periodo
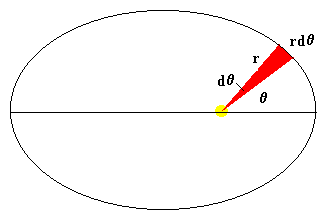
Se denomina periodo, al tiempo que tarda el móvil en dar una vuelta completa. En la figura vemos que el radio vector que une el Sol con el planeta barre en el intervalo de tiempo comprendido entre t y t+dt el área de color rojo de forma triangular.
El ángulo del vértice de dicho triángulo es dθ y la base del triángulo es un arco de longitud rdθ. El área del triángulo es (base por altura dividido por dos)
El vector posición de cualquier planeta respecto del Sol, barre áreas iguales de la elipse en tiempos iguales.
La ley de las áreas es equivalente a la constancia del momento angular, es decir, cuando el planeta está más alejado del Sol (afelio) su velocidad es menor que cuando está más cercano al Sol (perihelio). En el afelio y en el perihelio, el momento angular L es el producto de la masa del planeta, por su velocidad y por su distancia al centro del Sol.
Integrando la ecuación del momento angular expresado en coordenadas polares
La primera integral es el área total de la elipse πab, que es igual a la suma de las áreas de todos triángulos infinitesimales. La integral del segundo miembro es el periodo P del planeta, por tanto
Poniendo el semieje b en función del semieje a, (final del apartado anterior) llegamos a la fórmula que relaciona el periodo de la órbita de un planeta P y el semieje mayor de la elipse a, denominada tercera ley de Kepler.
Datos de los planetas
| Planeta | Semieje mayor (UA) | Excentricidad | Periodo (años) |
|---|---|---|---|
| Mercurio | 0.387 | 0.206 | 0.24 |
| Venus | 0.723 | 0.007 | 0.62 |
| Tierra | 1.000 | 0.017 | 1.00 |
| Marte | 1.524 | 0.093 | 1.88 |
| Júpiter | 5.203 | 0.048 | 11.86 |
| Saturno | 9.539 | 0.056 | 29.46 |
| Urano | 19.182 | 0.047 | 84.01 |
| Neptuno | 30.058 | 0.009 | 164.8 |
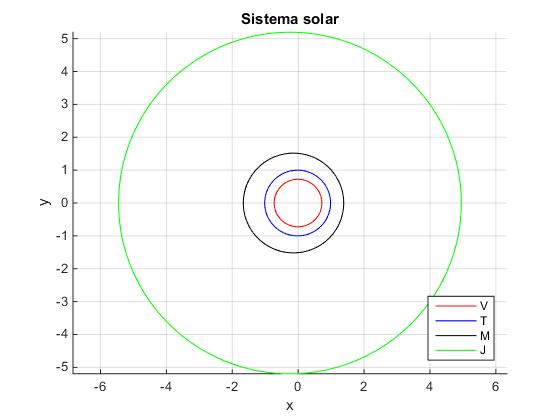
Escribimos un script para dibujar las órbitas elípticas de los planetas: Venus, Tierra, Marte y Júpiter conocidos sus ejes mayores en U.A. (Unidades Astronómicas) y sus excentricidades.
a=[0.723 1 1.524 5.203];
ex=[0.007 0.017 0.093 0.048];
ang=linspace(0,2*pi,100);
colores=['r' 'b' 'k' 'g'];
planeta=['V' 'T' 'M' 'J'];
hold on
for i=1:length(a)
d=a(i)*(1-ex(i)^2);
r=d./(1+ex(i)*cos(ang));
x=r.*cos(ang);
y=r.*sin(ang);
plot(x,y,colores(i),'displayName',planeta(i))
end
axis equal
grid on
xlabel('x')
ylabel('y')
title('Sistema solar')
legend('-DynamicLegend','location','SouthEast')
hold off
Relacionamos el semieje mayor de la trayectoria elíptica a con el periodo P. Representamos en el eje X, lna y en el eje Y, lnP. Los datos se ajustan a una línea recta, cuya pendiente determinamos.
a=[0.387,0.723,1,1.524,5.203,9.539,19.182,30.058]; %semieje mayor (UA)
P=[0.24,0.62,1,1.88,11.86,29.46,84.01,164.8]; %periodo (años)
plot(log(a),log(P), 'ro', 'markersize',4,'markeredgecolor' ,'r'
,'markerfacecolor','r')
xlabel('ln(a)')
ylabel('ln(P)')
grid on
title('Relación semieje mayor, periodo')
En el menú seleccionamos Tools/Basic Fitting, aparece un cuadro de diálogo donde marcamos la casilla linear debajo de Types of fit
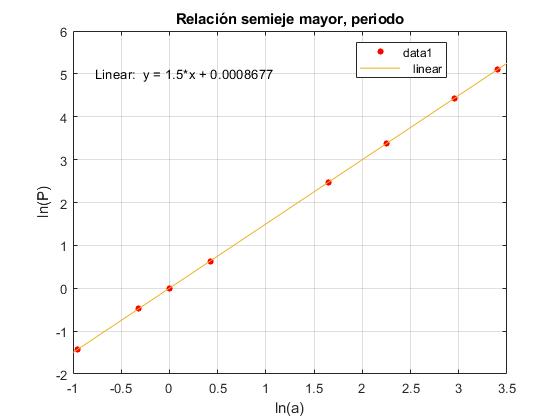
La pendiente de la recta es 3/2, lnP=3·lna/2 o bien,
Los cuadrados de los periodos P (en años) son iguales a los cubos del semieje mayor a (en unidades UA) de la elipse (Tercera ley de Kepler)
Ejemplo 1
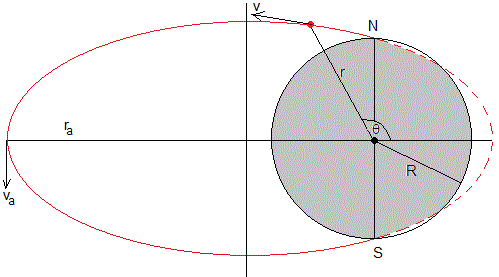
Se dispara un proyectil desde el polo Norte de la Luna con velocidad de v0=2200 m/s. Calcular el tiempo de vuelo. Datos
- Masa de la Luna, M=7.349·1022 kg
- Radio de la Luna, R=1737. 4 km
- Constante, G=6.67·10-11 N·m2/kg2
La ecuación de la elipse en coordenadas polares es
Para θ=π/2, r=R el radio de la Luna, por que el parámetro d=R.
El momento angular vale
La energía en la posición de disparo
Conocida la energía E y el momento angular L, calculamos la excentricidad ε
El semieje mayor a de la elipse es
El semieje menor b
Para calcular el tiempo empleado por el proyectil desde su disparo hasta que llega al punto de impacto, tenemos que determinar el área barrida por el radio vector, desde la posición inicial, π/2 a la final, 3π/2, el área A sombreada en la figura
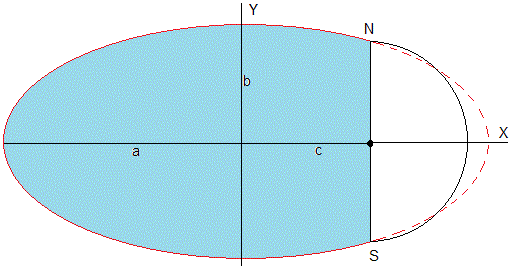
La ecuación de la elipse en coordenadas rectangulares es
La mitad A/2 del área sombreada es
Hacemos el cambio de variable, x=a·sinz, dx=a·cosz·dz
z1=-π/2, z2=arccos(c/a)=arccos(ε)
El tiempo de viuelo del proyectil entre el polo Norte y el polo Sur de la Luna es
R=1737.4*1000; %radio de la Luna M=7.349e22; %masa de la Luna G=6.67e-11; %constante G v0=2200; %velocidad de disparo E=v0^2/2-G*M/R; %energía L=sqrt(G*M*R); %momento angular ex=sqrt(v0^2*R/(G*M)-1); %excentricidad a=R/(1-ex^2); %semieje a b=a*sqrt(1-ex^2); %semieje b A=a*b*(asin(ex)+pi/2+ex*sqrt(1-ex^2)); %área T=2*A/sqrt(G*M*R); %tiempo disp(T)
El tiempo de vuelo del proyectil es T=41 309 s
4.1309e+04
Ejemplo 2
Este ejemplo se estudia la trayectoria de un proyectil disparado desde una altura h por encima de la Tierra en dirección perpendicular a la radial. El proyectil describe una órbita elíptica en uno de cuyos focos está el centro de la Tierra y en un plano perpendicular al ecuatorial chocando con la Tierra en un punto de latitud λ
En la página titulada Trayectoria de un proyectil disparado desde una altura h sobre la superficie de la Tierra se estudia este problema en profundidad
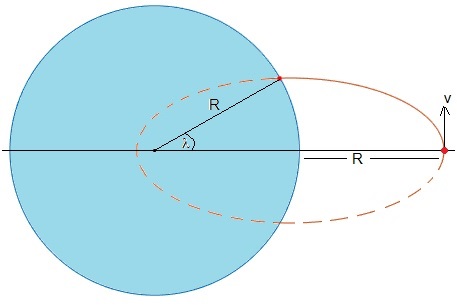
Para dibujar parte de esta figura se ha empleado el código
R=1; lambda=pi/6; alfa=sqrt((1-cos(lambda))/(2-cos(lambda))); e=1-alfa^2; d=2*alfa^2*R; hold on fplot(@(t) R*cos(t), @(t) R*sin(t),[0,2*pi]) ang=linspace(0,2*pi,180); r=d./(1+e*cos(ang)); x=2*d*e/(1-e^2)+r.*cos(ang); y=r.*sin(ang); plot(x,y) plot(R*cos(lambda),R*sin(lambda),'ro','markersize',3,'markeredgecolor','r', 'markerfacecolor','r') plot(0,0,'ko','markersize',2,'markeredgecolor','k','markerfacecolor','k') axis equal axis off
El proyectil de masa m se dispara desde una altura h=R igual al radio de la Tierra, en dirección perpendicular al radio vector, con velocidad.
Determinaremos el valor del parámetro α para que el proyectil impacte en una localidad del hemisferio norte situada a una latitud λ.
Recuérdese que el término que multiplica al parámetro α es la velocidad de un cuerpo celeste que describe una órbita circular de radio 2R. Aplicando la dinámica del movimiento circular uniforme
La energía y momento angular del proyectil es
La trayectoria es elíptica (E<0) si
La ecuación de la elipse en coordenadas polares es
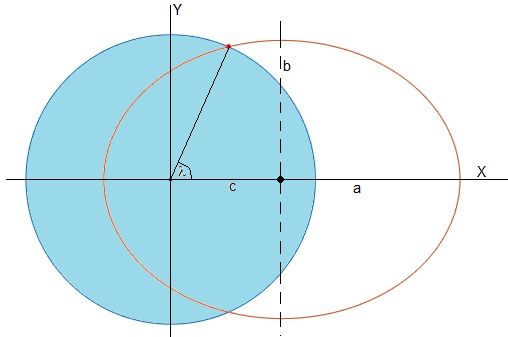
El semieje mayor a, menor b y semidistancia focal c son
Impacto del proyectil
Calculamos el punto de intersección de la elipse uno de cuyos focos es el centro de la Tierra y la circunferencia de radio R
Relacionamos el parámetro α con la latitud λ del punto de impacto
Supongamos que queremos que el proyectil impacte en una localidad del círculo polar ártico, λ=66.5°, el parámetro α=0.6128
Hay otro valor del parámetro α que da lugar a un impacto en el círculo polar ártico, la posición del punto de impacto es simétrica respecto del eje Y
El valor mínimo de α se obtiene para λ=0, α=0, caída libre del cuerpo. El valor máximo de α se obtiene para λ=π (180°),
Representamos tras trayectorias del proyectil para tres valores del parámero α=0.6128, 0.7636 y 0.8165
R=1; %radio
hold on
ang=linspace(0,2*pi,180);
fill(R*cos(ang),R*sin(ang),'c')
fplot(@(t) R*cos(t), @(t) R*sin(t),[0,2*pi], 'color','b')
for lambda=[66.5, -66.5, 180]*pi/180 %latitud
alfa=sqrt((1-sign(lambda)*cos(lambda))/(2-sign(lambda)*cos(lambda)));
ex=1-alfa^2; %excentricidad
d=2*alfa^2*R;
r=d./(1+ex*cos(ang));
x=2*d*ex/(1-ex^2)+r.*cos(ang);
y=r.*sin(ang);
plot(x,y)
plot(sign(lambda)*R*cos(lambda),sign(lambda)*R*sin(lambda),'ro',
'markersize',3,'markeredgecolor','r','markerfacecolor','r')
end
plot(0,0,'ko','markersize',2,'markeredgecolor','k','markerfacecolor','k')
hold off
axis equal
axis off
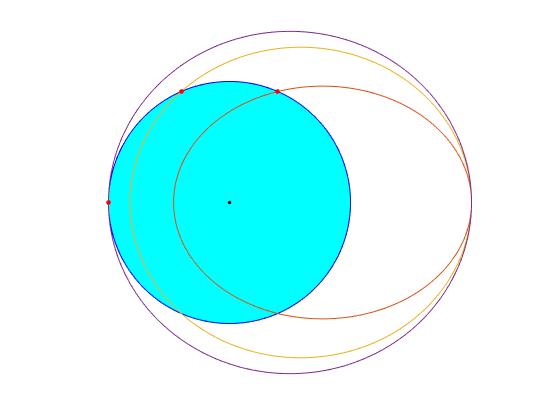
Tiempo que tarda el proyectil en llegar al punto de impacto
Para calcular el tiempo empleado por el proyectil desde su disparo hasta que llega al punto de impacto, tenemos que calcular el área barrida por el radio vector, desde la posición inicial a la final, el área sombreada en gris en la figura
Donde A se refiere al área barrida por el radio vector
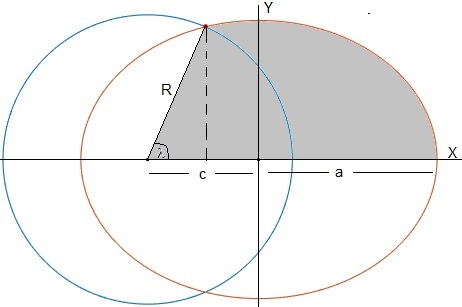
El área sombreada es la suma del área de un triángulo de base Rcosλ y altura Rsinλ y el área de la parte de elipse comprendida entre -c+Rcosλ y a.
El primer sumando vale
La ecuación de la elipse es
El segundo sumando vale
Hacemos el cambio de variable, x=a·sinz, dx=a·cosz·dz
El área total es
R=6.67e6; %radio de la Tierra M=5.98e24; %masa de la Tierra G=6.67e-11; %constante G lambda=66.5*pi/180; %latitud alfa=sqrt((1-cos(lambda))/(2-cos(lambda))); %parámetro ex=1-alfa^2; %excentricidad d=2*alfa^2*R; a=2*R/(2-alfa^2); %semieje mayor c=ex*a; %semidistancia focal b=sqrt(a^2-c^2); %semieje menor z1=asin((-c+R*cos(lambda))/a); area=R^2*sin(2*lambda)/4+a*b*(pi/2-z1-sin(2*z1)/2)/2; v=alfa*sqrt(G*M/(2*R)); T=2*area/(v*2*R); disp(T/60)
El proyectil tarda 48.5 minutos en llegar al punto de impacto
48.5392
Ejemplo 3
Sea un sistema solar formado por una estrella de masa M, un planeta en órbita circular de radio R y un cometa que describe una órbita elíptica de semeje mayor a y excentricidad ε, en el mismo plano
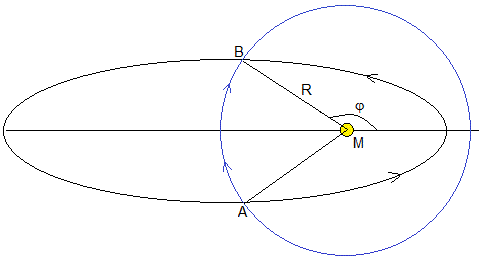
Vamos a determinar el radio R de la órbita del planeta para que se produzcan dos encuentros A y B con el cometa. El tiempo tAB que emplea el planeta en recorrer el arco de la circunferencia AB será el mismo que el tiempo TAB que tarda el cometa en recorrer el arco de elipse AB
Orbita circular del planeta
Dinámica del movimiento circular
El tiempo que emplea el planeta en desplazarse desde A hasta B es
Trayectoria elíptica
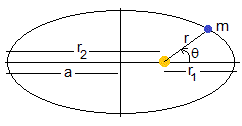
El perigeo θ=0, r1=d/(1+ε), el apogeo θ=π, r2=d/(1-ε), r1+r2=2a
La posición angular φ de los puntos de intersección A y B de las órbitas circular y elíptica son
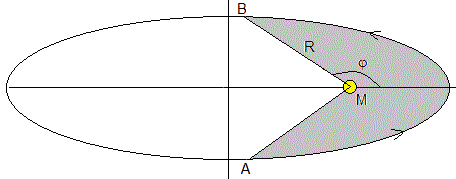
Integrando la ecuación del momento angular expresado en coordenadas polares calculamos el tiempo TAB que emplea el cometa en desplazarse desde A hasta B
El primer miembro es el área barrida por el radio vector cuando el cometa se desplaza de A a B, sombreada de color gris claro
Calculamos la mitad de área A/2 (en color gris claro)
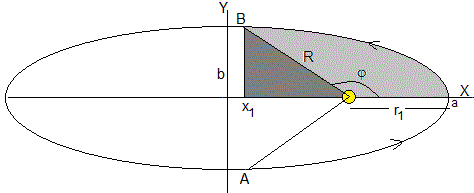
Hacemos el cambio de variable, x=a·sinz, dx=a·cosz·dz
El área A barrida por el radio vector es
El tiempo TAB es
Los tiempos tAB= TAB son iguales si
Dada la excentricidad ε de la órbita elíptica, obtenemos la raíz R/a de la ecuación transcendente
Sea un cometa de excentricidad ε=0.967, y semieje mayor a= 17.834 UA (unidades astronómicas, 1 UA=1.496·108 km)
ex=0.967; %excentricidad
f=@(x) acos((1-(1-ex^2)/x)/ex)*x^(3/2)-pi/2+asin((1-x)/ex)+((1-x)/ex)*
sqrt(1-((1-x)/ex)^2)-(x^2)*((1-ex^2)/x-1)*sqrt(1-(((1-ex^2)/x-1)/ex)^2)
/(ex*sqrt(1-ex^2));
xi=fzero(f,0.3); %raíz R/a
a=17.834;
R=xi*a;
hold on
fplot(@(t) R*cos(t),@(t) R*sin(t),[0,2*pi]) %órbita circular
r=@(t) a*(1-ex^2)./(1+ex*cos(t)); %órbita elíptica
fplot(@(t) r(t).*cos(t), @(t) r(t).*sin(t),[0,2*pi])
xx=0.5*cos((0:180)/pi);
yy=0.5*sin((0:180)/pi);
fill(xx,yy,'r') %sol
hold off
grid on
xlabel('x')
ylabel('y')
axis equal
title('dos encuentros')
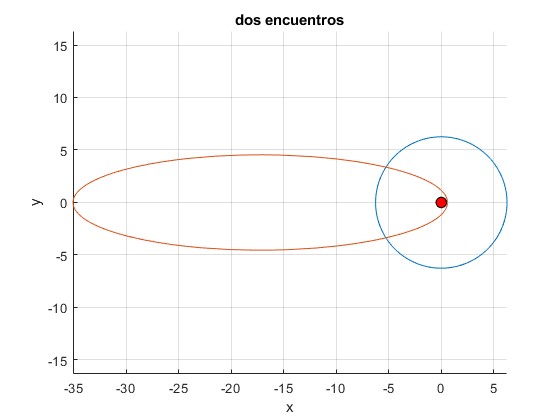
La raíz R/a de la ecuación transcendente es
>> xi xi = 0.3509
Referencias
O. L. de Lange, J. Pierrus. Solved Problems in Classical Mechanics. Analytical and numerical solutions with comments. Oxford University Press (2010). Question 8.20, pp. 260-262
2020 Online Physics Olympiad: Open Contest. pp. 48-49. Problem 51
B Cameron Reed. Close encounters of the cometary kind. Eur. J. Phys. 46 (2025) 065007

