Solución numérica de las ecuaciones del movimiento

Las leyes de Kepler describen el movimiento de los planetas en torno del Sol, sin indagar en las causas que producen tal movimiento.

1.-Los planetas describen órbitas elípticas estando el Sol en uno de sus focos.

2.-El vector posición de cualquier planeta con respecto del Sol, barre áreas iguales de la elipse en tiempos iguales.

3.-Los cuadrados de los periodos de revolución son proporcionales a los cubos de los semiejes de la elipse.

Las leyes de Newton, no solamente explican las leyes de Kepler sino que predicen otras trayectorias para los cuerpos celestes: las parábolas y las hipérbolas. En general, un cuerpo bajo la acción de la fuerza de atracción gravitatoria describirá una trayectoria plana que es una cónica.

Como se ha comentado, las propiedades central y conservativa de la fuerza de atracción entre un cuerpo celeste y el Sol, determinan un sistema de dos ecuaciones diferenciales de primer orden, que cuando se expresan en coordenadas polares, conducen a la ecuación de la trayectoria, una cónica.

En esta página, se procede de otro modo: se calculan las componentes de la aceleración a lo largo del eje X y a lo largo del eje Y, dando lugar a un sistema de dos ecuaciones diferenciales de segundo orden que se resuelven por procedimientos numéricos

Solución numérica de las ecuaciones del movimiento

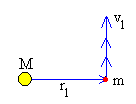
Supongamos que una partícula de masa m (un planeta) es atraída por un cuerpo masivo de masa M (el Sol) Supondremos que la la influencia de la partícula sobre el cuerpo es despreciable permaneciendo en reposo en el origen.

La partícula está sometida a una fuerza atractiva cuya dirección es radial y apuntando hacia el centro del Sol. El módulo de la fuerza viene dado por la ley de la Gravitación Universal

$F = G \frac{M m}{r^{2}}$

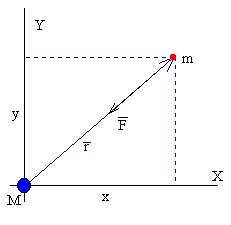
Siendo r la distancia entre la partícula y el centro de fuerzas, y x e y su posición respecto del sistema de referencia cuyo origen está situado en el Sol. $r = \sqrt{x^{2} + y^{2}}$

Las componentes de la fuerza son

$\begin{array}{l} F_{x} = - F \cos θ = - F \frac{x}{r} \\ F_{y} = - F \sin θ = - F \frac{y}{r} \end{array}$

Aplicando la segunda ley de Newton, y expresando la aceleración como derivada segunda de la posición, tenemos un sistema de dos ecuaciones diferenciales de segundo orden.

$\begin{array}{l} m \frac{d^{2} x}{d t^{2}} = - G \frac{m M}{r^{2}} \frac{x}{r} \\ m \frac{d^{2} y}{d t^{2}} = - G \frac{m M}{r^{2}} \frac{y}{r} \end{array}$

Dadas las condiciones iniciales (posición y velocidad inicial), el sistema de dos ecuaciones diferenciales se puede resolver aplicando un procedimiento numérico como el de Runge-Kutta.

Escalas

Antes de resolver el sistema de ecuaciones diferenciales por procedimientos numéricos, es conveniente prepararlas para que el ordenador no maneje números excesivamente grandes o pequeños.

Establecemos un sistema de unidades en el que la longitud se mide en unidades r₀=1.496·10¹¹ m y el tiempo en unidades P=2πr₀/v₀, el tiempo que tarda en dar una vuelta completa. La ecuación de la dinámica del movimiento circular uniforme

$G \frac{M m}{r_{0}^{2}} = m \frac{v_{0}^{2}}{r_{0}}, v_{0} = \sqrt{\frac{G M}{r_{0}}}$

El sistema de ecuaciones diferenciales se transforma en

$\begin{array}{l} \frac{d^{2} x}{d t^{2}} = - G \frac{M}{r^{2}} \frac{x}{r} \\ \frac{d^{2} X}{d τ^{2}} \frac{r_{0}}{P^{2}} = - G M \frac{X}{{(X^{2} + Y^{2})}^{3 / 2}} \frac{1}{r_{0}^{2}} \\ \frac{d^{2} X}{d τ^{2}} = - 4 π^{2} \frac{X}{{(X^{2} + Y^{2})}^{3 / 2}} \end{array}$

Lo mismo para la ecuación diferencial en y.

$\frac{d^{2} Y}{d τ^{2}} = - 4 π^{2} \frac{Y}{{(X^{2} + Y^{2})}^{3 / 2}}$

Volviendo a la notación x e y para la posición y t para el tiempo en el nuevo sistema de unidades. El sistema de ecuaciones diferenciales se escribe

$\begin{array}{l} \frac{d^{2} x}{d t^{2}} = - 4 π^{2} \frac{x}{{(x^{2} + y^{2})}^{3 / 2}} \\ \frac{d^{2} y}{d t^{2}} = - 4 π^{2} \frac{y}{{(x^{2} + y^{2})}^{3 / 2}} \end{array}$

Se resuelve por procedimientos numéricos con las condiciones iniciales siguientes: en el instante t=0, x=x₀, y=0, v_x=0, v_y=v_0y.

Principio de conservación de la energía

La energía total de la partícula es una constante del movimiento. La energía de la partícula de masa m en el instante inicial t=0 es

$E_{0} = \frac{1}{2} m v_{0}^{2} - \frac{G m M}{r_{0}}$

Cuando E₀<0 la partícula permanece confinada en el espacio que rodea a los dos cuerpos. Cuando E₀≥0 la partícula escapa al infinito

La energía de la partícula en el instante t es igual a

$E = \frac{1}{2} m (v_{x}^{2} + v_{y}^{2}) - \frac{G m M}{\sqrt{x^{2} + y^{2}}}$

En el nuevo sistema de unidades establecido

$\begin{array}{l} \frac{E}{m} = \frac{1}{2} V^{2} \frac{r_{0}^{2}}{P^{2}} - \frac{G M}{r_{0}} \frac{1}{\sqrt{X^{2} + Y^{2}}} \\ \frac{E}{m} = \frac{v_{0}^{2}}{4 π^{2}} (\frac{1}{2} V^{2} - 4 π^{2} \frac{1}{\sqrt{X^{2} + Y^{2}}}) \end{array}$

Volviendo a la notación previa. Definimos una nueva energía e por unidad de masa en este sistema de unidades

$e = \frac{1}{2} (v_{x}^{2} + v_{y}^{2}) - 4 π^{2} \frac{1}{\sqrt{x^{2} + y^{2}}}$

El programa interactivo evalúa en cada instante el cociente

$| \frac{e - e_{0}}{e_{0}} | \cdot 100$

que denominaremos tanto por ciento de error. Cuando la energía e difiere de e₀ de modo que el cociente es mayor que la unidad el programa interactivo se detiene, la trayectoria calculada puede que se desvíe significativamente de la real y esto suele ocurrir cuando la partícula está muy cerca del centro de fuerzas

Ejemplo: Marte

Los datos de Marte son:

Semieje mayor a=1.524 UA,
Excentricidad ε=0.093.

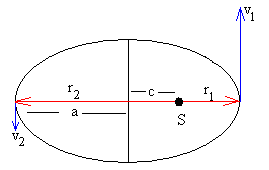
La distancia más cercana al Sol (perihelio) es r₁=a-c=a-εa=1.382 UA=2.068·10¹¹ m

La distancia más alejada del Sol (afelio) es r₂=a+c=a+εa=1.666 UA=2.492·10¹¹ m

Conocidas las distancias máxima y mínima r₁ y r₂ calculamos la velocidad en el perihelio v₁

$v_{1} = \sqrt{\frac{2 G M r_{2}}{r_{1} (r_{1} + r_{2})}}$

v₁=26420.7 m/s=5.573 UA/año

Cuando introducimos en el programa interactivo x=1.382 y v_y=5.573, obtenemos la trayectoria elíptica de Marte alrededor del Sol y el tiempo que tarda en dar una vuelta completa P=1.86 años.

Actividades

En el programa interactivo, más abajo, se trazarán las trayectorias que describen los cuerpos celestes. Se comprobará la constancia de la energía, se verificará que el momento angular es constante en las posiciones de máxima proximidad o de máximo alejamiento y por último, se comprobará la tercera ley de Kepler, midiendo el periodo y el semieje mayor de la elipse. Se introducen la posición y la velocidad inicial del cuerpo celeste:

La posición inicial x, la ordenada y=0, en el control titulado Posición X
La componente Y de la velocidad inicial v_y, la componente X de la velocidad v_x =0, en el control titulado Velocidad V_y

Se pulsa el botón titulado Nuevo y a continuación ►, se traza la trayectoria del móvil, al mismo tiempo se muestra en la parte izquierda, como van cambiando los valores de la posición y de la velocidad a medida que transcurre el tiempo.

Observaremos que la energía y el momento angular permanecen constantes. En la parte inferior izquierda, se muestra en color azul el tanto por ciento de error. Cuando es mayor que la unidad el programa interactivo se detiene. Los mayores porcentajes de error se obtienen cuando la partícula pasa muy cerca del centro fijo de fuerzas.

Se pulsa el botón titulado pausa || y luego, paso a paso >|, para acercarnos a la posición más alejada, para medir el semieje mayor, la velocidad en dicha posición, el semiperiodo (la mitad del tiempo que tarda el cuerpo celeste en dar una vuelta completa).

Se introduce la velocidad inicial en UA/año de un nuevo cuerpo sin cambiar la posición y se pulsa los botoness Nuevo y ►. Su trayectoria se traza en un color distinto.

Finalmente, se cambia la posición inicial x y se vuelven a introducir varios valores de la velocidad v_y. Cuando se han acumulado varias trayectorias, se pulsa en el botón Borra para limpiar el área de trabajo

Posición X
Velocidad V_y

La órbita de la Tierra

Conocidos el semieje mayor de la elipse a y la excentricidad ε, calculamos la posición del planeta en el perihelio r₁ (posición más cercana al Sol) o r₂ en el afelio (posición más alejada), tal como hemos visto al estudiar la órbita elíptica.

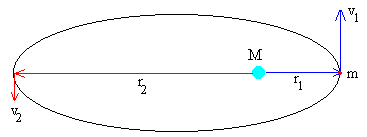
Calculamos la velocidad v₁ en el perihelio o v₂ en el afelio a partir de las propiedades de la fuerza de atracción entre los cuerpos:

Es una fuera central por lo que el momento angular $\vec{L}$ permanece constante. La trayectoria de la partícula está contenida en un plano (la eclíptica) perpendicular a la dirección del momento angular.
Es una fuerza conservativa. La energía total E (suma de cinética más potencial) permanece constante

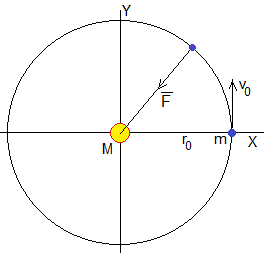
En la figura, se muestra un cuerpo que describe una trayectoria elíptica alrededor del centro de fuerzas situado en uno de sus focos. La distancia de máximo acercamiento es r₁ y la de máximo alejamiento r₂. Las velocidades que lleva el cuerpo en estas dos posiciones extremas son v₁ y v₂ respectivamente. La constancia del momento angular y de la energía nos permite relacionar estas cuatro magnitudes.

$\begin{array}{l} m r_{1} v_{1} = m r_{2} v_{2} \\ \frac{1}{2} m v_{1}^{2} - \frac{G m M}{r_{1}} = \frac{1}{2} m v_{2}^{2} - \frac{G m M}{r_{2}} \end{array}$

Conocidos r₁ y r₂ calculamos v₁ y v₂.

Se despeja v₁ en la primera ecuación y se sustituye en la segunda. Obtenemos

$v_{2} = \sqrt{\frac{2 G M r_{1}}{r_{2} (r_{1} + r_{2})}} v_{1} = \sqrt{\frac{2 G M r_{2}}{r_{1} (r_{1} + r_{2})}}$

Calculamos r₁ y v₁ para la Tierra que tiene un semieje mayor a=1.0 UA y una excentricidad ε=0.017. Estos son los valores iniciales para resolver el sistema de dos ecuaciones diferenciales de segundo orden utilizando la función ode45 de MATLAB e interrumpiendo el proceso de cálculo cuando se complete un periodo.

$\begin{array}{l} r_{1} = \frac{d}{1 + ε} r_{2} = \frac{d}{1 - ε} \\ r_{1} + r_{2} = 2 a \\ r_{1} = a (1 - ε) \\ v_{1} = \sqrt{\frac{2 G M r_{2}}{r_{1} (r_{1} + r_{2})}} = \sqrt{\frac{2 G M a (1 + ε)}{a (1 - ε) \cdot 2 a}} = \frac{2 π a}{P} \sqrt{\frac{1 + ε}{1 - ε}} \end{array}$

En el sistema de unidades que hemos adoptado a= 1 U.A. y P=1 (un año)

Creamos el script para realizar las siguientes tareas:

Resolvemos mediante ode45 el sistema de dos ecuaciones diferenciales de segundo orden con las condiciones iniciales

Posición inicial (x₀, y₀): x0(1)=r₁, x0(3)=0
Velocidad inicial (v_x0, v_y0): x0(2)=0, x0(4)=v₁

Definimos la función stop_tierra que detiene el proceso de integración, fijándonos que en el pimer semiperiodo la ordenda y decrece hasta hacerse cero y a continuación, la ordenada y crece hasta hacerse de nuevo cero cuando completa el periodo. Obtenemos el tiempo de una órbita completa te
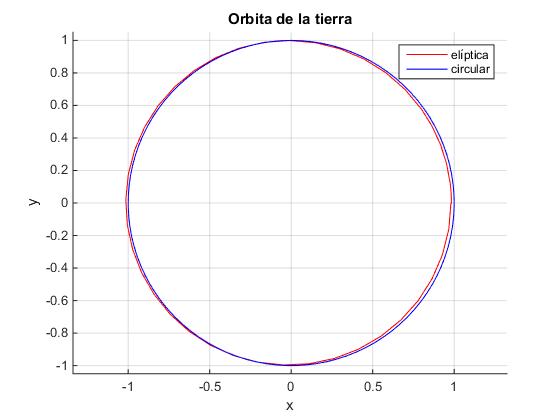
Dibujamos la órbita elíptica en color rojo y una trayectoria circular de radio a=1 UA en color azul
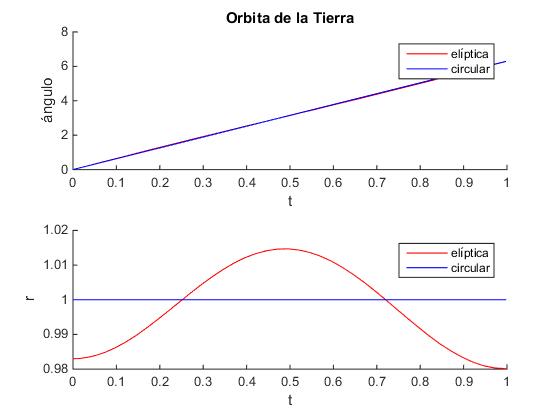
Dibujamos en una segunda ventana la posición angular θ en función del tiempo t, utilizando la función MATLAB atan2. Fijarse que atan2 devuelve el ángulo en el intervalo -π a +π, en vez de 0 a 2π. Comparamos esta gráfica con la correspondiente a un movimiento circular uniforme durante un tiempo igual a un periodo te. Dibujamos en la misma ventana (utilizando el comando subplot) la distancia r de la Tierra al Sol en función del tiempo t. La comparamos con la distancia constante al centro a=1 de la órbita circular.

a=1; ex=0.017; P=1;
x0=[a*(1-ex),0,0,2*pi*a*sqrt((1+ex)/(1-ex))/P];
tspan=[0,P];

fg=@(t,x)[x(2);-4*pi^2*x(1)/(sqrt(x(1)*x(1)+x(3)*x(3)))^3; x(4);
-4*pi^2*x(3)/(sqrt(x(1)*x(1)+x(3)*x(3)))^3];
opts=odeset('events',@stop_tierra);
[t,x,te,xe,ie]=ode45(fg,tspan,x0,opts);
te
hold on
plot(x(:,1),x(:,3),'r') %órbita elíptica
ang=linspace(0,2*pi,100); %órbita circular
xx=sin(ang); yy=cos(ang);
plot(xx,yy,'b')
axis equal
ylim([-1.05 1.05])
legend('elíptica', 'circular','location','best')
grid on
xlabel('x')
ylabel('y');
title('órbita de la tierra')
hold off

figure
subplot(2,1,1)
angulo=atan2(x(:,3),x(:,1));
for i=1:length(angulo)
    if angulo(i)<0
        angulo(i)=angulo(i)+2*pi;
    end
end
angulo(length(t))=2*pi+angulo(length(t));
hold on
plot(t,angulo,'r')
angulo_c=(2*pi/te(2))*t;
plot(t,angulo_c,'b')
xlabel('t')
ylabel('angulo');
title('órbita de la Tierra')
legend('elíptica', 'circular','location','best')
hold off

subplot(2,1,2)
r=sqrt(x(:,1).^2+x(:,3).^2);
hold on
plot(t,r,'r')
plot([0,te(2)],[1 1],'b')
xlabel('t')
ylabel('r');
legend('elíptica', 'circular',2)
hold off

Definimos una función denominada stop_tierra para parar el proceso de integración cuando complete un periodo, es decir, cuando la ordenada y que en el código es x(3) sea cero (stopin=1) y sea una función creciente (direction=1).

function [detect,stopin,direction]=stop_tierra(t,x)
    detect=x(3); 
    stopin=1; 
    direction=1; 
end

En la la ventana de comandos corremos el script tierra.

>> tierra
te =
    0.0000
    0.9969

El proceso de integración numérica se detiene cuando el tiempo te es 0.9969 años, muy próximo a P= 1 año.

Debido a la pequeña excentricidad de la Tierra ε=0.017 no se aprecia gran diferencia entre la órbita elíptica y circular y tampoco, en la gráfica de la posición angular en función del tiempo.