El observador no está situado en la dirección del movimiento rectilíneo del emisor

En una página anterior, hemos estudiado el caso de un emisor que se mueve a lo largo de una recta con velocidad constante v_E y el observador está situado en un punto de dicha recta.

Consideremos una situación algo más compleja. Supongamos que el observador está a una distancia R de la dirección en la que se mueve el emisor, tal como se indica en la figura.

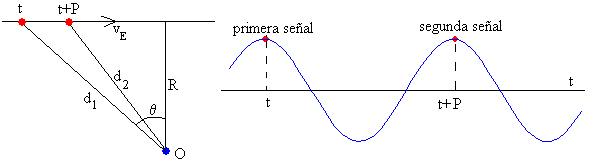
• En el instante t el emisor emite la primera señal que puede corresponder a un máximo de una onda armónica. El observador la escucha en el instante t₁. Si en el instante t la distancia entre el emisor y el observador es d₁, tendremos

t₁=t+d₁/v_s

siendo v_s la velocidad del sonido.

• En el instante t+P se emite la segunda señal. El observador la escucha en el instante t₂. Si en el instante t+P la distancia entre el emisor y el observador es d₂, tendremos que

t₂=t+P+d₂/v_s

siendo P el periodo de la onda armónica

Para el observador, el periodo P’ de la onda armónica será la diferencia de los tiempos de llegada de las dos señales

${\displaystyle P\text{'}=t_2-t_1=P+\frac{d_2-d_1}{v_s}}$

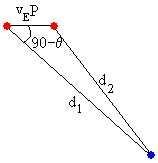
La relación entre d₂ y d₁ se puede deducir resolviendo el triángulo de la figura

${\displaystyle \begin{array}{l}{d}_2^2=d_1^2+{\left(v_{E}P\right)}^2-2d_1{v}_{E}P\text{cos(90-}\theta )\\ d_2^2=d_1^2\left(1+{\left(\frac{v_{E}P}{d_1}\right)}^2-2\frac{v_{E}P}{d_1}\sin \theta \right)\end{array}}$

Obtenemos una expresión más simplificada, si consideramos la siguiente aproximación, el lado de longitud v_E·P es mucho menor que cualquiera de los otros dos lados de longitud d₁ o d₂.

Despreciamos el cociente al cuadrado frente a la unidad y efectuamos el desarrollo en serie

${\displaystyle {(1-x)}^{1/2}=1-\frac{1}{2}x+\mathrm{...}x<<1}$

tenemos que

${\displaystyle d_2\approx d_1\sqrt{1-2\frac{v_{E}P}{d_1}\sin \theta }\approx d_1\left(1-\frac{v_{E}P}{d_1}\sin \theta \right)=d_1-v_{E}P\sin \theta }$

El periodo P’ de la onda armónica medido por el observador, valdrá

${\displaystyle P\text{'}=P+\frac{d_2-d_1}{v_s}\approx P-\frac{v_E}{v_s}P\sin \theta }$

La frecuencia es la inversa del periodo f’=1/P’

${\displaystyle f\text{'}=f\frac{v_s}{v_s-v_E\sin \theta }}$

Fórmula aproximada

Esta fórmula se puede obtener de forma directa si partimos de la fórmula del efecto Doppler para el caso más simple: el observador en reposo v_O=0 situado en la trayectoria del emisor en movimiento rectilíneo con velocidad v_E constante.

${\displaystyle f\text{'}=f\frac{v_s}{v_s-v_E}}$

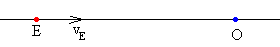
Cuando el observador no está en la dirección del movimiento rectilíneo del emisor, trazamos una línea recta que pase por el emisor y el observador en el instante t, proyectamos la velocidad v_E del emisor a lo largo de dicha recta.

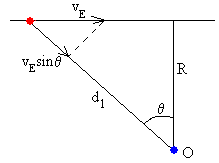
En dicho instante, el emisor se acerca al observador con una velocidad v_E·sinθ, tal como puede apreciarse en la figura. Sustituimos v_E por v_E·sinθ y obtenemos la misma fórmula.

${\displaystyle f\text{'}=f\frac{v_s}{v_s-v_E\sin \theta }}$

El emisor describe un movimiento circular

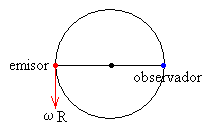
Supongamos ahora que el emisor describe una trayectoria circular de radio R con velocidad angular ω constante. El observador en reposo está situado a una distancia R del centro de la trayectoria circular, en el origen de ángulos, tal como se muestra en la figura.

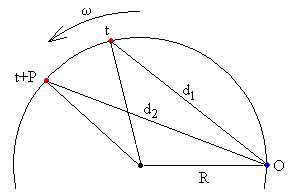
• En el instante t el emisor emite la primera señal que puede corresponder a un máximo de una onda armónica. El observador la escucha en el instante t₁. Si en el instante t la distancia entre el emisor y el observador es d₁, tendremos
  t₁=t+d₁/v_s
   

• En el instante t+P se emite la segunda señal. El observador la escucha en el instante t₂. Si en el instante t+P la distancia entre el emisor y el observador es d₂, tendremos que
  t₂=t+P+d₂/v_s

El periodo del movimiento ondulatorio armónico medido por el observador es P’=t₂-t₁=P+(d₂-d₁)/v_s

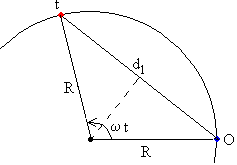
En el triángulo isósceles de la figura, se puede calcular fácilmente, d₁ conocido el radio R y el ángulo ωt.

d₁=2R·sin(ωt/2)

De modo similar se calcula d₂.

${\displaystyle \begin{array}{l}P\text{'}=P+\frac{d_2-d_1}{v_s}=P+\frac{2R}{v_s}\left(\sin \left(\frac{\omega (t+P)}{2}\right)-\sin \left(\frac{\omega t}{2}\right)\right)=\\ P+\frac{4R}{v_s}\sin \left(\frac{\omega P}{4}\right)\cos \left(\frac{\omega t}{2}+\frac{\omega P}{4}\right)\end{array}}$

Esta fórmula se puede simplificar, si consideramos que ωP es pequeño y por tanto, podamos escribir sin(x)≈x.

${\displaystyle P\text{'}\approx P+\frac{4R}{v_s}\left(\frac{\omega P}{4}\right)\cos \left(\frac{\omega t}{2}\right)=\frac{P}{v_s}\left(v_s+\omega R\cos \left(\frac{\omega t}{2}\right)\right)}$

La frecuencia es la inversa del periodo f’=1/P’

${\displaystyle f\text{'}=f\frac{v_s}{v_s+\omega R\cos \left(\frac{\omega t}{2}\right)}}$

Fórmula aproximada

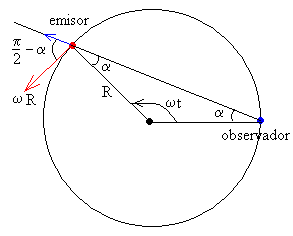
El emisor describe una trayectoria circular de radio R, con velocidad angular ω constante, su posición angular en el instante t es ωt, y su velocidad es ωR, tangente a la trayectoria, tal como se muestra en la figura.

La velocidad v_E es la proyección de la velocidad del emisor sobre la recta que une el emisor y el observador (flecha azul)

En el triángulo isósceles formado por los dos radios y la línea que une el emisor y el observador, el ángulo α vale α=π/2-ωt/2.

Como v_E=ωR·cos(π/2-α)= ωR·cos(ωt/2)

La fórmula que describe el efecto Doppler que se produce en esta situación es

${\displaystyle f\text{'}=f\frac{v_s}{v_s+\omega R\cos \left(\frac{\omega t}{2}\right)}}$

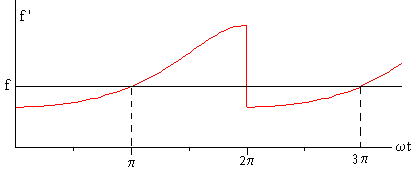
• Cuando ωt<π el emisor se aleja del observador f '<f

• Cuando ωt>π el emisor se acerca del observador f '>f

• Cuando ωt=π la línea que une el emisor y el observador es el diámetro horizontal y la proyección de la velocidad del emisor sobre el diámetro es cero. La frecuencia del sonido que escucha el observador es la misma que la que emite la fuente de sonido f'=f

Cuando ωt=2π se produce una discontinuidad. La frecuencia f’ pasa de un máximo (el emisor se acerca al observador)

${\displaystyle f\text{'}=f\frac{v_s}{v_s-\omega R}}$

a un mínimo, (el emisor se aleja del observador)

${\displaystyle f\text{'}=f\frac{v_s}{v_s+\omega R}}$

En la figura, se representa la frecuencia f’ en función de ωt.

Vamos a comparar la fórmula exacta y la aproximada

Supongamos como en la simulación que v_s=1, R=1, Calculamos la frecuencia f' del sonido que escucha el observador suponiendo que el que emite la fuente tiene una frecuencia f=4.

1. La primera columna es la velocidad ωR del emisor, inferior a la velocidad del sonido v_s=1
2. La segunda columna, calcula la mínima frecuencia, cuando el emisor situado en la posición del observador ωt=0, se aleja.
3. La tercera columna, calcula la frecuencia intermedia, cuando el emisor no se aleja ni se acerca al observador ωt=π.
4. La cuarta columna, calcula la máxima frecuencia, cuando el emisor situado en la posición del observador ωt=2π, se acerca.

• La columnas de la izquierda corresponden a las frecuencias f’ calculadas mediante la fórmula aproximada
• La columnas de la derecha corresponden a las frecuencias f’ calculadas mediante la fórmula exacta.

Observamos que apenas hay diferencias en los valores calculados de la frecuencia f’ por ambas fórmulas.

Estas diferencias se hacen cada vez más pronunciadas cuando la frecuencia f es más pequeña, la velocidad de rotación ω es más grande y el emisor se aleja del observador (máxima frecuencia).

Actividades

Se introduce

• La velocidad angular de rotación ω, un número comprendido entre 0 y 1, en el control titulado Velocidad emisor
• El radio de la circunferencia que describe la fuente de sonido se ha fijado en la unidad, R=1.
• La velocidad del sonido se ha fijado en la unidad, v_s=1
• La frecuencia del sonido que emite la fuente se ha fijado en f=4, o el periodo en P=1/f=0.25 unidades de tiempo.

Se pulsa el botón titulado Nuevo.

Se observa el movimiento de la fuente de sonido representada por un pequeño círculo de color rojo, que describe una trayectoria circular con velocidad angular constante. El micrófono está representado por un pequeño círculo de color azul inmóvil.

La fuente de sonido describe un MAS de la forma Ψ=Ψ₀·cos(8πt), emitiendo ondas circulares cuyos máximos se representan por circunferencias de color rojo.

La intersección del movimiento ondulatorio armónico con la línea que une el emisor y el observador se representa en la parte inferior.

Esta representación nos permite relacionar la velocidad v_E (proyección de la velocidad de la fuente ωR a lo largo de la línea que une el emisor y el observador), con la frecuencia f’ del sonido que escucha el observador. Se representa mediante vectores la velocidad de la fuente (color negro) y su proyección (color rojo).

La señal de frecuencia f’ producida en la posición que ocupa el emisor tarda un determinado tiempo en llegar al observador, igual a la distancia emisor-observador dividido por la velocidad del sonido.

En la parte derecha, se representa la frecuencia f’ en función de ωt, posición angular de la fuente emisora.

• Cuando ωt=(2k+1)π, k=0, 1, 2, 3… la frecuencia f’=f=4.

• Cuando ωt=2kπ, k=0, 1, 2, 3…la frecuencia f’ pasa de un máximo a un mínimo.

Ejemplo:

Si introducimos ω=0.5

• La máxima frecuencia del sonido que escucha el observador es

${\displaystyle f\text{'}=\frac{4}{1-0.5·1}=8}$

• La mínima frecuencia que escucha es

${\displaystyle f\text{'}=\frac{4}{1+0.5·1}=\frac{8}{3}}$

El emisor describe un movimiento circular, el observador está a una distancia de su centro

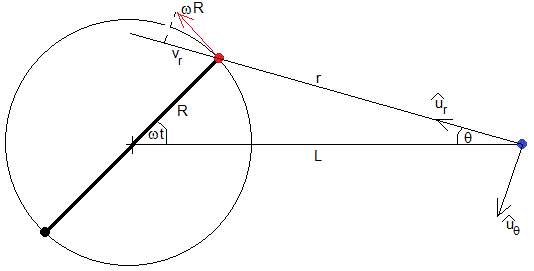
Supongamos que un altavoz (en color rojo) está sujeto en el extremo de una barra de longitud 2R que gira con velocidad angular constante ω, en el otro extremo se coloca un contrapeso. Un micrófono (en color azul) está situado a una distancia L del eje de giro.

Cuando la distancia L=R repetimos la experiencia descrita en el apartado anterior

El efecto Doppler depende de la componente de la velocidad v_r que es paralela a la línea que une la fuente y el detector.

${\displaystyle f\text{'}=f\frac{v_s}{v_s+v_r}}$

En el caso de que v_r<<v_s,

${\displaystyle f\text{'}=f{\left(1+\frac{v_r}{v_s}\right)}^{-1}\approx f\left(1-\frac{v_r}{v_s}\right)}$

Si la fuente se aleja del micrófono v_r>0, f'<f, en el intervalo de tiempo (0<t<π/ω) mientras que si la fuente se acerca al micrófono, v_r<0, f'>f, en el intervalo de tiempo (π/ω<t<2π/ω). En los instantes t=π/ω y t=2π/ω, el vector velocidad es perpendicular a la línea que une la fuente y el micrófono, v_r=0, y las frecuencias f' y f coinciden.

El módulo de la velocidad del emisor v=ωR y su dirección tangente a la circunferencia de radio R (flecha de color rojo)

Considerando el micrófono como el origen de un sistema de referencia en coordenadas polares. El vector velocidad se expresa

${\displaystyle \overrightarrow{v}=\frac{dr}{dt}\widehat{r}+r\frac{dr}{dt}\widehat{\theta }}$

La componente radial de la velocidad es v_r=dr/dt. La distancia r entre la fuente y el micrófono es

${\displaystyle r^2=L^2+R^2-2LR\cos (\omega t)}$

Derivando con respecto al tiempo

${\displaystyle \begin{array}{l}2r\frac{dr}{dt}=2LR\omega \sin (\omega t)\\ v_r=\frac{LR\omega \sin (\omega t)}{\sqrt{L^2+R^2-2LR\cos (\omega t)}}\end{array}}$

La frecuencia del sonido medido por el observador es

${\displaystyle f\text{'}=f\frac{v_s}{v_s+\frac{LR\omega \sin (\omega t)}{\sqrt{L^2+R^2-2LR\cos (\omega t)}}}}$

Ejemplo

• Velocidad angular de rotación, ω=42 rad/s
• Distancia del eje de giro al micrófono, L=53 cm
• Radio de la circunferencia que describe el emisor, R=26.5 cm
• Velocidad del sonido, v_s=349 m/s
• Frecuencia del sonido emitido, cuando el altavoz está en reposo, f=15 kHz

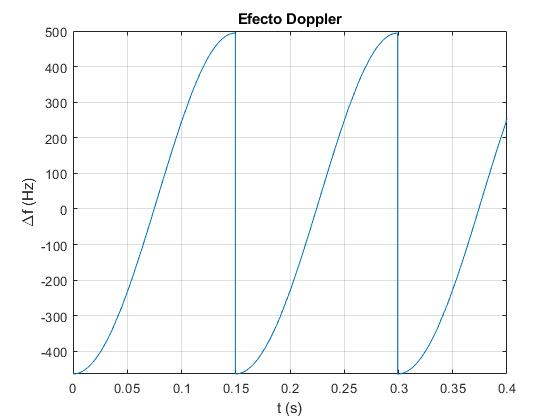
Representamos la diferencia Δf=f'-f, desviación debido al efecto Doppler, en función del tiempo t

w=42; %velocidad angular de rotación
R=0.265; %radio de la circunferencia que describe
L=0.53; %distancia del eje de giro al micrófono
vs=349; %velocidad del sonido
f=15000; %frecuencia que emite la fuente

fp=@(t) f*vs./(vs+L*R*w*sin(w*t)./sqrt(L^2+R^2-2*L*R*cos(w*t)))-f;
%fp=@(t) f*(1-w*R*sin(w*t)./(vs*sqrt(1+(R/L)^2-2*R*cos(w*t)/L)))-f; %aproximación
fplot(fp,[0,0.4])
grid on
xlabel('t (s)')
ylabel('\Deltaf (Hz)')
title('Efecto Doppler')

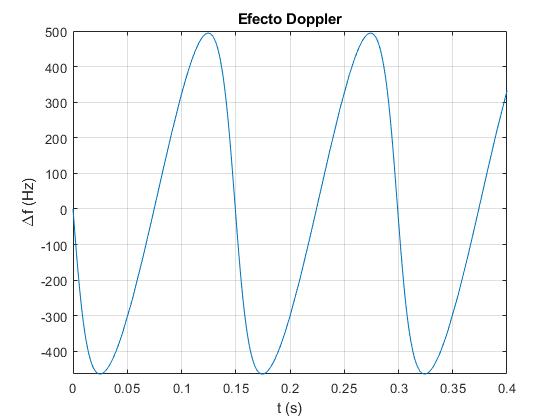
La fórmula exacta y la aproximación v_r<<v_s producen los mismos resultados

No hay desviación f'-f=0 en los instantes π/ω+nP y nP, donde P=2π/ω=0.15 s es el periodo y n=1,2,3... es un número entero

Cuando L=R reproducimos los resultados del apartado anterior

Referencias

Saba M., Rosa R A., The Doppler effect of a sound source moving in a circle. The Physics Teacher, Vol 41, February 2003, pp. 89-91.

Kader Médjahdi. Radial velocity of a sound source in circular motion for illustrating the detection of an exoplanet. Am. J. Phys. 88 (10), October 2020, pp. 814-818