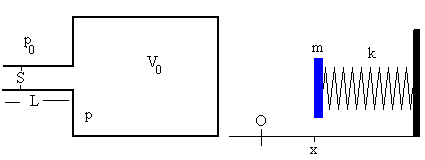
Un resonador ideal consiste en una cavidad de volumen V con un cuello de área S y de longitud L. Si la longitud de onda λ es mucho más grande que sus dimensiones L, S^1/2 y V^1/3, el aire del cuello se mueve como un bloque de masa m.

El aire contenido en el gran volumen V₀ actúa como un muelle de constante elástica k que está unido a un bloque de masa m que es el aire del cuello de la botella.

La deducción de la frecuencia de oscilación es similar a la empleada para calcular la frecuencia de las oscilaciones de una esfera en el experimento de la medida del índice adiabático de un gas ideal.

Transformación adiabática

Si suponemos que la oscilación transcurre muy rápidamente, los cambios de presión y de volumen del gas del recipiente, se describen mediante un proceso adiabático. La relación entre la presión y el volumen del gas para dicho proceso viene dada por la ecuación.

${\displaystyle p{V}^{\gamma }=\text{cte}}$

donde V es el volumen del gas, p la presión y γ el índice adiabático del gas.

Cuando la porción de aire en el cuello de la botella, se ha desplazado x de la posición de equilibrio, el volumen se ha reducido en V₀-Sx y la presión a cambiado a p de modo que

${\displaystyle p_0{V}_0^{\gamma }=p{\left(V_0-S·x\right)}^{\gamma }}$

Despejando p

${\displaystyle p=p_0{\left(1-\frac{S·x}{V_0}\right)}^{-\gamma }}$

Dado que S·x<< V₀. El desarrollo del binomio de Newton (a+b)ⁿ hasta el primer término, nos da la presión aproximada p.

${\displaystyle p\approx p_0\left(1+\gamma \frac{S}{V_0}x\right)}$

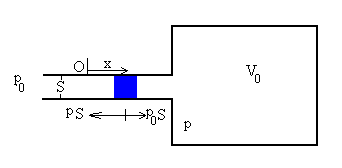
La fuerza neta que actúa sobre dicha porción de aire de masa m será

${\displaystyle F=\left(p_0-p\right)S=-p_0\gamma \frac{S^2}{V_0}x}$

La fuerza F es proporcional al desplazamiento x  y de sentido contrario a éste, un claro signo de que la porción de aire describe un M.A.S.

Cuando la masa m de aire (en color azul) se desplaza hacia la derecha, la presión aumenta, la fuerza sobre la partícula está dirigida hacia la izquierda. Cuando la masa m se desplaza hacia la izquierda la presión disminuye, la fuerza sobre la partícula es hacia la derecha. Por tanto, la fuerza sobre la partícula es de sentido contrario al desplazamiento, una de las características del M.A.S.

Oscilaciones armónicas

La segunda ley de Newton se escribe

${\displaystyle m\frac{d^{2}x}{d{t}^2}+p_0\gamma \frac{S^2}{V_0}x=0}$

Ecuación diferencial de un Movimiento Armónico Simple (M.A.S.) de frecuencia

${\displaystyle {\omega }_0^2=\frac{\gamma S^2{p}_0}{m{V}_0}}$

Teniendo en cuenta que la fórmula de la velocidad del sonido en un gas de presión p₀ y densidad ρ₀ es

${\displaystyle v_s=\sqrt{\frac{\gamma p_0}{{\rho }_0}}}$

y que la partícula de masa m es aquí el aire contenido en el cuello de la botella

m=ρ₀·SL

Obtenemos la expresión de la frecuencia angular ω₀ de las oscilaciones de dicha masa de aire

${\displaystyle {\omega }_0=v_s\sqrt{\frac{S}{L{V}_0}}}$

La fórmula aplicable experimentalmente es

${\displaystyle {\omega }_0=v_s\sqrt{\frac{S}{L_e{V}_0}}}$

Donde L_e=L+ΔL es la longitud efectiva del cuello. La longitud efectiva L_e es la longitud real L del cuello más alrededor de 0.7 de radio del cuello r a cada lado, es decir, L_e=L+1.4·r, este factor puede variar de 1.3 a 1.7.

Determinación del volumen de líquido en una botella

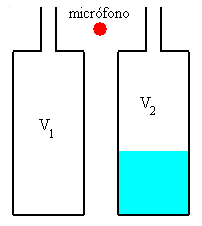
Consideremos dos botellas iguales con diferentes volúmenes de aire V₁ y V₂. Las frecuencias de resonancia serán respectivamente.

${\displaystyle {\omega }_1=c\sqrt{\frac{S}{L_e{V}_1}}{\omega }_2=c\sqrt{\frac{S}{L_e{V}_2}}}$

• S es el área de la sección del cuello

• V_1,2 es el volumen de aire en las botellas

• L_e es la longitud efectiva del cuello

• c es la velocidad del sonido en el aire

El cociente entre las dos frecuencias depende únicamente de sus volúmenes

${\displaystyle \frac{{\omega }_1}{{\omega }_2}=\sqrt{\frac{V_2}{V_1}}}$

Midiendo las frecuencias de resonancia ω₁ y ω₂, conocido el volumen de la botella vacía V₁ se determina el volumen V₂ de aire en la segunda botella.

Situamos un micrófono a igual distancia de las dos botellas y conectamos el micrófono a la tarjeta de sonido de un ordenador. Soplamos simultáneamente en las dos botellas y observamos en la pantalla del ordenador la superposición de los dos movimientos ondulatorios procedentes de cada una de las botellas en la posición del micrófono. Como el micrófono está a igual distancia de las bocas de las dos botellas supondremos que las amplitudes son iguales.

En la posición del micrófono, tendremos la superposición de dos Movimientos Armónicos Simples (MAS) de la misma amplitud A pero de distinta frecuencia.

ψ₁=Asin(ω₁·t)
ψ₂=Asin(ω₂·t)

El MAS resultante es

${\displaystyle \Psi =2A\cos \left(\frac{{\omega }_2-{\omega }_1}{2}t\right)\text{sin}\left(\frac{{\omega }_2+{\omega }_1}{2}t\right)}$

Cuya amplitud depende del tiempo (el primer factor coseno), y cuya frecuencia es la media aritmética de las dos frecuencias ω₁ y ω₂

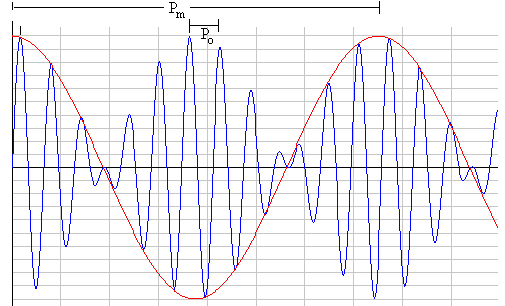
Medimos

• el periodo P₀ de una oscilación (en color azul), el intervalo de tiempo entre dos picos o dos valles consecutivos.

• el periodo P_m de la amplitud modulada (en color rojo)

${\displaystyle \begin{array}{l}{P}_0=\frac{4\pi }{{\omega }_2+{\omega }_1}{P}_m=\frac{4\pi }{{\omega }_2-{\omega }_1}\\ {\omega }_1=2\pi \left(\frac{1}{P_0}-\frac{1}{P_m}\right){\omega }_2=2\pi \left(\frac{1}{P_0}+\frac{1}{P_m}\right)\\ \frac{{\omega }_2}{{\omega }_1}=\frac{P_m+P_o}{P_m-P_0}\end{array}}$

Despejamos el volumen V₂ conocido el volumen V₁

${\displaystyle V_2={\left(\frac{P_m-P_0}{P_m+P_0}\right)}^2{V}_1}$

Ejemplo

El volumen V₁ de la botella vacía es 0.7 litros

h=0.2; %altura del fluido 
H=0.7;  %altura de la botella
cte=646; %engloba: la velocidad del sonido, sección 
del cuello de botella, sección de la botella cilíndrica
t=0:0.0002:0.1;
x=cos(cte*t*(-1/sqrt(H)+1/sqrt(H-h))/2).
*sin(cte*t*(1/sqrt(H)+1/sqrt(H-h))/2);
x1=cos(cte*t*(-1/sqrt(H)+1/sqrt(H-h))/2);
plot(t,x,t,x1);
grid on
ylim([-1.05,1.05])
xlabel('t')
ylabel('x')
title('Volumen de una botella')

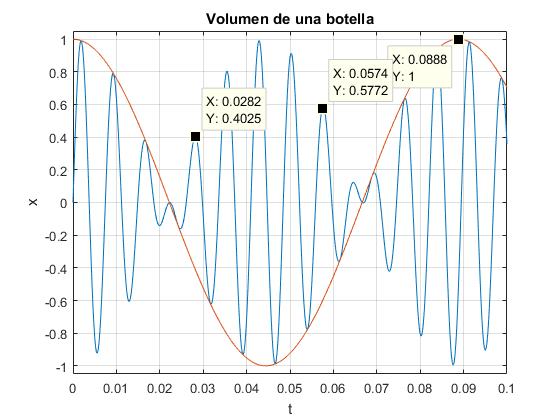
Medimos

• el periodo de varias oscilaciones (cuatro). El periodo P₀ de una oscilación (en color azul), P₀=(0.0574-0.0282)/4=0.0073 s

• el periodo P_m de la amplitud modulada (en color rosa), P_m=0.0888 s

${\displaystyle V_2={\left(\frac{0.0888-0.0073}{0.0888+0.0073}\right)}^{2}0.7=0.50}$

El volumen de líquido en la botella es 0.7-0.50=0.20

Actividades

• Se establece el volumen del líquido en la segunda botella en el control titulado Altura

• La primera botella está vacía, su volumen es de 0.7  litros.

Se pulsa el botón titulado Nuevo

Se observa en la la composición de los dos MAS de la misma dirección y distinta frecuencia (en color azul).

1. Se mide el tiempo de varias oscilaciones y se determina el periodo P₀ de una oscilación.

2. Se mide el periodo P_m de la amplitud.

Referencias

Alba J., Ramis J., Martínez J. A., Pico R., Escuder E., Aplicación de los fenómenos ondulatorios de batido y resonancia para la determinación del volumen de líquido en una botella. Revista Española de Física, V 18, nº 3, 2004, págs. 51-53