El regulador centrífugo está constituido por cuatro barras articuladas de masa despreciable y de la misma longitud l, que giran alrededor de un eje vertical, estando el sistema de barras fijado al punto B. El cuerpo de masa M que puede deslizar sin rozamiento a lo largo del eje, está apoyado en un resorte de constante k. Las bolas en las articulaciones A de las barras son iguales y de masa m. Cuando el sistema está en reposo C coincide con O y BO mide 2l.

• Calcular la deformación del resorte cuando el sistema gira con velocidad angular ω.

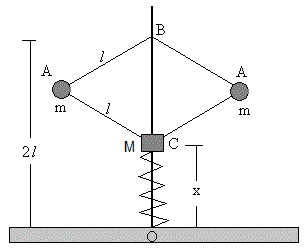
Formularemos la ecuación de la dinámica de cada una de las dos bolas y el equilibrio del cuerpo M que desliza a lo largo del eje.

• Movimiento de la bola



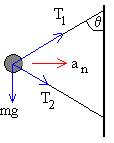
La bola describe un movimiento circular de radio l cosθ , siendo θ el ángulo formado por las barras y la horizontal. La aceleración normal de la bola es

a_n=ω²lsinθ

Por otra parte, la bola está en equilibrio en la dirección vertical.

Las ecuaciones que describen la dinámica de la bola son:

T₁sinθ+T₂sinθ=ma_n
T₁cosθ=T₂cosθ+mg

• Equilibrio del cuerpo que desliza a lo largo del eje



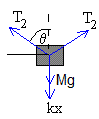
El cuerpo que desliza a lo largo del eje está en equilibrio, la resultante de las fuerzas que actúan sobre el mismo es cero.

2T₂cosθ=kx+Mg

Ahora relacionamos el ángulo θ con x.



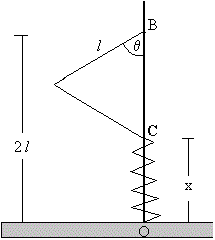
La relación entre el ángulo θ  con x y l, tal como se deduce de la figura, es

2lcosθ+x=2l

De las ecuaciones que describen la dinámica del sistema se despeja el valor de x.

${\displaystyle x=2\frac{m{\omega }^{2}l-mg-Mg}{m{\omega }^2+2k}}$

El valor x de la deformación del muelle viene señalado en una regleta por una flecha.

Ejemplo

Calcular la deformación del muelle x, con los datos siguientes del regulador centrífugo

El resultado es

${\displaystyle x=2\frac{1.5·{15}^2·0.6-1.5·9.8-2.5·9.8}{1.5·{15}^2+2·310}=0.34\text{m}=34\text{cm}}$

Actividades

Se introduce

• La constante elástica del muelle, en el control de edición titulado Constante muelle.
• La velocidad angular de rotación, actuando sobre la barra de desplazamiento o introduciendo un valor en el control de edición titulado Velocidad angular.
• La longitud de la varilla está fijada en l=0.6 m
• La masa del bloque que desliza está fijada en M=2.5 kg
• La masa de cada una de las bolas está fijada en m=1.5 kg

Se pulsa el botón titulado Nuevo

El regulador centrífugo empieza a girar, y una flecha marca sobre una regleta la deformación del muelle.

Comprobar que el resultado proporcionado por el programa interactivo, coincide con el obtenido al resolver el problema aplicando las ecuaciones que describen el equilibrio del cuerpo deslizante y la dinámica del movimiento circular de la bola.

Dinámica del regulador centrífugo

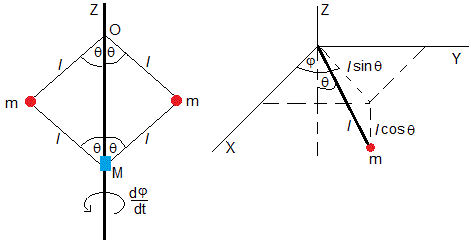
En esta versión del regulador centrífugo, eliminamos el muelle elástico y consideramos el movimiento de las dos bolas de masa m unidas mediante varillas de longitud l y de masa despreciable a la masa deslizante M, tal como se muestra en la figura. El sistema gira alrededor del eje Z con velocidad angular dφ/dt que no es constante

En la figura de la derecha, se muestra la posición de una bola de masa m situando el origen en el extremo superior del regulador, O y el eje Z es el eje del regulador. Las coordenadas de la bola de la derecha son

${\displaystyle \{\begin{array}{l}z=-l\cos \theta \\ x=l\sin \theta \cos \phi \\ y=l\sin \theta \sin \phi \end{array}}$

El ángulo φ es el ángulo de giro del regulador alrededor del eje Z. Derivando con respecto al tiempo, obtenemos las componentes de su velocidad

${\displaystyle \{\begin{array}{l}\frac{dz}{dt}=l\sin \theta \frac{d\theta }{dt}\\ \frac{dx}{dt}=l\cos \theta \cos \phi \frac{d\theta }{dt}-l\sin \theta \sin \phi \frac{d\phi }{dt}\\ \frac{dy}{dt}=l\cos \theta \sin \phi \frac{d\theta }{dt}+l\sin \theta \cos \phi \frac{d\phi }{dt}\end{array}}$

La energía cinética de esta partícula es

${\displaystyle E_1=\frac{1}{2}m\left({\left(\frac{dx}{dt}\right)}^2+{\left(\frac{dy}{dt}\right)}^2+{\left(\frac{dz}{dt}\right)}^2\right)=\frac{1}{2}m\left(l^2{\left(\frac{d\theta }{dt}\right)}^2+l^2{\sin }^2\theta {\left(\frac{d\phi }{dt}\right)}^2\right)}$

La energía cinética E₂ de la bola simétrica de masa m, es idéntica

La masa deslizante M se mueve a lo largo del eje Z, su posición y velocidad son

${\displaystyle \begin{array}{l}z=-l\cos \theta \\ \frac{dz}{dt}=l\sin \theta \frac{d\theta }{dt}\end{array}}$

Su energía cinética es

${\displaystyle E_3=2M{l}^2{\sin }^2\theta {\left(\frac{d\theta }{dt}\right)}^2}$

La energía cinética total E₁+E₂+E₃ del sistema de tres masas es

${\displaystyle E_k=m\left(l^2{\left(\frac{d\theta }{dt}\right)}^2+l^2{\sin }^2\theta {\left(\frac{d\phi }{dt}\right)}^2\right)+2M{l}^2{\sin }^2\theta {\left(\frac{d\theta }{dt}\right)}^2}$

La energía potencial es

${\displaystyle E_p=-2mgl\cos \theta -Mg\left(2l\cos \theta \right)=-2(m+M)gl\cos \theta }$

La lagrangiana L=E_k-E_p

${\displaystyle L=m\left(l^2{\left(\frac{d\theta }{dt}\right)}^2+l^2{\sin }^2\theta {\left(\frac{d\phi }{dt}\right)}^2\right)+2M{l}^2{\sin }^2\theta {\left(\frac{d\theta }{dt}\right)}^2+2(M+m)gl\cos \theta }$

La primera ecuación del movimiento es

${\displaystyle \begin{array}{l}\frac{d}{dt}\left(\frac{\partial L}{\partial \dot{\phi }}\right)-\frac{\partial L}{\partial \phi }=0\\ \frac{d}{dt}\left(2l^2{\sin }^2\theta \frac{d\phi }{dt}\right)=0\\ {\sin }^2\theta \frac{d\phi }{dt}=c\end{array}}$

Hay una magnitud que se mantiene constante. Supongamos que en un instante dado t, la velocidad angular de rotación es ω₀ y el ángulo que hacen las varillas con el eje es θ₀, entonces, ${\omega }_0{\sin }^2{\theta }_0=c$

La otra ecuación del movimiento es

${\displaystyle \begin{array}{l}\frac{d}{dt}\left(\frac{\partial L}{\partial \dot{\theta }}\right)-\frac{\partial L}{\partial \theta }=0\\ 2\left(m+2M{\sin }^2\theta \right)l\frac{d^2\theta }{d{t}^2}+2Ml\sin 2\theta {\left(\frac{d\theta }{dt}\right)}^2-ml\sin 2\theta {\left(\frac{d\phi }{dt}\right)}^2+2(M+m)g\sin \theta =0\end{array}}$

Combinando ambas ecuaciones obtenemos una ecuación diferencial en θ

${\displaystyle \left(m+2M{\sin }^2\theta \right)l\frac{d^2\theta }{d{t}^2}+Ml\sin 2\theta {\left(\frac{d\theta }{dt}\right)}^2-ml{c}^2\frac{\cos \theta }{{\sin }^3\theta }+(M+m)g\sin \theta =0}$

Equilibrio

La situación de equilibrio está dada por d²θ/dt²=0, dθ/dt=0

${\displaystyle \begin{array}{l}ml{c}^2\frac{\cos {\theta }_0}{{\sin }^3{\theta }_0}=(M+m)g\sin {\theta }_0\\ ml{\omega }_0^2{\sin }^4{\theta }_0\frac{\cos {\theta }_0}{{\sin }^3{\theta }_0}=(M+m)g\sin {\theta }_0\\ \cos {\theta }_0=\frac{(M+m)g}{ml{\omega }_0^2}\end{array}}$

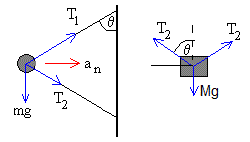
Las ecuaciones del movimiento de la bola son

T₁sinθ+T₂sinθ=ma_n
T₁cosθ=T₂cosθ+mg

con a_n=ω²lsinθ

La ecuación de equilibrio del cuerpo que desliza a lo largo del eje

2T₂cosθ=Mg

Dada la velocidad angular de rotación del dispositivo, ω₀ despejamos el ángulo de equilibrio θ₀ eliminando T₁ y T₂ en el sistema de ecuaciones

Movimiento alrededor de la posición de equilibrio

Si solamente estamos interesados en el ángulo θ que forman las varillas con el eje, resolvemos la segunda ecuación diferencial por procedimientos numéricos, con las siguientes condiciones iniciales, t=0, θ=θ₀+Δθ, dθ/dt=0.

Determinamos el valor de la constante c, conocida la posición de equilibrio θ₀ y estableciendo una velocidad angular de rotación ω₀

${\displaystyle c={\omega }_0{\sin }^2{\theta }_0}$

l=0.6; %longitud varilla
w0=15; %velocidad angular inicial de rotación
m=1.5; %bolas
M=2.5; %masa deslizante
th_0=acos((M+m)*9.8/(m*l*w0^2)); %ángulo de equilibrio
Dth=10*pi/180; %se desvía 10 grados de la posición de equilibrio
c=w0*sin(th_0)^2; %constante del movimineto
 
f=@(t,x)[x(2); (-M*sin(2*x(1))*x(2)^2+m*c^2*cos(x(1))/sin(x(1))^3-
(M+m)*9.8*sin(x(1))/l)/(m+2*M*sin(x(1))^2)];
[t,x]=ode45(f,[0,5],[th_0+Dth,0]); 

plot(t,x(:,1))
line([0,5],[th_0,th_0], 'lineStyle','--','color','k')
grid on
xlabel('t')
ylabel('\theta');
title('regulador centrífugo')
 
figure
plot(t,c./sin(x(:,1)).^2)
line([0,5],[w0,w0], 'lineStyle','--','color','k')
grid on
xlabel('t')
ylabel('d\phi/dt');
title('Velocidad angular de rotación')

Comprobamos que la energía del sistema E_k+E_p se mantiene constante

>> dphi=c./sin(x(:,1)).^2; 
>> E=m*l^2*x(:,2).^2+m*l^2*(sin(x(:,1)).^2).*dphi.^2+2*M*l^2*
(sin(x(:,1)).^2).*x(:,2).^2-2*(M+m)*9.8*l*cos(x(:,1))
E =
  111.6571
  111.6571
  111.6571
  ......

Representamos la posición θ en función del tiempo t. Se trata de una oscilación alrededor de la posición de equlibrio θ₀=1.376 rad, con amplitud de Δθ=10·π/180 (10°). La línea a trazos señala la posición de equilibrio θ₀

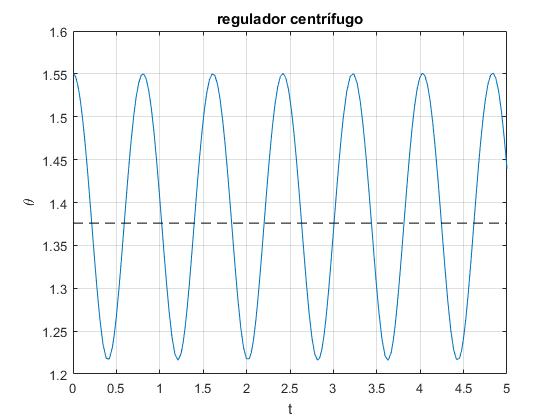
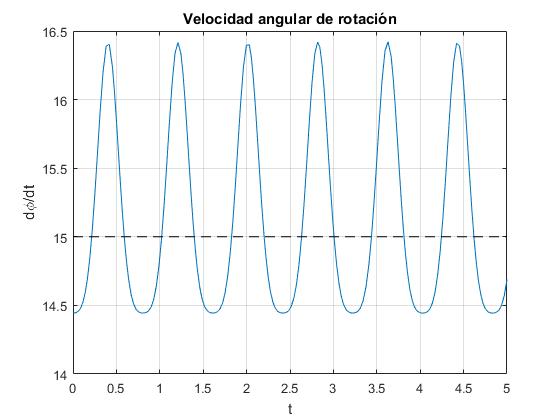
Conocida la posición angular θ(t), obtenemos la velocidad angular de rotación alrededor del eje Z, dφ/dt=c/sin²θ. La línea a trazos señala la velocidad angular de rotación ω₀

Referencias

Para el último apartado

Lim Yung-kuo. Problems and Solutions on Mechanics. World Scientific (1994). Problem 2064, pp. 610-612