Curva sin peralte

Un automóvil describe una trayectoria circular de radio R con velocidad constante v.

Suponemos que el vehículo describe una trayectoria circular de radio R con velocidad constante v. Para un observador inercial, situado fuera del vehículo, las fuerzas que actúan sobre el móvil son:

• el peso
• la reacción de la carretera
• la fuerza de rozamiento.

Esta última, es la que hace que el vehículo describa una trayectoria circular.

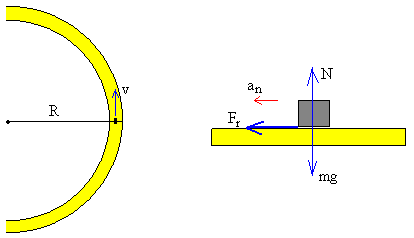
Como hay equilibrio en sentido vertical la reacción del plano es igual al peso

N=mg

Aplicando la segunda ley de Newton al movimiento en la dirección radial

${\displaystyle F_r=m{a}_n{F}_r=m\frac{v^2}{R}}$

Siendo v la velocidad del móvil y R el radio de la circunferencia que describe

A medida que se incrementa la velocidad v, se incrementa la fuerza de rozamiento F_r hasta que alcanza un valor máximo dado por el producto del coeficiente estático por la reacción del plano, μ·N.

La velocidad máxima v que puede alcanzar el vehículo para que describa una curva circular de radio R es, por tanto

${\displaystyle m\frac{v^2}{R}=\mu Nv=\sqrt{\mu gR}}$

Como apreciamos en el programa interactivo, a medida que se aumenta la velocidad del móvil, la fuerza de rozamiento crece hasta alcanzar el valor máximo μ·N, la trayectoria del vehículo es una circunferencia.

Si la velocidad del móvil es superior a la máxima, la fuerza de rozamiento, que es perpendicular al vector velocidad, tiene un valor constante e igual a su valor máximo, la trayectoria del móvil deja de ser circular. Para simplificar el problema hemos supuesto que los coeficientes estático y cinético tienen el mismo valor.

Curva con peralte

Consideremos ahora el caso de que la curva tiene un peralte de ángulo θ.

Las fuerzas que actúan sobre el cuerpo son las mismas que en el caso de la curva sin peralte, pero con distinta orientación salvo el peso.

• El peso mg
• La fuerza de rozamiento F_r
• La reacción del plano N

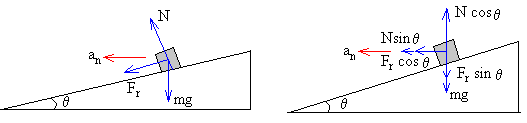
En la figura de la izquierda, se muestran las fuerzas y en la figura de la derecha, se ha sustituido la fuerza de rozamiento F_r y la reacción del plano N por la acción simultánea de sus componentes rectangulares.

La trayectoria que describe el vehículo es una sección cónica cortada por un plano perpendicular al eje del cono y por tanto, el centro de dicha circunferencia está situada en dicho plano y no en el vértice del cono.

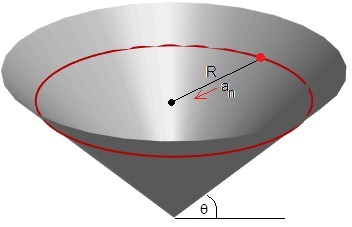
Para producir esta figura se ha empleado el siguiente código

theta=pi/6;
r=linspace(0,1,30);
phi=linspace(0,2*pi,30);
[r,phi]=meshgrid(r,phi);
x=r.*cos(phi)*sin(theta);
y=r.*sin(phi)*sin(theta);
z=r*cos(theta);
surfl(x,y,z);
shading interp
colormap(gray);

%circunferencia
phi=0:0.1:2*pi;
R=0.8;
x=R*cos(phi)*sin(theta);
y=R*sin(phi)*sin(theta);
z=R*cos(theta).*ones(1,length(x));
h1=line(x,y,z);
set(h1,'Color',[.7,0,0],'LineWidth',1.5)
axis off

• En el eje vertical no hay aceleración, tenemos una situación de equilibrio

Ncosθ=F_rsinθ+mg

• En el eje horizontal, aplicamos la segunda ley de Newton para el movimiento circular uniforme

Nsinθ+F_rcosθ=mv²/R

El vehículo comienza a deslizar hacia arriba en la dirección radial, cuando lleva una velocidad tal que F_r=μN. En el sistema de dos ecuaciones

N(cosθ-μsinθ)=mg
N(sinθ+μcosθ)=mv²/R

despejamos la velocidad máxima v que puede llevar el vehículo para que describa la curva con seguridad

${\displaystyle \frac{v^2}{Rg}=\frac{\sin \theta +\mu \cos \theta }{\cos \theta -\mu \sin \theta }}$

Ejemplo

Un coche circula por la curva de una carretera de 500 m de radio. Sabiendo que el coeficiente de rozamiento entre las ruedas del automóvil y el asfalto seco es de 0.75, calcular la máxima velocidad con el que el automóvil puede describir la curva con seguridad en los casos siguientes:

• la curva no tiene peralte

• la curva tiene un peralte de 15º

${\displaystyle \begin{array}{l}v=\sqrt{500·9.8·0.75}=60.6\text{m/s}\\ v=\sqrt{500·9.8\frac{\sin 15+0.75·\cos 15}{\cos 15-0.75·\sin 15}}=79.0\text{m/s}\end{array}}$

Cuando el ángulo del peralte es grande o el coeficiente de rozamiento pequeño

Consideremos ahora el caso en el que el coeficiente de rozamiento es pequeño o el ángulo de la curva es grande. Cuando se cumple que

mg·sinθ>μ·N, es decir, tanθ>μ.

Existirá una velocidad mínima v_mín de modo que el vehículo no deslice hacia abajo.

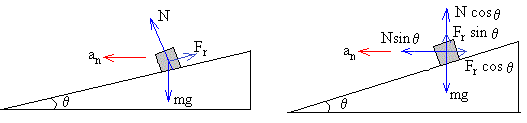
• En el eje vertical no hay aceleración, tenemos una situación de equilibrio

Ncosθ+F_rsinθ=mg

• En el eje horizontal, aplicamos la segunda ley de Newton para el movimiento circular uniforme

Nsinθ-F_rcosθ=mv²/R

El vehículo comienza a deslizar hacia abajo en la dirección radial, cuando lleva una velocidad tal que F_r=μN. En el sistema de dos ecuaciones

N(cosθ+μsinθ)=mg
N(sinθ-μcosθ)=mv²/R

Despejamos la velocidad mínima v_mín que puede llevar el vehículo para que describa la curva con seguridad

${\displaystyle \frac{v^2}{Rg}=\frac{\sin \theta -\mu \cos \theta }{\cos \theta +\mu \sin \theta }}$

El radio de la pista es R=500 m. Para el ángulo θ=15° y el coeficiente de rozamiento μ=0.2, se cumple que tanθ>μ.

• Para que no deslice hacia abajo: v_mín=17.8 m/s
• Para que no deslice hacia arriba: v_máx=49.2 m/s

Para que el vehículo circule con seguridad por una pista circular con peralte θ y coeficiente estático μ, se tiene que cumplir que

${\displaystyle \frac{\sin \theta -\mu \cos \theta }{\cos \theta +\mu \sin \theta }\le \frac{v^2}{Rg}\le \frac{\sin \theta +\mu \cos \theta }{\cos \theta -\mu \sin \theta }}$

Corresponde a la región sombreada de la figura

mu=0.2; %coeficiente estático
f=@(x) (sin(x)-mu*cos(x))./(cos(x)+mu*sin(x));
hold on
fplot(f, [atan(mu), pi/3])
g=@(x) (sin(x)+mu*cos(x))./(cos(x)-mu*sin(x));
fplot(g, [0, pi/3])
line([pi/12,pi/12],[f(pi/12), g(pi/12)],'color','k')
hold off
xlabel('\theta')
ylabel('v^2/(Rg)')
grid on
set(gca,'XTick',0:pi/12:pi/3)
set(gca,'XTickLabel',{'0','\pi/12','\pi/6','\pi/4','\pi/3'})
title('Curva con peralte')

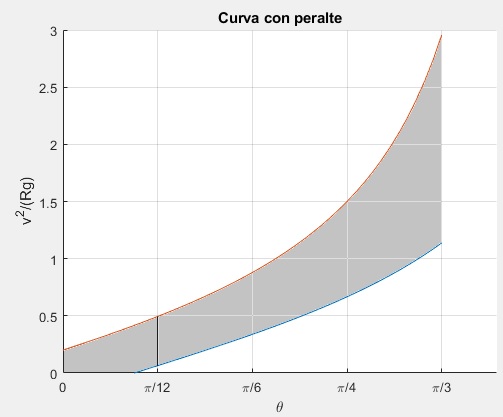
El ángulo inicial v=0, de la primera curva es tanθ=μ. Para μ=0.2, θ=11.3° (0.197 rad). Los extremos del segmento vertical para θ=15° (π/12), señalan el máximo y mínimo de v²/(Rg), calculados en el ejemplo anterior

Un vehículo a punto de volcar

Horizontal

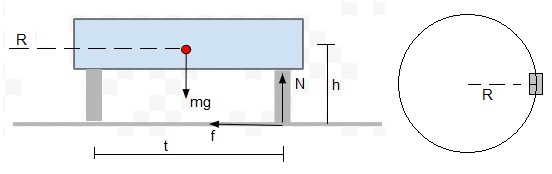
Consideremos un vehículo de masa m que describe una curva de radio R con velocidad constante v. La figura muestra el vehículo a punto de volcar.

• h es la altura del centro de masas del vehículo
• t es la distancia entre las ruedas opuestas
• N es la reacción de las ruedas exteriores
• f es la fuerza de rozamiento de las dos ruedas exteriores (no tiene por qué alcanzar el máximo valor μ_sN)

Las ecuaciones son

• El equilibrio en la dirección vertical, N=mg
• La ecuación de la dinámica del movimiento circular en la dirección horizontal, f=mv²/R
• Tomando momentos respecto del c.m, N(t/2)-fh=0

Eliminando, N y f

${\displaystyle \frac{t}{2h}=\frac{v^2}{Rg}}$

Ecuación que relaciona la geometría del vehículo (t, h) con la dinámica (v, R)

Cuando la distancia entre las ruedas t se incrementa el vehículo es más estable, cuando el centro de gravedad h está más cerca del suelo es tambien más estable

Sea t/(2h)=0.9. Si la curva tiene un radio R=10 m, la velocidad límite justo antes de volcar es v=9.39 m/s.

Inclinado

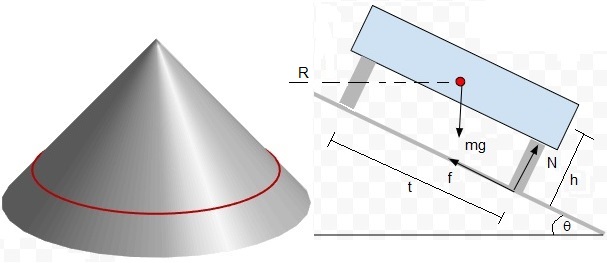
Supongamos que el vehículo circula por una superficie cónica tal como se muestra a la izquierda en la figura. Cortamos el cono por un plano vertical que pasa por el vértice y obtenemos la figura de la derecha

Para dibujar el cono se ha creado el script

theta=pi/6;
r=linspace(0,1,30);
phi=linspace(0,2*pi,30);
[r,phi]=meshgrid(r,phi);
x=r.*cos(phi)*sin(theta);
y=r.*sin(phi)*sin(theta);
z=-r*cos(theta);
surfl(x,y,z);
shading interp
colormap(gray);
 
%circunferencia
phi=0:0.1:2*pi;
R=0.8;
x=R*cos(phi)*sin(theta);
y=R*sin(phi)*sin(theta);
z=-R*cos(theta).*ones(1,length(x));
h1=line(x,y,z);
set(h1,'Color',[.7,0,0],'LineWidth',1.5)
axis off

• Equilibrio en la dirección vertical, Ncosθ+fsinθ=mg
• Aplicamos la dinámica del movimiento circular en la dirección horizontal, fcosθ-Nsinθ=mv²/R
• Momentos respecto del c.m., N(t/2)-fh=0

Eliminando, N y f

${\displaystyle \frac{\frac{t}{2h}-\tan \theta }{\frac{t}{2h}\tan \theta +1}=\frac{v^2}{Rg}}$

Supongamos un vehículo que circula por una curva de radio R=10 m, a una velocidad v, sus ruedas interiores se encuentran con un obstáculo que hace que el vehículo se incline un ángulo θ=5°. Sea t/(2h)=0.9, la velocidad crítica para esta situación es v=8.59 m/s

Tiovivo

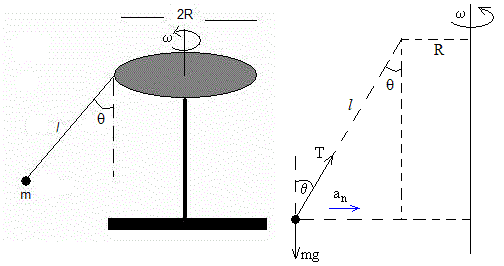
Un juego de un parque de atracciones consta de una plataforma circular de radio R m que gira con velocidad angular constante ω. De la plataforma cuelgan “sillas voladoras” suspendidas de unas cadenas de longitud l. Cuando la plataforma gira las cadenas que sostienen los asientos forman un ángulo θ con la vertical.

Formulamos el equilibrio en la dirección vertical y la dinámica del movimiento circular uniforme en la dirección horizontal

Tcosθ=mg
Tsinθ=mω²(R+l·sinθ)

Eliminando la tensión T

${\displaystyle \tan \theta =\frac{R{\omega }^2}{g}+\frac{l{\omega }^2}{g}\sin \theta }$

Mediante el cambio de variable

${\displaystyle t=\tan \frac{\theta }{2}\tan \theta =\frac{2t}{1-t^2}\sin \theta =\frac{2t}{1+t^2}}$

obtenemos la ecuación

${\displaystyle \frac{R{\omega }^2}{g}{t}^4+2\left(1+\frac{l{\omega }^2}{g}\right)t^3+2\left(1-\frac{l{\omega }^2}{g}\right)t-\frac{R{\omega }^2}{g}=0}$

Ejemplo

• Radio de la plataforma, R=4 m
• Longitud del péndulo, l=2.5 m
• Velocidad angular de rotación, ω=1 rad/s

R=4; %radio plataforma
l=2.5; %longitud del péndulo
w=1; %velocidad angular
p=[R*w^2/9.8,2*(1+l*w^2/9.8),0,2*(1-l*w^2/9.8),-R*w^2/9.8];
angulo=roots(p);
for k=1:length(angulo) 
    if isreal(angulo(k))
        if angulo(k)>0
            fprintf('El ángulo es %2.1f\n',2*atan(angulo(k))*180/pi)
            break;
        end
    end  
end 

El ángulo es 27.8

Referencias

Del apartado titulado 'Un vehículo a punto de volcar'

Desmond N. Penny. Rollover of sport utility vehicles The Physics Teacher, Vol 42, February, 2004, pp. 86-91