Equilibrio de una barra
Momento de una fuerza
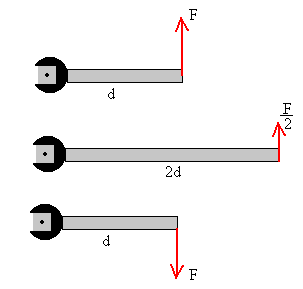
Supongamos que tenemos tres llaves que actúan sobre tres tornillos en la forma indicada por las figuras. Se aplica una fuerza F en el extremo de la llave. Es fácil contestar a las siguientes preguntas:
- ¿En qué situaciones se enrosca el tornillo?
- ¿En que situaciones se desenrosca el tornillo?
- ¿Cuáles producen el mismo resultado o son equivalentes?.
En la primera figura, el tornillo avanza en una dirección perpendicular al plano de la página, y hacia el lector. El módulo del momento es F·d.
En la segunda figura, el tornillo avanza en la misma dirección y sentido. El módulo del momento es F/2·(2d)=F·d. Con una llave más larga estamos en una situación más favorable que con una llave más corta.
En la tercera figura, el tornillo avanza en la misma dirección pero en sentido contrario.
- Un momento se considera positivo, si el tornillo sale, avanza hacia el lector, la llave gira en sentido contrario al movimiento de las agujas del reloj.
- Un momento se considera negativo, si el tornillo entra, la llave gira en el sentido del movimiento de las agujas del reloj.
Se denomina momento de una fuerza respecto de un punto, al producto vectorial del vector posición de la fuerza por el vector fuerza .
El vector tiene
- Por módulo, M=F·r·sinθ=F·d. Siendo del brazo de la fuerza (la distancia desde el punto O a la dirección de la fuerza)
- Dirección, perpendicular al plano determinado por la fuerza y el punto O.
- Sentido, la aplicación de la regla del sacacorchos
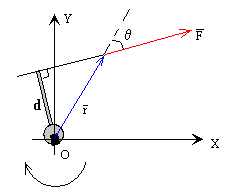
- El módulo es el producto de la fuerza F por la longitud d de la llave. M=F·r·sinθ=F·d
- La dirección, es la del eje del tornillo, eje Z
- El sentido viene determinado por el avance del tornillo (hacia dentro, negativo) cuando hacemos girar a la llave.
Ejemplos
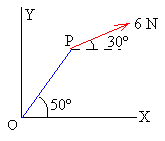
Hallar el momento (módulo dirección y sentido) de la fuerza F de módulo 6 N respecto del origen. El punto P de aplicación de la fuerza se encuentra a 45 cm del origen.
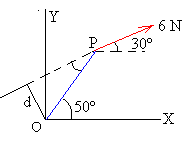
Brazo de la fuerza, d=0.45·sin20º
Equilibrio de una barra
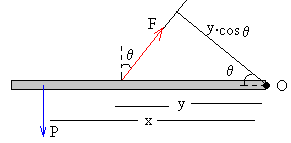
Supongamos una barra de masa despreciable, que está sujeta por su extremo O.
Si colocamos un peso P a una distancia x del origen. El momento de esta fuerza respecto del origen O es +P·x.
Atamos una cuerda a una distancia y del origen y tiramos de ella haciendo un ángulo θ con la vertical, tal como se muestra en la figura. El momento de la fuerza F respecto del origen es -F·y·cosθ.
Para que la barra esté en equilibrio, el momento total deberá ser nulo.
-F·y·cosθ+P·x=0
Actividades
Sea una barra de 50 cm de longitud, de masa despreciable, dispone de ganchos situados en las divisiones 0, 5, 10, ... 50 cm. La barra está sujeta por uno de sus extremos O.
Se introduce
- La posición y de la cuerda, en el control titulado Posición cuerda
- El ángulo θ que forma la cuerda con la vertical, en el control titulado Angulo cuerda.
Se pulsa el botón titulado Nuevo
Aparecen pesas de distintos colores de 10 g, 25 g y 50 g. Con el puntero del ratón arrastramos una pesa y la colgamos de la barra en alguno de los ganchos.
Cogemos otra pesa y la colgamos de otro gancho de la barra y así, sucesivamente, hasta un máximo de seis pesas (dos de cada tipo). Podemos colgar más de una pesa en la misma posición, una debajo de la otra.
Un dinamómetro nos mide la tensión F de la cuerda necesaria para mantener la barra horizontal y en equilibrio. La fuerza viene expresada en Newton (N).
- Primero, establecemos el ángulo de la cuerda θ=0, y probamos con una sola pesa colocándola en varias posiciones y anotamos la fuerza que señala el dinamómetro.
- Después, probamos con varias pesas en distintas posiciones coincidentes o no.
Se pulsa el botón titulado Nuevo, se coloca una pesa colgada de un gancho, se apunta el valor de la fuerza F que marca el dinamómetro. Se pulsa el botón Nuevo, se elige la misma pesa y se coloca en otro gancho y así sucesivamente.
Fijarse que las pesas situadas en el origen no ejercen momento alguno. Y aquellas que están situadas en el otro extremo de la barra ejercen un momento máximo.
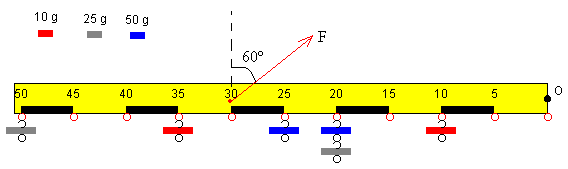
Colocamos las seis pesas tal como se muestra en la figura. Atamos un extremo de la cuerda en la posición y=30, formando un ángulo θ=60º con la vertical. Calcular la tensión F de la cuerda para que la barra se mantenga en posición horizontal y en equilibrio.
| Pesa (g) | Posición (cm) | Momento (g·cm) | |
|---|---|---|---|
| 10 | 35 | 10 | 450 |
| 25 | 50 | 20 | 1750 |
| 50 | 25 | 20 | 2250 |
| Total | 4450 | ||
El momento de la fuerza que ejerce la cuerda es
-F·y·cosθ=-F·30·cos60º=-F·15
La condición de equilibrio se escribe
-F·15+4450=0 F=296.67 g
Expresamos la fuerza en N multiplicando por 9.8 y dividiendo por 1000
F=2.91 N
Medida de la densidad de un líquido
En la página titulada 'Medida de la densidad de un líquido y de un sólido', se describe un procedimiento para la medida de la densidad de un líquido que se fundamenta en el principio de Arquímedes.
En este apartado, vamos a mostrar otro procedimiento que se fundamenta en el equilibrio de dos cuerpos que cuelgan de un barra (balanza) apoyada en su punto medio. El procedimiento consta de tres pasos que se muestran en la figura:
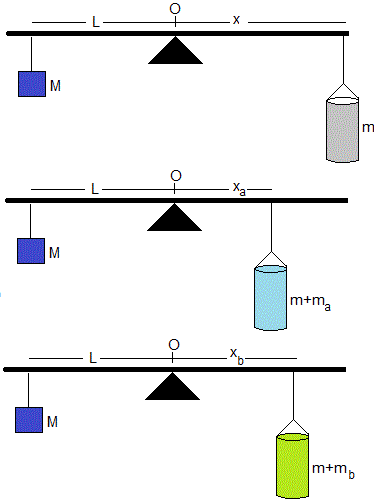
Se equilibra un cuerpo de masa M desconocida con un recipiente vacío de masa m desconocida. En el equilibrio,
Se llena un volumen V del recipiente con una masa ma de líquido de densidad conocida, por ejemplo el agua, cuya densidad es ρa=ma/V. En el equilibrio
Se sustituye el agua por el mismo volumen V de líquido de densidad desconocida ρb=mb/V, donde mb es la masa de este volumen V de líquido. En el equilibrio
MgL=mgx
Donde L es el brazo del cuerpo de masa desconocida y x el brazo del recipiente vacío
MgL=(m+ma)gxa
MgL=(m+mb)gxb
Eliminando las cantidades desconocidas, la masa M del sólido y la masa m del recipiente vacío. Obtenemos la relación
Dividiendo, las masas entre el volumen V de agua o del líquido de densidad desconocida, obtenemos la relación entre las densidades.
Obtenemos la densidad desconocida ρb de un líquido, a partir de la densidad ρa del agua, midiendo los brazos x, xa y xb de la balanza en las tres situaciones de equilibrio, que se muestran en la figura.
Práctica de laboratorio
La primera experiencia consiste en colgar pesas de una barra hasta lograr el equilibrio
Como vemos en esta imagen, se ha colocado en la parte izquierda de la barra, una pesa a una unidad de distancia y otra pesa, a dos unidades de distancia. El momento, en unidades arbitrarias, es 1×1+1×2=3
En la parte derecha, se han colocado tres pesas a una unidad de distancia, el momento es 3×1=3

Como vemos en esta imagen, se ha colocado en la parte izquierda de la barra una pesa a tres unidades de distancia y dos pesas a dos unidades. El momento, en unidades arbitrarias, es 1×3+2×2=7
En la parte derecha, se han colocado dos pesas a una unidad de distancia, una pesa a dos unidades y otra pesa a tres unidades de distancia. El momento es 1×3+1×2+2×1=7

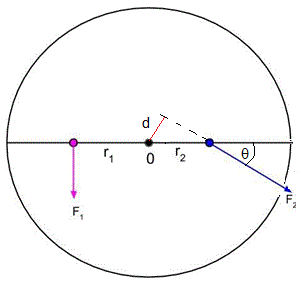
La segunda experiencia consiste en medir la fuerza necesaria para equilibrar un disco.
F1 representa un peso que se cuelga de la posición r1. F2 es la fuerza que tenemos que aplicar en la posición r2, haciendo un ángulo θ para equlibrar el disco, esta fuerza la mide un dinamómetro.
En el equilibrio, cuando el diámetro del disco está horizontal,
F1·r1 = F2·d
Siendo d el brazo de la fuerza, d=r2·sinθ
Medimos el ángulo θ, la fuerza F2 que marca el dinamómetro, convertimos el peso F1 de gramos a N, y medimos las distancias r1 y r2

| F1 (N) | r1 (m) | F2 (N) | r2 (m) | Angulo θ | d (m) | F1r1 | F2d |
|---|---|---|---|---|---|---|---|
| 1.078 | 0.06 | 1.1 | 0.12 | 30° | 0.06 | 0.065 | 0.066 |
| 0.588 | 0.06 | 0.8 | 0.1 | 25° | 0.042 | 0.035 | 0.034 |
Referencias
Medida de la densidad de un líquido
K N Chattopadhyay Finding the density of a liquid using a metre rule. Physics Eduacation, 43 (2) March 2008, pp.203-205

