Fuerza de rozamiento
Coeficientes estático y cinético
El rozamiento entre dos superficies en contacto ha sido aprovechado por nuestros antepasados más remotos para hacer fuego frotando maderas. En nuestra época, el rozamiento tiene una gran importancia económica, se estima que si se le prestase mayor atención se podría ahorrar muchísima energía y recursos económicos.
Históricamente, el estudio del rozamiento comienza con Leonardo da Vinci que dedujo las leyes que gobiernan el movimiento de un bloque rectangular que desliza sobre una superficie plana. Sin embargo, este estudio pasó desapercibido.
En el siglo XVII Guillaume Amontons, físico francés, redescubrió las leyes del rozamiento estudiando el deslizamiento seco de dos superficies planas. Las conclusiones de Amontons son esencialmente las que estudiamos en los libros de Física General:
- La fuerza de rozamiento se opone al movimiento de un bloque que desliza sobre un plano.
- La fuerza de rozamiento es proporcional a la fuerza normal que ejerce el plano sobre el bloque.
- La fuerza de rozamiento no depende del área aparente de contacto.
El científico francés Coulomb añadió una propiedad más
- Una vez empezado el movimiento, la fuerza de rozamiento es independiente de la velocidad.
Explicación del origen del rozamiento por contacto
La mayoría de las superficies, aún las que se consideran pulidas son extremadamente rugosas a escala microscópica. Los picos de las dos superficies que se ponen en contacto determinan el área real de contacto que es una pequeña proporción del área aparente de contacto (el área de la base del bloque). El área real de contacto aumenta cuando aumenta la presión (la fuerza normal) ya que los picos se deforman.
Los metales tienden a soldarse en frío, debido a las fuerzas de atracción que ligan a las moléculas de una superficie con las moléculas de la otra. Estas soldaduras tienen que romperse para que el deslizamiento se produzca. Además, existe siempre la incrustación de los picos con los valles. Este es el origen del rozamiento estático.
Cuando el bloque desliza sobre el plano, las soldaduras en frío se rompen y se rehacen constantemente. Pero la cantidad de soldaduras que hay en cualquier momento se reduce por debajo del valor estático, de modo que el coeficiente cinético es menor que el coeficiente estático.
Finalmente, la presencia de aceite o de grasa en las superficies en contacto evita las soldaduras al revestirlas de un material inerte.
La explicación de que es la siguiente:
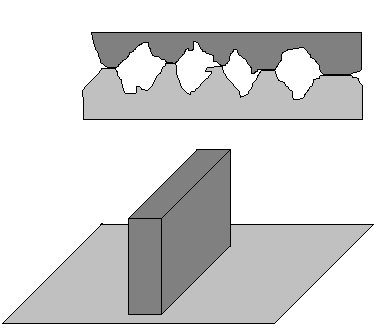
En la figura, la superficie más pequeña de un bloque está situada sobre un plano. En el dibujo situado arriba, vemos un esquema de lo que se vería al microscopio: grandes deformaciones de los picos de las dos superficies que están en contacto. Por cada unidad de superficie del bloque, el área de contacto real es relativamente grande (aunque esta es una pequeña fracción de la superficie aparente de contacto, es decir, el área de la base del bloque).
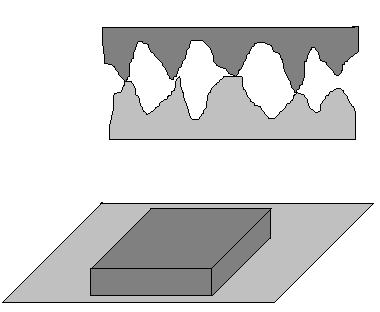
En la figura, la superficie más grande del bloque está situada sobre el plano. El dibujo muestra ahora que las deformaciones de los picos en contacto son ahora más pequeñas por que la presión es más pequeña. Por tanto, un área relativamente más pequeña está en contacto real por unidad de superficie del bloque. Como el área aparente en contacto del bloque es mayor, se deduce que el área real total de contacto es esencialmente la misma en ambos casos.
Ahora bien, las investigaciones actuales que estudian el rozamiento a escala atómica demuestran que la explicación dada anteriormente es muy general y que la naturaleza de la fuerza de rozamiento es muy compleja (Véase el artículo titulado "Rozamiento a escala atómica" en las Referencias de este capítulo.
La fuerza normal
La fuerza normal, reacción del plano o fuerza que ejerce el plano sobre el bloque depende del peso del bloque, la inclinación del plano y de otras fuerzas que se ejerzan sobre el bloque tal como vamos a ver en estos ejemplos.
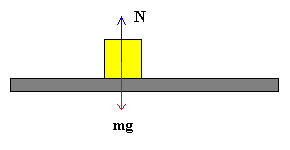
Supongamos que un bloque de masa m está en reposo sobre una superficie horizontal, las únicas fuerzas que actúan sobre él son el peso mg y la fuerza y la fuerza normal N. De las condiciones de equilibrio se obtiene que la fuerza normal N es igual al peso mg
N=mg
Si ahora, el plano está inclinado un ángulo θ , el bloque está en equilibrio en sentido perpendicular al plano inclinado por lo que la fuerza normal N es igual a la componente del peso perpendicular al plano, N=mg·cosθ
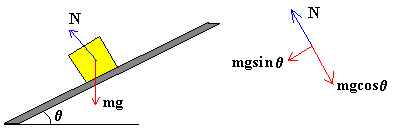
Consideremos de nuevo el bloque sobre la superficie horizontal. Si además atamos una
cuerda al bloque que forme un ángulo θ con la
horizontal, la fuerza normal deja de ser igual al peso. La condición de equilibrio en la
dirección perpendicular al plano establece
N+F·sinθ =mg
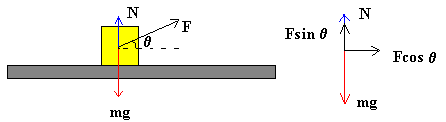
El bloque se mueve
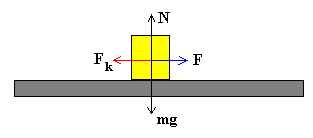
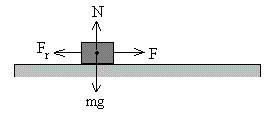
En la figura, se muestra un bloque arrastrado por una fuerza F horizontal. Sobre el bloque actúan el peso mg, la fuerza normal N que es igual al peso y la fuerza de rozamiento Fk entre el bloque y el plano sobre el cual desliza. Si el bloque desliza con velocidad constante la fuerza aplicada F será igual a la fuerza de rozamiento Fk.
Investigaremos la dependencia de Fk con la fuerza normal N. Veremos que si duplicamos la masa m del bloque que desliza colocando encima de éste otro igual, la fuerza normal N se duplica, la fuerza F con la que tiramos del bloque se duplica y por tanto, Fk se duplica.
La fuerza de rozamiento Fk es proporcional a la fuerza normal N.
Fk=μk N
La constante de proporcionalidad μk es un número sin dimensiones que se denomina coeficiente cinético de rozamiento.
El valor de μk es casi independiente del valor de la velocidad para velocidades relativas pequeñas entre las superficies y decrece lentamente cuando el valor de la velocidad aumenta.
El bloque está en reposo
También existe una fuerza de rozamiento entre dos objetos que no están en movimiento relativo.
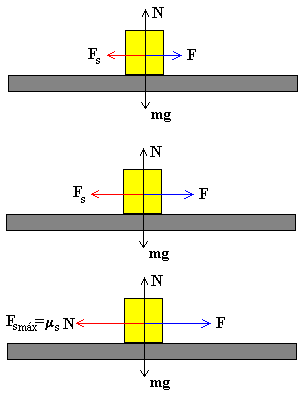
Como vemos en la figura, la fuerza F aplicada sobre el bloque aumenta gradualmente, pero el bloque permanece en reposo. Como la aceleración es cero la fuerza aplicada es igual y opuesta a la fuerza de rozamiento Fs.
F=Fs
La máxima fuerza de rozamiento se produce en el momento en el que el bloque comienza a deslizar.
Fs máx=μsN
La constante de proporcionalidad μs se denomina coeficiente estático.
Los coeficientes estático y cinético dependen de las condiciones de preparación y de la naturaleza de las dos superficies y son casi independientes del área de la superficie de contacto.
| Superficies en contacto | μs | μk |
| Cobre sobre acero | 0.53 | 0.36 |
| Acero sobre acero | 0.74 | 0.57 |
| Aluminio sobre acero | 0.61 | 0.47 |
| Caucho sobre concreto | 1.0 | 0.8 |
| Madera sobre madera | 0.25-0.5 | 0.2 |
| Madera encerada sobre nieve húmeda | 0.14 | 0.1 |
| Teflón sobre teflón | 0.04 | 0.04 |
| Articulaciones sinoviales en humanos | 0.01 | 0.003 |
Fuente: Serway R. A.. Física. Editorial McGraw-Hill. (1992)
Ejemplos
La fuerza de rozamiento entre dos cuerpos en contacto no es fácil de entender, por lo que en este apartado se resolverán varios ejemplos
Ejemplo 1
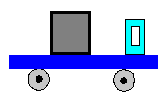
Una camioneta transporta un cajón de 20 kg. El cajón descansa sobre la plataforma de carga.
Estudiar la dinámica del cajón sobre la plataforma, determinando la fuerza de rozamiento entre el cajón y la plataforma y la aceleración del cajón, cuando la aceleración del camión tiene los siguientes valores. (Tomar g=10 m/s2)
- Está parado
- Lleva una aceleración de 3 m/s2.
- Lleva una aceleración de 7 m/s2.
- Lleva una aceleración de 8 m/s2.
- ¿Cuál es la máxima aceleración con que puede arrancar la camioneta en un semáforo sobre una calle horizontal, de forma que el cajón no deslice hacia atrás en la plataforma?
- Indíquese en los distintos casos la aceleración del cajón respecto del conductor del camión.
Datos: el coeficiente estático es 0.7 y el coeficiente cinético, 0.65.
Solución
La fuerza de rozamiento es una cuerda invisible que ata el cajón a la plataforma del camión. Si no hubiese rozamiento el cajón no podría desplazarse junto con la plataforma.
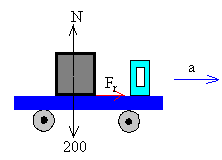
- Si está parado, las fuerzas sobre el cajón son:
- El peso 20·10 N
- La reacción de la plataforma, o fuerza que ejerce la plataforma sobre el cajón, N=200 N
- Si se mueve con una aceleración de 3 m/s2.
- Si se mueve con una aceleración de 7 m/s2.
- Si se mueve con una aceleración de 8 m/s2.
La fuerza de rozamiento (tensión de la cuerda invisible) que tira del cajón vale
Fr=20·3=60 N
La fuerza de rozamiento (tensión de la cuerda invisible) que tira del cajón vale
Fr=20·7=140 N
Este es el valor máximo de la fuerza de rozamiento, Frmax=μs·N=0.7·200=140 N, (esta es la máxima tensión que soporta la cuerda invisible). El cajón va a empezar a deslizar sobre la plataforma
El cajón desliza sobre la plataforma. La fuerza de rozamiento vale
Fr=μk·N=0.65·200=130 N
La aceleración del cajón vale
Fr=20·a, a=6.5 m/s2
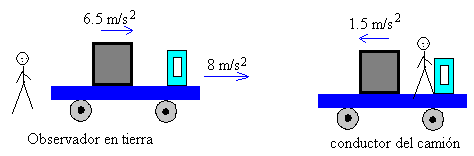
La aceleración del cajón es más pequeña que la aceleración de la plataforma. El cajón desliza sobre la plataforma con una aceleración relativa de 6.5-8=-1.5 m/s2.
Ejemplo 2

Colocamos un cuerpo de masa m sobre un plano cuyo ángulo de inclinación puede modificase. Calcular el ángulo θ del plano inclinado justo antes de que el cuerpo comience a deslizar.
Solución
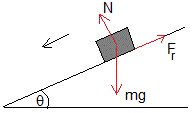
Sustituimos el peso mg por la acción simultánea de sus componentes a lo largo del plano y perpendicularmente al plano inclinado. En el equilibrio
La fuerza de rozamiento alcanza su valor máximo cuando Fr=μsN, para el ángulo
Datos, m=10 kg, μs=0.3 y μk=0.2
Tendremos que el ángulo crítico θc=16.7°. El máximo valor de la fuerza de rozamiento es μsN=28.9 N
Supongamos que el ángulo del plano inclinado es menor, θ=10°. La fuerza de rozamiento Fr=mgsinθ=17.0 N menor que la máxima. El cuerpo permenecerá en reposo sobre el plano inclinado
Supongamos que el ángulo del plano inclinado es mayor, θ=20°. De las ecuaciones de equilibrio, obtenemos la fuerza de rozamiento Fr=mgsinθ=33.5 N mayor que la máxima. El cuerpo desliza y la fuerza de rozamiento es Fr=μkN=18.6 N
Ejemplo 3
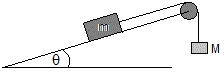
Un cuerpo de masa m descansa sobre un plano inclinado de ángulo θ. Está unido mediante una cuerda inextensible y de masa despreciable que pasa por una polea a otro cuerpo de masa M que cuelga.
Calcular el intervalo de valores de la masa M del cuerpo que cuelga para que el cuerpo de masa m se mantenga en equilibrio sobre el plano inclinado, es decir, no deslice hacia arriba ni hacia abajo.
Datos, m=10 kg, θ=30°, μs=0.3 y μk=0.2
Solución
Hacia arriba
Hacia abajo
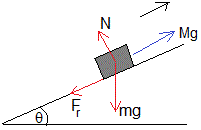
En el equilibrio
Cuando el cuerpo empieza a deslizar hacia arriba, la fuerza de rozamiento alcanza su valor máximo μsN=25.4 N
El valor máximo es Mmáx=7.6 kg
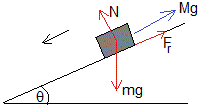
En el equilibrio
Cuando el cuerpo empieza a deslizar hacia abajo, la fuerza de rozamiento alcanza su valor máximo μsN
El valor mínimo es Mmín=2.4 kg
Examinamos ahora dos casos: la masa del cuerpo que cuelga M está en comprendida el intervalo (Mmáx, Mmín) y fuera de dicho intervalo
Sea M=6 kg. Calculamos el valor y sentido de la fuerza de rozamiento
-
Sea M=2 kg. Calculamos el valor y sentido de la fuerza de rozamiento
Supongamos que desliza hacia abajo, Fr=mgsinθ-Mg=-9.8 N. La fuerza de rozamiento es hacia abajo (de sentido contrario al supuesto inicialmente), como en la primera figura y es menor que el valor máximo (9.8<25.4), luego el cuerpo de masa m permanecerá en equilibrio, en reposo sobre el plano inclinado
Supongamos que desliza hacia abajo, Fr=mgsinθ-Mg=29.4 N. La fuerza de rozamiento es mayor que el valor máximo (25.4 N), luego, el cuerpo de masa m deslizará a lo largo del plano inclinado hacia abajo y la fuerza de rozamiento valdrá Fr=μkN=17.0 N
Ejemplo 4
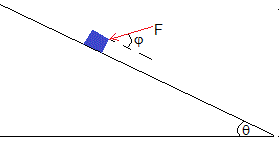
Un cuerpo de masa m descansa sobre un plano inclinado. El coeficiente estático es μs y el ángulo del plano inclinado es mayor que el crítico tanθc=μs. Esto implica (véase ejemplo 2) que tendremos que aplicar una fuerza F para mantener el cuerpo en equilibrio con el fin de impedir que deslice hacia abajo.
Se tratará de calcular el valor mínimo de F
Solución
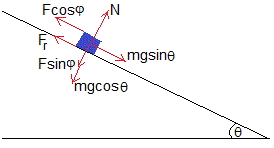
Las fuerzas sobre el cuerpo son
- La fuerza aplicada F formando un ángulo φ con el plano inclinado
- El peso del cuerpo, mg
- La reacción del plano inclinado, N
- La fuerza de rozamiento, Fr que se opone a que el cuerpo deslice hacia abajo
En la figura, se sustituyen las fuerzas por sus componentes a lo largo del plano inclinado y en la dirección perpendicular al plano inclinado. En la situación de equilibrio
Vamos a calcular la fuerza mínima F necesaria para mantener el cuerpo en equilibrio. Justo cuando va a empezar a deslizar hacia abajo, Fr=μsN. Despejamos la fuerza F aplicada del sistema de dos ecuaciones
Expresamos el denominador, de la forma kcos(φ-α)=kcosα·cosφ+ksinα·sinφ
La fuerza F se expresa
El valor mínimo de F es el máximo del denominador
Este valor se puede calcular, mediante derivadas. El extremo de una función (mínimo) es
Teniendo en cuenta las relaciones trigonométricas
Obtenemos el mismo resultado
Representamos F/(mg), sabiendo que el coeficiente estático vale μs=0.5, en función del ángulo φ, para tres valores de θ: 40°, 50°, 60°, 70°. El ángulo crítico es θc=arctan(μs)=26.6°
mu=0.5;
hold on
for th=(40:10:80)*pi/180
f=@(x) (sin(th)-mu*cos(th))./(cos(x)+mu*sin(x));
fplot(f, [0,pi/2])
end
phi_c=atan(mu);
line([phi_c,phi_c],[0,1])
hold off
xlabel('\phi')
ylabel('F/mg')
legend('40','50','60','70','80','location','best')
set(gca,'XTick',0:pi/12:pi/2)
set(gca,'XTickLabel',{'0','\pi/12','\pi/6','\pi/4','\pi/3','5\pi/12','\pi/2'})
grid on
title('Fuerza F aplicada')
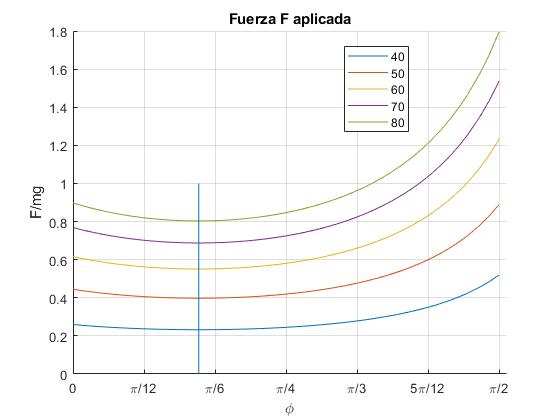
El ángulo φm señalado mediante una línea recta vertical, es independiente de θ, y es el mismo que el ángulo crítico θc, más allá del cual el cuerpo desliza en ausencia de la fuerza aplicada F
Comportamiento de un cuerpo que descansa sobre un plano horizontal
Dibujemos una gráfica en la que en el eje horizontal representamos la fuerza F aplicada sobre el bloque y en el eje vertical la fuerza de rozamiento.
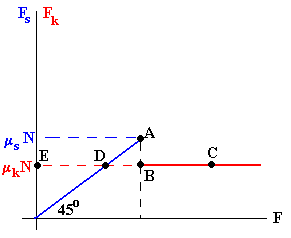
- Desde el origen hasta el punto A la fuerza F aplicada sobre el bloque no es suficientemente grande como para moverlo. Estamos en una situación de equilibrio estático
- Si la fuerza F aplicada se incrementa un poquito más, el bloque comienza a moverse. La fuerza de rozamiento disminuye rápidamente a un valor menor e igual a la fuerza de rozamiento por deslizamiento, Fk=μkN
F= Fs<μsN
En el punto A, la fuerza de rozamiento estático Fs alcanza su máximo valor μsN
F= Fs máx=μsN
Si la fuerza F no cambia, punto B y permanece igual a F=Fs máx el bloque se mueve con una aceleración
a=(F-Fk)/m
Si incrementamos la fuerza F, punto C, la fuerza neta sobre el bloque F-Fk se incrementa y también se incrementa la aceleración.
En el punto D, la fuerza F aplicada es igual a Fk por lo que la fuerza neta sobre el bloque será cero. El bloque se mueve con velocidad constante.
En el punto E, se anula la fuerza aplicada F, la fuerza que actúa sobre el bloque es - Fk, la aceleración es negativa y la velocidad decrece hasta que el bloque se detiene.
Experiencia
Un bloque de masa m descansa sobre un plano horizontal, el bloque está unido mediante un hilo inextensible y de peso despreciable que pasa por una polea a un platillo sobre el que se depositan pesas. Vamos a estudiar el comportamiento del bloque y a realizar medidas del coeficiente estático y cinético.
Medida del coeficiente estático
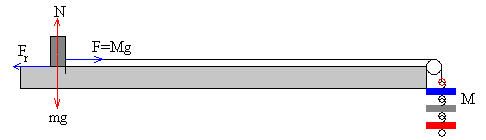
Se van colocando pesas en el platillo y el bloque permanece en reposo. La fuerza de rozamiento vale
Fr=Mg
donde M es la masa de las pesas que contiene el platillo
Cuando va a empezar a deslizar, la fuerza de rozamiento Fr adquiere el valor máximo posible μsN=μsmg
Medida del coeficiente cinético
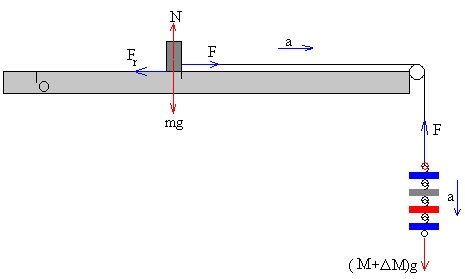
Añadimos una pesa más ΔM y el bloque empieza a deslizar, desplazándose una longitud x en un t. La aceleración es x=at2/2
Aplicamos la segunda ley de Newton al movimiento del bloque
F-Fr=ma
Fr=μk·N
N=mg
Aplicamos la segunda ley de Newton al movimiento del platillo y las pesas
(M+ΔM)g-F=(M+ΔM)a
Despejamos el coeficiente cinético μk
Actividades
El programa interactivo genera aleatoriamente un valor del coeficiente cinético de rozamiento μk. El coeficiente estático se ha tomado arbitrariamente como μs= μk+0.2.
Se introduce
- La masa del bloque en kg, en el control titulado Masa
Se pulsa el botón titulado Nuevo
Con el puntero del ratón se arrastra la pesa hasta que enganche debajo del extremo del hilo que cuelga de la polea.
A continuación, se agrega otra pesa debajo de la anterior y así sucesivamente, hasta que el bloque empiece a deslizar.
Medida del coeficiente estático
Para medir el coeficiente tenemos que acercarnos lo máximo posible al valor de la fuerza μsN que hace que el bloque comience a deslizar con el juego de pesas disponible. En este caso, se dispone de un total de 12 pesas, cuatro de cada tipo:
- 25 g
- 100 g
- 500 g
Ponemos un ejemplo, que nos indica la forma de acercarnos al valor máximo de la fuerza de rozamiento.
- Se pulsa el botón titulado Nuevo. Se empieza colocando una pesa de 500 g, el bloque no desliza. Se pone una segunda pesa de 500g, el bloque no desliza. Se añade la tercera pesa de 500 g, el bloque desliza
- Se pulsa el botón titulado Nuevo. Se pone dos pesas de 500 g. Se añade una pesa de 100 g, el bloque no desliza. Se añade la segunda pesa de 100 g, el bloque desliza.
- Se pulsa el botón titulado Nuevo. Se pone dos pesas de 500 g, y una pesa de 100 g. Se añade una pesa de 25 g, el bloque no desliza. Se añade la segunda pesa de 25 g, el bloque no desliza, se añade la tercera pesa de 25 g, el bloque desliza.
El valor de la fuerza F más cercana al valor máximo μsN (por defecto) es
F=(2·500+100+2·25)·10.0/1000 =11.5 N
La aceleración de la gravedad se ha tomado como g=10.0 m/s2
Si la masa del bloque es m=2 kg, N=mg=20 N. El coeficiente estático μs valdrá
μs=11.5/20=0.575
Medida del coeficiente cinético
Cuando añadimos la tercera pesa de ΔM=25 g, el bloque empieza a deslizar
La masa de las pesas que cuelgan es M+ΔM=1.15+0.025=1.175 kg
El bloque se desplaza x=1 m en t=1.22 s.
Práctica de laboratorio

En esta práctica de laboratorio, se mide el coeficiente estático y cinético con un sensor de fuerza
En el laboratorio disponemos de un recipiente de plástico que puede deslizar sobre la superficie horizontal de una mesa. La base del recipiente está recubierta de tela, aunque puede ser de otros materiales (plástico, corcho, etc).
En esta experiencia hacemos deslizar el recipiente de 96 g recubierto de tela sobre la superficie de la mesa recubierta por una hoja de papel, tal como puede apreciarse en la figura. En el interior del recipiente se colocan pesas de 250 g cada una. Se empuja el recipiente con el sensor de fuerza y el programa CAPSTONE muestra la siguiente gráfica
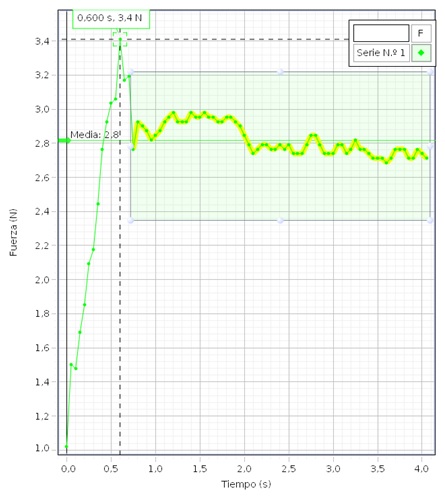
Con la herramienta, Agregar una herramienta de coordenadas medimos el máximo valor de la fuerza de rozamiento, Fs=3.4 N, cuando el cuerpo empieza a deslizar.
![]()
Cuando el cuerpo desliza, la fuerza de rozamiento disminuye y se mantiene casi constante. Calculamos y representamos con la herramienta Muestra estadística seleccionada, el valor medio, Fk=2.8 N, de los valores seleccionados de la fuerza con la herramienta Resalta el rango de puntos activos a la izquierda de la herramienta anterior.
![]()
Colocamos una pesa de 250 g en el recipiente, la masa total m=96+250=346 g. La reacción N=0.346·9.8=3.39 N. Medimos el máximo valor de la fuerza de rozamiento Fs, cuando el cuerpo empieza a deslizar y cuando está deslizando Fk, completando la siguiente tabla
| N=mg (N) | Fs (N) | Fk (N) |
|---|---|---|
| (96+1·250)·9.8/1000=3.39 | 1.40 | 1.12 |
| (96+2·250)·9.8/1000=5.84 | 2.50 | 2.04 |
| (96+3·250)·9.8/1000=8.29 | 3.70 | 3.15 |
| (96+4·250)·9.8/1000=10.74 | 4.40 | 4.00 |
| (96+5·250)·9.8/1000=13.19 | 5.60 | 4.93 |
En el eje X ponemos los datos de la reacción N y en el eje Y los datos de Fs. Trazamos la recta que mejor ajusta, Fr=μs·N, la pendiente es el coeficiente estático μs
N=[3.39,5.84,8.29,10.74,13.19];
Fs=[1.4,2.5,3.7,4.4,5.6];
plot(N,Fs,'ro','markersize',4,'markerfacecolor','r')
xlabel('N(N)')
ylabel('F_s(N)')
title('Coeficiente estático')
grid on
En el menú seleccionamos Tools/Basic Fitting, aparece un cuadro de diálogo donde marcamos la casilla linear en Plot fits. A continuación, pulsamos la flecha hacia la derecha --> para mostrar los coeficientes p1 y p2 del polinomio (recta) y=p1*x+p2 de ajuste.
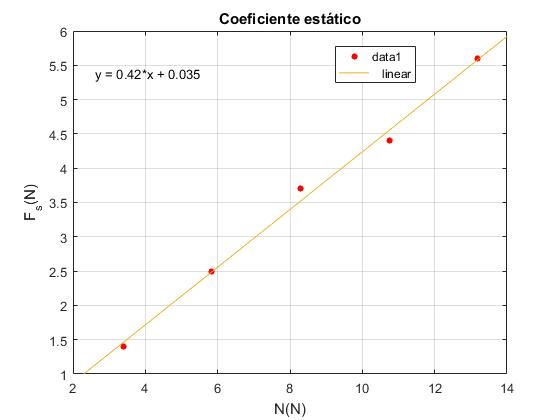
El coeficiente estático (pendiente de la recta) es el valor del coeficiente p1. El resultado es μs=0.42.
En el eje X ponemos los datos de la reacción N y en el eje Y los datos de Fk. Trazamos la recta que mejor ajusta, Fr=μk·N, la pendiente es el coeficiente cinético μk
N=[3.39,5.84,8.29,10.74,13.19];
Fk=[1.12,2.04,3.15,4,4.93];
plot(N,Fk,'ro','markersize',4,'markerfacecolor','r')
xlabel('N(N)')
ylabel('F_k(N)')
title('Coeficiente cinético')
grid on
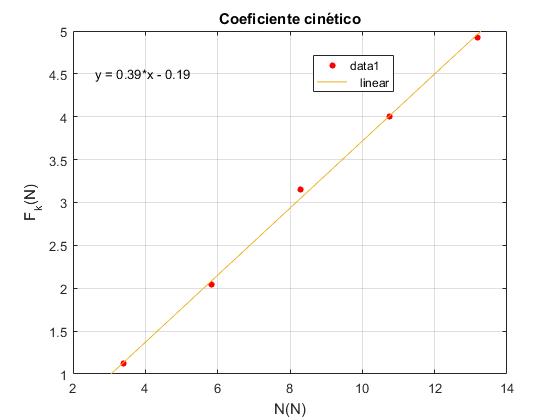
El coeficiente cinético (pendiente de la recta) es el valor del coeficiente p1. El resultado es μk=0.39.
Referencias
J. L. Meriam, L. G. Kraige. Engineering Mechanics, Volume 1, Statics. Seventh Edition, John Wiley & Sons, Inc. 2006, pp. 342-343
Subhranil De. Revisiting the Least Force Required to Keep a Block from Sliding. The Physics Teacher. Vol. 51, April 2013, pp. 220-221

