Principio de conservación de la energía

Si sobre una partícula actúa una fuerza conservativa, el trabajo de dicha fuerza es igual a la diferencia entre el valor inicial y final de la energía potencial

${\displaystyle \underset{A}{\overset{B}{{\displaystyle \int }}}\overrightarrow{F}·\overrightarrow{dr}=E_{pA}-E_{pB}}$

El trabajo de la resultante de las fuerzas que actúa sobre la partícula es igual a la diferencia entre el valor final e inicial de la energía cinética.

${\displaystyle \underset{A}{\overset{B}{{\displaystyle \int }}}\overrightarrow{F}·\overrightarrow{dr}=E_{kB}-E_{kA}}$

Igualando ambos trabajos, obtenemos la expresión del principio de conservación de la energía.

E_kA+E_pA=E_kB+E_pB

Se denomina energía mecánica a la suma de la energía cinética y potencial de la partícula.

Comprobación del principio de conservación de la energía

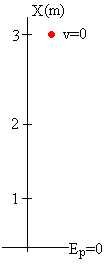
Un cuerpo de 2 kg se deja caer desde una altura de 3 m. Calcular

1. La velocidad del cuerpo cuando está a 1 m de altura y cuando llega al suelo, aplicando las fórmulas del movimiento rectilíneo uniformemente acelerado

2. La energía cinética potencial y total en dichas posiciones. Tomar g=10 m/s²

• Posición inicial x=3 m, v=0.

E_p=2·10·3=60 J, E_k=0, E_A=E_k+E_p=60 J

• Cuando x=1 m

${\displaystyle \begin{array}{l}1=3+\frac{1}{2}(-10)t^{2}t=\sqrt{2/5}\text{s}\\ v=-10·tv=\sqrt{40}\text{m/s}\end{array}}$

E_p=2·10·1=20 J, E_k=40, E_B=E_k+E_p=60 J

• Cuando x=0 m

${\displaystyle \begin{array}{l}0=3+\frac{1}{2}(-10)t^{2}t=\sqrt{3/5}\text{s}\\ v=-10·tv=\sqrt{60}\text{m/s}\end{array}}$

E_p=2·10·0=0 J, E_k=60, E_C=E_k+E_p=60 J

La energía total del cuerpo es constante. La energía potencial disminuye y la energía cinética aumenta.

Fuerzas no conservativas

Para darnos cuenta del significado de una fuerza no conservativa, vamos a compararla con la fuerza conservativa peso.

El peso es una fuerza conservativa.

Calculemos el trabajo de la fuerza peso cuando la partícula se traslada de A hacia B, y a continuación cuando se traslada de B hacia A.

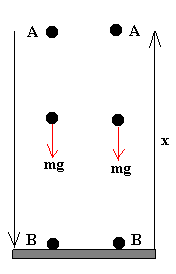
W_AB=mg x

W_BA=-mg x

El trabajo total a lo largo el camino cerrado A-B-A, W_ABA es cero.

La fuerza de rozamiento es una fuerza no conservativa

Cuando la partícula se mueve de A hacia B, o de B hacia A la fuerza de rozamiento es opuesta al movimiento, el trabajo es negativo por que la fuerza es de signo contrario al desplazamiento.

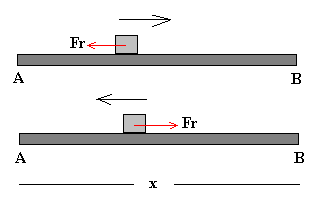
W_AB=-F_r x

W_BA=-F_r x

El trabajo total a lo largo del camino cerrado A-B-A, W_ABA es distinto de cero

W_ABA=-2F_r x

Balance de energía

En general, sobre una partícula actúan fuerzas conservativas $\overrightarrow{F_c}$ y no conservativas $\overrightarrow{F_{nc}}$ . El trabajo de la resultante de las fuerzas que actúan sobre la partícula es igual a la diferencia entre la energía cinética final menos la inicial.

${\displaystyle \underset{B}{\overset{A}{{{\displaystyle \int }}^{\text{}}}}\left(\overrightarrow{F_c}+\overrightarrow{F_{nc}}\right)\cdot \overrightarrow{dr}=E_{kB}-E_{kA}}$

El trabajo de las fuerzas conservativas es igual a la diferencia entre la energía potencial inicial y la final

${\displaystyle \underset{A}{\overset{B}{{\displaystyle \int }}}\overrightarrow{F_c}·\overrightarrow{dr}=E_{pA}-E_{pB}}$

Aplicando la propiedad distributiva del producto escalar obtenemos que

${\displaystyle \underset{B}{\overset{A}{{{\displaystyle \int }}^{\text{}}}}\overrightarrow{F_{nc}}\cdot \overrightarrow{dr}={\left(E_k+E_p\right)}_B-{\left(E_k+E_p\right)}_A=E_B-E_A}$

Ejemplo:

Un bloque de masa 0.2 kg inicia su movimiento hacia arriba, sobre un plano de 30º de inclinación, con una velocidad inicial de 12 m/s. Si el coeficiente de rozamiento entre el bloque y el plano es 0.16. Determinar:

• la longitud x que recorre el bloque a lo largo del plano hasta que se para

• la velocidad v que tendrá el bloque al regresar a la base del plano

Solución

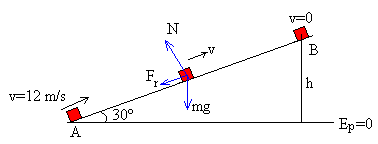
Cuando el cuerpo asciende por el plano inclinado

• La energía del cuerpo en A es E_A=½0.2·12²=14.4 J

• La energía del cuerpo en B es E_B=0.2·9.8·h=1.96·h =0.98·x J

• El trabajo de la fuerza de rozamiento cuando el cuerpo se desplaza de A a B es

W=-F_r·x=-μ·mg·cosθ·x=-0.16·0.2·9.8·cos30·x=-0.272·x J

De la ecuación del balance energético W=E_B-E_A, despejamos x=11.5 m, h=x·sin30º=5.75 m

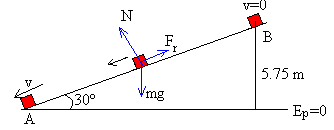
Cuando el cuerpo desciende

• La energía del cuerpo en B es E_B=0.2·9.8·h=1.96·h =0.98·x=0.98·11.5=11.28 J

• La energía del cuerpo en la base del plano E_A==½0.2·v²

• El trabajo de la fuerza de rozamiento cuando el cuerpo se desplaza de B a A es

W=-F_r·x=-μ·mg·cosθ·x=-0.16·0.2·9.8·cos30·11.5=-3.12 J

De la ecuación del balance energético W=E_A-E_B, despejamos v=9.03 m/s.