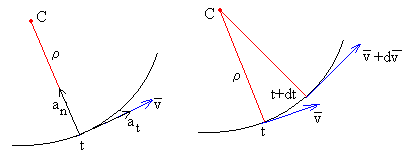
En la figura, se muestra el radio de curvatura y el centro de curvatura de una trayectoria cualesquiera en el instante t. Se dibuja la dirección del vector velocidad $\overrightarrow{v}$ en el instante t, la dirección del vector velocidad $\overrightarrow{v}+d\overrightarrow{v}$ en el instante t+dt. Se trazan rectas perpendiculares a ambas direcciones, que se encuentran en el punto C denominado centro de curvatura. La distancia ente entre la posición del móvil en el instante t, y el centro de curvatura C es el radio de curvatura ρ.

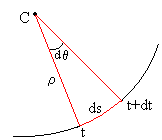
En el intervalo de tiempo comprendido entre t y t+dt, la dirección del vector velocidad cambia un ángulo dθ, que es el ángulo entre las tangentes o entre las normales. El móvil se desplaza en este intervalo de tiempo un arco ds=ρ·dθ,  tal como se aprecia en la figura.

Escribimos el vector velocidad$\overrightarrow{v}$ como producto de su módulo v por un vector unitario que tenga su misma dirección y sentido ${\widehat{u}}_t=\overrightarrow{v}/v$ . La derivada de un producto se compone de la suma de dos términos

${\displaystyle \overrightarrow{a}=\frac{d\overrightarrow{v}}{dt}=\frac{d(v{\widehat{u}}_t)}{dt}=\frac{dv}{dt}{\widehat{u}}_t+v\frac{d{\widehat{u}}_t}{dt}}$

El primer término, tiene la dirección de la velocidad o del vector unitario ${\widehat{u}}_t$, es la componente tangencial de la aceleración

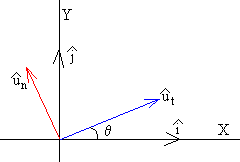
El segundo término, vamos a demostrar que tiene la dirección normal ${\widehat{u}}_n$. Como vemos en la figura las componentes del vector unitario ${\widehat{u}}_t$ son

${\displaystyle {\widehat{u}}_t=\cos \theta \widehat{i}+\sin \theta \widehat{j}}$

Su derivada es

${\displaystyle \frac{d{\widehat{u}}_t}{dt}=\left(-\sin \theta \widehat{i}+\cos \theta \widehat{j}\right)\frac{d\theta }{dt}=\frac{d\theta }{dt}{\widehat{u}}_n=\frac{1}{\rho }\frac{ds}{dt}{\widehat{u}}_n=\frac{v}{\rho }{\widehat{u}}_n}$

El vector aceleración es

${\displaystyle \overrightarrow{a}=\frac{d\overrightarrow{v}}{dt}=\frac{dv}{dt}{\widehat{u}}_t+\frac{v^2}{\rho }{\widehat{u}}_n}$

Las componentes tangencial y normal de la aceleración valen, respectivamente

${\displaystyle a_t=\frac{dv}{dt}{a}_n=\frac{v^2}{\rho }}$

Obtendremos esta última fórmula de una forma más simple para una partícula que describe un movimiento circular uniforme.

• Si solamente cambia el módulo de la velocidad con el tiempo, como en un movimiento rectilíneo, tenemos únicamente aceleración tangencial.

• Si solamente cambia la dirección de la velocidad con el tiempo, pero su módulo permanece constante como en un movimiento circular uniforme, tenemos únicamente aceleración normal.

• Si cambia el módulo y la dirección de la velocidad con el tiempo, como en un tiro parabólico, tendremos aceleración tangencial y aceleración normal.

Radio de curvatura

En el lenguaje ordinario, decimos que un trozo de carretera Δs tiene más curvatura que otro cuando el cambio de dirección Δθ es mayor a igualdad de camino recorrido en ambos. Compárese la figura de la izquierda con la de la derecha

El radio ρ de curvatura medio e instantáneo se definen, respectivamente,

${\displaystyle <\rho >=\frac{\Delta s}{\Delta \theta }\rho =\underset{\Delta s\to 0}{\lim }\frac{\Delta s}{\Delta \theta }=\frac{ds}{d\theta }}$

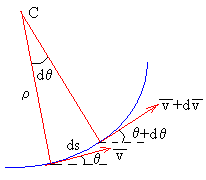
El radio de curvatura ρ y el centro C de curvatura se determinan del siguiente modo: Se traza la tangente a un punto de la trayectoria y a continuación, se traza la normal. Se toma un punto muy próximo al anterior, se traza la tangente y la normal en dicho punto.

Las normales se cortan en un punto denominado centro de curvatura C, y la distancia de C a uno u otro punto de la trayectoria, infinitamente próximos entre sí, se denomina radio de curvatura ρ.

Si el ángulo comprendido entre las dos tangentes es dθ, este es el ángulo que forman las dos normales. La longitud del arco entre los dos puntos considerados es ds=ρ·dθ .

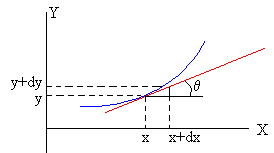
Dada la función y=f(x), vamos a determinar la fórmula que nos permite calcular el radio de curvatura ρ de la curva en la posición de abscisa x.

Como vemos en la figura, en el triángulo rectángulo de base dx, altura dy e hipotenusa ds, establecemos las siguientes relaciones

${\displaystyle \tan \theta =\frac{dy}{dx}ds=\sqrt{d{x}^2+d{y}^2}=\sqrt{1+{\left(\frac{dy}{dx}\right)}^2}dx}$

Despejamos el radio de curvatura es

${\displaystyle \rho =\frac{ds}{d\theta }=\frac{\sqrt{1+{\left(\frac{dy}{dx}\right)}^2}dx}{d\arctan \frac{dy}{dx}}=\frac{\sqrt{1+{\left(\frac{dy}{dx}\right)}^2}dx}{\frac{d^{2}y}{d{x}^2}dx/\left(1+{\left(\frac{dy}{dx}\right)}^2\right)}=\frac{{\left(1+{\left(\frac{dy}{dx}\right)}^2\right)}^{3/2}}{\frac{d^{2}y}{d{x}^2}}}$

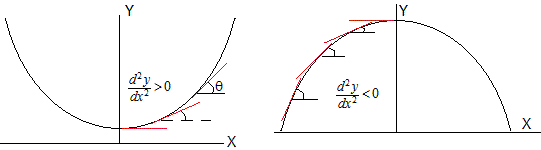
• En la figura de la izquierda, la pendiente tanθ=dy/dx crece, la derivada segunda es positiva
• En la figura de la derecha, la pendiente tanθ=dy/dx decrece, la derivada segunda es negativa

El radio de curvatura es una cantidad positiva

${\displaystyle \rho =\frac{{\left(1+{\left(\frac{dy}{dx}\right)}^2\right)}^{3/2}}{\left|\frac{d^{2}y}{d{x}^2}\right|}}$

Ejemplo

Al final de la página anterior hemos calculado las componentes tangencial y normal de la aceleración de un movimiento curvilíneo en el instante t=1.5 s. Conociendo la aceleración normal a_n=6.86 m/s² y el módulo de la velocidad v²=3²+5²=34, obtenemos el radio de curvatura

${\displaystyle \rho =\frac{v^2}{a_n}=\frac{34}{6.86}=4.96\text{m}}$

Vamos a calcular el radio ρ y el centro C de curvatura en el instante t=1.5 s o en la posición x₁=2.25 m, y₁=68.75 m

La ecuación de la trayectoria del movimiento curvilíneo y=f(x), la derivada primera dy/dx y la derivada segunda d²x/dx² son

${\displaystyle \begin{array}{l}y=50+20\sqrt{x}-5x\\ \frac{dy}{dx}=\frac{10}{\sqrt{x}}-5\\ \frac{d^{2}y}{d{x}^2}=-\frac{5}{x\sqrt{x}}\end{array}}$

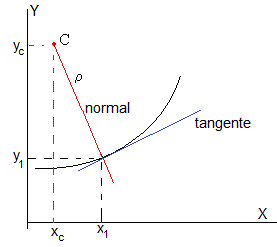
Calculamos sus valores en la posición x₁=2.25 m y las introducimos en la fórmula del radio de curvatura, obteniendo ρ=4.96 m

La derivada primera, nos da la pendiente m₁=1.67 de la recta tangente a la trayectoria en x₁=2.25 m. La pendiente de la recta normal m₂=-1/m₁=-0.6 (véase 'Rectas perpendiculares', al final de esta página)

La dirección normal contiene el punto (x₁, y₁) y al centro de curvatura de coordenadas (x_c, y_c), por tanto,

${\displaystyle y_c-y_1=m_2\left(x_c-x_1\right)}$

Por otra parte, la distancia entre el centro de curvatura (x_c, y_c) y el punto (x₁, y₁) es igual al radio de curvatura ρ

${\displaystyle {\rho }^2={\left(x_c-x_1\right)}^2+{\left(y_c-y_1\right)}^2}$

Despejamos x_c e y_c

${\displaystyle \begin{array}{l}{x}_c=x_1\pm \frac{\rho }{\sqrt{m_2^2+1}}\\ y_c=y_1+m_2\left(x_c-x_1\right)\end{array}}$

Las coordenadas del centro de curvatura son: x_c=6.50 m, y_c=66.20 m

Calculamos el radio y el centro de curvatura. Utilizamos la función diff de MATLAB para calcular la derivada primera y la derivada segunda de y respecto a x

syms x;
y=50+20*sqrt(x)-5*x;

%punto
x1=2.25;
y1=subs(y,x,x1);
r=(1+diff(y,1)^2)^(3/2)/diff(y,2);
rho=abs(subs(r,x,x1)); %radio curvatura
%centro curvatura
m2=-1/subs(diff(y,1),x,x1);
xc=x1+rho/sqrt(m2^2+1);
yc=y1+m2*(xc-x1);
disp('    xc,       yc,       r')
disp(double([xc,yc,rho]))

     xc,       yc,       r
    6.5000   66.2000    4.9563

Calculamos y representamos la función, el radio y centro de curvatura en el punto de abscisa x₁=2.25

f=@(x) 50+20*sqrt(x)-5*x;
hold on
fplot(f,[0,10])

%punto
x1=2.25;
y1=f(x1);
%radio de curvatura
r=(26*x1-100*sqrt(x1)+100)^(3/2)/5; %radio de curvatura
m2=-1/(10/sqrt(x1)-5); %pendiente de la recta normal
%centro de curvatura
xc=x1+r/sqrt(m2^2+1);
yc=y1+m2*(xc-x1);
line([xc,x1],[yc,y1],'Color','k');

%arco de circunferencia
ang=atan2((y1-yc),(x1-xc))*180/pi;
x2=zeros(0,90);
y2=zeros(0,90);
k=1;
for a=ang-45:ang+45
    x2(k)=xc+r*cosd(a);
    y2(k)=yc+r*sind(a);
    k=k+1;
end
plot(x2,y2,'r')
hold off
ylim([62,72]);
axis equal
grid on
xlabel('x')
ylabel('y')
title('Radio de curvatura')

>> r
r =    4.9563
>> m2
m2 =   -0.6000
>> xc
xc =    6.5000
>> yc
yc =   66.2000

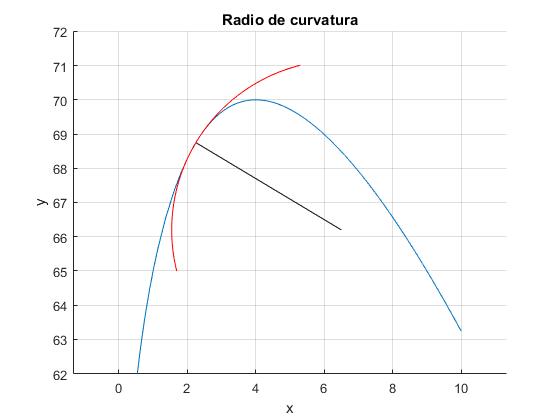
El segmento de color negro es el radio de curvatura ρ de la trayectoria seguida por el proyectil en el instante t=1.5 s, en el punto x₁=2.25 m, y₁=68.75 m, su extremo es el centro de curvatura de coordenadas x_c=6.50 m, y_c=66.20 m. En color rojo, el arco de circunferencia de radio ρ centrado en dicho punto

Rectas perpendiculares

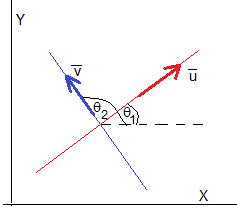
Consideremos dos rectas perpenduculares de pendientes m₁=tanθ₁ y m₂=tanθ₂. Trazamos un vector $\overrightarrow{u}$ entre dos puntos de la primera recta y un vector $\overrightarrow{v}$ en la segunda

${\displaystyle \begin{array}{l}\overrightarrow{u}=u\cos {\theta }_1\widehat{i}+u\sin {\theta }_1\widehat{j}\\ \overrightarrow{v}=v\cos {\theta }_2\widehat{i}+v\sin {\theta }_2\widehat{j}\end{array}}$

El producto escalar de dos vectores perpendiculares es cero y como consecuencia, la relación entre sus pendientes es m₁·m₂=-1

${\displaystyle \begin{array}{l}\overrightarrow{u}·\overrightarrow{v}=0\\ u\cos {\theta }_1·v\cos {\theta }_2+u\sin {\theta }_1·v\sin {\theta }_2=0\\ \frac{\sin {\theta }_1}{\cos {\theta }_1}=-\frac{\cos {\theta }_2}{\sin {\theta }_2}{m}_1=-\frac{1}{m_2}\end{array}}$

Referencia

Puig Adam P. Cálculo Integral Aplicado a la Física y Técnica. Biblioteca Matemática, 1972, pág. 286-287