Polinomios de Legendre

Ecuación diferencial	$(1 - x^{2}) \frac{d^{2} y}{d x^{2}} - 2 x \frac{d y}{d x} + n (n + 1) y = 0 n = 1,2,3...$
Fórmula de Rodríguez	$P_{n} (x) = \frac{1}{2^{n} n!} \frac{d^{n}}{d x^{n}} [{(x^{2} - 1)}^{n}]$
Relación de recurrencia	$(n + 1) P_{n + 1} (x) = (2 n + 1) x P_{n} (x) - n P_{n - 1} (x)$

Los primeros polinomios de Legendre son.

$\begin{array}{l} P_{0} (x) = 1 \\ P_{1} (x) = x \\ P_{2} (x) = \frac{1}{2} (3 x^{2} - 1) \\ P_{3} (x) = \frac{1}{2} (5 x^{3} - 3 x) \\ P_{4} (x) = \frac{1}{8} (35 x^{4} - 30 x^{2} + 3) \\ P_{5} (x) = \frac{1}{8} (63 x^{5} - 70 x^{3} + 15 x) \\ P_{6} (x) = \frac{1}{16} (231 x^{6} - 315 x^{4} + 105 x^{2} - 5) \\ P_{7} (x) = \frac{1}{16} (429 x^{7} - 693 x^{5} + 315 x^{3} - 35 x) \\ ..... \end{array}$

Utilizamos la función legendreP de MATLAB para mostrar los primeros polinomios de Legendre

>> syms x;
>> for n=1:7
   legendreP(n,x)
end

ans =x
ans =(3*x^2)/2 - 1/2
ans =(5*x^3)/2 - (3*x)/2
ans =(35*x^4)/8 - (15*x^2)/4 + 3/8
ans =(63*x^5)/8 - (35*x^3)/4 + (15*x)/8
ans =(231*x^6)/16 - (315*x^4)/16 + (105*x^2)/16 - 5/16
ans =(429*x^7)/16 - (693*x^5)/16 + (315*x^3)/16 - (35*x)/16

Mediante del comando diff de MATLAB, obtenemos la expresión de P₄(x) y P₅(x)

>> syms x;
>> n=4;
>> P4=diff((x^2-1)^n,n)/(2^n*factorial(n));
>> P4=simplify(P4)
P4 =(35*x^4)/8 - (15*x^2)/4 + 3/8
>> n=5;
>> P5=diff((x^2-1)^n,n)/(2^n*factorial(n));
>> P5=simplify(P5)
P5 =(x*(63*x^4 - 70*x^2 + 15))/8

Definimos la función legendre_p para obtener los coeficientes de los polinomios de Legendre, utilizando la relación de recurrencia

function p=legendre_p(n)
    p1=1;    
    p2=[1,0]; 
    if n==0
        p=p1; %P0
    elseif n==1
        p=p2; %P1
    else
        for i=2:n
            p=((2*(i-1)+1)*[p2,0]-(i-1)*[0,0,p1])/i;
            p1=p2;
            p2=p;
        end
    end
end

Generamos los polinomios de Legendre y comprobamos sus propiedades, etc. La función poly2sym convierte el vector de los coeficientes en un polinomio simbólico p(x).

>> syms x;
>> P4=poly2sym(legendre_p(4))
P4 =(35*x^4)/8 - (15*x^2)/4 + 3/8
>> P5=poly2sym(legendre_p(5))
P5 =(63*x^5)/8 - (35*x^3)/4 + (15*x)/8

Creamos la función recursiva legendre_r para obtener el valor de los polinomios cuando se proporciona el valor de x utilizando la relación de recurrencia, partiendo de P₀(x) =0 y P₁(x) =x

function res=legendre_r(n,x)
    if n==0
        res=ones(1,length(x));
    elseif n==1
        res=x;
    else       
        res=((2*(n-1)+1)*x.*legendre_r(n-1,x)-(n-1)*legendre_r(n-2,x))/n;
    end
end

Las llamadas a las funciones legendre_r y legendre_p, para calcular el valor del polinomio n=4 para x=0.5, P₄(0.5)

>> x=0.5;
>> legendre_r(4,x)
ans =   -0.2891
>> polyval(legendre_p(4),x)
ans =   -0.2891
>> legendreP(4,x)
ans =   -0.2891

producen los mismos resultados.

Representamos gráficamente los polinomios de P₁(x) a P₆(x) empleando el comando fplot. Utilizamos indistintamente las funciones legrendre_p que devuelve los coeficientes del polinomio en combinación con polyval, la función recursiva legendre_r o la función de MATLAB legendreP

hold on
for n=1:6
    %f=@(x) polyval(legendre_p(n),x);
    %f=@(x) legendre_r(n,x);
    f=@(x) legendreP(n,x);
    fplot(f,[-1,1]);
end
xlabel('x')
ylabel('P_n(x)')
title('Polinomios de Legendre')
grid on
hold off

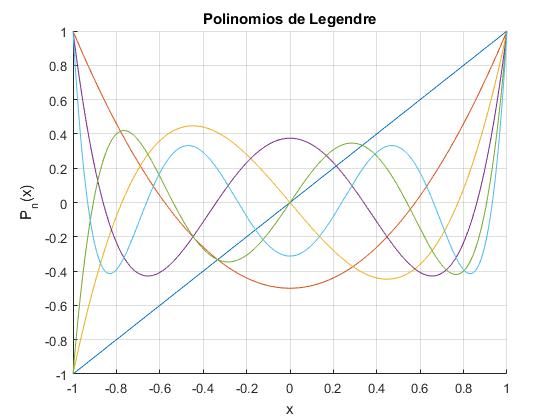
Propiedades

En la gráfica vemos que

P_n(1)=1

P_n(-1)=(-1)ⁿ

Si n es impar P_n(x)=-P_n(-x), de modo que P_n(0)=0

Comprobamos numéricamente mediante la función integral que el área bajo P_n(x) es nula, para n>1

$\int_{- 1}^{1} P_{n} (x) d x = 0, n \geq 1$

>> syms x;
>> for n=1:4
int(legendreP(n,x),x,-1,1)
end
 
ans =0
ans =0
ans =0
ans =0

Ortogonalidad

$\int_{- 1}^{1} P_{n} (x) P_{m} (x) d x = {\begin{cases} 0 m \neq n \\ \frac{2}{2 n + 1} m = n \end{cases}$

>> syms x;
>> int(legendreP(3,x)*legendreP(4,x),x,-1,1)
ans =0
>> int(legendreP(4,x)*legendreP(4,x),x,-1,1)
ans =2/9

Derivadas

$\begin{array}{l} \frac{d P_{n + 1} (x)}{d x} = (n + 1) P_{n} (x) + x \frac{d P_{n} (x)}{d x} \\ \frac{d P_{0} (x)}{d x} = 0, \frac{d P_{1} (x)}{d x} = 1, \frac{d P_{2} (x)}{d x} = 3 x,.... \end{array}$

>> syms x;
>> diff(legendreP(3,x))
ans =(15*x^2)/2 - 3/2
>> 3*legendreP(2,x)+x*diff(legendreP(2,x))
ans =(15*x^2)/2 - 3/2

Aproximación de una función mediante los polinomios de Legendre

Polinomio p(x) de grado N

$\begin{array}{l} 1 = P_{0} (x) \\ x = P_{1} (x) \\ x^{2} = \frac{1}{3} (2 P_{2} (x) + P_{0} (x)) \\ x^{3} = \frac{1}{5} (2 P_{3} (x) + 3 P_{1} (x)) \\ x^{4} = \frac{1}{35} (8 P_{4} (x) + 20 P_{2} (x) + 7 P_{0} (x)) \\ x^{5} = \frac{1}{63} (8 P_{5} (x) + 28 P_{3} (x) + 27 P_{1} (x)) \\ x^{6} = \frac{1}{231} (16 P_{6} (x) + 72 P_{4} (x) + 110 P_{2} (x) + 33 P_{0} (x)) \end{array}$

Un polinomio de grado N se puede expresar como una combinación lineal de N+1 polinomios de Legendre P_n(x), n=0, 1,2...N, utilizando las relaciones de ortogonalidad

$\begin{array}{l} f (x) = \sum_{n = 0}^{N} c_{n} P_{n} (x) \\ \int_{- 1}^{1} f (x) P_{m} (x) d x = \sum_{n = 0}^{N} c_{n} \int_{- 1}^{1} P_{n} (x) P_{m} (x) d x \\ \int_{- 1}^{1} f (x) P_{n} (x) d x = \frac{2}{2 n + 1} c_{n} \\ c_{n} = \frac{2 n + 1}{2} \int_{- 1}^{1} f (x) P_{n} (x) d x n = 0,1,2... N \end{array}$

Por ejemplo, P₂(x) es una función simétrica y f(x)=x³ es una función antisimétrica, entonces

$\int_{- 1}^{1} x^{3} P_{2} (x) d x = 0$

Por ejemplo, P₃(x) es una función antisimétrica y f(x)=x² es una función simétrica, entonces

$\int_{- 1}^{1} x^{2} P_{3} (x) d x = 0$

x³ es una combinación de polinomios de Legendre de índice impar y x² es una combinación de polinomios de Legendre de índice par

Sea el polinomio, f(x)=8x⁴-8x²+1=c₀P₀(x)+c₁P₁(x)+c₂P₂(x)+c₃P₃(x)+c₄P₄(x)

Elaboramos un script para calcular los coeficientes c₀, c₁, c₂, c₃ y c₄

syms x;
p=[8,0,-8,0,1]; %coeficientes del polinomio
pol=poly2sym(p); %polinomio
for n=0:length(p)-1
    P=poly2sym(legendre_p(n));
    c=(2*n+1)*int(pol*P,x,-1,1)/2; %coeficientes
    disp([n,c])
end

[ 0, -1/15]
[ 1, 0]
[ 2, -16/21]
[ 3, 0]
[ 4, 64/35]

$8 x^{4} - 8 x^{2} + 1 = \frac{64}{35} P_{4} (x) - \frac{16}{21} P_{2} (x) - \frac{1}{15} P_{0} (x)$

Comprobación

>> 64*poly2sym(legendre_p(4))/35-16*poly2sym(legendre_p(2))/21-1/15
ans =8*x^4 - 8*x^2 + 1

Utilizando la función legendreP de MATLAB obtenemos los mismos resultados

syms x;
p=[8,0,-8,0,1]; %coeficientes del polinomio
pol=poly2sym(p); %polinomio
for n=0:length(p)-1
    c=(2*n+1)*int(pol*legendreP(n,x),x,-1,1)/2; %coeficientes
    disp([n,c])
end

Comprobación

>> 64*legendreP(4,x)/35-16*legendreP(2,x)/21-1/15
 ans =8*x^4 - 8*x^2 + 1

Función f(x)

Aproximamos la función f(x) mediante la serie

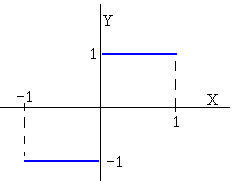
$\begin{array}{l} f (x) = \sum_{n = 0}^{\infty} c_{n} P_{n} (x) \\ c_{n} = \frac{2 n + 1}{2} \int_{- 1}^{1} f (x) P_{n} (x) d x \end{array}$

Vamos a aproximar la función f(x)=sgn(x) (función signo de MATLAB) de la figura a la combinación lineal de los N+1 primeros polinomios de Legendre

Para calcular cada uno de los coeficientes c_n (n=0...N) utilizamos la función integral para calcular numéricamente la integral definida entre los límites -1 y 1.

sign es una función de MATLAB que devuelve el signo de x.

Primero, calculamos los coeficientes c_n y después, la aproximación a la función f(x)

$f (x) \approx \sum_{n = 0}^{N} c_{n} P_{n} (x)$

N=10;
c=zeros(1,N+1);
for n=0:N
    c(n+1)=integral(@(x)sign(x).*legendreP(n,x),-1,1)*(n+1/2);
end

x=-1:0.02:1;
y=zeros(1,length(x));
for n=0:N
    y=y+c(n+1)*legendreP(n,x);
end
hold on
line([-1,0],[-1,-1])
line([0,1],[1,1])
plot(x,y,'r')
hold off
xlabel('x')
ylabel('f(x)')
title('Aproximación mediante polinomios de Legendre')
grid on

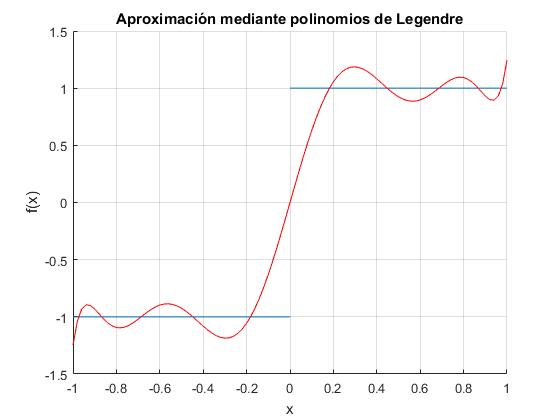
En color azul se dibuja la función f(x) y en color rojo la aproximación mediante la combinación lineal de los N+1=11 primeros polinomios de Legendre.

Energía potencial

Esta función de f(x) es importante en fisica, se desarrolla en serie de polinomios de Legendre

$\frac{1}{\sqrt{1 - 2 x t + t^{2}}} = \sum_{n = 0}^{\infty} P_{n} (x) t^{n}, | x | \leq 1, | t | < 1$

Comprobación. Tomamos t=0.6.

function legendre_3
    hold on
    t=0.6;
    f=@(x) 1./sqrt(1-2*x*t+t^2);
    fplot(f,[0,1])
     g=@(x) suma(10,x);
    fplot(g,[0,1])
    hold off
    grid on
    xlabel('x')
    ylabel('f(x)')
    title('funciones de Legendre')

    function s= suma(n,x)
        s=0;    
        for k=0:n
            s=s+legendreP(k,x)*t^k;
        end
    end
end

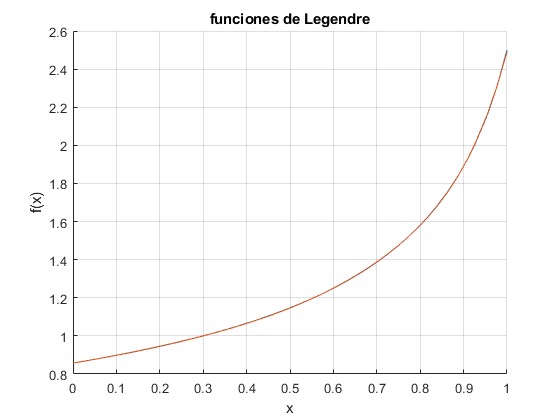
No se distingue la función f(x) del desarrollo en serie tomando únicamente 10 términos

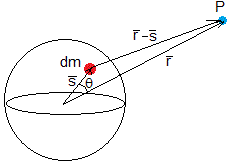
El potencial gravitatorio producido por un elemento diferencial de masa dm de un cuerpo (por ejemplo, la Tierra) en un punto P es inversamente proporcional a la distancia entre dm y P

$\begin{array}{l} \frac{1}{| \vec{r} - \vec{s} |} = \frac{1}{\sqrt{r^{2} + s^{2} - 2 s r \cos θ}} = \frac{1}{r} \frac{1}{\sqrt{\frac{s^{2}}{r^{2}} + 1 - 2 \frac{s}{r} \cos θ}}, {\begin{cases} x = \cos θ \\ t = \frac{s}{r} \end{cases} \\ \frac{1}{| \vec{r} - \vec{s} |} = \frac{1}{r} {\sum_{n = 0}^{\infty} P_{n} (\cos θ) (\frac{s}{r})}^{n}, s < r \end{array}$

Polinomios asociados de Legendre

La ecuación diferencial y su solución, los polinomios asociados de Legendre, son

$\begin{array}{l} (1 - x^{2}) \frac{d^{2} y}{d x^{2}} - 2 x \frac{d y}{d x} + (n (n + 1) - \frac{m^{2}}{1 - x^{2}}) y = 0 \\ y = P_{n}^{m} (x) = {(1 - x^{2})}^{m / 2} \frac{d^{m}}{d x^{m}} P_{n} (x) \\ P_{n}^{m} (x) = 0, m > n \end{array}$

Los primeros polinomios asociados de Legendre son

$\begin{array}{l} P_{0}^{0} (x) = P_{0} (x) = 1 \\ P_{1}^{0} (x) = P_{1} (x) = x \\ P_{1}^{1} (x) = \sqrt{1 - x^{2}} \frac{d}{d x} P_{1} (x) = \sqrt{(1 - x^{2})} \\ P_{2}^{0} (x) = P_{2} (x) = \frac{1}{2} (3 x^{2} - 1) \\ P_{2}^{1} (x) = \sqrt{1 - x^{2}} \frac{d}{d x} P_{2} (x) = 3 x \sqrt{(1 - x^{2})} \\ P_{2}^{2} (x) = \sqrt{{(1 - x^{2})}^{2}} \frac{d^{2}}{d x^{2}} P_{2} (x) = 3 (1 - x^{2}) \\ P_{3}^{0} (x) = P_{3} (x) = \frac{1}{2} (5 x^{3} - 3 x) \\ P_{3}^{1} (x) = \sqrt{1 - x^{2}} \frac{d}{d x} P_{3} (x) = \frac{3}{2} (5 x^{2} - 1) \sqrt{(1 - x^{2})} \\ P_{3}^{2} (x) = \sqrt{{(1 - x^{2})}^{2}} \frac{d^{2}}{d x^{2}} P_{3} (x) = 15 x (1 - x^{2}) \\ P_{3}^{3} (x) = \sqrt{{(1 - x^{2})}^{3}} \frac{d^{3}}{d x^{3}} P_{3} (x) = 15 {(1 - x^{2})}^{3 / 2} \end{array}$

syms x;
for n=0:4
    for m=0:n
        y=(1-x^2)^(m/2)*diff(legendreP(n,x),m);
        disp([n,m])
        y=simplify(y)
    end
end

     0     0    y =1
     1     0    y =x
     1     1    y =(1 - x^2)^(1/2)
     2     0    y =(3*x^2)/2 - 1/2
     2     1    y =3*x*(1 - x^2)^(1/2)
     2     2    y =3 - 3*x^2
     3     0    y =(x*(5*x^2 - 3))/2
     3     1    y =(1 - x^2)^(1/2)*((15*x^2)/2 - 3/2)
     3     2    y =-15*x*(x^2 - 1)
     3     3    y =15*(1 - x^2)^(3/2)
     4     0    y =(35*x^4)/8 - (15*x^2)/4 + 3/8
     4     1    y =(5*x*(1 - x^2)^(1/2)*(7*x^2 - 3))/2
     4     2    y =-(x^2 - 1)*((105*x^2)/2 - 15/2)
     4     3    y =105*x*(1 - x^2)^(3/2)
     4     4    y =105*(x^2 - 1)^2

Relaciones de ortogonalidad

$\begin{array}{l} \int_{- 1}^{1} P_{n}^{m} (x) P_{k}^{m} (x) d x = 0, n \neq k \\ \int_{- 1}^{1} {(P_{n}^{m} (x))}^{2} d x = \frac{2}{2 n + 1} \frac{(n + m)!}{(n - m)!} \end{array}$

Comprobamos la primera integral. Sea n=3, k=2 y m=2

>> syms x;
>> int(45*x*(1-x^2)^2,x,-1,1)
ans =0

Comprobamos la segunda integral. Sea n=3 y m=3

>> int(15^2*(1-x^2)^3,x,-1,1)
ans =1440/7
>> format rat
>> 2*factorial(6)/7
ans =    1440/7

Ejemplos en el curso de Física

La ecuación de Laplace, coordenadas esféricas

Esfera conductora y esfera dieléctrica en un campo eléctrico uniforme

La ecuación de Laplace, varilla y semiesfera cargada

La ecuación de Laplace, anillo y disco cargado

Vibraciones de una cuerda en rotación

Esfera iluminada por el Sol

La ecuación de Schrödinger en coordenadas esféricas (I)

Potencial de Morse y potencial de Pöschl–Teller

Efecto de la rotación de la Tierra en la aceleración de la gravedad

Referencias

Alan Jeffrey, Hui-Hui Dai. Handbook of Mathematical Formulas and Integrals. Elsevier (2008). págs. 310-313