La aceleración de la gravedad en el interior y en el exterior de una distribución esférica y uniforme de masa
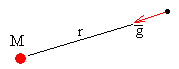
La aceleración de la gravedad en un punto P situado a una distancia r de la masa puntual M se define como la fuerza sobre la unidad de masa, situada en dicho punto. Es un vector de módulo
dirección radial y sentido hacia la masa puntual M, tal como se muestra en al figura.
El punto P está en el exterior de la esfera de radio R.
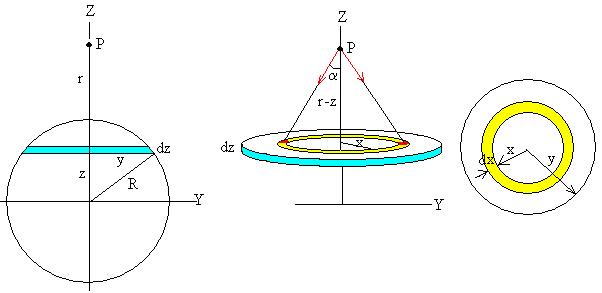
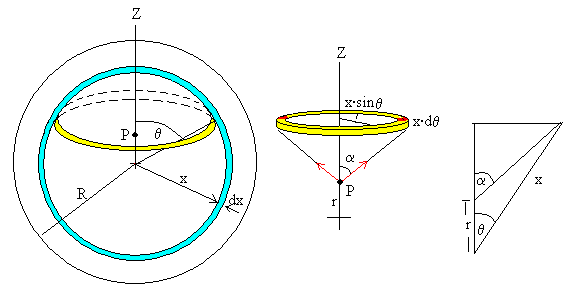
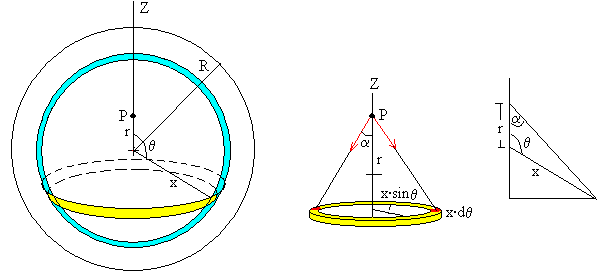
Supongamos que el punto P está situado a una distancia r>R a lo largo del eje Z del centro de un planeta de masa M. Dividimos la esfera en discos (de color azul claro) de radio y variable, de espesor dz, tal como se muestra en la figura. Para calcular la fuerza que ejerce uno de estos discos sobre la unidad de masa situada en P, dividimos cada disco en anillos (en color amarillo) de radio x, de anchura dx y espesor dz.
Por simetría, como vemos en la figura, las componentes horizontales (a lo largo del eje X e Y) de la fuerza que ejercen los elementos de masa del anillo (considerados como masas puntuales, en color rojo) se anulan de dos en dos, quedando solamente la componente Z de la fuerza resultante que ejerce la masa contenida en el anillo.
Si ρ es la densidad constante de la distribución esférica y uniforme de masa. La masa contenida en el anillo es ρ·(2πx·dx)·dz. La fuerza resultante que ejerce la masa contenida en el anillo sobre la sobre la unidad de masa situada en P es
Integramos respecto de la variable x, entre los límites 0 e y para calcular resultante de las fuerzas en P debidas a la distribución de masa contenida por el disco de radio y y de espesor dz.
Relacionamos la variable y y z para integrar respecto de la variable z entre los límites –R y +R
z2+y2=R2
La aceleración de la gravedad en el punto P, se obtendrá integrando
Integrando por partes el tercer término entre paréntesis
Alaternativa
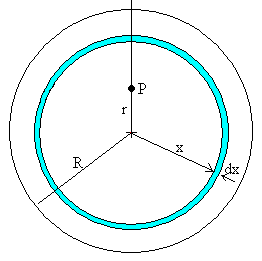
En vez de dividir la esfera en discos de radio variable y y espesor dz, dividimos la esfera en capas esféricas concéntricas de radio x y de espesor dx.
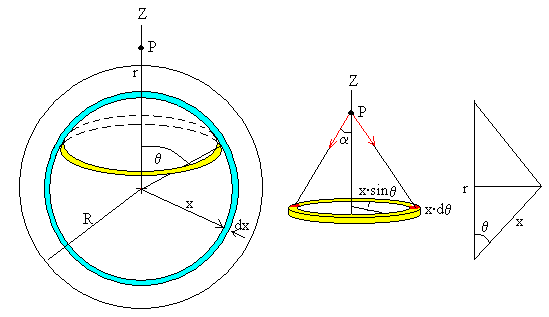
Dividimos dicha capa en anillos. Por simetría, como vemos en la figura, las componentes horizontales (a lo largo del eje X e Y) de la fuerza que ejercen los elementos de masa del anillo (considerados como masas puntuales, en color rojo) se anulan de dos en dos, quedando solamente la componente Z de la fuerza resultante que ejerce la masa contenida en el anillo.
Si ρ es la densidad constante de la distribución esférica y uniforme de masa. La masa contenida en el anillo es ρ·(2πxsinθ)·(x·dθ)·dx. La fuerza resultante que ejerce la masa contenida en el anillo sobre la sobre la unidad de masa situada en P
Integramos respecto de la variable θ, entre los límites 0 y π para calcular la fuerza sobre la unidad de masa situada en P ejercida por la distribución de masa contenida en la capa esférica de radio x y d espesor dx.
La primera integral es inmediata, integramos por partes la segunda. El resultado es
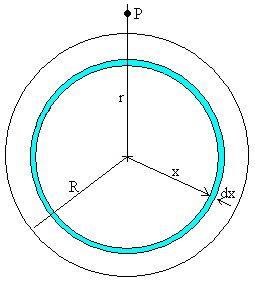
Esta expresión nos da la aceleración de la gravedad producida por una capa esférica de radio x y de espesor dx en un punto P situado a una distancia r>x del centro de la capa esférica.
Calculamos la fuerza ejercida por la esfera de masa M sobre la unidad de masa situada en P, sumando la fuerza que ejerce cada una de las capas esféricas en la que hemos dividido la esfera. El módulo de la aceleración de la gravedad vale.
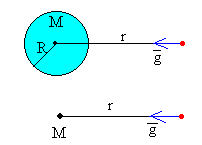
Si tenemos en cuenta que el vector apunta hacia el centro de la Tierra
El punto P está en el interior de la esfera de radio R.
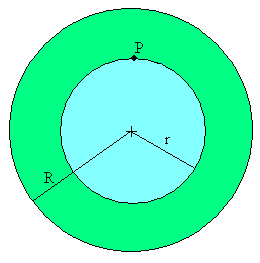
El punto P está a una distancia r<R del centro de la esfera. Dividimos la esfera en dos, una esfera hueca de radio interior r y radio exterior R. y una esfera maciza de radio r.
Fuerza que ejerce la esfera interior
La fuerza que ejerce la distribución de masa contenida en la esfera maciza de radio r sobre la unidad de masa situada en el punto P a una distancia r del centro, la hemos calculado en el apartado anterior, solamente hemos de cambiar el límite superior de la integral R por r.
Fuerza que ejerce la esfera exterior
Volvemos a calcular la fuerza que ejerce una capa esférica de radio r<x<R y de espesor dx, sobre la unidad de masa situada en P. Ahora bien, la fuerza en P debida a la masa contenida en los anillos que está por encima de P tiene la dirección del eje Z y sentido positivo, mientras que la fuerza en P debida a los anillos que están por debajo de P tiene la misma dirección pero sentido contrario.
Porción de la capa esférica por encima de P
Si ρ es la densidad constante de la distribución esférica y uniforme de masa. La masa contenida en el anillo es ρ·(2πxsinθ)·(x·dθ)·dx. La fuerza resultante que ejerce la masa contenida en el anillo sobre la sobre la unidad de masa situada en P
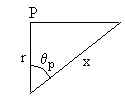
Integramos respecto de la variable θ, entre los límites 0 y θp=arccos(r/x) para calcular la fuerza sobre la unidad de masa situada en P ejercida por la porción de capa esférica de radio x y de espesor dx que está por encima de P.
La segunda integral es inmediata, integramos la primera por partes. El resultado es
Porción de la capa esférica por debajo de P
Si ρ es la densidad constante de la distribución esférica y uniforme de masa. La masa contenida en el anillo es ρ·(2πxsinθ)·(x·dθ)·dx. La fuerza resultante que ejerce la masa contenida en el anillo sobre la sobre la unidad de masa situada en P
Integramos respecto de la variable θ, entre los límites θp=arccos(r/x) y π para calcular la fuerza sobre la unidad de masa situada en P ejercida por la distribución de masa contenida en la capa esférica de radio x y de espesor dx.
La primera integral es inmediata, integramos la segunda por partes. El resultado es
Como la fuerza ejercida en P por la distribución de masa contenida en la capa semiesférica que está por encima de P y la fuerza ejercida en P por la distribución de masa contenida en por la parte de la capa semiesférica que está por debajo de P tienen el mismo valor pero signos contrarios. La fuerza neta en P debida a la capa semiesférica completa de radio x y de espesor dx es cero.
Fuerza total
Por tanto, la fuerza ejercida sobre la unidad de masa situada en P por la distribución de masa contenida en la esfera hueca de radio interior r y exterior R es cero.
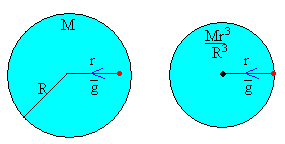
La fuerza ejercida sobre la unidad de masa situada en P a una distancia r del centro de la esfera de radio R, solamente es debida a la distribución de masa contenida en la esfera maciza de radio r<R
Si tenemos en cuenta que el vector apunta hacia el centro de la Tierra
r<R
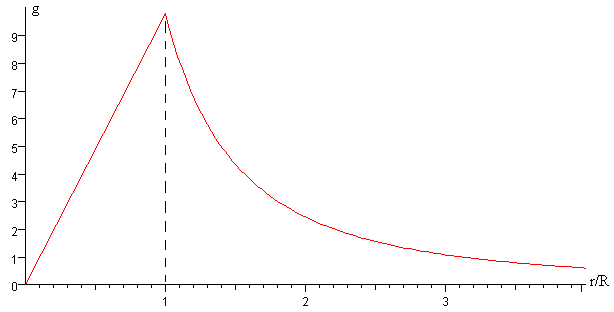
La aceleración de la gravedad g aumenta linealmente de 0 a GM/R2, en el interior de una distribución esférica y uniforme de masa M y radio R. En el exterior de dicha distribución, la aceleración de la gravedad disminuye en proporción inversa al cuadrado de la distancia al centro de dicha distribución GM/r2
En la figura, se muestra la gráfica del módulo de la aceleración de la gravedad g en función del cociente r/R para el planeta Tierra, G=6.67·10-11 Nm2/kg2, R=6.37·106 m, M=5.98·1024 kg. La aceleración de la gravedad en la superficie de la Tierra vale g=9.83 m/s2
Energía potencial
Una partícula de masa m experimenta una fuerza F=mg. La energía potencial Ep(r) correspondiente a esta fuerza conservativa se calcula del siguiente modo
Tomamos como nivel cero de energía potencial Ep(∞)=0
-
Energía potencial de la partícula para r>R
-
Energía potencial de la partícula para r<R
Para r>R, la expresión de la fuerza sobre la partícula es F(r)=-GMm/r2
Para r<R, la expresión de la fuerza sobre la partícula es F(r)=-GMmr/R3
En la figura, se representa la energía potencial Ep(r) en función del cociente (r/R)
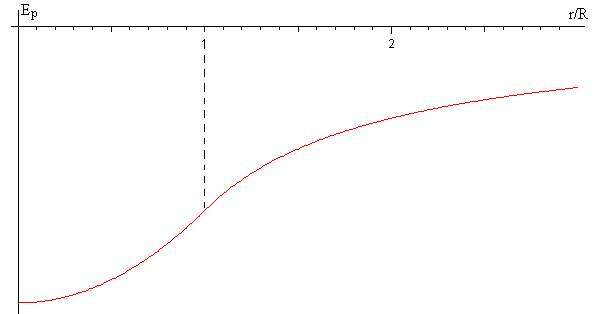
El principio de conservación de la energía
Conocida la posición r0 inicial y la velocidad inicial v0 de la partícula, calculamos la velocidad v de la partícula para una determinada posición r.
Sistema Tierra-Luna
Un ejercicio habitual en Física es el cálculo de la posición P, en la línea que une los centros de la Tierra y la Luna, donde las fuerzas de atracción de ambos cuerpos se cancelan.
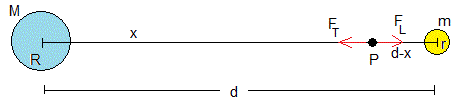
Supongamos que la Tierra es un cuerpo esférico de masa M y radio R y la Luna es un cuerpo esférico de masa m y radio r. Sea d la separación de los centros de ambos cuerpos.
La fuerza de atracción que ejerce la Tierra sobe un cuerpo de masa unidad situado en P es
La fuerza de atracción que ejerce la Luna sobre un cuerpo de masa unidad situado en P es
Ambas fuerzas tienen la misma dirección y sentido contrario, sus módulos son iguales en la posición P distante R≤x≤d-r del centro de la Tierra
Como el término d-x es positivo, extremos la raíz cuadrada y despejamos x
Con los datos de la Tierra y la Luna:
- Masa de la Tierra, M=5.98·1024 kg
- Radio de la Tierra, R=6 374 km
- Masa de la Luna, m=7.349·1022 kg
- Radio de la Luna, r=1 737 km
- Distancia media entre la Tierra y la Luna, d=384 000 km (60.2·R radios terrestres)
El resultado es xe=346 000 km o bien 54.2·R radios terrestres. Un posición cercana a la Luna debido a su menor masa
El campo gravitatorio de la Tierra se describe mediante la función
El campo gravitatorio de la Luna se describe mediante la función
En la línea que une los centros de la Tierra y la Luna, los campos tienen la misma dirección y sentido contrario.
Sabiendo que el gravitatorio en la superficie de la Tierra, suponiendo la Tierra un cuerpo aislado, es g=GM/R2
Para poder ver mejor la representación gráfica, se ha multiplicado la masa de la Luna por 5 y los radios de la Tierra y la Luna por 10.
G=6.67e-11; %constante G
R=10*6374; %radio de la Tierra
M=5.98e24; %masa de la Tierra
r=10*1737; %radio de la Luna
m=5*7.349e22; %masa de la Luna
d=384000; %distancia entre el centro de la Tierra y el centro de la Luna
g=G*M/(1000*R)^2; %aceleración de la gravedad en la Tierra
gM=@(x) g*((x>=R).*(R./x).^2+(x<R).*x/R);
gm=@(x) g*((m/M)*(x<=d-r).*(R./(d-x)).^2+(m/M)*(R/r)^2*(d-r<x).*((d-x)/r));
hold on
fplot(gM,[0,d])
fplot(gm,[0,d])
hold off
grid on
xlabel('x (km)')
ylabel('g (m/s^2)')
title('Aceleración de la gravedad Tierra-Luna')
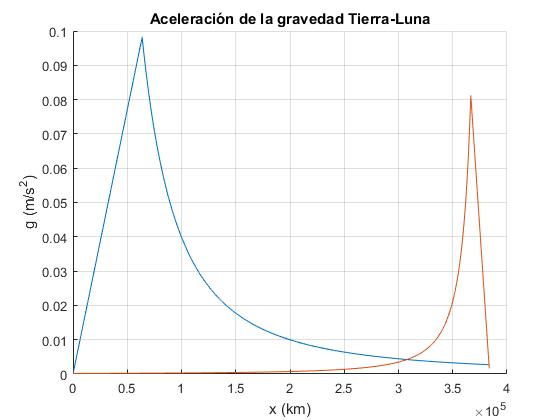
Además del punto que hemos calculado, situado entre la superficie de la Tierra y la superficie de la Luna xe=346 000 km, hay otros dos puntos situados uno en el interior de la Tierra y otro en el interior de la Luna.
El primer punto x<R se obtiene igualando el campo producido por la Luna en los puntos exteriores con el campo producido por la Tierra en sus puntos interiores
El segundo punto x>d-r se obtiene igualando el campo producido por la Tierra en los puntos exteriores con el campo producido por la Luna en sus puntos interiores
Resolvemos las ecuaciones cúbicas
G=6.67e-11; %constante G R=6374; %radio de la Tierra M=5.98e24; %masa de la Tierra r=1737; %radio de la Luna m=7.349e22; %masa de la Luna d=384000; %distancia entre el centro de la Tierra y el centro de la Luna x1=raices_3([1,-2*d/R,(d/R)^2,-m/M]) x2=raices_3([1,-d/r,0,M/m])
Hemos utilizado la función raices_3 definida en la página titulada Raíces de una ecuación (I)
>> format long x1 = 0.000003386014249 60.259025071776179 60.230460089432654 x2 = 1.0e+02 * -0.006058658395533 2.210691467350754 0.006075308488648 >> x1(1)*R*1000 ans = 21.582454825860964 >> d-x2(2)*r ans = 2.892121174081694
- El primer punto está situado a 21.58 m del centro de la Tierra
- El segundo punto está situado a 2.89 km del centro de la Luna
- El tercer punto, que calculamos al principio de este apartado, a una distancia 346 000 km, del centro de la Tierra
Aceleración de la gravedad en el polo
El cálculo de la aceleración de la gravedad en el polo producido por una distribución uniforme de masa en forma de esferoide de revolución de semiejes a y b, es un interesante ejercicio de cálculo integral, continuación del efectuado en el apartado La gravedad en el exterior de una distribución esférica y uniforme de masa
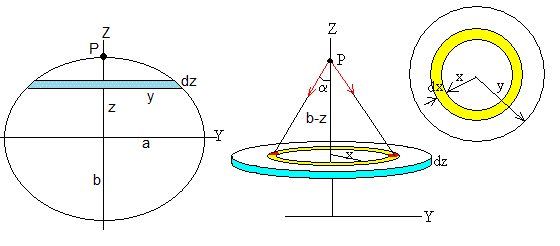
Supongamos que el punto P está en el polo Norte a lo largo del eje Z distante b del centro de la Tierra. Dividimos el elipsoide de revolución en discos (de color azul claro) de radio y variable y de espesor dz, tal como se muestra en la figura. Para calcular la fuerza que ejerce uno de estos discos sobre la unidad de masa situada en P, dividimos cada disco en anillos (en color amarillo) de radio x, de anchura dx y espesor dz.
Por simetría, como vemos en la figura, las componentes horizontales (a lo largo del eje X e Y) de la fuerza que ejercen los elementos de masa del anillo (considerados como masas puntuales, en color rojo) se anulan de dos en dos, quedando solamente la componente Z de la fuerza resultante que ejerce la masa contenida en el anillo.
Si ρ es la densidad constante y uniforme de masa. La masa contenida en el anillo es ρ(2πx·dx)dz. La fuerza resultante que ejerce la masa contenida en el anillo sobre la sobre la unidad de masa situada en P es
Integramos respecto de la variable x, entre los límites 0 e y para calcular resultante de las fuerzas en P debidas a la distribución de masa contenida en el disco de radio y y de espesor dz.
La integral es inmediata haciendo el cambio u=x2+(b-z)2, du=2x·dx
Relacionamos la variable y y z para integrar respecto de la variable z entre los límites –b y +b. Para un elipsoide de revolución de semiejes a y b
La aceleración de la gravedad g en el punto P, se obtendrá integrando
La integral de la derecha requiere más trabajo, se hace el cambio de variable
Se hace el cambio de variable, u=tant, du=dt/cos2(2t)
Teniendo en cuenta las relaciones trigonométricas
Deshacemos los cambios de variable
Evaluamos el integrando entre el límite superior b e inferior -b
La aceleración de la gravedad g en el punto P, es
Consideremos un elipsoide de revolución de la misma masa M y con el mismo volumen que una esfera de radio R, a2b=R3 (más abajo, se deduce la fórmula del volumen de un elipsoide de revolución). Llamamos
La aceleración de la gravedad g en el polo es
Calculamos el cociente g/g0 para la Tierra, f=3.35·10-3
>> syms f; >> y=3*(1-f)^(2/3)*(1+(1-f)*((1-f)*sqrt(f*(2-f))-atan(sqrt(f*(2-f))/(1-f))) /(f*(2-f))^(3/2)); >> yy=subs(y,f,3.35e-3); >> vpa(yy,10) ans =1.000445199
Como el parámetro f=(a-b)/a es muy pequeño, hacemos un desarrollo en serie
>> taylor(y,f) ans =(2*f)/15 - (41*f^2)/315 - (100*f^3)/567 - (2909*f^4)/18711 + 1
Los primeros términos del desarrollo en serie son
La aceleración de la gravedad en el polo de un cuerpo en forma de elipsoide de revolución es un poco mayor que la aceleración gravedad que correspondería a una distribución esférica y uniforme de masa
Volumen de un elipsoide de revolución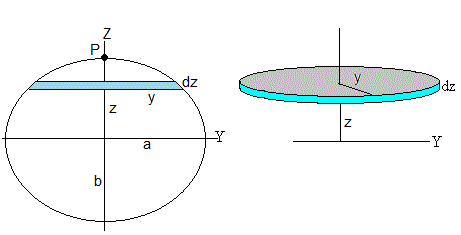
Dividimos el elipsoide en discos de radio y y de espesor dz. El volumen de cada uno de los discos es πy2dz, el volumen total es
Referencias
F M S Lima. Where else is null the gravitational field between two massive spheres?. Eur. J. Phys. 30 (2009) pp. 785-792

