Aproximación de funciones

De modo análogo a las series de Fourier, expresemos la función f(x) definida en el intervalo [-1,1] como combinación lineal de m polinomios T_j(x)

${\displaystyle f(x)\approx \frac{c_0}{2}+{\displaystyle \sum _{j=1}^m{c}_j{T}_j(x)}}$

Como hemos visto, las raíces del polinomio de grado n, T_n(x) son

${\displaystyle x_k=\cos \left(\frac{(2k-1)\pi }{2n}\right)k=\mathrm{1,2....}n}$

Sea m<n. Expresamos

${\displaystyle f(x_k)=\frac{c_0}{2}+{\displaystyle \sum _{j=1}^m{c}_j{T}_j(x_k)}}$

Empleando las relaciones de ortogonalidad, calculamos los valores de los coeficientes c_j, de un modo similar a las series de Fourier.

${\displaystyle \begin{array}{l}{\displaystyle \sum _{k=1}^{n}f(x_k)T_i(x_k)}=\frac{c_0}{2}{\displaystyle \sum _{k=1}^n{T}_i(x_k)}+{\displaystyle \sum _{j=1}^m{c}_j\left({\displaystyle \sum _{k=1}^n{T}_j(x_k)T_i(x_k)}\right)}\\ {\displaystyle \sum _{k=1}^{n}f(x_k)T_i(x_k)}=c_i\frac{n}{2}\\ c_i=\frac{2}{n}{\displaystyle \sum _{k=1}^{n}f(x_k)T_i(x_k)}\end{array}}$

Cuando i=0, T₀(x)=1

${\displaystyle \begin{array}{l}{\displaystyle \sum _{k=1}^{n}f(x_k)=}\frac{c_0}{2}n\\ c_0=\frac{2}{n}{\displaystyle \sum _{k=1}^{n}f(x_k)}\end{array}}$

Teniendo en cuenta que T_j(x)=cos(jθ) y que x_k=cosθ_k, con θ_k=(2k-1)π/(2n)

${\displaystyle T_j(x_k)=\cos \left(\frac{j(2k-1)\pi }{2n}\right)}$

Los coeficientes c_j con j=1,...m, se calculan mediante la fórmula

${\displaystyle c_j=\frac{2}{n}{\displaystyle \sum _{k=1}^{n}f\left(\cos \left(\frac{(2k-1)\pi }{2n}\right)\right)\cos \left(\frac{j(2k-1)\pi }{2n}\right)}}$

El código de la función chebfit que calcula los coeficientes c_j con j=0,...n-1, es el siguiente

function [c] = chebfit(n,f)
  y=cos((2*(1:n)-1)*pi/(2*n));  
  fk=f(y);
  c0=sum(fk)*2/n;
  ck=zeros(1,n-1);
  for j=1:n-1
    coseno=cos(j*(2*(1:n)-1)*pi/(2*n));
    ck(j)=sum(fk.*coseno)*2/n;
  end 
  c=[c0 ck];
end

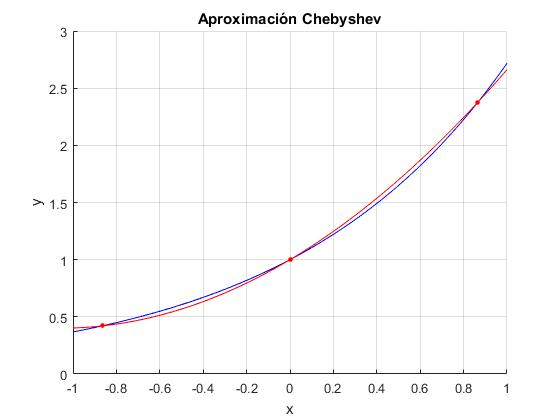
Como ejemplo, dibujamos la función f(x)=exp(x) en el intervalo de [-1,1] en color azul y aproximamos dicha función mediante polinomios de Chebyshev tomando n=3, en color rojo. Señalamos los puntos (nodos) las raíces del polinomio T_n(x).

f=@(x) exp(x);  %función
n=3; 
c=chebfit(n,f);
hold on
x=linspace(-1,1,100);
yy=zeros(length(x),1);
plot(x,f(x),'b') %dibuja la función en el intervalo [-1,1]
%aproximación a la función mediante polinomios de Chebyshev
yy=c(1)/2;
for j=2:n
    yy=yy+c(j)*polyval(chebypoly(j-1),x);
end
plot(x,yy,'r')
%puntos nodos
x=cos((2*(1:n)-1)*pi/(2*n));  
plot(x,f(x),'ro','markersize',4,'markerfacecolor','r')
hold off
grid on
xlabel('x')
ylabel('y')
title('Aproximación Chebyshev')

%utiliza Math Symbolic
cheb=c(1)/2;
for j=2:n
    cheb=cheb+c(j)*poly2sym(chebypoly(j-1));
end
vpa(cheb,6)

En la ventana de comandos observamos el polinomio aproximador, cuyos coeficientes se proporcionan con 6 cifras decimales

ans =0.532042*x^2 + 1.12977*x + 1.0

Cambiamos en la primera línea del script la definición de la función anónima f para estudiar el siguiente ejemplo.

${\displaystyle y=\frac{1}{1+25x^2}}$

El resultado con n=7 es el siguiente

f=@(x) 1./(1+25*x.^2);  %función
n=7; 
%... el resto igual

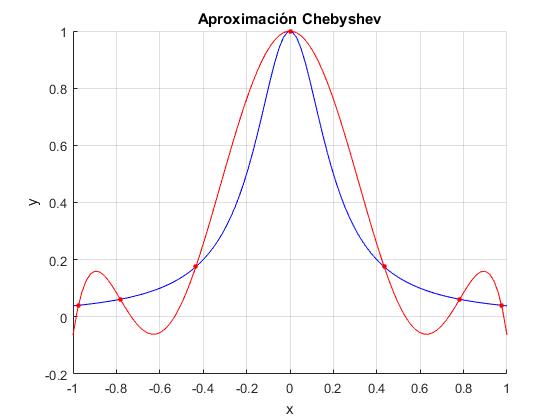
El polinomio aproximador aparece en la ventana de comandos. Se han suprimido los coeficientes próximos a cero

ans =- 6.79168*x^6 + 12.1571*x^4 - 6.429*x^2 + 1.0

Dibujamos este polinomio con la función ezplot en el intervalo [-1,1] y obtendremos la curva en color rojo.

Aproximación de funciones definidas en el intervalo [a,b]

Si la función f(x) está definida en el intevalo [a,b], en vez del intervalo [-1,1] hacemos el cambio de variable

${\displaystyle y=\frac{x-\frac{1}{2}(b+a)}{\frac{1}{2}(b-a)}}$

Cuando x varía de a a b, y varía de -1 a 1.

Modificamos la función chebfit y el script par incorporar esta posibilidad.

function [c] = chebfit_ab(a,b,n,f)
  y=cos((2*(1:n)-1)*pi/(2*n));  
  fk=f(y*(b-a)/2+(b+a)/2);
  c0=sum(fk)*2/n;
  ck=zeros(1,n-1);
  for j=1:n-1
    coseno=cos(j*(2*(1:n)-1)*pi/(2*n));
    ck(j)=sum(fk.*coseno)*2/n;
  end 
  c=[c0 ck];
end

Dibujamos la función

${\displaystyle y=\frac{\exp \left(-x^2/2\right)}{\sqrt{2\pi }}}$

en el intervalo de [-3,3] en color azul y aproximamos dicha función mediante polinomios de Chebyshev tomando n=5, en color rojo.

f=@(x) exp(-x.^2/2)/sqrt(2*pi);
n=5;
a=-3;
b=3;
c=chebfit_ab(a,b,n,f);
hold on
x=linspace(-1,1,100);
xx=(a+b)/2+(b-a)*x/2;
yy=zeros(length(x),1);
plot(xx,f(xx),'b')
yy=c(1)/2;
for j=2:n
    yy=yy+c(j)*polyval(chebypoly(j-1),x);
end
plot(xx,yy,'r')
%puntos nodos
x=cos((2*(1:n)-1)*pi/(2*n));  
xx=(a+b)/2+(b-a)*x/2;
plot(xx,f(xx),'ro','markersize',4,'markerfacecolor','r')
hold off
grid on
xlabel('x')
ylabel('y')
title('Aproximación Chebyshev')

syms x;
func=c(1)/2;
for j=2:n
    func=func+c(j)*poly2sym(chebypoly(j-1));
end
func=subs(func,x,(2*x-(a+b))/(b-a));
vpa(func,6)

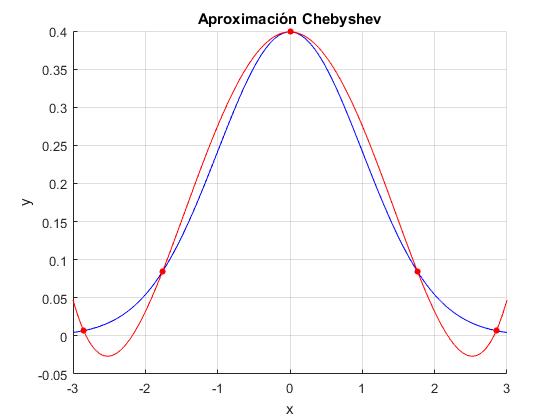
El polinomio aproximador aparece en la ventana de comandos. Se han suprimido los coeficientes próximos a cero

ans =0.0105398*x^4 - 0.13397*x^2 + 0.398942

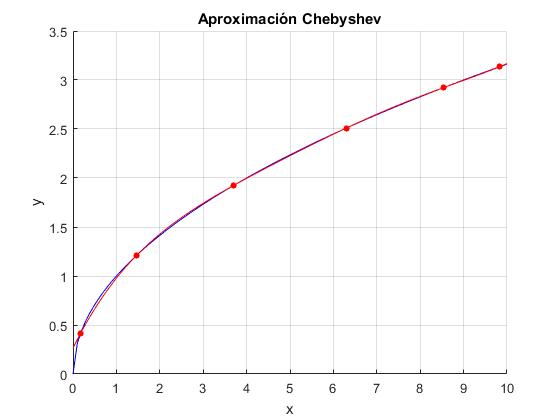
Dibujamos la función $y=\sqrt{x}$ en el intervalo de [0,10] en color azul y aproximamos dicha función mediante polinomios de Chebyshev tomando n=6, en color rojo.

f=@(x) sqrt(x);
n=6;
a=0;
b=10;
c=chebfit_ab(a,b,n,f);
......

ans =0.225068*x - 0.136044*(0.2*x - 1.0)^2 + 0.0141154*(0.2*x - 1.0)^3 
- 0.375426*(0.2*x - 1.0)^4 + 0.311013*(0.2*x - 1.0)^5 + 1.1024
>> vpa(expand(ans),6)
ans =0.0000995242*x^5 - 0.00308879*x^4 + 0.0370076*x^3 - 0.221643*x^2 + 
0.899309*x + 0.265797 

La línea final es el polinomio aproximador.

Series de polinomios de Chebyshev

Los primeros polinomios de Chebyshev son

T₀(x)=1
T₁(x)=x
T₂(x)=2x²-1
T₃(x)=4x³-3x
T₄(x)=8x⁴-8x²+1
T₅(x)=16x⁵-20x³+5x
T₆(x)= 32x⁶-48x⁴+18x²-1
....

Potencias de x

Escribimos las potencias de x, xⁿ en términos de los polinomios de Chebyshev

${\displaystyle \begin{array}{l}1=T_0\\ x=T_1\\ x^2=\frac{1}{2}\left(T_2+1\right)=\frac{1}{2}\left(T_2+T_0\right)\\ x^3=\frac{1}{4}\left(T_3+3x\right)=\frac{1}{4}\left(T_3+3T_1\right)\\ x^4=\frac{1}{8}\left(T_4+8x^2-1\right)=\frac{1}{8}\left(T_4+8\frac{1}{2}\left(T_2+T_0\right)-T_0\right)=\frac{1}{8}\left(T_4+4T_2+3T_0\right)\\ x^5=\frac{1}{16}\left(T_5+20x^3-5x\right)=\frac{1}{16}\left(T_5+20\frac{1}{4}\left(T_3+3T_1\right)-5T_1\right)=\frac{1}{16}\left(T_5+5T_3+10T_1\right)\\ \mathrm{....}\end{array}}$

Expresamos las potencias xⁿ en términos de los polinomios de Chebyshev T_n(x),T_n-2(x), T_n-4(x)..., teniendo en cuenta la relación existente entre cosⁿθ y cos(n-2)θ, cos(n-4)θ... y la simetría de los números combinatorios

${\displaystyle \left(\begin{array}{c}n\\ m\end{array}\right)=\left(\begin{array}{c}n\\ n-m\end{array}\right)}$

>> nchoosek(7,3)
ans =    35
>> nchoosek(7,4)
ans =    35

Supongamos que n=4, un número par

${\displaystyle \begin{array}{l}{\left(e^{i\theta }+e^{-i\theta }\right)}^4=e^{i4\theta }+\left(\begin{array}{c}4\\ 1\end{array}\right)e^{i3\theta }{e}^{-i\theta }+\left(\begin{array}{c}4\\ 2\end{array}\right)e^{i2\theta }{e}^{-i2\theta }+\left(\begin{array}{c}4\\ 3\end{array}\right)e^{i\theta }{e}^{-i3\theta }+e^{-i4\theta }\\ {\left(e^{i\theta }+e^{-i\theta }\right)}^4=\left(e^{i4\theta }-e^{-i4\theta }\right)+\left(\begin{array}{c}4\\ 1\end{array}\right)\left(e^{i2\theta }-e^{-i2\theta }\right)+\left(\begin{array}{c}4\\ 2\end{array}\right)\\ 2^4{\left(\cos \theta \right)}^4=2\cos \left(4\theta \right)+2\left(\begin{array}{c}4\\ 1\end{array}\right)\cos \left(2\theta \right)+\left(\begin{array}{c}4\\ 2\end{array}\right)\\ {\left(\cos \theta \right)}^4=\frac{1}{2^3}\left(\cos \left(4\theta \right)+\left(\begin{array}{c}4\\ 1\end{array}\right)\cos \left(2\theta \right)+\frac{1}{2}\left(\begin{array}{c}4\\ 2\end{array}\right)\right)\\ x^4=\frac{1}{2^3}\left(T_4+4T_2+3T_0\right)\end{array}}$

Supongamos que n=5, un número impar

${\displaystyle \begin{array}{l}{\left(e^{i\theta }+e^{-i\theta }\right)}^5=e^{i5\theta }+\left(\begin{array}{c}5\\ 1\end{array}\right)e^{i4\theta }{e}^{-i\theta }+\left(\begin{array}{c}5\\ 2\end{array}\right)e^{i3\theta }{e}^{-i2\theta }+\left(\begin{array}{c}5\\ 3\end{array}\right)e^{i2\theta }{e}^{-i3\theta }+\\ \left(\begin{array}{c}5\\ 4\end{array}\right)e^{i\theta }{e}^{-i4\theta }+e^{-i5\theta }\\ {\left(e^{i\theta }+e^{-i\theta }\right)}^5=\left(e^{i5\theta }-e^{-i5\theta }\right)+\left(\begin{array}{c}5\\ 1\end{array}\right)\left(e^{i3\theta }-e^{-i3\theta }\right)+\left(\begin{array}{c}5\\ 2\end{array}\right)\left(e^{i\theta }-e^{-i\theta }\right)\\ 2^5{\left(\cos \theta \right)}^5=2\cos \left(5\theta \right)+2\left(\begin{array}{c}5\\ 1\end{array}\right)\cos \left(3\theta \right)+\left(\begin{array}{c}5\\ 2\end{array}\right)\cos \left(\theta \right)\\ {\left(\cos \theta \right)}^5=\frac{1}{2^4}\left(\cos \left(5\theta \right)+\left(\begin{array}{c}5\\ 1\end{array}\right)\cos \left(3\theta \right)+\left(\begin{array}{c}5\\ 2\end{array}\right)\cos \left(\theta \right)\right)\\ x^5=\frac{1}{16}\left(T_5+5T_3+10T_1\right)\end{array}}$

Elaboramos una función, para obtener las potencias de x en términos de los polinomios de Chebyshev

function [T] = potencias_cheby(n)
    if rem(n,2)==0
        T=zeros(1,n);
        for k=0:n/2-1
            T(2*k+1)=nchoosek(n,k)/2^(n-1);
        end
        T0=nchoosek(n,n/2)/2^n;
        T=[T,T0];
    else
        T=zeros(1,n+1);
        for k=0:floor(n/2)
            T(2*k+1)=nchoosek(n,k)/2^(n-1);
        end
    end
end

Calculamos las potencias xⁿ=c₁T_n+c₂T_n-1+...+c_nT₁+c_n+1T₀

for k=0:6
    disp(['x^',num2str(k),'= ',num2str(potencias_cheby(k))])
end

x^0= 1
x^1= 1  0
x^2= 0.5           0         0.5
x^3= 0.25           0        0.75           0
x^4= 0.125           0         0.5           0       0.375
x^5= 0.0625           0      0.3125           0       0.625      0
x^6= 0.03125           0      0.1875           0     0.46875     0    0.3125

Desarrollo en serie en términos de los polinomios de Chebyshev

La fórmula del desarrollo en serie de Taylor es

${\displaystyle f(x)=f(a)+f^{\text{'}}(a)(x-a)+\frac{f^{\text{'}\text{'}}(a)}{2!}{(x-a)}^2+\mathrm{...}+\frac{f^{(n)}(a)}{n!}{(x-a)}^n+\mathrm{...}}$

El desarrollo en serie de log(x) cuando a=1 y tomando n=5 términos

>> syms x;
>> taylor(log(x),x,'ExpansionPoint',1,'Order',5)
ans =x - (x - 1)^2/2 + (x - 1)^3/3 - (x - 1)^4/4 - 1

En el caso particular de que a=0, se conoce como serie de Maclaurin. El desarrollo en serie de la función e^x, tomando n=7 términos, es

${\displaystyle e^x\approx 1+x+\frac{x^2}{2}+\frac{x^3}{6}+\frac{x^4}{24}+\frac{x^5}{120}+\frac{x^6}{720}+\mathrm{...}}$

>> syms x;
>> taylor(exp(x),'order',7)
ans =x^6/720 + x^5/120 + x^4/24 + x^3/6 + x^2/2 + x + 1

Sustituimos las potencias de x por combinaciones lineales de polinomios de Chebyshev

${\displaystyle \begin{array}{l}{e}^x\approx T_0+T_1+\frac{1}{2}·\frac{1}{2}\left(T_0+T_2\right)+\frac{1}{6}·\frac{1}{4}\left(3T_1+T_3\right)+\frac{1}{24}·\frac{1}{8}\left(3T_0+4T_2+T_4\right)+\\ \frac{1}{120}·\frac{1}{16}\left(10T_1+5T_3+T_5\right)+\frac{1}{720}·\frac{1}{32}\left(10T_0+15T_2+6T_4+T_6\right)=\\ c_1{T}_6+c_2{T}_5+c_3{T}_4+c_4{T}_3+c_5{T}_2+c_6{T}_1+c_7{T}_0\end{array}}$

Elaboramos un script para aproximar la función f(x)=e^x a un desarrollo en serie en términos de los polinomios de Chebyshev, calculando los coeficientes c₁, c₂...c₆ y c₇ que multiplican a los polinomios de Chebyshev, T₆, T₅...T₁ y T₀, respectivamente

syms x;
n=7; %número de términos
c_x=sym2poly(taylor(exp(x),'order',n));
cT=zeros(1,n);
for k=1:n
    a=[zeros(1,k-1),potencias_cheby(n-k)];
    cT=cT+c_x(k)*a;
end

Partimos de la suma c₁T₆+c₂T₅+c₃T₄+c₄T₃+c₅T₂+c₆T₁+c₇T₀. Escribimos cada polinomio T_i(x) en función de la variable x y comprobamos que obtenemos el desarrollo en serie de Taylor original de n=7 términos

syms x;
n=7; %número de términos
c_x=sym2poly(taylor(exp(x),'order',n));
cT=zeros(1,n);
for k=1:n
    a=[zeros(1,k-1),potencias_cheby(n-k)];
    cT=cT+c_x(k)*a;
end
%comprobación
Tk=0;
for k=1:n
    Tk=Tk+cT(k)*poly2sym(chebypoly(n-k));
end

>> Tk
Tk =x^6/720 + x^5/120 + x^4/24 + x^3/6 + x^2/2 + x + 1

Una vez que hemos comprobado que el script funciona correctamente con n=7 términos. El desarrollo en serie incluye infinitos términos, n=∞.

>> format long
>> cT
cT =0.000043402777778  0.000520833333333  0.005468750000000  0.044270833333333
0.271484375000000  1.130208333333333  1.266059027777778

Observamos que los primeros coeficientes c₁=0.000043402777778 de T₆, c₂=0.000520833333333 de T₅, c₃=0.005468750000000 de T₄ son próximos a cero, por tanto con n=10 términos podría ser suficiente.

syms x;
n=10; %número de términos
c_x=sym2poly(taylor(exp(x),'order',n));
cT=zeros(1,n);
for k=1:n
    a=[zeros(1,k-1),potencias_cheby(n-k)];
    cT=cT+c_x(k)*a;
end

cT =0.000000010764578  0.000000193762401  0.000003197079613  0.000044952876984
0.000542922247024  0.005474175347222  0.044336841724537  0.271495225694444
1.130318196614583  1.266065809461806

El desarrollo en serie de la función e^x en términos de los polinomios de Chebyshev es

e^x∼1.266066·T₀+1.130318·T₁+0.271495·T₂+0.044337·T₃+0.005474·T₄+0.000543·T₅+...

Aproximación de funciones

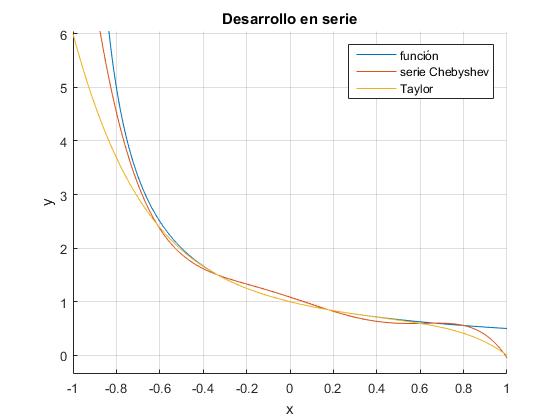
Vamos a aproximar la función e^x con la suma de los tres primeros términos del desarrollo en serie. 1.266066·T₀+1.130318·T₁+0.271495·T₂. Sustituímos T₀ por 1, T₁ por x y T₂ por 2x²-1. Comparamos esta aproximación con el desarrollo en serie de Taylor de tres términos. Elaboramos un script que nos permita aproximar la función e^x a un número m de términos del desarrollo en serie c_nT₀+c_n-1T₁+...c_n-m+1T_m-1 y la vamos a comparar con el mismo número de términos del desarrollo en serie de Taylor. Todas las representaciones gráficas se realizan en el intervalo [-1,1].

syms x;
f=exp(x);
n=10; %número de términos
c_x=sym2poly(taylor(f,'order',n));
cT=zeros(1,n);
for k=1:n
    a=[zeros(1,k-1),potencias_cheby(n-k)];
    cT=cT+c_x(k)*a;
end

Tk=0;
m=3; %tres términos c_8*T_2+c_9*T_1+c_10*T_0
for k=n-m+1:n
    Tk=Tk+cT(k)*poly2sym(chebypoly(n-k));
end
hold on
ezplot(f,[-1,1])
ezplot(Tk,[-1,1])
ezplot(taylor(f,'order',m),[-1,1])
hold off
grid on
legend('función','serie Chebyshev','Taylor','location','northwest')
xlabel('x')
ylabel('y')
title('Desarrollo en serie')

>> vpa(Tk,6)
ans =0.54299*x^2 + 1.13032*x + 0.994571
>> taylor(exp(x),'order',m)
ans =x^2/2 + x + 1

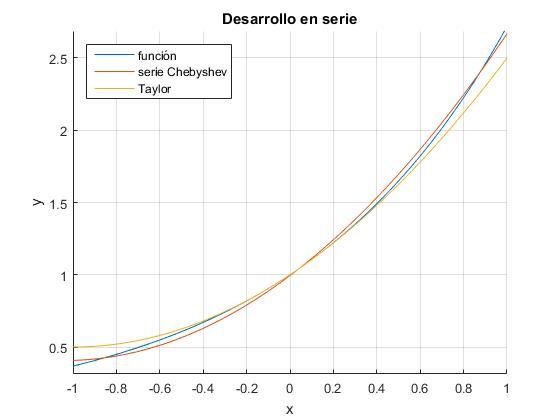
Apreciamos que, la aproximación en términos de los polinomios de Chebyshev se ajusta mucho más a la función e^x. Tomando m=4, no se aprecia apenas diferencia entre la función y dicho desarrollo en serie tal como se ve en la figura más abajo

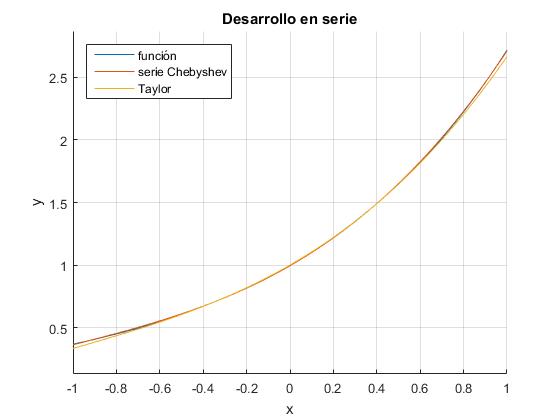
>> vpa(Tk,6)
ans =0.177347*x^3 + 0.54299*x^2 + 0.997308*x + 0.994571
>> taylor(exp(x),'order',m)
ans =x^3/6 + x^2/2 + x + 1

Probamos ahora, la función f(x)=(1+x)^-1, tomando m=6 términos del desarrollo en serie

syms x;
f=(1+x)^-1;
n=10; %número de términos
c_x=sym2poly(taylor(f,'order',n));
cT=zeros(1,n);
for k=1:n
    a=[zeros(1,k-1),potencias_cheby(n-k)];
    cT=cT+c_x(k)*a;
end

Tk=0;
m=6;
for k=n-m+1:n
    Tk=Tk+cT(k)*poly2sym(chebypoly(n-k));
end
hold on
ezplot(f,[-1,1])
ezplot(Tk,[-1,1])
ezplot(taylor(f,'order',m),[-1,1])
hold off
grid on
legend('función','serie Chebyshev','Taylor')
xlabel('x')
ylabel('y')
title('Desarrollo en serie')