Función exponencial y logarítmica

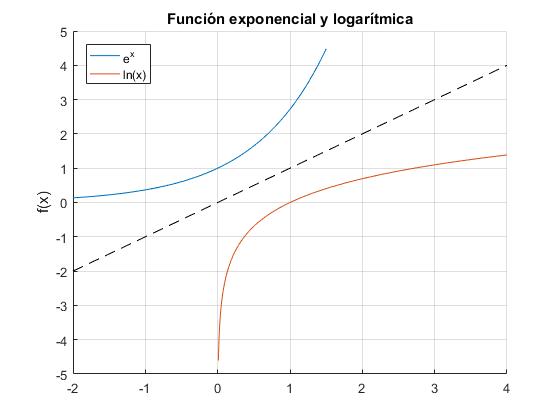
El dominio de la función exponencial e^x es de (-∞, +∞). La función exponencial tiende a cero cuando x tiende a -∞. Para x=0, e^x=1

El dominio de la función inversa ln(x) es (0, +∞). Cuando x tiende a cero ln(x) tiende a -∞.

En la gráfica, vemos la relación de simetría entre la función exponencial y su inversa, la función logarítmica

hold on
fplot(@exp,[-3,1.5])
fplot(@log,[0.01,5])
line([-2,4],[-2,4],'lineStyle','--','color','k')
hold off
grid on
xlim([-2,4])
legend('e^x','ln(x)', 'location', 'northwest')
ylabel('f(x)')
title('Función exponencial y logarítmica')

Funciones trigonométricas

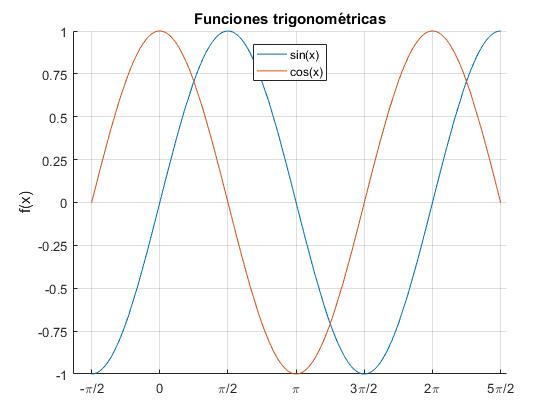
La función seno y coseno son periódicas de periodo 2π
sin(θ+2π)=sin(θ)
cos(θ+2π)=cos(θ)

El seno y coseno son complementarios
sin(π/2-θ)=cos(θ)
cos(π/2-θ)=sin(θ)

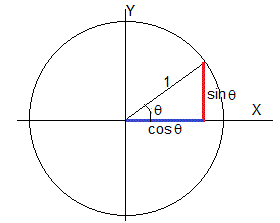
En una circunferencia de radio unidad, las proyección del radio que forma un ángulo θ con el eje X, sobre dicho eje es el coseno del ángulo, y la proyección sobre el eje Y es el seno del ángulo, tal como se muestra en la figura

Por el teorema de Pitágoras

sin²θ+cos²θ=1

La función seno es impar sin(θ)=-sin(-θ) y la función coseno es par, cos(θ)=cos(-θ)

hold on
fplot(@sin,[-pi/2,5*pi/2])
fplot(@cos,[-pi/2,5*pi/2])
hold off
set(gca,'XTick',-pi/2:pi/2:5*pi/2)
set(gca,'XTickLabel',{'-\pi/2','0','\pi/2','\pi','3\pi/2','2\pi','5\pi/2'})
set(gca,'YTick',-1:0.25:1)
 
grid on
legend('sin(x)','cos(x)','location','north')
ylabel('f(x)')
title('Funciones trigonométricas')

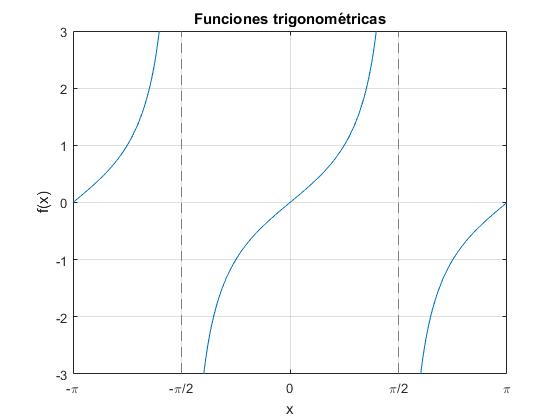
La función tangente tan(x)=sin(x)/cos(x), es periódica de periodo π, tan(θ+π)=tan(θ)

La función tangente tiene asíntotas verticales en π/2, -π/2, 3π/2...

fplot(@tan,[-pi,pi])
set(gca,'XTick',-pi:pi/2:pi)
set(gca,'XTickLabel',{'-\pi','-\pi/2','0','\pi/2','\pi'})
 
grid on
ylim([-3,3])
xlabel('x')
ylabel('f(x)')
title('Funciones trigonométricas')

Algunas relaciones entre las funciones trigonométricas

• sin(A+B)=sinA·cosB+cosA·sinB
• sin(A-B)=sinA·cosB-cosA·sinB
• cos(A+B)=cosA·cosB-sinA·sinB
• cos(A-B)=cosA·cosB+sinA·sinB
• sin(2A)=2sinA·cosA
• cos(2A)=cos²A-sin²A
• sin²A=(1-cos(2A))/2
• cos²A=(1+cos(2A))/2

Funciones inversas

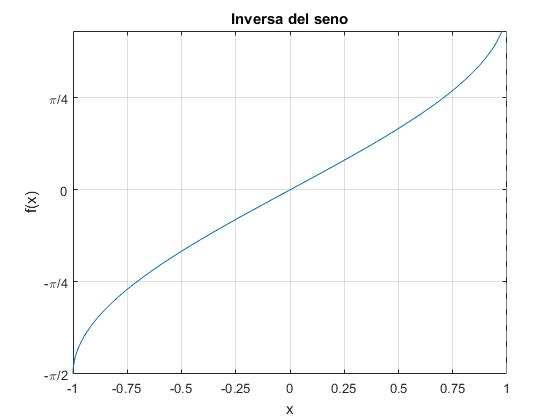
Inversa del seno

Su dominio va de [-1,1],

fplot(@asin,[-1,1])
grid on
xlabel('x')
ylabel('f(x)')
set(gca,'YTick',-pi/2:pi/4:pi/2)
set(gca,'YTickLabel',{'-\pi/2','-\pi/4','0','\pi/4','\pi/2'})
set(gca,'XTick',-1:0.25:1)
title('Inversa del seno')

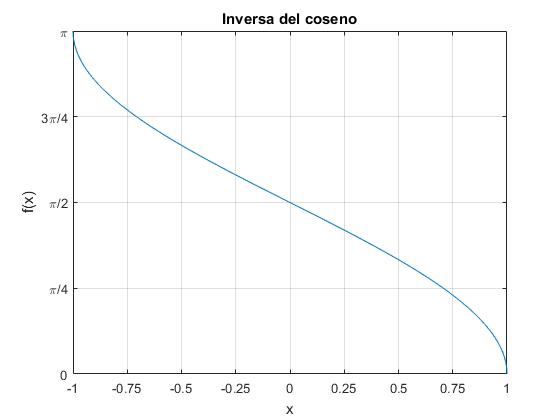
Inversa del coseno

Su dominio va de [-1,1],

fplot(@acos,[-1,1])
grid on
xlabel('x')
ylabel('f(x)')
set(gca,'YTick',0:pi/4:pi)
set(gca,'YTickLabel',{'0','\pi/4','\pi/2','3\pi/4','\pi'})
set(gca,'XTick',-1:0.25:1)
title('Inversa del coseno')

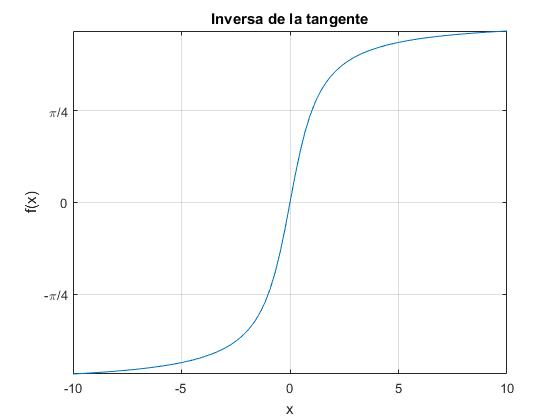
Inversa de la tangente

Su dominio va de (-∞,+∞),

fplot(@atan,[-10,10])
grid on
xlabel('x')
ylabel('f(x)')
set(gca,'YTick',-pi/2:pi/4:pi/2)
set(gca,'YTickLabel',{'-\pi/2','-\pi/4','0','\pi/4','\pi/2'})
set(gca,'XTick',-10:5:10)
title('Inversa de la tangente')

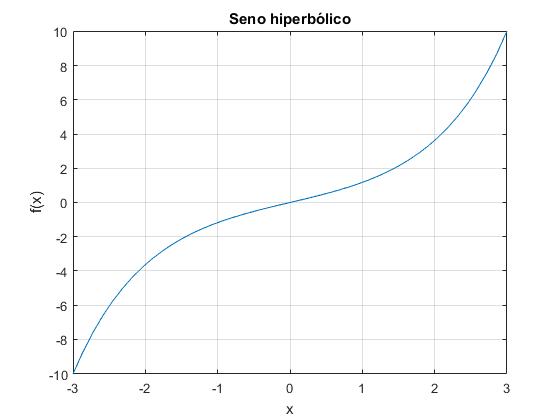
Funciones hiperbólicas

El seno hiperbólico

${\displaystyle \sinh (x)=\frac{e^x-e^{-x}}{2}}$

Es una función impar sinh(-x)=-sinh(x)

fplot(@sinh,[-3,3])
grid on
xlabel('x')
ylabel('f(x)')
title('Seno hiperbólico')

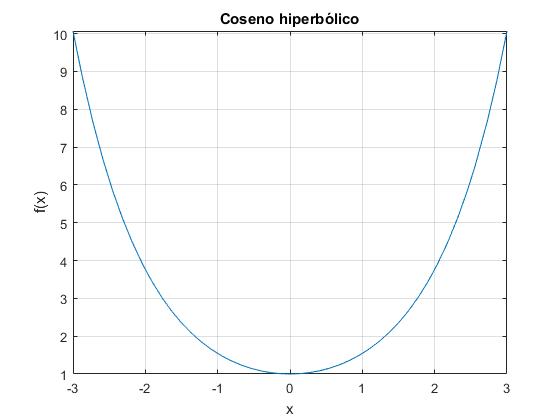
El coseno hiperbólico

${\displaystyle \cosh (x)=\frac{e^x+e^{-x}}{2}}$

Es una función par cosh(-x)=cosh(x)

fplot(@cosh,[-3,3])
grid on
xlabel('x')
ylabel('f(x)')
title('Coseno hiperbólico')

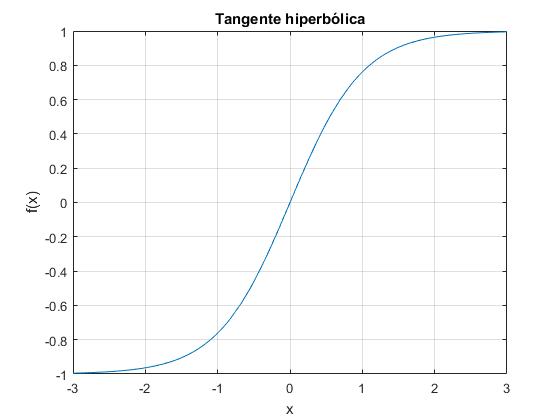
La tangente hiperbólica

${\displaystyle \tanh (x)=\frac{e^x-e^{-x}}{e^x+e^{-x}}}$

La función y=tanh(x), es una función impar que tiene dos asíntotas horizontales cuando x tiende hacia +∞ y tiende a 1, cuando x tiende hacia -∞ y tiende a -1

fplot(@tanh,[-3,3])
grid on
xlabel('x')
ylabel('f(x)')
title('Tangente hiperbólica')

Algunas relaciones entre las funciones hiperbólicas

• cosh²A-sinh²A=1
• sinh(A+B)=sinhA·coshB+coshA·sinhB
• sinh(A-B)=sinhA·coshB-coshA·sinhB
• cosh(A+B)=coshA·coshB+sinhA·sinhB
• cosh(A-B)=coshA·coshB-sinhA·sinhB
• sinh(2A)=2sinhA·coshA
• cosh(2A)=cosh²A+sinh²A
• sinh²A=(cosh(2A)-1)/2
• cosh²A=(1+cosh(2A))/2

Funciones inversas

Inversa del seno hiperbólico

${\displaystyle \begin{array}{l}x=\sinh y\\ x=\frac{e^y-e^{-y}}{2}\\ {\left(e^y\right)}^2-2x{e}^y-1=0\\ e^y=x+\sqrt{1+x^2}\\ y=\ln \left(x+\sqrt{1+x^2}\right)\end{array}}$

Dado que la exponencial es un número positivo solamente hay una raíz de la ecuación de segundo grado

fplot(@asinh,[-10,10])
grid on
xlabel('x')
ylabel('f(x)')
title('Inversa del seno hiperbólico')

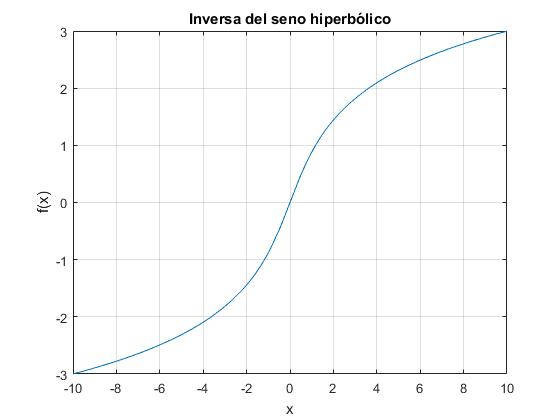
Alternativamente, obtenemos la misma gráfica con el código

f=@(x) log(x+sqrt(1+x.^2));
fplot(f,[-10,10])
grid on
xlabel('x')
ylabel('f(x)')
title('Inversa del seno hiperbólico')

Inversa del coseno hiperbólico

${\displaystyle \begin{array}{l}y={\cosh }^{-1}x\\ x=\cosh y\\ x=\frac{e^y+e^{-y}}{2}\\ {\left(e^y\right)}^2-2x{e}^y+1=0\\ e^y=x+\sqrt{x^2-1}\\ y=\ln \left(x+\sqrt{x^2-1}\right)\end{array}}$

Dado que la exponencial es un número positivo solamente hay una raíz de la ecuación de segundo grado

fplot(@acosh,[1,10])
grid on
xlabel('x')
ylabel('f(x)')
title('Inversa del coseno hiperbólico')

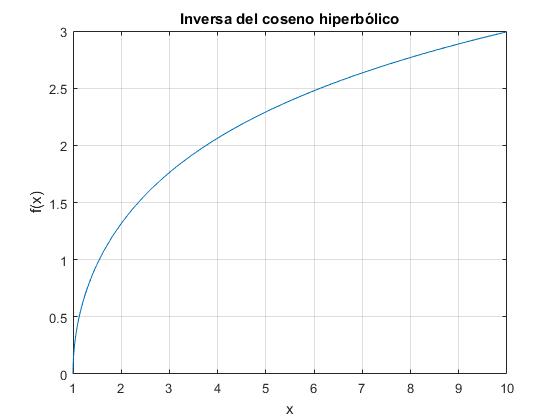
Alternativamente, obtenemos la misma gráfica con el código

f=@(x) log(x+sqrt(x.^2-1));
fplot(f,[1,10])
grid on
xlabel('x')
ylabel('f(x)')
title('Inversa del seno hiperbólico')

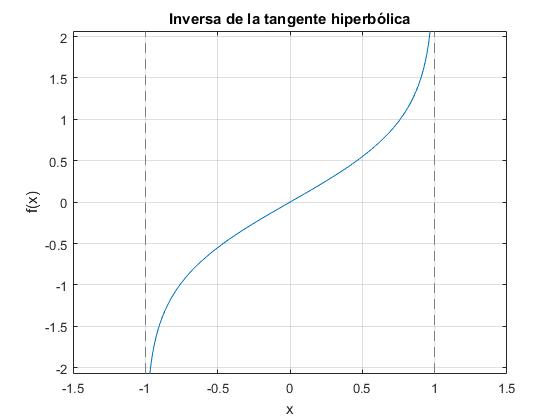
Inversa de la tangente hiperbólica

${\displaystyle \begin{array}{l}y={\tanh }^{-1}x\\ x=\frac{e^y-e^{-y}}{e^y+e^{-y}}\\ {\left(e^y\right)}^2=\frac{1+x}{1-x}\\ y=\frac{1}{2}\ln \left(\frac{1+x}{1-x}\right)\end{array}}$

fplot(@atanh,[-1.5,1.5])
grid on
xlabel('x')
ylabel('f(x)')
title('Inversa de la tangente hiperbólica')

Alternativamente, obtenemos la misma gráfica con el código

f=@(x) log((1+x)./(1-x))/2;
fplot(f,[-1.5,1.5])
grid on
xlabel('x')
ylabel('f(x)')
title('Inversa de la tangente hiperbólica')