Consideremos la función, f(x)=x·e^x

f=@(x) x.*exp(x);
fplot(f,[-4,1])
xlabel('x')
ylabel('y')
axis([-4, 1, -.5, 1])
grid on
line([-1,-1],[-1/exp(1),-1/exp(1)],'marker','.','markersize',15,'color','k')
set(gca,'yTick',[-1/exp(1),0,0.5,1])
set(gca,'yTickLabel',{'-1/e','0','0.5','1'})

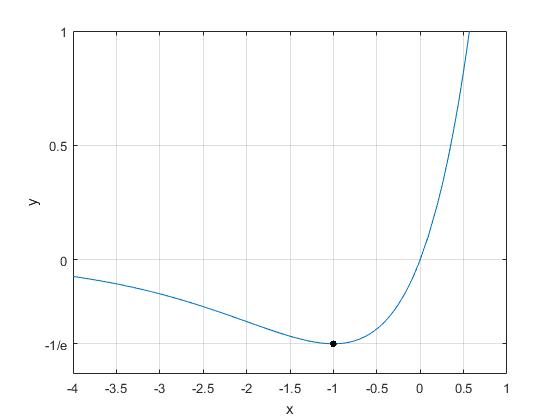
La función f(x) tiene un mínimo en x=-1, y el valor de este mínimo es -1/e juega un papel importante en la definición de la función W de Lambert.

La función W de Lambert

La función W de Lambert, W(x) es la inversa de la función f(x).

${\displaystyle W(x)·e^{W(x)}=x}$

Se representa gráficamente, intercambiando los ejes horizontal y vertical mediante el comando view.

f=@(x) x.*exp(x);
hold on
fplot(f,[-4 -1])
fplot(f,[-1,1])
hold off
xlabel('y')
ylabel('x')
axis([-4 1 -.5 1])
view([90,-90])
grid on
line([-1,-1],[-1/exp(1),-1/exp(1)],'marker','.','markersize',15,'color','k')
set(gca,'ytick',[-1/exp(1),0,0.5,1])
set(gca,'yticklabel',{'-1/e','0','0.5','1'})

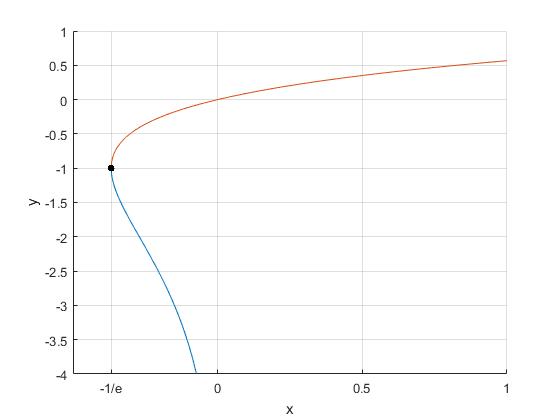
La función W(x) está definida en el intervalo [-1/e, ∞), con dos ramas:

• En color rosa W(x)≥-1, la rama W₀(x) es una función creciente en el intervalo [-1/e, ∞)
• En color azul W(x)<-1, la rama W_-1(x) es una función decreciente en el intervalo (-1/e, 0)

La función W(x) tiene un valor en el intervalo [0,∞) y dos valores en el intervalo [-1/e,0)

Valores significativos de W(x)

Como vemos en la gráfica, W(0)=0 y W(-1/e)=-1. Existen otros valores significativos derivados de que W(x) es la función inversa de f(x)=x·e^x.

En la primera gráfica, al valor de abscisa 2 le corresponde 2·e² en la ordenada. Luego, en la función inversa, a la abscisa x=2e² la corresponde la ordenada W(2e²)=2. En general, W(x·e^x)=x. Valores importantes son

• x=1, W(1·e¹)=1 o bien, W(e)=1

• x=-1, W(-1·e^-1)=-1, o bien, W(-1/e)=-1 que ya hemos mencionado y señalado en la gráfica mediante un punto de color negro

Otros valores de de W(x)

Otros valores de W(x) hay que calcularlos de forma numérica, mediante el procedimiento de Newton u otros procedimientos que convergen más rápidamente como el de Halley.

El cálculo deW(x) para un valor dado de x requiere resolver la ecuación transcendente, f(w)=we^w-x=0.

El procedimiento de Newton calcula la raíz de la ecuación mediante un proceso iterativo de la siguiente forma

${\displaystyle w_{n+1}=w_n-\frac{f(w_n)}{f\text{'}(w_n)}}$

f'(w) es la derivada de f(w) respecto de w. f'(w)=e^w+w·e^w=(1+w)e^w.

El procedimiento de Newton precisa un valor de partida w₀ en el proceso de iteracción:

• Para x≥0, hay una única solución, el valor de partida aconsejable es w₀=1
• Para -1/e≤x<0, hay dos posibles soluciones, para la rama W₀(x) se elige el valor de partida w₀=1, para la rama W_-1(x) se elige el valor de partida w₀=-2

x=1;
f=@(w) w*exp(w)-x; %función
f_prima=@(w) (w+1)*exp(w); %derivada
w0=1; %valor inicial
while(1)
        w=w0-f(w0)/f_prima(w0);
        if abs((w-w0)/w)<1e-5 
            break
        end
        w0=w;
    end
disp([x,w]);

Corremos el script y en la ventana de comandos, aparece el valor W(1)=0.5671

>>   0.5671

Creamos una función denominada lambert_newton, tal que dado el valor de x y la rama 0 ó, -1, correspondientes a las funciones W₀(x) o W_-1(x), devuelve el valor de w.

function w =lambert_newton(rama,x)
    if (rama==0)
        w0=1;
    else
        w0=-2;
    end
    while(1)
        w=w0-(w0*exp(w0)-x)/((w0+1)*exp(w0));
        if abs((w-w0)/w)<1e-5 
            break
        end
        w0=w;
    end
end

Llamamos a la función lambert_newton para obtener una tabla de valores, x, W(x). Tomamos valores de x comprendidos entre -1/e e ∞ y calculamos el valor correspondiente a la primera rama W₀(x)

x1=[2*exp(2),exp(1),2,1,1/exp(1),-1/4,-2/exp(1)^2,-1/exp(1)];
for x=x1
    w=lambert_newton(0,x);
    disp([x,w])
end

   14.7781    2.0000
    2.7183    1.0000
    2.0000    0.8526
    1.0000    0.5671
    0.3679    0.2785
   -0.2500   -0.3574
   -0.2707   -0.4064
   -0.3679   -1.0000

Llamamos a la función lambert_newton para obtener una tabla de valores, x, W(x). Tomamos valores de x comprendidos entre -1/e y cero y calculamos el valor correspondiente a la segunda rama W_-1(x)

x2=[-1/4,-2/exp(1)^2,-1/exp(1)];
for x=x2
    w=lambert_newton(-1,x);
    disp([x,w])
end

   -0.2500   -2.1533
   -0.2707   -2.0000
   -0.3679   -1.0000

En vez de utilizar la función propia, lambert_newton prodríamos haber utilizado la función lambertw de MATLAB, para obtener los mismos resultados. Ahora la utilizaremos para representar gráficamente la función W(x)

hold on
x=-1/exp(1):0.01:1;
plot(x,lambertw(0,x))

x=-1/exp(1):0.01:0;
plot(x,lambertw(-1,x))
hold off

axis([-.5, 1, -4, 1])
line([-1/exp(1), -1/exp(1)],[-1, -1],'marker','.','markersize',18,'color','black')
set(gca,'xtick',[-1/exp(1), 0, 0.5, 1])
set(gca,'xticklabel',{'-1/e','0','0.5','1'})
set(gca,'ytick',-4:1)
grid on
xlabel('x')
ylabel('w')
title('Lambert W')
legend({'W_0','W_{-1}'},'location','southeast')

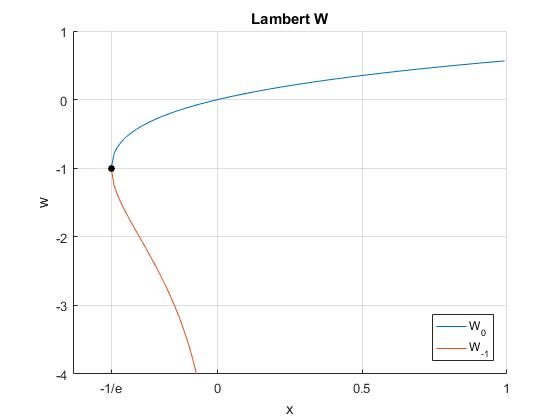
Ecuaciones transcendentes

Muchas ecuaciones que contienen exponenciales se pueden resolver en términos de la función W Lambert, agrupando los términos de la forma f(x)·exp(f(x)).

Ecuación x+e^x=0

Multiplicamos los dos miembros de la ecuación -x=e^x por e^-x

-x·e^-x=1

La solución exacta es -x=W₀(1).

>> -lambertw(0,1)
ans =   -0.5671

Ecuación, x^x=8

Resolvemos esta ecuación siguiendo los pasos

${\displaystyle \begin{array}{l}{x}^x=8\\ x\ln x=\ln 8\\ \ln x·e^{\ln x}=\ln 8\\ z·e^z=\ln 8\end{array}}$

Como ln8>0 solamente hay una solución

${\displaystyle \begin{array}{l}z=W_0\left(\ln 8\right)\\ x=\exp \left(W_0\left(\ln 8\right)\right)\end{array}}$

>> exp(lambertw(0,log(8)))
ans =    2.3884

La ley del desplazamiento de Wien

En la página titulada El cuerpo negro, calculamos el máximo de la función de la distribución de Planck expresada en términos de la longitud de onda, la denominada ley de desplazamiento de Wien

${\displaystyle 5(e^x-1)-x{e}^x=0x=\frac{hc}{\lambda kT}}$

Una solución de esta ecuación es x=0. Buscamos otras soluciones de esta ecuación transcendente

${\displaystyle \begin{array}{l}(x-5)e^x=-5\\ (x-5)e^{(x-5)}=-5e^{-5}\\ z{e}^z=-5e^{-5}\\ z=W_0\left(-5e^{-5}\right)\\ x=5+W_0\left(-5e^{-5}\right)\end{array}}$

Como -5e^-5=-0.034 está en el intervalo que va desde -1/e=-0.3679 a cero, hay dos posibles soluciones

>> 5+lambertw(-1,-5*exp(-5))
ans =     0
>> 5+lambertw(0,-5*exp(-5))
ans =    4.9651

Se obtuvo este valor utilizando procedimientos numéricos

Ecuación x²=2^x

Representamos las dos funciones y=x², e y=2^x

f=@(x) x.^2;
g=@(x) 2.^x;
hold on
fplot(f,[-2,5])
fplot(g,[-2,5]),
hold off
grid on
axis([-2,5,-0.5,20])
xlabel('x')
ylabel('y')
title('Ecuación 2^x=x^2')

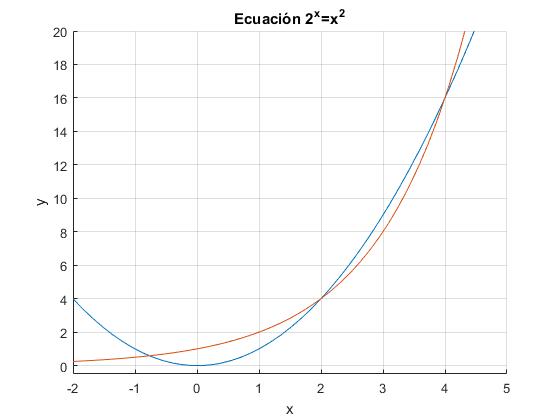
Vemos que hay tres puntos de intersección, x=2, x=4 y otro próximo a x=-1.

Hallando la raíz cuadrada

${\displaystyle \begin{array}{l}{x}^2=2^x\\ x=\pm 2^{x/2}\end{array}}$

Tomamos la raíz positiva para calcular las abscisas de los dos primeros puntos de intersección, siguiendo los pasos

${\displaystyle \begin{array}{l}\ln x=\frac{x\ln 2}{2}\\ x=\exp \left(\frac{x\ln 2}{2}\right)\\ x·\exp \left(\frac{-x\ln 2}{2}\right)=1\\ \frac{-x\ln 2}{2}\exp \left(\frac{-x\ln 2}{2}\right)=-\frac{\ln 2}{2}\\ z·\exp (z)=-\frac{\ln 2}{2}\end{array}}$

Como -ln2/2=-0.3466, está en el intervalo que va desde -1/e=-0.3679 a cero, hay dos posibles soluciones.

${\displaystyle \begin{array}{l}{z}_1=W_0\left(-\frac{\ln 2}{2}\right)\\ z_2=W_{-1}\left(-\frac{\ln 2}{2}\right)\\ x_1=-\frac{2}{\ln 2}{W}_0\left(-\frac{\ln 2}{2}\right)=2\\ x_2=-\frac{2}{\ln 2}{W}_{-1}\left(-\frac{\ln 2}{2}\right)=4\end{array}}$

Calculamos ahora la abscisa del tercer punto de intersección, para el caso negativo

${\displaystyle \begin{array}{l}-x=2^{x/2}\\ \ln (-x)=\frac{x\ln 2}{2}\\ -x=\exp \left(\frac{x\ln 2}{2}\right)\\ -x·\exp \left(\frac{-x\ln 2}{2}\right)=1\\ \frac{-x\ln 2}{2}\exp \left(\frac{-x\ln 2}{2}\right)=\frac{\ln 2}{2}\\ z·\exp (z)=\frac{\ln 2}{2}\end{array}}$

Como ln2/2=0.3466, es mayor que cero, solamente es posible una solución.

${\displaystyle \begin{array}{l}{z}_3=W_0\left(\frac{\ln 2}{2}\right)\\ x_3=-\frac{2}{\ln 2}{W}_0\left(\frac{\ln 2}{2}\right)=-0.7667\end{array}}$

Así pues, las raíces exactas de la ecuación x²-2^x=0, son, 2, 4 y

${\displaystyle -\frac{2}{\ln 2}{W}_0\left(\frac{\ln 2}{2}\right)}$

>> -2*lambertw(0, -log(2)/2)/log(2)
ans =    2.0000
>> -2*lambertw(-1, -log(2)/2)/log(2)
ans =    4.0000
>> -2*lambertw(0,log(2)/2)/log(2)
ans =   -0.7667

Ecuación a^b·x+c=d·x+f

Consideremos en general, la ecuación a^b·x+c=d·x+f con a>0, b≠0, d≠0

Efectuamos el cambio de variable, -t=b·x+b·f/d y seguimos los pasos

${\displaystyle \begin{array}{l}bx=-t-\frac{bf}{d}\\ dx+f=d\left(\frac{-t-\frac{bf}{d}}{b}\right)+f=-\frac{td}{b}\\ a^{bx+c}=dx+f\\ a^{-t}{a}^{c-bf/d}=-\frac{td}{b}\\ \frac{-b}{d}{a}^{c-bf/d}=t{a}^t\\ \frac{-b}{d}{a}^{c-bf/d}=t{e}^{t\ln a}\end{array}}$

Multiplicando ambos miembros por lna

${\displaystyle \frac{-b}{d}\left(\ln a\right)a^{c-bf/d}=t\left(\ln a\right)e^{t\ln a}}$

Para conseguir la forma u=w·exp(w) ó w=W(u)

${\displaystyle t\ln a=W\left(\frac{-b}{d}\left(\ln a\right)a^{c-bf/d}\right)}$

Deshaciendo el cambio de variable

${\displaystyle x=\frac{-1}{b\ln a}W\left(\frac{-b}{d}\left(\ln a\right)a^{c-bf/d}\right)-\frac{f}{d}}$

Ejemplo: Sea la ecuación 2^x=10x

a=2, b=1, c=0, d=10, f=0.

La solución exacta es

${\displaystyle x=\frac{-1}{\ln 2}W\left(\frac{-\ln 2}{10}\right)}$

Como ln2/10=-0.069 está comprendido entre -1/e y 0, hay dos posibles soluciones, tal como puede verse en la figura

f=@(x) 10*x;
g=@(x) 2.^x;
hold on
fplot(f,[0,6])
fplot(g,[0,6]),
hold off
grid on
xlabel('x')
ylabel('y')
title('Ecuación 2^x=10x')

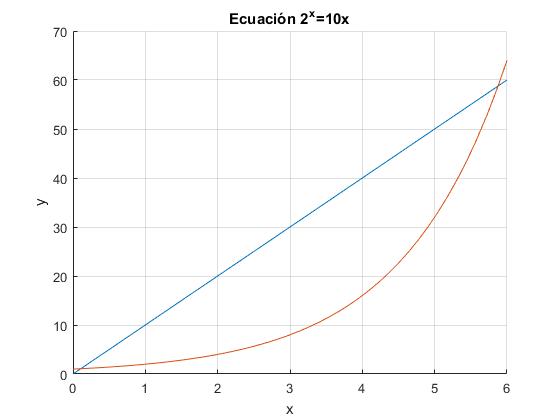
>> -lambertw(0,-log(2)/10)/log(2
ans =    0.1078
>> -lambertw(-1,-log(2)/10)/log(2)
ans =    5.8770

Ecuación Q=ax^mexp(-bxⁿ)

Vamos a resolver la ecuación

${\displaystyle Q=a{x}^m\exp \left(-b{x}^n\right)}$

• Q es una constante o una función de x
• a y b son constantes o funciones que no dependen de x pero pueden depender de otros parámetros
• Los exponentes m y n pueden ser números positivos o negativos, no nulos, enteros o números racionales.

Un ejemplo ilustrativo es la ecuación de Richardson que describe la emisión termoiónica.

${\displaystyle J=A{T}^2\exp \left(-\frac{\phi }{k_{B}T}\right)}$

donde a=A, x=T, m=2, n=-1, b=φ/k_B

Expresamos la ecuación de la forma u=w·exp(w) ó w=W(u)

${\displaystyle \begin{array}{l}\frac{Q}{a}=x^m\exp \left(-b{x}^n\right)\\ {\left(\frac{Q}{a}\right)}^{\frac{n}{m}}={\left(x^m\exp \left(-b{x}^n\right)\right)}^{\frac{n}{m}}\\ {\left(\frac{Q}{a}\right)}^{\frac{n}{m}}=x^n\exp \left(-b\frac{n}{m}{x}^n\right)\\ -\frac{n}{m}b{\left(\frac{Q}{a}\right)}^{\frac{n}{m}}=-\frac{n}{m}b{x}^n\exp \left(-b\frac{n}{m}{x}^n\right)\end{array}}$

Despejamos la incógnita x

${\displaystyle \begin{array}{l}-b\frac{n}{m}{x}^n=W\left(-\frac{n}{m}b{\left(\frac{Q}{a}\right)}^{\frac{n}{m}}\right)\\ x={\left(-\frac{m}{n}\frac{1}{b}W\left(-\frac{n}{m}b{\left(\frac{Q}{a}\right)}^{\frac{n}{m}}\right)\right)}^{\frac{1}{n}}\end{array}}$

Medida de la constante de Boltzmann mediante el efecto Hall

El punto de partida es la concentración n_p de portadores de carga en un semiconductor a la temperatura T

${\displaystyle n_p=2{\left(\frac{k_{B}T}{2\pi {\hslash }^2}\right)}^{\frac{3}{2}}{\left(m_e{m}_h\right)}^{\frac{3}{4}}\exp \left(-\frac{E_g}{2k_{B}T}\right)}$

• m_e y m_h son las masas efectivas de los electrones y los huecos.
• E_g es el intervalo de energía que separa la banda de conducción y de la de valencia
• k_B es la constante de Boltzmann

${\displaystyle \begin{array}{l}a{x}^{\frac{3}{2}}\exp \left(-b{x}^{-1}\right)=Q,\{\begin{array}{l}x=k_B\\ a=2{\left(\frac{T\sqrt{m_e{m}_h}}{2\pi {\hslash }^2}\right)}^{\frac{3}{2}}\\ b=\frac{1}{2}\frac{E_g}{T}\end{array}\{\begin{array}{l}m=\frac{3}{2}\\ n=-1\\ Q=n_p\end{array}\\ x={\left(\frac{3}{2}\frac{1}{b}W\left(\frac{2}{3}b{\left(\frac{Q}{a}\right)}^{-\frac{2}{3}}\right)\right)}^{-1}=\frac{2b}{3}\frac{1}{W\left(\frac{2}{3}b{\left(\frac{a}{Q}\right)}^{\frac{2}{3}}\right)}\end{array}}$

La incógnita k_B es

${\displaystyle k_B=\frac{E_g}{3T}\frac{1}{W\left(\frac{1}{3·2^{\frac{1}{3}}\pi }\frac{\sqrt{m_e{m}_h}}{{\hslash }^2}\frac{E_g}{n^{\frac{2}{3}}}\right)}}$

Ejemplos en el Curso Interactivo de Física

La descarga de un depósito de líquido a través de un tubo capilar

Fuerza de rozamiento proporcional a la velocidad

Fuerza de rozamiento proporcional al cuadrado de la velocidad

Medida de la viscosidad de un líquido mediante dos vasos comunicantes (II)

Propulsión a chorro

Fenómenos capilares

El potencial delta de Dirac, E<0

Referencias

Seán Stewart. A new elementary function for our curricula?. The Petroleum Institute, United Arab Emirates. Australian Senior mathematics 19(2)

Thomas P. Dence. A Brief Look into the Lambert W Function Applied Mathematics, 2013, 4, 887-892.

Edward W. Packel, David S. Yuen. Projectile Motion with Resistance and the Lambert W Function. VOL. 35, NO. 5, NOVEMBER 2004 THE COLLEGE MATHEMATICS JOURNAL

Ahmed Houari. New analytical results in solid state physics using the Lambert W function. Eur. J. Phys. 44 (2023) 065502